用于變形監(jiān)測的最小二乘濾波數據處理

李偉東，林 楠,2，劉德利，孫曉磊

1.吉林建筑大學測繪與勘查工程學院，長春 130118 2.吉林大學地球探測科學與技術學院，長春 130026

用于變形監(jiān)測的最小二乘濾波數據處理

李偉東1，林 楠1,2，劉德利1，孫曉磊1

1.吉林建筑大學測繪與勘查工程學院，長春 130118 2.吉林大學地球探測科學與技術學院，長春 130026

隨著全站儀在測量工作中的廣泛使用，以坐標為觀測值的數據處理成為內業(yè)工作的主要內容。根據最小二乘濾波原理，將工程巖土體變形監(jiān)測中所獲得的坐標觀測值及其他常規(guī)觀測值進行聯合平差。結果表明，濾波后變形點的點位精度最大可提高1.35 mm，最弱點亦提高0.94 mm，均明顯高于直接觀測結果，而且各類觀測值之間所形成的約束條件進一步增強了平差結果的可靠性。

最小二乘；濾波；變形監(jiān)測；坐標觀測值

0 引言

隨著全站儀在測量工作中的廣泛使用，以點的坐標為觀測值的量測方法逐漸成為測量數據獲取的主要形式[1-4]。但是，由于坐標觀測值本身的特性，與常規(guī)的邊長、角度等觀測值相比較，空間點與點之間的關系不再具備明顯的聯系，導致坐標觀測值缺乏幾何上的多余觀測，因而無法用經典平差理論進行相應的數據處理。最小二乘濾波是將平差過程中的全部待估參數均視為隨機參數，在已知其先驗統(tǒng)計信息的前提下，按照廣義最小二乘原理求定參數最佳估值的一種方法。由于其良好的運算性能，該方法近年來已經成為眾多學者研究的熱點[5-13]。

筆者基于最小二乘濾波原理，提出一種新的變形監(jiān)測數據處理方法：在全站儀對變形點坐標進行觀測的同時，輔之以相應數量的高差、邊長或角度等常規(guī)觀測值；進而選擇變形點坐標為隨機參數，實現對坐標值的最優(yōu)估計。由于這種方法可以形成幾何條件與觀測數量上的多余觀測，故對于提高平差結果的精度和可靠性將會產生明顯的效果。

1 最小二乘濾波原理

由廣義測量平差原理可知，設L為正態(tài)隨機觀測向量，X為系統(tǒng)狀態(tài)參數(或稱信號，服從正態(tài)分布)向量。參數X和觀測值L具有以下先驗統(tǒng)計性質[14-17]：

式中：μx、μL分別代表系統(tǒng)狀態(tài)參數和觀測向量的驗前期望；DXX、DLL則表示系統(tǒng)狀態(tài)參數和觀測向量的驗前方差矩陣。L和X之間的觀測方程滿足

式中：B為觀測值系數矩陣；Φ為隨機誤差。且隨機誤差與未知參數之間的協(xié)方差為

現用LX表示X的先驗期望μx，即將其視為虛擬觀測值、將待求參數X看作是非隨機的參數，設它所對應的隨機誤差為ΦX，此時，三者之間有觀測方程：

式中：V和VX分別對應著實際觀測值L和虛擬觀測值LX的改正數。

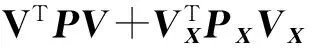
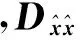
2 坐標與其他常規(guī)觀測值的聯合濾波

利用全站儀測得變形點坐標，同時測出工作基點至變形點之間的距離、角度、高差等常規(guī)觀測值后，就可以按照最小二乘濾波原理，對所有觀測值進行聯合平差[18-21]。

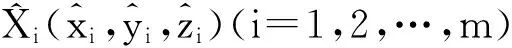
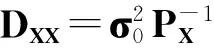
相應的誤差方程為

式中，lX=LX-X0。

其次，由常規(guī)測量觀測值L及待求參數，可建立誤差方程：

式中，l=L-BX0。

將式(8)與式(9)合并，按照廣義最小二乘準則，可求得參數改正數：

通過式(7)可計算相應的參數最或是值。此外，除用式(6)計算參數最或是值協(xié)方差外，還可由(2)式及協(xié)因數傳播律，得到

3 算例

圖1為某醫(yī)院建筑基坑變形監(jiān)測的工作基點與變形點(部分)布置情況示意圖。全站儀標稱測角精度為2.0″、測距精度為2+2×10-6D(D為對應的觀測距離，單位為mm)。以工作基點A(3 020.076,1 096.053 9)為測站，另一基點B(3 001.030 6,1 094.342 9)為后視，測得變形點坐標值見表1。同時以B點為測站，獨立觀測各變形點間的夾角及測站至變形點間的水平距離(表2)。

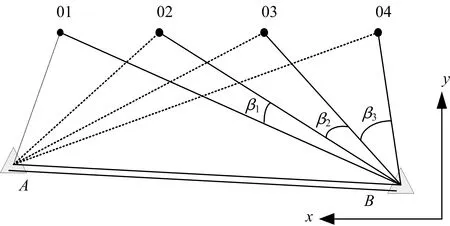
圖1 變形監(jiān)測示意圖Fig. 1 Schematic diagram of deformation monitoring

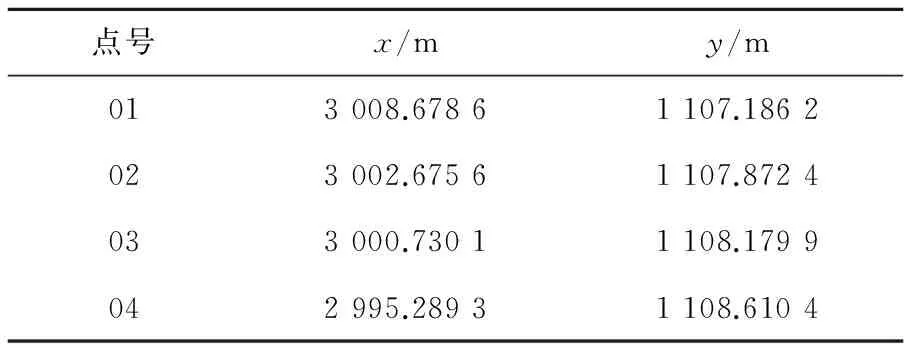
點號x/my/m013008.67861107.1862023002.67561107.8724033000.73011108.1799042995.28931108.6104

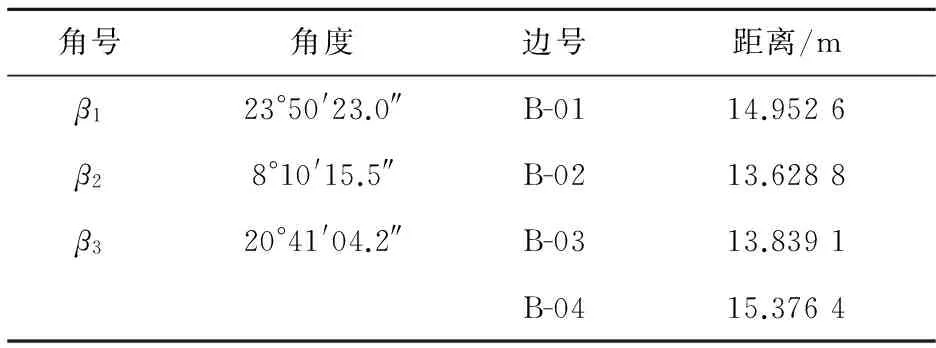
表2 角度、距離觀測值

按照上述最小二乘濾波公式(6)，對測得的觀測值進行平差，得到變形點坐標最或是值(表3)。

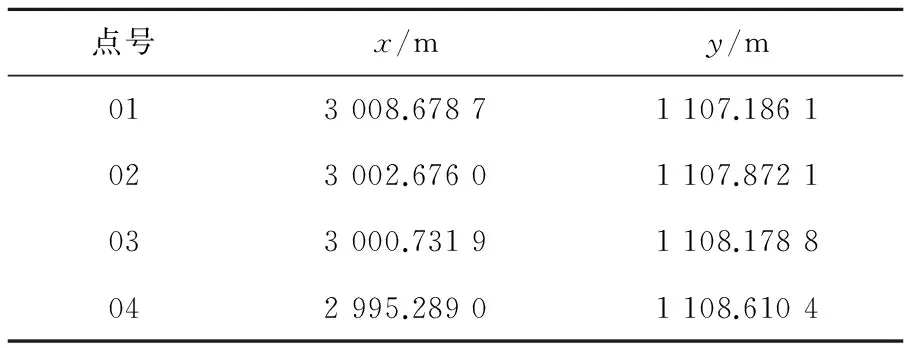
表3 變形點坐標平差值

為檢驗這種方法的實際效果，利用標稱精度更高的Leica TM30儀器(測角精度0.5″，測距精度為0.6+10-6D)進行了同步觀測，并將觀測結果近似為變形點坐標的真值，如表4所示。

表4 變形點高精度坐標觀測值

Table 4 High-precision coordinate value of deformation points

點號x/my/m013008.67981107.1858023002.67661107.8724033000.73261108.1790042995.29001108.6112

對比表1、表3和表4的結果可以明顯看出，經過最小二乘濾波的變形點坐標值更接近TM30的觀測數據。如果將表4的觀測結果作為真值參照，經過最小二乘濾波后的坐標平差值(表3)好于直接觀測結果(表1)。

由全站儀的儀器標稱精度及坐標計算公式，依據協(xié)因數傳播律，在不考慮工作基點點位誤差的前提下，可計算得到各坐標觀測值的驗前協(xié)因數陣；進一步地，根據式(11)，則可計算出坐標平差值的協(xié)因數。表5給出了變形點坐標的驗前和平差后的協(xié)因數對比。

表5 變形點坐標濾波前后協(xié)因數情況

Table 5 Differences of deformation coordinated factor before and after filtering

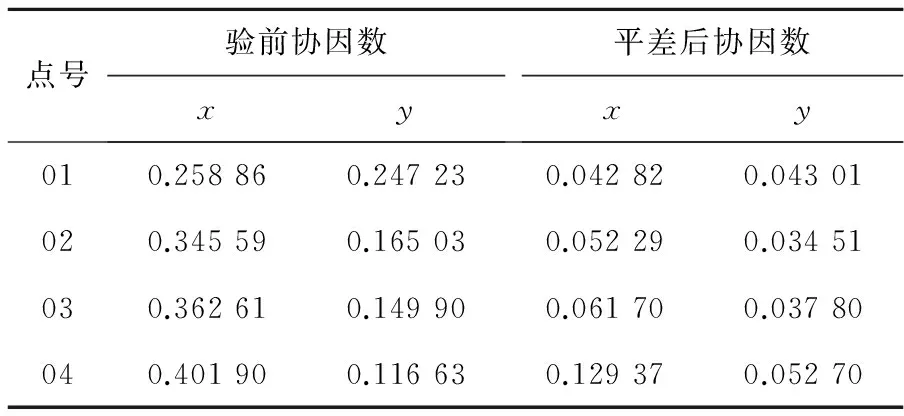
點號驗前協(xié)因數xy平差后協(xié)因數xy010.258860.247230.042820.04301020.345590.165030.052290.03451030.362610.149900.061700.03780040.401900.116630.129370.05270

通過坐標點驗前和平差后的協(xié)因數對比可以明顯看出：平差后的坐標協(xié)因數結果明顯優(yōu)于其先驗值。

平差質量的改善還可以通過精度對比加以體現。根據觀測值平差改正數可得單位權中誤差：

式中：r為多余觀測數。根據表5的坐標協(xié)因數評定結果和式(13)，可計算得到各點的點位精度。表6給出了平差前后變形點位精度的對比。

表6 變形點濾波前后精度對比情況

Table 6 Differences of accuracy of point deformation before and after filtering

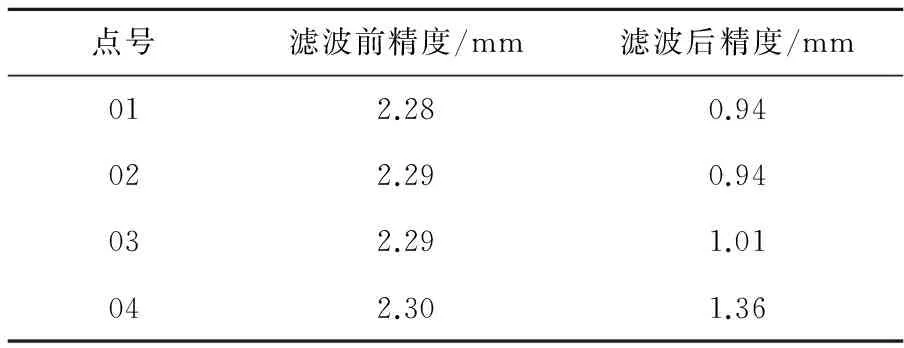
點號濾波前精度/mm濾波后精度/mm012.280.94022.290.94032.291.01042.301.36

通過表6可以明顯看出：由于角度、距離等常規(guī)觀測值的引入，使濾波后變形點的點位精度得到明顯提高。其中，提高幅度最大的點達到1.36 mm，最小的點亦達到0.94 mm。同時，因一定數量的常規(guī)觀測值參與濾波后，使各類觀測值之間形成幾何約束，進一步增強了平差結果的可靠性。

4 結論與建議

隨著全站儀在測量工作中的普遍使用，以坐標為觀測值的數據采集與處理逐漸成為測量內業(yè)的主要內容。在變形監(jiān)測中采用最小二乘濾波進行數據處理，將坐標觀測值視為具有先驗統(tǒng)計信息的隨機參數，與邊長、角度等常規(guī)觀測值進行整體解求，不僅能通過增加多余觀測而提高待定點的精度，還可以利用常規(guī)觀測值與坐標參數之間所形成的約束條件提高待定點坐標最或是值的可靠性，從而在實際應用中會收到很好的效果。同時，由于該方法不僅考慮到待估隨機參數的先驗統(tǒng)計特性，而且數據處理過程仍然采用最小二乘估計準則，故與經典測量平差方法相比較，其數據處理過程較為相似，公式內容也比較容易理解，對于類似的工程應用和數據處理，具有較高的借鑒意義和應用價值，適于在相近的測量工作中推廣。

[1] 李宏男，伊廷華，伊曉東，等.采用GPS與全站儀對大跨斜拉橋進行變形監(jiān)測[J].防災減災工程學報, 2005, 25(1):8-13. Li Hongnan, Yi Tinghua, Yi Xiaodong, et al. Integration of GPS and Total Station Technology for Deformation Monitoring of Long-Span Bridge[J]. Journal of Disaster Prevention and Mitigation Engineering, 2005, 25(1):8-13.

[2] 陳子進，吳斌，梅連友. 全站儀坐標差分法在高邊坡變形監(jiān)測中的應用[J].重慶建筑大學學報, 2005, 27(3):130-135. Chen Zijin, Wu Bin, Mei Lianyou. Application of Coordnate Difference Method in Safe Monitor of High Slope with Total Station Actively[J]. Journal of Chongqing Jianzhu University, 2005, 27(3):130-135.

[3] 高俊強，陶建岳. 利用免棱鏡全站儀進行地鐵隧道斷面測量與計算[J].測繪通報,2005 (10):41-43. Gao Junqiang, Tao Jianyue. Profile Survey and Computation of the Subway Tunnel Using Total-Sation Instrument Without Prism[J]. Bulletin of Surveying and Mapping, 2005(10): 41-43.

[4] 張偉，李會青，洪樹生. 全站儀非固定站差分法監(jiān)測深基坑坑壁位移[J].測繪通報, 2002(10):45-48. Zhang Wei, Li Huiqing, Hong Shusheng. Application of Difference-Method to Safe Monitoring of Deep Pit Setting with Total Station Actively[J]. Bulletin of Surveying and Mapping, 2002(10):45-48.

[5] Wu Yun, Guo Jiming. Single Point Positioning with Sequential Least-Squares Filter and Estimated Real-Time Stochastic Model[J]. Geo-Spatial Information Science, 2002, 11(1):13-16.

[6] 李金剛，趙勇，郭戈，等.最小二乘濾波在某型火控系統(tǒng)信息處理中的應用[J].指揮控制與仿真, 2006, 28(3): 76-79. Li Jingang, Zhao Yong, Guo Ge, et al. Application of Least Squares Filtering in the Information Processing in Fire Control System[J]. Command Control & Simulation, 2006, 28(3): 76-79.

[7] 柴洪洲，崔岳，明鋒. 最小二乘配置方法確定中國大陸主要塊體運動模型[J].測繪學報, 2009, 38(1):61-65. Chai Hongzhou, Cui Yue, Ming Feng. The Determination of Chinese Mainland Crustal Movement Model Using Least-Squares Collocation[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(1): 61-65.

[8] 姚宜斌，陶本藻. 基于最小二乘配置的GPS網平差模型及其應用[J].測繪學院學報, 2003, 20(1):4-6. Yao Yibin, Tao Benzao. The Adjustment Model of GPS Network with Least Squares Collocation[J]. Journal of Institute of Surveying and Mapping, 2003, 20(1): 4-6.

[9] 鄒賢才，李建成. 最小二乘配置方法確定局部大地水準面的研究[J].武漢大學學報：信息科學版, 2004, 29(3): 4-6. Zou Xiancai, Li Jiancheng. A Local Geoid Determination Using Least-Squares Collocation[J]. Geomatics and Information Science of Wuhan University, 2004, 29(3): 4-6.

[10] 藍悅明，陶本藻. 數字化曲線的最小二乘配置[J].測繪通報, 2004(5):1-3. Lan Yueming, Tao Benzao. Least Squares Collocation of Digitized Curve[J]. Bulletin of Surveying and Mapping, 2004(5): 1-3.

[11] 李成仁，岳東杰，丁旭，等.最小二乘配置及多面函數法在高程異常推估中的應用比較[J].勘察科學技術, 2013(3):40-42. Li Chengren, Yue Dongjie, Ding Xu, et al. Application and Comparison of Least Squares Collocation and Multi-Surface Functions Method in Height Anomaly Estimation[J]. Site Investigation Science and Technology, 2013(3):40-42.

[12] 姚道榮，鐘波，汪海洪，等.最小二乘配置與普通Kriging法的比較[J].大地測量與地球動力學, 2008, 28(3): 77-82. Yao Daorong, Zhong Bo, Wang Haihong, et al. Comparison Between Least Square Collocation and Ordinary Kriging[J]. Journal of Geodesy and Geodynamics, 2008, 28(3): 77-82.

[13] 黃建平，薛志廣，步長城，等.基于裂步DSR的最小二乘偏移方法[J].吉林大學學報：地球科學版, 2014, 44(1): 369-374. Huang Jianping, Xue Zhiguang, Bu Changcheng, et al. The Study of Least-Squares Migration Method Based on Split-Step DSR[J]. Journal of Jilin University: Earth Science Edition, 2014,44(1): 369-374.

[14] 王新洲. 廣義平差的概括模型[J].武漢測繪科技大學學報, 2000, 25(3):257-260. Wang Xinzhou. The Comprehensive Model of Generalized Surveying Adjustment[J]. Journal of Wuhan Technical University of Surveying and Mapping, 2000, 25(3): 257-260.

[15] 崔希璋，於宗儔，陶本藻，等.廣義測量平差[M].武漢:武漢大學出版社,2009. Cui Xizhang, Yu Zongchou, Tao Benzao, et al. Geo-Spatial Information Science[M]. Wuhan: Wuhan University Press, 2009.

[16] 陶本藻. 測量數據處理的統(tǒng)計理論和方法[M].北京:測繪出版社,2007. Tao Benzao. Statistic Theory and Method of Surveying Data Processing[M]. Beijing: Surveying and Mapping Press, 2007.

[17] 王新洲，陶本藻，邱衛(wèi)寧，等.高等測量平差[M].北京:測繪出版社,2010. Wang Xinzhou, Tao Benzao, Qiu Weining, et al. Advanced Surveying Adjustment[M]. Beijing: Surveying and Mapping Press,2010.

[18] 劉國林. 近代測量平差理論與方法[M].徐州:中國礦業(yè)大學出版社,2012. Liu Guolin. The Principle and Methods of Modern Adjustment of Surveying[M]. Xuzhou: China University of Mining and Technology Press, 2012.

[19] 黃杰. 最小二乘濾波推估與配置的應用研究[J]. 桂林工學院學報, 1995, 15(1):97-103. Huang Jie. Study of Application of Least-Squares Filtering, Predication and Collocation[J]. Journal of Guilin Institute of Technology, 1995, 15(1):97-103.

[20] 趙龍，陳哲. 新型聯邦最小二乘濾波算法及應用[J].自動化學報, 2004, 30(6):897-904. Zhao Long, Chen Zhe. A New Type of Federated Least Square Filtering Algorithm and Its Application[J]. Acta Automatica Sinica, 2004, 30(6):897-904.

[21] 周一宇. 阻尼的非線性最小二乘濾波算法[J].國防科技大學學報, 1990, 12(4):103-107. Zhou Yiyu. Damped Nonlinear Squares Filtering Algorithm[J]. Journal of National University of Defense Technology, 1990, 12(4):103-107.

Data Processing of Deformation Monitoring Based on Least Square Filtering

Li Weidong1, Lin Nan1,2, Liu Deli1, Sun Xiaolei1

1.College of Surveying and Prospecting Engineering, Jilin Architecture University, Changchun 130118,China 2.College of GeoExploration Science and Technology, Jilin University, Changchun 130026,China

Total station is widely used in various measurements coordinates as the observation values play an important role in the data processiong. The authors adjusted the coordinate observation values combined with other conventional observations deformation data using the least square filter. The results indicated that the precision was obviously improved with the 1.35 mm decrease of maximum point error and 0.94 mm decrease of the weakest point error, and the constraints of different observation also increased the reliability of the least square filter adjustment.

least square; filtering; deformation monitoring; coordinate value

10.13278/j.cnki.jjuese.201406307.

2014-04-18

吉林省科技發(fā)展計劃項目(20120437)；國家自然科學基金項目(41072244)

李偉東(1967--)，男，副教授，主要從事測量誤差理論及變形監(jiān)測研究，E-mail:349127577@qq.com

林楠(1984--)，男，講師，主要從事工程變形監(jiān)測及地學信息工程研究，E-mail:linnanzc@126.com。

10.13278/j.cnki.jjuese.201406307

P642.3

A

李偉東，林楠，劉德利，等. 用于變形監(jiān)測的最小二乘濾波數據處理.吉林大學學報:地球科學版,2014,44(6):2068-2072.

Li Weidong, Lin Nan, Liu Deli, et al. Data Processing of Deformation Monitoring Based on Least Square Filtering.Journal of Jilin University:Earth Science Edition,2014,44(6):2068-2072.doi:10.13278/j.cnki.jjuese.201406307.