模糊語(yǔ)言多屬性群決策的客觀綜合賦權(quán)方法

龐繼芳，王寶麗

1.山西大學(xué)經(jīng)濟(jì)與管理學(xué)院，太原 030006

2.山西大學(xué)計(jì)算機(jī)與信息技術(shù)學(xué)院，太原 030006

模糊語(yǔ)言多屬性群決策的客觀綜合賦權(quán)方法

龐繼芳1，2，王寶麗2

1.山西大學(xué)經(jīng)濟(jì)與管理學(xué)院，太原 030006

2.山西大學(xué)計(jì)算機(jī)與信息技術(shù)學(xué)院，太原 030006

1 引言

為了保證決策的科學(xué)性和合理性，在社會(huì)、經(jīng)濟(jì)、工程、管理、軍事等領(lǐng)域常采用多屬性群決策的方法[1-3]。由于事務(wù)的復(fù)雜性、不確定性以及人類思維的模糊性，具有不確定性、不完全性的多屬性群決策問(wèn)題已成為當(dāng)前研究的一個(gè)重要熱點(diǎn)。文獻(xiàn)[4]針對(duì)基于三角模糊數(shù)的多屬性群決策問(wèn)題，給出一個(gè)確定屬性值權(quán)重的方法，并通過(guò)求解線性規(guī)劃模型來(lái)確定屬性權(quán)重。文獻(xiàn)[5-6]通過(guò)將不確定語(yǔ)言變量轉(zhuǎn)換為梯形模糊數(shù)，分別利用理想點(diǎn)法（TOPSIS）和優(yōu)化模型研究了多粒度不確定語(yǔ)言的群決策方法。文獻(xiàn)[7]利用動(dòng)態(tài)直覺(jué)模糊加權(quán)平均（DIFWA）算子和混合加權(quán)平均（HWA）算子，提出一種基于直覺(jué)模糊TOPSIS的動(dòng)態(tài)多屬性群決策交互方法。文獻(xiàn)[8]定義了直覺(jué)梯形模糊數(shù)的幾種集結(jié)算子，并提出了相應(yīng)的多準(zhǔn)則群決策方法。文獻(xiàn)[9]提出了誘導(dǎo)型區(qū)間直覺(jué)模糊混合平均（I-IIFHA）算子和誘導(dǎo)型區(qū)間直覺(jué)模糊混合幾何（I-IIFHG）算子，并給出一種區(qū)間直覺(jué)模糊多屬性群決策方法。文獻(xiàn)[10]針對(duì)具有語(yǔ)言型、直覺(jué)模糊數(shù)和區(qū)間直覺(jué)模糊數(shù)三種評(píng)價(jià)信息的混合型多屬性群決策問(wèn)題，在統(tǒng)一化后，定義了基于支持度的屬性權(quán)重確定方法和基于熵值的專家權(quán)重確定方法，給出了相應(yīng)的多屬性群決策方法。文獻(xiàn)[11]提出了基于直覺(jué)語(yǔ)言信息的多屬性群決策方法。文獻(xiàn)[12-13]對(duì)直覺(jué)不確定語(yǔ)言信息的集成問(wèn)題進(jìn)行了研究，定義了直覺(jué)不確定語(yǔ)言數(shù)的運(yùn)算法則、期望值、得分函數(shù)和精確函數(shù)，提出了一系列集結(jié)算子，并在此基礎(chǔ)上，給出了幾種屬性權(quán)重確知的直覺(jué)不確定語(yǔ)言多屬性群決策方法。

直覺(jué)不確定語(yǔ)言數(shù)集合了直覺(jué)模糊數(shù)和不確定語(yǔ)言變量的特點(diǎn)，在現(xiàn)實(shí)的決策過(guò)程中具有較強(qiáng)的實(shí)用價(jià)值，更適于表示定性的語(yǔ)言型信息，滿足評(píng)價(jià)需要。目前，關(guān)于屬性權(quán)重和專家權(quán)重完全未知的直覺(jué)不確定語(yǔ)言多屬性群決策方法的研究尚不多見(jiàn)。且現(xiàn)有的權(quán)重確定方法大都只從某一側(cè)面對(duì)權(quán)重進(jìn)行度量和刻畫(huà)，得到的權(quán)重信息比較片面，無(wú)法全面綜合地反映專家評(píng)價(jià)信息之間的關(guān)系。

本文在借鑒已有研究成果的基礎(chǔ)上，深入研究直覺(jué)不確定語(yǔ)言多屬性群決策中權(quán)重的客觀確定方法。首先，定義了直覺(jué)不確定語(yǔ)言數(shù)的不確定度以及距離測(cè)度。進(jìn)而，通過(guò)比較和分析單個(gè)專家內(nèi)部以及專家群體之間評(píng)價(jià)值的具體情況，提出了基于離差最大化和熵值的屬性綜合賦權(quán)模型以及基于不確定度和偏離度的專家綜合賦權(quán)模型，并給出了基于客觀綜合賦權(quán)模型的直覺(jué)不確定語(yǔ)言多屬性群決策方法。本文所提出的方法有效地解決了直覺(jué)不確定語(yǔ)言多屬性群決策中屬性及專家的客觀賦權(quán)問(wèn)題，得到的綜合權(quán)重能夠較為全面、客觀的反映屬性及專家的重要性。

2 直覺(jué)不確定語(yǔ)言數(shù)的相關(guān)概念

設(shè)S={sα|α=0,1,…,l}表示語(yǔ)言術(shù)語(yǔ)集[14-15]，其中sα表示語(yǔ)言術(shù)語(yǔ)，特別地，s0和sl分別表示語(yǔ)言術(shù)語(yǔ)的下限和上限，l為偶數(shù)。例如，S可取S={s0=極差,s1=很差,s2=差,s3=一般,s4=好,s5=很好,s6=極好}。

設(shè)s～=[sa,sb]，sa,sb∈S且a≤b，sa,sb分別是s～的下限和上限，則稱為不確定語(yǔ)言變量[16]。

定義1（直覺(jué)模糊集）設(shè)X為一非空集合，A={x,uA(x),vA(x)|x∈X}為直覺(jué)模糊集[17]，其中，uA(x)和vA(x)分別為X中元素x屬于X的隸屬度和非隸屬度，uA(x)、vA(x)∈[0,1]且滿足條件0≤uA(x)+vA(x)≤1。

W位置加權(quán)向量可以根據(jù)實(shí)際需要確定，也可以由組合數(shù)確定，計(jì)算公式如下[18]：

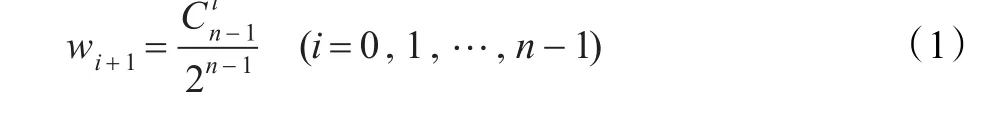
3 直覺(jué)不確定語(yǔ)言多屬性群決策的客觀綜合賦權(quán)方法

為了便于對(duì)直覺(jué)不確定語(yǔ)言數(shù)進(jìn)行比較和分析，下面首先給出不確定度和距離測(cè)度的定義。

3.1 屬性權(quán)重的確定

（1）基于離差最大化的屬性客觀權(quán)重

離差最大化賦權(quán)公式可用來(lái)確定單個(gè)專家內(nèi)部各屬性的客觀權(quán)重[19]。對(duì)于單個(gè)專家而言，若其在某一屬性下關(guān)于所有方案的評(píng)價(jià)值具有較小的差異，則說(shuō)明該屬性對(duì)方案決策與排序所起的作用較小，應(yīng)賦予其較小的權(quán)重；反之，應(yīng)賦予其較大的權(quán)重。

屬性Cj在專家ek下基于離差最大化的客觀權(quán)重的計(jì)算公式如下：

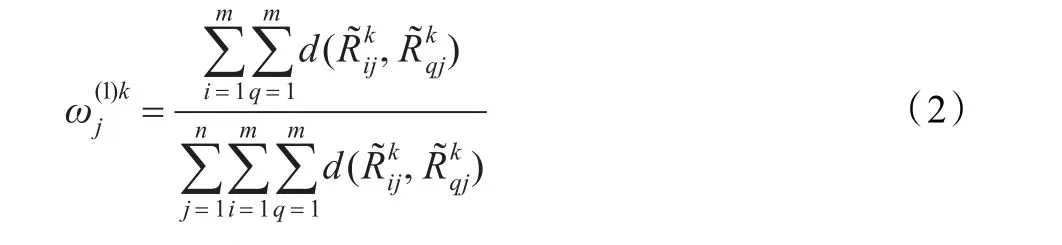
（2）基于熵值的屬性客觀權(quán)重

專家群體對(duì)同一方案在同一屬性下的評(píng)價(jià)越一致，則關(guān)于該方案在該屬性下的群決策結(jié)果越有效，應(yīng)賦給該屬性較大的權(quán)重；反之，則越無(wú)效，應(yīng)賦給該屬性較小的權(quán)重[20]。下面利用信息熵來(lái)衡量專家群體在某個(gè)屬性下評(píng)價(jià)結(jié)果的一致性，熵值越大，屬性權(quán)重就越大。將熵值歸一化后即得到屬性的客觀權(quán)重。具體計(jì)算方法如下：

首先通過(guò)計(jì)算期望值對(duì)直覺(jué)不確定語(yǔ)言數(shù)進(jìn)行去模糊化處理，接著計(jì)算專家群體關(guān)于方案Ai在屬性Cj下的期望值的信息熵Iij：

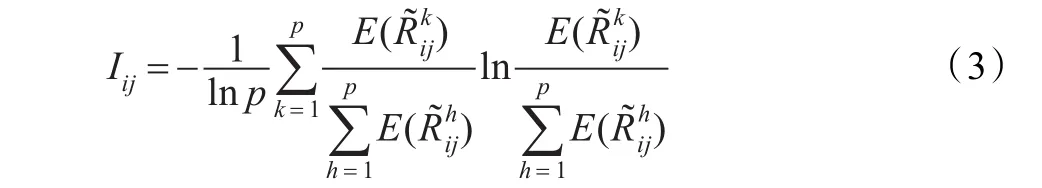
進(jìn)而可得專家群體關(guān)于方案集在屬性Cj下的平均信息熵Ij：

（3）屬性綜合客觀權(quán)重

基于離差最大化的屬性權(quán)重是通過(guò)計(jì)算各專家內(nèi)部在各屬性下方案評(píng)價(jià)值的差異程度來(lái)刻畫(huà)屬性重要性，基于熵值的屬性權(quán)重則是通過(guò)計(jì)算專家群體在各屬性下方案評(píng)價(jià)值的一致程度來(lái)刻畫(huà)屬性重要性。為了得到更加全面的屬性權(quán)重信息，可由決策者根據(jù)具體決策問(wèn)題設(shè)定參數(shù)α(0≤α≤1)對(duì)兩類權(quán)重進(jìn)行集結(jié)，則可得專家ek下屬性Cj的綜合客觀權(quán)重為：

3.2 專家權(quán)重的確定

（1）基于不確定度的專家客觀權(quán)重

利用定義4及屬性綜合客觀權(quán)重，計(jì)算專家ek給出

的個(gè)體決策矩陣R～k=[R～kij]m×n的不確定度?(R～k)：

專家所給出的個(gè)體決策矩陣的不確定度越小，表明該專家的決策越精確，應(yīng)賦給其較大的權(quán)重；反之，應(yīng)賦給其較小的權(quán)重。由此，給出專家ek基于不確定度的權(quán)重計(jì)算公式如下：

（2）基于偏離度的專家客觀權(quán)重

由于群決策是多個(gè)專家共同協(xié)商的過(guò)程，最終的決策結(jié)果反映了專家意見(jiàn)的妥協(xié)，應(yīng)當(dāng)趨于一致。因此可以根據(jù)專家個(gè)體決策與群體決策之間的偏離度來(lái)確定專家權(quán)重。與群體決策差異越大的專家，其與群體的共同意愿偏離越遠(yuǎn)，應(yīng)賦給其較小的權(quán)重，減弱該專家對(duì)群體決策結(jié)果的影響；反之，偏離度越小，表明該專家的決策與群體決策越一致，應(yīng)賦給其較大的權(quán)重，以提高專家群體的共識(shí)度。具體計(jì)算方法如下：

利用距離公式及屬性綜合客觀權(quán)重，計(jì)算專家ek與群體之間的偏離度f(wàn)k：

（3）專家綜合客觀權(quán)重

基于不確定度的專家權(quán)重通過(guò)比較各專家決策信息的精確程度來(lái)反映專家的重要性，基于偏離度的專家權(quán)重則通過(guò)計(jì)算各專家決策信息與群體決策信息之間的吻合程度來(lái)反映專家的重要性。為了得到更加全面的專家權(quán)重信息，可由決策者根據(jù)具體決策問(wèn)題設(shè)定參數(shù)β(0≤β≤1)對(duì)兩類權(quán)重進(jìn)行集結(jié)，則可得專家ek的綜合客觀權(quán)重為：

4 基于客觀綜合賦權(quán)模型的直覺(jué)不確定語(yǔ)言多屬性群決策方法

基于上述綜合權(quán)重計(jì)算模型，給出如下直覺(jué)不確定語(yǔ)言多屬性群決策方法：

步驟1根據(jù)定義5計(jì)算各專家在各屬性下關(guān)于兩兩方案對(duì)之間的距離，進(jìn)而利用式（2）計(jì)算各專家下各屬性基于離差最大化的客觀權(quán)重(k=1,2,…,p;j=1,2,…,n)。

步驟2計(jì)算各專家下所有評(píng)價(jià)值的期望值，進(jìn)而利用式（3）、（4）、（5）計(jì)算各屬性基于熵值的客觀權(quán)重(j=1,2,…,n)。

步驟3由決策者設(shè)定參數(shù)α的值，利用式（6）得到各專家下各屬性的綜合客觀權(quán)重(k=1,2,…,p;j=1,2,…,n)。

步驟4根據(jù)定義4計(jì)算各專家下所有評(píng)價(jià)值的不確定度，進(jìn)而利用式（7）、（8）計(jì)算各專家基于不確定度的客觀權(quán)重(k=1,2,…,p)。

步驟5根據(jù)定義5計(jì)算兩兩專家在各屬性下關(guān)于各方案評(píng)價(jià)值之間的距離，進(jìn)而利用式（9）、（10）計(jì)算各專家基于偏離度的客觀權(quán)重(k=1,2,…,p)。

步驟6由決策者設(shè)定參數(shù)β的值，利用式（11）得到專家的綜合客觀權(quán)重λk(k=1,2,…,p)。

步驟7利用屬性綜合客觀權(quán)重(k=1,2,…,p;j=1,2,…,n)及IULWAA算子對(duì)方案進(jìn)行集結(jié)，得到各專家關(guān)于各方案的個(gè)體綜合評(píng)價(jià)值

步驟8利用專家綜合客觀權(quán)重λk(k=1,2,…,p)及IULHA算子對(duì)各專家關(guān)于方案的個(gè)體綜合評(píng)價(jià)值進(jìn)行集結(jié)，得到各方案的群體綜合評(píng)價(jià)值

步驟9利用直覺(jué)不確定語(yǔ)言數(shù)的排序方法對(duì)R～i(i=1,2,…,m)進(jìn)行比較和排序，從而得到方案的最終排序并選出最優(yōu)方案。

5 實(shí)例分析

現(xiàn)有4個(gè)備選企業(yè)（即方案）{A1,A2,A3,A4}，從企業(yè)技術(shù)創(chuàng)新能力角度對(duì)企業(yè)進(jìn)行評(píng)價(jià)，評(píng)價(jià)指標(biāo)（即屬性）包括：創(chuàng)新資源投入能力(C1)、創(chuàng)新管理能力(C2)、創(chuàng)新傾向(C3)和研究開(kāi)發(fā)能力(C4)。現(xiàn)由3位專家{e1,e2,e3}對(duì)各企業(yè)按上述4項(xiàng)指標(biāo)進(jìn)行評(píng)估，各專家采用直覺(jué)不確定語(yǔ)言數(shù)給出的各企業(yè)的評(píng)價(jià)值見(jiàn)表1所示。專家采用的不確定語(yǔ)言評(píng)價(jià)集為S={s0,s1,s2,s3,s4,s5,s6}。請(qǐng)給出4家企業(yè)的技術(shù)創(chuàng)新能力的排序[12]。

具體決策過(guò)程如下：

步驟1根據(jù)表1計(jì)算各專家在各屬性下關(guān)于兩兩方案對(duì)之間的距離，并由此得到各專家下各屬性的客觀權(quán)重，見(jiàn)表2所示。

步驟2計(jì)算各專家下所有評(píng)價(jià)值的期望值，見(jiàn)表3所示。

在表3的基礎(chǔ)上，利用式（3）計(jì)算專家群體關(guān)于各方案在各屬性下的信息熵，見(jiàn)表4所示。

利用式（4）計(jì)算專家群體關(guān)于方案集在各屬性下的平均信息熵：I1=0.953，I2=0.942，I3=0.898，I4=0.948。利用式（5）計(jì)算各屬性基于信息熵的權(quán)重得：=0.255，

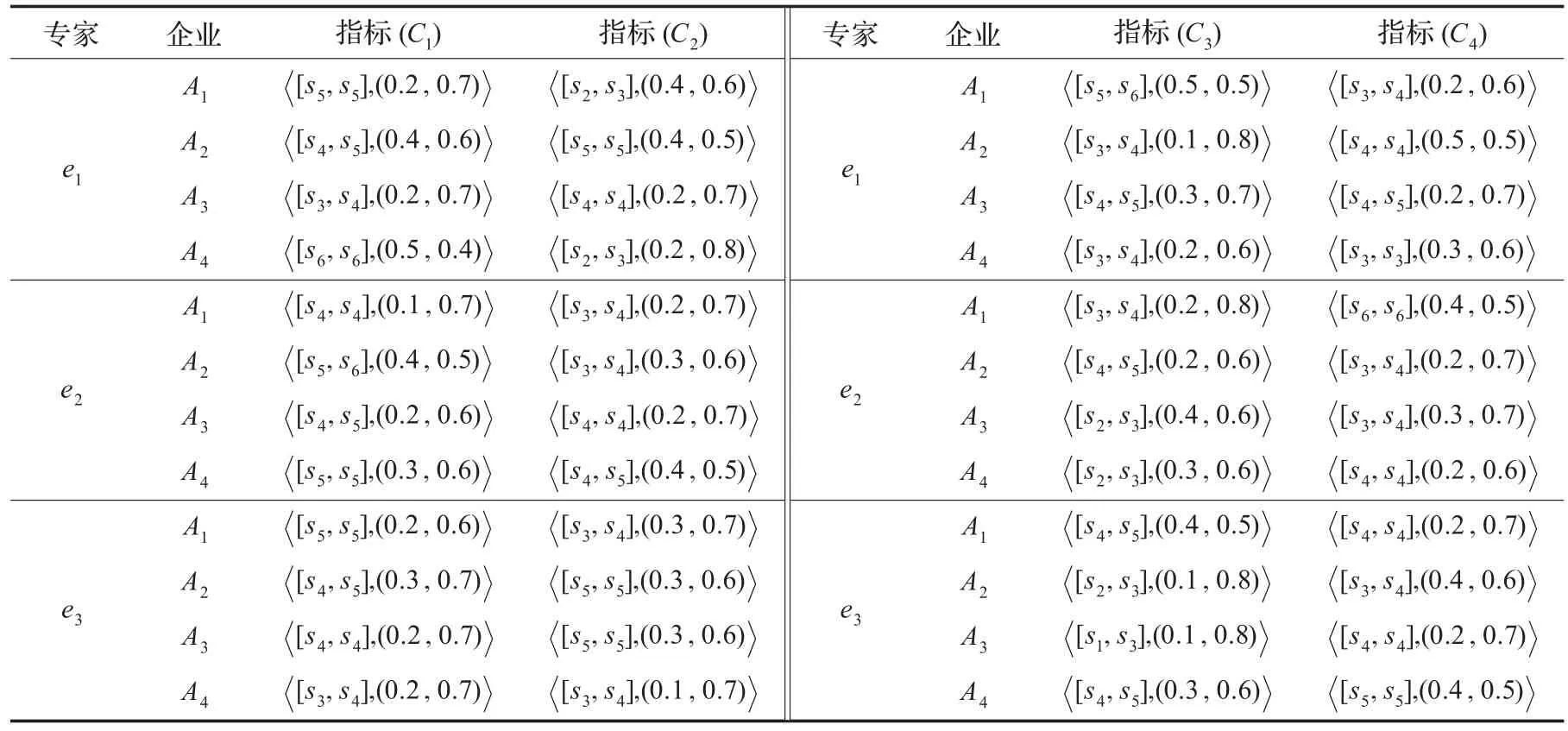
表13 位專家給出的4個(gè)企業(yè)不同指標(biāo)下的評(píng)價(jià)值

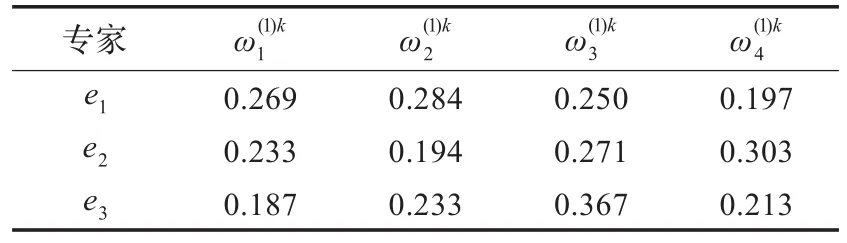
表2 各專家下各屬性基于離差最大化的客觀權(quán)重

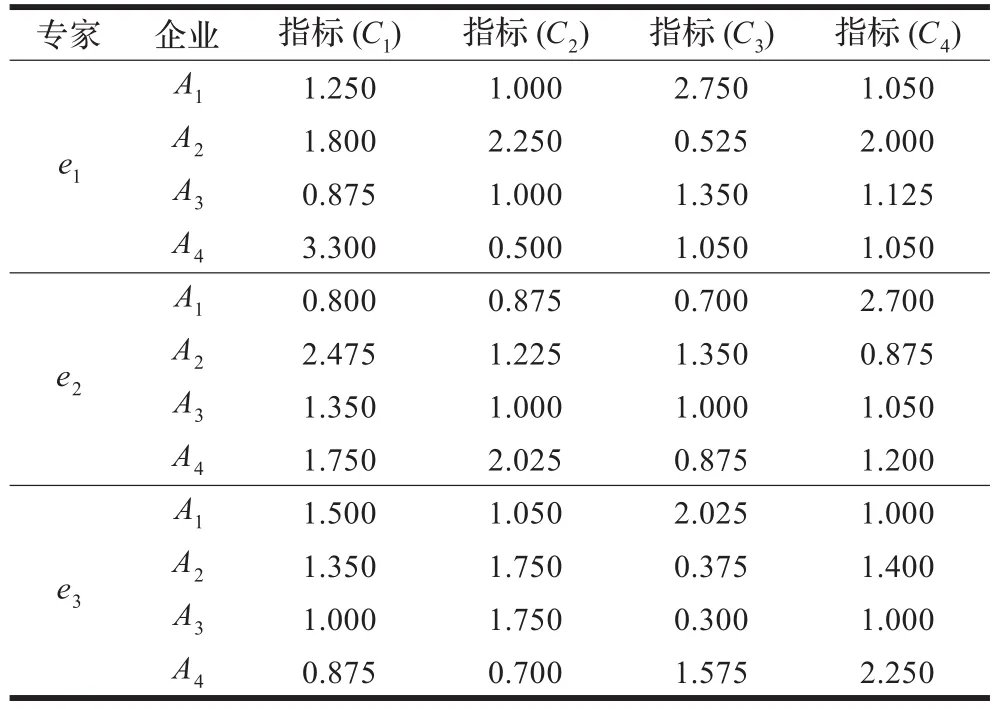
表3 各專家關(guān)于各方案在各屬性下評(píng)價(jià)值的期望值

表4 專家群體關(guān)于各方案在各屬性下的信息熵

步驟3設(shè)參數(shù)α=0.4，由式（6）可得各專家下屬性的綜合客觀權(quán)重，見(jiàn)表5所示。

步驟4根據(jù)定義4計(jì)算各專家下所有評(píng)價(jià)值的不確定度，見(jiàn)表6所示。

進(jìn)而利用式（7）計(jì)算各專家決策矩陣的不確定度：?(R～1)=0.360，?(R～2)=0.442，?(R～3)=0.399。由式（8）可得各專家的客觀權(quán)重為

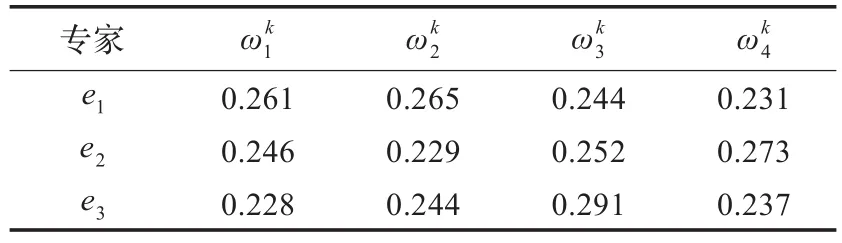
表5 各專家下各屬性基于離差最大化的客觀權(quán)重

表6 各專家下所有評(píng)價(jià)值的不確定度

步驟5根據(jù)定義5計(jì)算兩兩專家在各屬性下關(guān)于各方案評(píng)價(jià)值之間的距離，進(jìn)而利用式（9）計(jì)算各專家與群體之間的偏離度：f1=1.290，f2=1.406，f3=1.262。由式（10）可得各專家的權(quán)重為

步驟6設(shè)參數(shù)β=0.4，由式（11）可得專家的綜合客觀權(quán)重：λ1=0.351，λ2=0.307，λ3=0.341。

步驟7利用步驟3得到的屬性綜合客觀權(quán)重及IULWAA算子對(duì)方案進(jìn)行集結(jié)，得到各專家關(guān)于各方案的個(gè)體綜合評(píng)價(jià)值，見(jiàn)表7所示。

步驟8利用步驟6得到的專家綜合客觀權(quán)重及IULHA算子對(duì)各專家關(guān)于各方案的個(gè)體綜合評(píng)價(jià)值進(jìn)行集結(jié)，其中，位置向量W采用組合數(shù)公式產(chǎn)生，即W= (0.25,0.50,0.25)，則可得各方案的群體綜合評(píng)價(jià)值為：

表7 各專家關(guān)于各方案的個(gè)體綜合評(píng)價(jià)值

步驟9計(jì)算所有群體綜合評(píng)價(jià)值的期望值，得E(R～1)= 1.433，E(R～2)=1.368，E(R～3)=1.033，E(R～4)=1.387。按照期望值從大到小對(duì)所有方案進(jìn)行排序，可得方案的最終排序?yàn)锳1?A4?A2?A3，其中A1為最優(yōu)方案，即企業(yè)A1的技術(shù)創(chuàng)新能力最強(qiáng)。

6 結(jié)語(yǔ)

直覺(jué)不確定語(yǔ)言數(shù)是對(duì)直覺(jué)模糊數(shù)和不確定語(yǔ)言變量的擴(kuò)展，更適于表達(dá)模糊語(yǔ)言信息，具有較強(qiáng)的實(shí)用價(jià)值。本文在屬性及專家權(quán)重均未知的情況下，針對(duì)評(píng)價(jià)值為直覺(jué)不確定語(yǔ)言數(shù)的多屬性群決策問(wèn)題，提出了基于客觀綜合賦權(quán)模型的模糊群決策方法。該方法綜合考慮了評(píng)價(jià)值在單個(gè)專家內(nèi)部以及專家群體之間的取值和分布情況，得到的屬性權(quán)重及專家權(quán)重能較為全面、客觀地反映專家評(píng)價(jià)信息之間的關(guān)系，更好地刻畫(huà)屬性及專家的重要性。具體的應(yīng)用實(shí)例系統(tǒng)分析了該方法的全過(guò)程，說(shuō)明了該方法的有效性和可行性。本文提出的方法豐富和發(fā)展了模糊語(yǔ)言群決策的理論和方法。

[1]Rosello L，Sanchez M，Agell N，et al.Using consensus and distancesbetweengeneralizedmulti-attributelinguistic assessmentsforgroupdecision-making[J].Information Fusion，2014，17：83-92.

[2]Pang J F，Liang J Y.Evaluation of the results of multiattribute group decision-making with linguistic information[J].Omega，2012，40（3）：294-301.

[3]毛軍軍，王翠翠，姚登寶.基于多專家區(qū)間數(shù)的多屬性群決策方法[J].計(jì)算機(jī)應(yīng)用，2012，32（3）：649-653.

[4]楊威，史加榮，龐永鋒.模糊環(huán)境下部分權(quán)重信息的多屬性群決策方法[J].模糊系統(tǒng)與數(shù)學(xué)，2013，27（1）：118-123.

[5]Fan Z P，Liu Y.A method for group decision-making based on multi-granularity uncertain linguistic information[J].Expert Systems with Applications，2010，37（5）：4000-4008.

[6]Zhang Z，Guo C H.A method for multi-granularity uncertain linguistic group decision making with incomplete weightinformation[J].Knowledge-BasedSystems，2012，26：111-119.

[7]Su Z X，Chen M Y，Xia G P，et al.An interactive method fordynamicintuitionisticfuzzymulti-attributegroup decision making[J].Expert Systems with Applications，2011，38（12）：15286-15295.

[8]王堅(jiān)強(qiáng)，聶榮榮.基于直覺(jué)梯形模糊信息的多準(zhǔn)則群決策方法[J].系統(tǒng)工程理論與實(shí)踐，2012，32（8）：1747-1753.

[9]梁昌勇，戚筱雯，張俊嶺，等.基于誘導(dǎo)型區(qū)間直覺(jué)模糊混合算子的群決策方法[J].系統(tǒng)工程學(xué)報(bào)，2012，27（6）：759-771.

[10]戚筱雯，梁昌勇，黃永青，等.基于混合型評(píng)價(jià)矩陣的多屬性群決策方法[J].系統(tǒng)工程理論與實(shí)踐，2013，33（2）：473-481.

[11]Liu P D.Some generalized dependent aggregation operators with intuitionistic linguistic numbers and their application to group decision making[J].Journal of Computer and System Sciences，2013，79（1）：131-143.

[12]劉培德，張新.直覺(jué)不確定語(yǔ)言集成算子及在群決策中的應(yīng)用[J].系統(tǒng)工程理論與實(shí)踐，2012，32（12）：2704-2711.

[13]Liu P D，Jin F.Methods for aggregating intuitionistic uncertain linguistic variables and their application to group decision making[J].Information Sciences，2012，205（1）：58-71.

[14]Bordogna G，F(xiàn)edrizzi M，Passi G.A linguistic modelling of consensus in group decision making based on OWA operators[J].IEEETransactionsonSystems，Manand Cybernetics，1997，27（1）：126-132.

[15]Herrera F，Martinez L.A model based on linguistic 2-tuples fordealingwithmulti-granularhierarchicallinguistic contexts in multi-expert decision-making[J].IEEE Transaction on Systems，Man and Cybernetics，2001，31（2）：227-233.

[16]Xu Z S.Induced uncertain linguistic OWA operators applied to group decision making[J].Information Fusion，2006，7（2）：231-238.

[17]Atanassov K T.Intuitionistic fuzzy sets[J].Fuzzy Sets and Systems，1986，20（1）：87-96.

[18]王煜，徐澤水.OWA算子賦權(quán)新方法[J].數(shù)學(xué)的實(shí)踐與認(rèn)識(shí)，2008，38（3）：51-61.

[19]徐澤水.不確定多屬性決策方法及應(yīng)用[M].北京：清華大學(xué)出版社，2004.

[20]周榮喜，范福云，何大義，等.多屬性群決策中基于數(shù)據(jù)穩(wěn)定性與主觀偏好的綜合熵權(quán)法[J].控制與決策，2012，27（8）：1169-1174.

PANG Jifang1，2,WANG Baoli2

1.School of Economic and Management,Shanxi University,Taiyuan 030006,China
2.School of Computer and Information Technology,Shanxi University,Taiyuan 030006,China

For the Multi-Attribute Group Decision Making（MAGDM）problems,in which the weights of both attributes and experts are unknown and the evaluation values are intuitionistic uncertain linguistic variables,a fuzzy group decision making method based on the objective comprehensive weighting model is proposed.By defining the concepts of uncertainty and distance measure,the evaluation values within single expert and between experts are analyzed.Then the objective comprehensive weighting model of attributes based on maximizing deviations and entropy and the objective comprehensive weighting model of experts based on uncertainty and deviation are established respectively.Furthermore,a method based on the objective comprehensive weights for MAGDM with intuitionistic uncertain linguistic information is proposed. A case study is presented to illustrate the feasibility and practicability of the proposed method.

intuitionistic uncertain linguistic variables;multi-attribute group decision making;uncertainty;distance;entropy; deviation;weight

針對(duì)一類屬性及專家權(quán)重完全未知且評(píng)價(jià)值為直覺(jué)不確定語(yǔ)言數(shù)的多屬性群決策問(wèn)題，提出一種基于客觀綜合賦權(quán)模型的模糊群決策方法。通過(guò)定義直覺(jué)不確定語(yǔ)言數(shù)的不確定度和距離測(cè)度，對(duì)單個(gè)專家內(nèi)部以及專家群體之間的評(píng)價(jià)值進(jìn)行分析，分別建立基于離差最大化和熵值的屬性綜合賦權(quán)模型以及基于不確定度和偏離度的專家綜合賦權(quán)模型，提出一種基于客觀綜合權(quán)重的直覺(jué)不確定語(yǔ)言多屬性群決策方法。通過(guò)實(shí)例分析表明了該方法的可行性和實(shí)用性。

直覺(jué)不確定語(yǔ)言數(shù)；多屬性群決策；不確定度；距離；熵；偏離度；權(quán)重

A

TP393

10.3778/j.issn.1002-8331.1402-0214

PANG Jifang,WANG Baoli.Objective comprehensive weighting method for multi-attribute group decision making with fuzzy linguistic information.Computer Engineering and Applications,2014,50（22）：1-6.

國(guó)家自然科學(xué)基金重點(diǎn)項(xiàng)目（No.71031006）；國(guó)家青年科學(xué)基金（No.71301090）；山西省回國(guó)留學(xué)基金（No.2013-101）。

龐繼芳（1980—），女，博士研究生，講師，研究領(lǐng)域?yàn)閿?shù)據(jù)挖掘與決策分析。王寶麗（1982—），女，博士研究生，講師，研究領(lǐng)域?yàn)榱Ｓ?jì)算與智能決策。E-mail：purplepjf@sxu.edu.cn

2014-02-20

2014-05-23

1002-8331（2014）22-0001-06

CNKI網(wǎng)絡(luò)優(yōu)先出版：2014-06-26,http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1402-0214.html