DSm組合規則的改進及其在直覺模糊集上的拓展

唐長春，敖志剛，宮云祥，張康益，王有成

解放軍理工大學 野戰工程學院，南京 210007

DSm組合規則的改進及其在直覺模糊集上的拓展

唐長春，敖志剛，宮云祥，張康益，王有成

解放軍理工大學 野戰工程學院，南京 210007

隨著傳感器、網絡等微電子和通信技術的深入發展，人們能夠獲取到的信息呈現爆炸式增長，這對人們處理信息的能力提出了更高要求。多源信息融合技術應運而生，其給人們提供了一條高效、精確應用信息的途徑[1]。信息的多源性是信息融合的基礎，而信息的不確定性、不完善是信息融合最本質的動因。對于多源不確定信息的融合問題，目前已有很多方法，包括概率論、模糊集、貝葉斯理論、神經網絡、DS證據理論（Dempster-Shafer Theory，DST）等，其中DST是一種具有處理不確定信息能力的不精確推理理論[2-4]，在不確定性信息的表示、推理、融合等方面的優勢已得到了廣泛認同。但DST處理沖突信息的能力不強，對于高度沖突的證據合成結果較差。針對DST的不足，許多學者提出了改進方法。DSmT（Dezert-Smarandache Theory）是由法國的Jean Dezert博士和美國的Florentin Smarandache教授提出和發展的一種將似事而非和自相矛盾推理方法用于信息融合的新理論[5]。DSmT可看作是DST的拓展，其在處理沖突信息和不完善信息等方面的能力得到了明顯的加強，因此受到了普遍關注。在實踐中，發現DSmT也存在著非常致命的問題，即DSmT的信度組合結果往往很難給決策提供有效的依據，甚至會增加證據源信息原有的不確定性。

表1 m個傳感器識別信息的DSmT組合結果

本文對DSmT及其存在的問題進行了較深入的分析，并在其基礎上提出了一種新的基于沖突再分配的證據組合規則（K-DSm規則）。為進一步提高DSmT處理沖突、模糊和不精確信息的能力，研究了DSmT在直覺模糊集上的拓展，將傳統的信度賦值函數替換為直覺模糊信度賦值映射，并討論了直覺模糊拓展后的信度組合規則。最后，通過數值實例對提出的方法進行了驗證。

1 DSmT及其存在的問題分析

DSmT對證據理論中的Shafer模型作了修改，提出了DSm模型，該模型定義了一個廣義的鑒別框Θ，減少了對鑒別框中焦元的約束限制，允許Θ中的元素存在交集，從而極大提高了DSmT組合沖突信息的能力，并且使其能夠有效處理具有模糊邊界、不可細分的信息融合問題，如高/矮、胖/廋等。跟DST一樣，DSmT也是采用正交和的方式對焦元進行組合，所不同的是，DSm組合規則不需要歸一，其中的緣故本質上即是DSm模型保留了所有沖突焦元的信度賦值。DSm組合規則的具體形式如下：

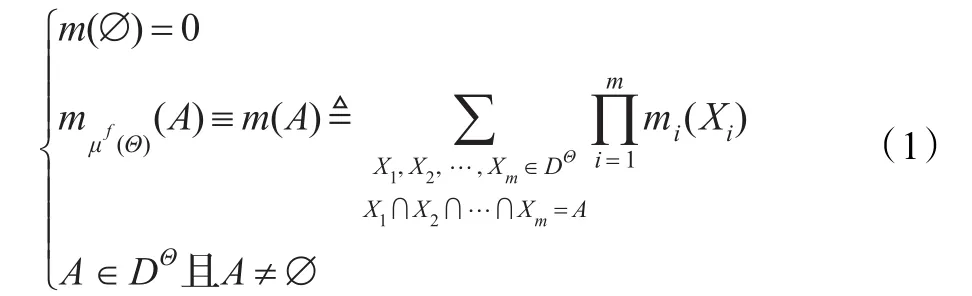
其中，DΘ是由Θ中的命題，以及通過∪和∩運算組成的所有復合命題的集合，稱為超冪集。DSm組合規則具有良好的交換性和結合性，符合證據源的合取一致原理；由于這種組合規則不需要歸一化過程，從而能夠避免出現類似于DST在高沖突情況下產生的問題；相比DST，DSm組合規則的組合結果更符合人類的直覺。在實際應用中，DSmT表現出的優勢是明顯的，但同時也存在諸多缺陷和不足，先看一個簡單的例子：

假設在某次聯合訓練中，基地上有m個傳感器同時監測到某空域出現的目標，各傳感器在本地對監測到的數據進行處理后將識別結果發送到聯合訓練導控中心，以得到一致和準確的預測。假定這m個傳感器得到了如下完全一致的結果：

mi(J)=0.8，mi(H)=0.15 ，mi(Θ)=0.05，（i=1，2，…，m，J代表殲擊機，H代表轟炸機）

mi(Θ)表示傳感器i對未知信息(It=J∪H)的信度賦值。假如聯合訓練導控中心采用DSmT對這些傳感器的識別信息進行組合，m取不同值時得到的結果如表1所示。

本例類似于文獻[6]給出的例子。在這個例子中，m個傳感器相當于m個證據源。由于這m個證據源完全一致，并且分配給命題J的信度較大，按照正常的邏輯，它們的組合結果應該能夠減小信息的不確定性，同時進一步增大命題J的信度。但是，從表1中發現隨著證據源數目的增多，組合結果中分配給主焦元的信度不斷減小，大量信度賦給了主焦元的交集，這種現象是異常的，特別是命題J的信度逐漸減小趨近于0，違背了人類直覺。顯然，根據表1所示的組合結果，難以對目標進行識別。

從上述例子中，可以發現DSmT的一個重要缺陷，即在某些情況下，DSm組合規則的組合結果不但不能減小信息的不確定性，反而會增加信息的不確定性。究其原因，可以從兩方面考慮，即模型和組合規則。DSmT建立在DSm模型上，允許鑒別框中的焦元存在交集既是DSm模型的優勢，同時又給DSm組合規則帶來了隱患。上文提到，DSmT采用正交和規則對焦元的信度進行組合，在這種組合規則下，如果允許保留沖突焦元，那么沖突焦元一經產生，便不會消逝，賦予它的信度也不會被再次分配，只能進行重組、傳遞和累積[6]，這即是出現上例所示問題的原因。

應用DSmT的另一個困難是其計算復雜度有可能出現組合爆炸現象[7-8]。DSmT對問題的分析和處理建立在DSm模型和超冪集上 DΘ，而 DΘ的勢|DΘ|按22|Θ|數量級遞增，同時由于組合過程中沖突焦元的累積，會引發焦元呈爆炸式增長，造成計算量和存儲量的“爆炸”，當|Θ|＞6時，DΘ的計算和存儲將面臨極大的困難，并且隨著證據源的不斷補充，計算的復雜度會進一步提高。

針對DSmT存在的不足，文獻[6]提出了一種基于沖突再分配的CR-DSmT組合公式，使組合結果中分配給主焦元的信度得到了合理的增加；文獻[9]則提出了一種快速分層遞階DSmT近似推理融合方法，有效提高了算法的計算效率；文獻[8]亦研究了優化DSmT計算復雜度的方法；此外，還有許多文獻從不同的角度對DSmT進行了改進[10-11]。盡管上述文獻都在一定程度上改善了DSmT的相關性能，但它們大多只從單一角度去尋求局部性能上的提高，而忽視了算法整體上的優化，因此，在應用上仍有一定的局限。受經典DST組合規則的歸一化過程和文獻[6]的啟發，本文提出了一種新的基于沖突再分配的信度組合規則，稱之為K-DSm組合規則。

2 K-DSm證據組合規則

如何處理沖突是證據理論體系中的一個關鍵問題。由于大部分組合規則都是采用正交和（析取）的方式來組合證據，而這種方式必定會引起多個相異主焦元的相交（∩）運算，由此便會產生沖突焦元。所謂沖突焦元即是在證據組合過程中，產生的含有交集的焦元，如(θ1∪θ2)∩θ3。由于Shafer模型規定命題之間完全互斥，因此，在DST的組合結果中，沖突焦元的信度賦值始終為0，這是DST處理沖突能力低的本質原因；DSm模型中雖保留了沖突焦元的信度賦值，但卻造成了沖突的累積，增加了組合證據的不確定性；Yager將沖突焦元視為不可靠的信息，而將其信度分配給了完全未知集[12]；Dubois和Prade反駁Yager的觀點，認為焦元之間的沖突表征的是一種競爭關系，沖突焦元的信度應在主焦元之間進行再分配[13]。實質上，沖突焦元既描述了主焦元之間的異性，同時也蘊含了主焦元之間的共性。如果采用DSm模型，那么兩個主焦元之間的交集必然屬于兩主焦元，即θ1∩θ2?θ1且θ1∩θ2?θ2，同時，從主觀上看交集部分包含的信息是不確定的，邏輯上亦有θ1∩θ2?It(It=θ1∪θ2∪…∪θn)。從而，綜合Yager和Dubois的觀點，本文認為沖突焦元的信度既應屬于未知的部分，同時應在主焦元之間進行再分配。并且既然沖突焦元不能提供有用的信息，那么完全可以在組合結果中將其去除，基于此，提出如下所示的K-DSm組合規則。

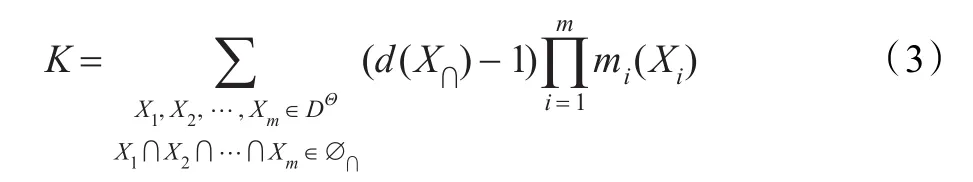
其中，X∩=X1∩X2∩…∩Xm即表示組合過程產生的沖突焦元，d(X∩)表示沖突焦元 X∩的信度被重復分配的次數，假設在 X∩中，直接與“∪”算子相連的主焦元個數為d∪(X∩)，則：

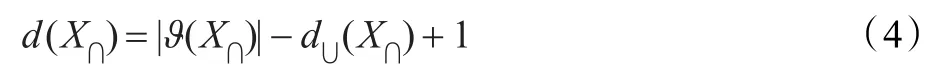
與經典DSm組合規則相比，K-DSm組合規則在組合結果中去除了沖突焦元，這不僅使得計算量和存儲量大為減少，同時也使得信度分配更為集中，從而促使主焦元能夠獲得更多的信度并且更容易收斂。K-DSm組合規則中含有歸一化系數K，K有別于DST中的沖突因子，它能夠消除由于沖突焦元信度被重復分配而造成的信度溢出，起到弱化沖突的作用。

應用K-DSm組合規則去解決上文中提到的例子時，得到如表2所示的結果。

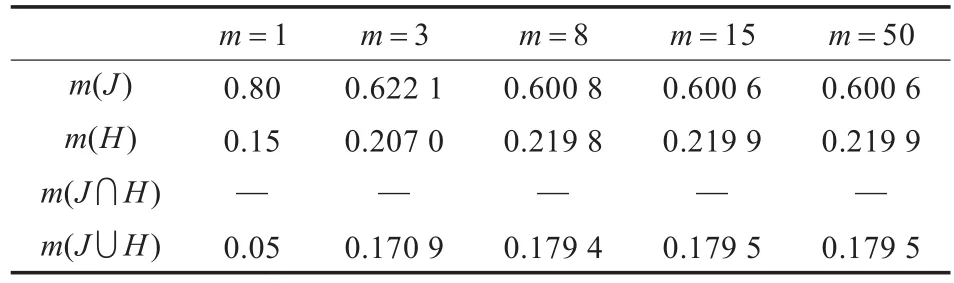
表2 m個傳感器識別信息的K-DSm組合結果

從表2中可以看出，隨著證據源的增多，各焦元的信度賦值逐漸收斂。在組合結果中，命題J的信度賦值稍微有所減少，而其他焦元的信度賦值卻有所增加，這是因為，在K-DSm組合規則中，各主焦元的地位被視為等同，在組合過程中同等地獲得了沖突焦元的信度，在某些情況下，這是不合理的，比如說本例。命題J對沖突焦元的影響顯然較大，其在信度分配中理應要占優勢，由于這考慮起來比較復雜，將在以后的工作中做進一步研究。盡管K-DSm組合規則也存在著不足，但它的組合結果仍然要優于DSm組合規則，根據表2所示的結果，可以很明確地判定目標為J。應用K-DSm組合規則去解決證據理論中常用的一個例子，即Zadeh問題時，同樣得到相比DSm組合規則更符合直覺的結果，進一步說明了K-DSm組合規則的優越性。

3 DSmT在直覺模糊集上的拓展

DST以及DSmT中的基本信度賦值都是一個單一的值，在概念上對應于模糊集理論中的隸屬函數，表征證據源對命題的支持程度。多數情況下，證據源不僅能提供支持命題為真的度量，同時也能提供反對命題為真的度量，這就意味著DST或DSmT的信度賦值方式不能完全描述證據源提供的信息，從而造成信息的流失，直接的后果是導致組合結果的精度下降，并且會增加證據源信息之間的沖突。直覺模糊集（Intuitionistic Fuzzy Sets，IFS）[14]同時引入了隸屬度、非隸屬度和猶豫度三個度量，相比模糊集，其能夠更加靈活和完整地描述模糊信息。因此，本文考慮將DSmT中的基本信度賦值擴展為一個直覺模糊數，以此來進一步增加DSmT處理模糊和沖突信度的能力。

定義1設Θ是DSm模型下的廣義鑒別框，DΘ是Θ的超冪集，則映射：

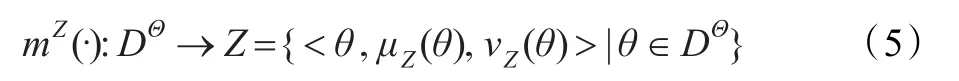
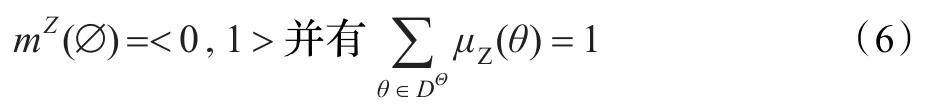
根據直覺模糊數的定義，有0≤μΖ(θ)+νΖ(θ)≤1，其中 μΖ(θ)與DSmT中的廣義基本信度賦值意義相同，表征證據源對命題θ的支持程度；νΖ(θ)則表示對命題θ的不信任度。同樣可以引入猶豫度πΖ(θ)的概念來描述對命題的不確定性度量，并且πΖ(θ)=1-μΖ(θ)-νΖ(θ)。

在DSmT的理論框架下，Bel(θ)是命題θ(θ∈DΘ)的廣義信度函數值，表示證據對命題θ完全支持的程度，若θ的余集為θˉ，則Bel(θˉ)表示證據對命題θ完全反對的程度。可以看出，Bel(θˉ)的特征意義與νΖ(θ)是一致的。因此，對于一個由經典DSm模型描述的信息融合問題，可以采用一種簡單且有效的方法來對廣義基本信度賦值進行擴展，得到直覺模糊信度賦值IFS_bba。方法即是：將μΖ(θ)取值為DSm模型中的廣義基本信度賦值m(θ)，νΖ(θ)取值為與之對應的Bel(θˉ)，則mZ(θ)=＜m(θ)，Bel(θˉ)＞，可以證明其是一個合適的IFS_bba。

在給出直覺模糊拓展后的證據組合規則前，先對一些符號進行說明。根據文獻[14]可以推出“⊕”和“?”算子具有以下的運算關系：

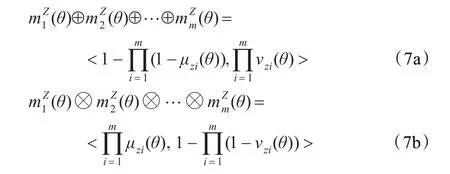
利用上述運算規則和定義的符號，可以方便地給出直覺模糊拓展后的證據組合規則，如下：

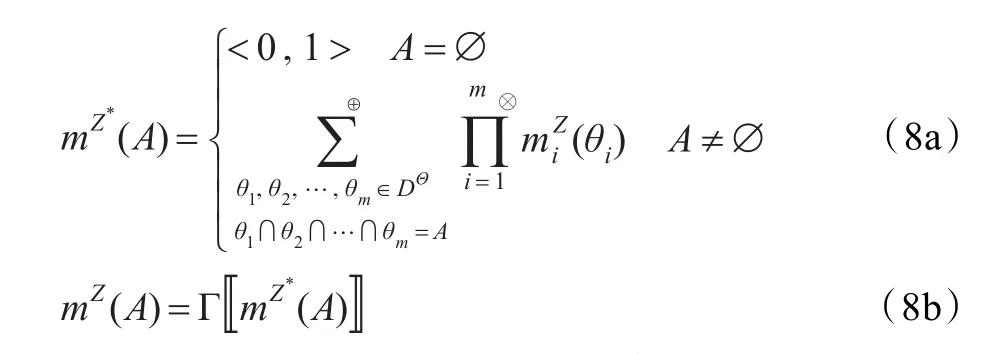
這里給出Γ?·?的一種簡單形式：?i=1，2，…，n

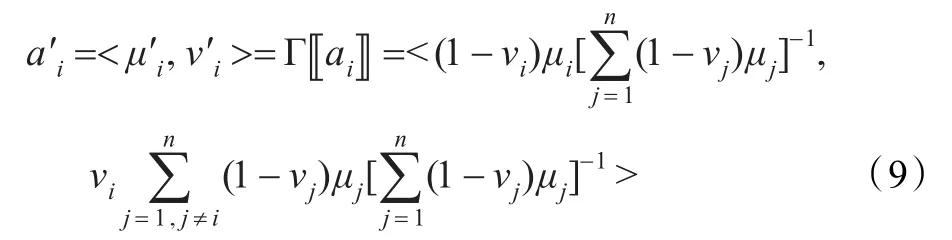
將DSmT在直覺模糊集上拓展之后，所有運算都變成了直覺模糊數之間的運算。根據直覺模糊DSm組合規則得到的焦元組合直覺模糊信度賦值仍是一個直覺模糊數。在得到所有焦元經證據組合后的直覺模糊信度賦值之后，就可以對它們根據相應直覺模糊信度賦值的大小進行排序，并做出最優決策。為比較直覺模糊信度賦值的大小，在此給出如下定義：

定義2設θ1，θ2∈DΘ，相應的直覺模糊信度賦值為：mZ(θ1)=＜μz(θ1)，νz(θ1)＞，mZ(θ2)=＜μz(θ2)，νz(θ2)＞，若滿足下列條件之一，則有mZ(θ1)＜mZ(θ2)：

（1）μz(θ1)-νz(θ1)＜μz(θ2)-νz(θ2)

（2）μz(θ1)-νz(θ1)=μz(θ2)-νz(θ2)且 μz(θ1)+νz(θ1)＜μz(θ2)+νz(θ2)

4 數值仿真及分析

雷達和紅外是兩種常用的探測設備。在實驗系統中分別采用這兩種設備對仿真目標進行識別。設定的仿真目標包括戰區戰略導彈TBM（T），殲擊機（J）以及誘餌（B），因此鑒別框為Θ={T，J，B}，采用自由DSm模型，即允許鑒別框Θ中的元素存在交集。關于探測設備對仿真目標的探測識別機理以及內部數據的處理過程，本文暫不討論，直接給出各傳感器對目標的識別報告，具體數據如表3所示。

表3 目標識別的廣義基本信度賦值分配

表4 目標識別的直覺模糊信度賦值分配

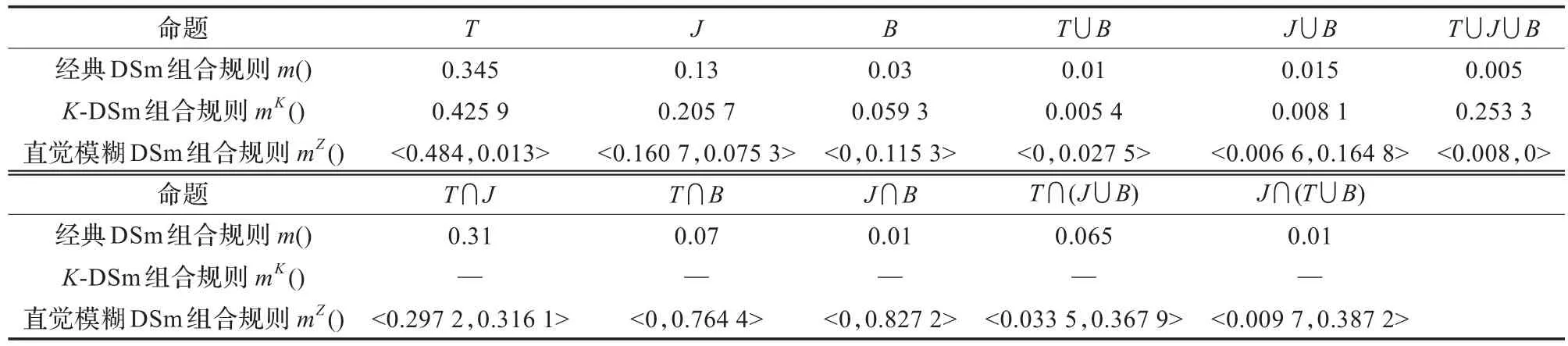
表5 目標識別的證據組合結果對比

步驟1構造初始的各焦元的直覺模糊信度賦值分配（IFS_bba）

構造方法如下：

（1）分別計算每個傳感器證據對各命題余集的廣義信度函數值；

（2）構造對應于各命題θi的直覺模糊信度賦值＜mj(θi)，＞。

步驟1的執行結果如表4所示。

步驟2對各傳感器的證據數進行組合

為方便進行比較分析，本例同時還運用了經典的DSm組合規則和K-DSm組合規則來對證據進行組合。采用各種組合規則得到的結果如表5所示。

步驟3決策分析

決策的方法是選取直覺模糊信度賦值最大的焦元作為最終的目標識別結果。

根據定義2，對表5中的直覺模糊信度賦值進行大小排序，很容易得到mZ(T)=＜0.484 4，0.013＞是其中最大的直覺模糊數，即焦元T的直覺模糊信度賦值最大，從而判定目標最有可能為TBM，顯然，這與基于DSm組合規則和K-DSm組合規則的識別結果是一致的。

在定義直覺模糊信度賦值時，將其中的肯定信任度等價于DSm模型下的廣義基本信度賦值。由于直覺模糊信度賦值更全面地描述了證據源提供的信息，在直覺模糊拓展DSm組合規則的證據組合過程中，有效發揮了直覺模糊信度賦值的優勢，焦元的肯定信任度和否定信任度的合成值能夠相互修正，使得組合結構更為準確和合理。從表5中可以發現，雖然根據三種組合規則，得出的結論一致，都是判定目標為TBM的可能性最大，但是它們包含的不確定性程度是存在差別的。在決策過程中，信度賦值分配越集中，則越有利于最優決策，即信息包含的不確定性越少。從組合結果來看，焦元T的直覺模糊信度賦值中的肯定信任度為0.484 4，大于經典DSm組合規則和K-DSm組合規則組合結果中焦元T的基本信度賦值，同時，焦元T的否定信任度很小，因此，相比其他兩種合成結果，基于直覺模糊拓展DSm組合規則的組合結果的決策具有最小的決策風險，從而為決策過程提供更可靠的支持。

需要指出，由于直覺模糊信度賦值包含了更多的信息，其所需要的存儲空間是基本信度賦值的兩倍；直覺模糊拓展DSm組合規則相比經典DSm和K-DSm組合規則的計算復雜度也更高，因此采用該規則需要付出的代價更高。但是從證據合成結果的合理性和準確性的角度來考慮，直覺模糊拓展DSm組合規則仍不失為一種有效的選擇。進一步研究和完善DSmT在直覺模糊集上的拓展方法和過程具有較高的理論和應用價值。

5 結語

本文的內容主要分為兩部分。第一部分從一個簡單的例子出發，指出DSmT的組合結果通常不能有效地減少信息的不確定性，并且存在計算復雜度高的問題，針對DSmT存在的缺陷，提出了一種新的基于沖突再分配的證據組合規則，即K-DSm組合規則，該規則在組合結果中清除了沖突焦元，并將沖突焦元的信度同時分配給了引起沖突的主焦元和完全的未知集，使得信度的分配更為合理；第二部分研究了DSmT在直覺模糊集上的拓展，將直覺模糊集在描述和處理模糊信息等方面的優勢引入到DSmT中，進一步增強了DSmT組合沖突、模糊和不精確證據信息的能力。本文為DSmT理論的完善和改進提供了兩種新的思路，但還不夠成熟，仿真結果初步驗證了這兩種思路的價值。

[1]潘泉.信息融合理論的基本方法與進展（II）[J].控制理論與應用，2012，29（10）：1233-1244.

[2]段新生.證據理論與決策、人工智能[M].北京：中國人民大學出版社，1993.

[3]韓德強.基于證據距離與不確定度的證據組合方法[J].紅外與毫米波學報，2011，30（5）：396-400.

[4]Yamada K.A new combination of evidence based on compromise[J].Fuzzy Sets and System，2008，159（13）：1689-1708.

[5]Smarandache F，Dezert J.Advances and applications of DSmT for information fusion，vol.1[M].Rehoboth，USA：American Research Press，2004.

[6]曲圣杰.沖突再分配DSmT及解決證據間矛盾的新方法[J].控制與決策，2009，24（12）：1856-1860.

[7]Li X，Dezert J，Smarandache F，et al.Evidence supporting measure of similarity for reducing the complexity in information fusion[J].Information Sciences，2011，181（10）：1818-1835.

[8]陳凱，楊俊安，陳昊.DSmT混合規則高復雜度優化[J].計算機工程，2010，36（7）：76-79.

[9]李新德.一種快速分層遞階DSmT近似推理融合方法（B）[J].電子學報，2011，39（3A）：31-36.

[10]胡麗芳，關欣，何友.一種新的基于DSmT的合成公式[J].火力與指揮控制，2009，34（7）：9-11.

[11]李鵬，黃心漢，王敏.DSmT框架下的自適應通用分配法則[J].計算機工程與應用，2010，46（6）：16-19.

[12]Yager R.On the Dempster-Shafer framework and new combination rules[J].Information Sciences，1987，41（2）：93-138.

[13]Dubois D，Prade H.Representation and combination of uncertainty with belief functions and possibility measures[J].Computational Intelligence，1998，4（3）：244-264.

[14]徐澤水.直覺模糊信息集成理論與應用[M].北京：科學出版社，2008.

TANG Changchun,AO Zhigang,GONG Yunxiang,ZHANG Kangyi,WANG Youcheng

College of Field Engineering,PLA University of Science and Technology,Nanjing 210007,China

Dezert-Smaradache Theory retains conflicting focal element in the combined result,which benefits the combination ability for conflict evidence,meanwhile,it results in the accumulation of conflicting information,and makes the composite reliability of main focal element reduce illogically.A new combination rule based on conflict redistribution is proposed to resolve the problem of DSmT.In order to further improve the DSmT performance in dealing with uncertain, highly conflicting and imprecise information,this paper researches the method to develop DSmT on the intuitionistic fuzzy sets.An intuitionistic fuzzy belief assignment mapping is defined to replace traditional belief assignment function, and the combination rule based on the new mapping is discussed in this paper.Numerical examples demonstrate the effectiveness of the proposed method.

information fusion;DSmT;conflict redistribution;intuitionistic fuzzy sets

DSmT在組合結果中保留了沖突焦元，一方面提高了組合沖突證據能力，另一方面造成了沖突信息的積累，促使分配給主焦元的信度不合理地減小，導致組合信息的不確定性增加，不利于決策。針對DSmT存在的缺陷，提出了一種新的基于沖突再分配的組合規則。為進一步提高DSmT處理沖突、模糊和不精確信息能力，研究了DSmT在直覺模糊集上的拓展，將傳統的信度賦值函數替換為直覺模糊信度賦值映射，并討論了直覺模糊拓展后的信度組合規則。數值實例驗證了所提方法的有效性。

信息融合；DSmT；沖突再分配；直覺模糊集

A

TP391

10.3778/j.issn.1002-8331.1212-0385

TANG Changchun,AO Zhigang,GONG Yunxiang,et al.Improvement of DSm combination rule and its development on intuitionistic fuzzy sets.Computer Engineering and Applications,2014,50（24）：151-155.

江蘇省自然科學基金（No.SBK2009061）。

唐長春（1986—），男，碩士研究生，CCF會員，研究方向：信息融合，軍用數據及知識工程；敖志剛（1959—），男，教授，研究方向：指揮自動化與戰場環境數字化，萬兆以太網；張康益（1988—），男，碩士研究生，研究方向：聯合作戰演練系統分析與集成；王有成（1985—），男，碩士研究生，研究方向：指揮自動化與戰場環境數字化。E-mail：357502975@qq.com

2013-01-04

2013-03-25

1002-8331（2014）24-0151-05

CNKI網絡優先出版：2013-04-09，http∶//www.cnki.net/kcms/detail/11.2127.TP.20130409.1522.002.html

◎圖形圖像處理◎