多重網格在黏性流動最小二乘等幾何模擬中的應用

陳德祥,徐自力

(西安交通大學機械結構強度與振動國家重點實驗室, 710049, 西安)

多重網格在黏性流動最小二乘等幾何模擬中的應用

陳德祥,徐自力

(西安交通大學機械結構強度與振動國家重點實驗室, 710049, 西安)

針對最小二乘等幾何方法模擬黏性流動時條件數大、迭代法收斂速度慢的問題,提出了基于多重網格技術的加速方法。計算中自動生成一系列疏密不同的網格,在最密網格上用最小二乘等幾何方法將Navier-Stokes方程離散為代數方程組,用多重網格方法作為獨立求解器或共軛梯度法的預處理器迭代求解所得到的代數方程組。對雷諾數為100、400、1 000和2 500的頂蓋驅動流進行了數值模擬,計算中進行23次迭代可使方程組的余量降低10個數量級,流動特征量的計算誤差在1%以內。計算結果表明,通過多重網格技術加速迭代,提高了最小二乘等幾何方法模擬黏性流動的計算效率。

多重網格;最小二乘;等幾何方法;共軛梯度法;Navier-Stokes方程

黏性流動現象由Navier-Stokes方程描述,由于非線性導致的復雜性,該方程常用數值方法求解。文獻[1]中對線性的Stokes方程提出了一種最小二乘等幾何方法,用非均勻有理B樣條(NURBS)構造有限元空間,用速度和壓力作為獨立變量,不增加輔助獨立變量。對非線性項進行線性化后,最小二乘等幾何方法可推廣到Navier-Stokes方程的求解[2]。

文獻[1-2]中采用直接方法求解所得的代數方程組,當自由度數增多時直接解法的成本高,需用迭代法求解,這時迭代算法的效率決定了整個程序的計算效率。最小二乘等幾何方法進行流動模擬時,所得到的代數方程條件數大,常用的Richardson型迭代和Krylov子空間型迭代隨著條件數增大收斂速度降低[3],難以滿足要求,因此本文用多重網格技術來提高線性方程組的迭代收斂速度。

多重網格法是目前解代數方程的一種高效迭代算法,Gahalaut等在2013年以泊松方程為對象研究了多重網格在等幾何方法中的應用,結果顯示,提高NURBS階數則多重網格的收斂速度降低[4];劉石等將多重網格與共軛梯度法相結合,改進了采用高階NURBS時的收斂性[5];陳德祥等研究了多重網格在最小二乘等幾何方法中的應用,給出了基于離散B樣條的網格轉換算法[6]。本文根據Navier-Stokes方程的特點對文獻[6]中的多重網格算法進行改進,在此基礎上建立了多重網格共軛梯度法,通過算例對比研究了多重網格作為獨立求解器和作為共軛梯度法的預處理矩陣時的收斂性,最后求解了雷諾數為400、1 000、2 500時的頂蓋驅動流。

1 最小二乘等幾何方法

定常黏性不可壓流動由Navier-Stokes方程描述,其歸一化形式可寫成

-νΔu+u·u+p=f,x∈Ω

(1)

(2)

式中:u為流動速度;p為壓力;f為流體所受到的體積力;ν為流體的黏性系數;Ω為流動區域;x是Ω中的一個點。

式(1)、式(2)分別表示了流動中的動量守恒和質量守恒,求解該方程需要指定合適的定解條件,本文考慮無滑移速度邊界條件和平均壓力條件

u=g,x∈Γ

(3)

(4)

式中:g為邊界上給定的速度;Γ是流動區域的邊界。

采用文獻[2]中的最小二乘等幾何方法進行求解,先用Newton法將控制方程線性化,再對線性化后的方程建立最小二乘變分,最后用NURBS基函數構造有限維空間將控制方程轉化為代數方程

Ax=b

(5)

2 基于多重網格技術的代數方程求解

2.1 多重網格算法

多重網格的基本思想是:在密網格上進行光順,去掉高頻誤差;在疏網格上進行誤差修正,去掉低頻誤差。在迭代中需要使用疏密不同的多組網格,并在不同網格之間進行轉換。對基于NURBS的等幾何方法不同尺寸的網格可在計算中用節點插入算法自動生成,不需要事先準備網格,網格轉換算子可通過離散B樣條得到[6]。由于文獻[6]的算法是由較為簡單的單變量泊松方程給出,要將其用于Navier-Stokes方程還需在以下2方面進行改進。

首先是建立向量值函數的網格轉換算子。以二維問題為例,由于本文基于最小二乘方法,可采用相同的有限維空間近似3個獨立變量,將代數方程中的未知量寫成如下分塊形式

(6)

式中:x1、x2、x3分別是離散后x、y方向的速度以及壓力。

對每一個獨立變量按文獻[6]建立插值算子P′,即對i=1,2,3得

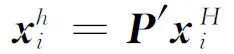
(7)

式中:h、H分別表示密網格和疏網格下的量。因此,總體向量的插值算子為

(8)

根據Galerkin條件可得限制算子為R=PT

(9)

其次是如何滿足平均壓力為零的約束條件。理論上可以通過指定某個參考點壓力值代替約束條件,但這種處理方法會嚴重降低多重網格迭代的收斂性,主要原因是在參考點處誤差光順效果降低。Brandt指出:不必在密網格上處理這種約束條件,只需將約束條件的余量轉換到疏網格上并進行誤差修正即可[7],為此將式(4)離散成如下代數方程

aTx3=0

(10)

如果當前網格為最疏網格(l=1),那么用直接方法求解,對壓力疊加一個常數使它滿足壓力約束條件。如果當前網格不是最疏的(l>1),先進行μ1次光順迭代,通過限制算子將余量轉換到下一層疏網格上(l-1層),并計算壓力約束條件的余量,然后在l-1層調用γ次多重網格算法求解余量方程,最后通過插值算子將修正量轉換到l層,進行μ2次光順迭代。

IFl=1

ELSE

END

2.2 多重網格共軛梯度法

共軛梯度法是一種Krylov子空間迭代方法,它適用于系數矩陣為對稱正定的情況,而基于最小二乘法的系數矩陣總是對稱正定的。理論上若代數方程的維數為n,那么進行n次共軛梯度法迭代將收斂到精確解;實際計算中共軛梯度法的收斂速度快慢取決于所采用的預處理矩陣能否聚集系數矩陣的特征值[3]。多重網格方法也可看成用簡單迭代方法求解某個預處理矩陣作用下的代數方程,這個預處理矩陣能夠有效聚集矩陣特征值。

假設總共k層網格,如果把多重網格迭代看成靜態迭代方法,那么它可寫成如下矩陣形式

(11)

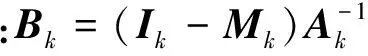
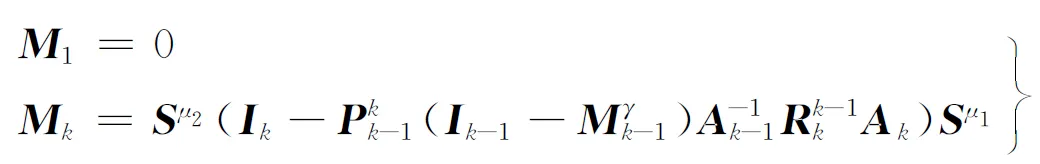
(12)

雖然Bk的表達式包含了Ak的逆矩陣和復雜的遞歸矩陣Mk,無法直接生成,但是它仍然可用作共軛梯度法的預處理矩陣。這是由于共軛梯度法只要求預處理矩陣對稱正定,能快速計算出與任意向量的乘積,并不需要生成預處理矩陣。當μ1=μ2時,采用Jacobi光順或對稱Gauss-Seidel光順的V型和W型多重網格算法都滿足對稱正定要求[9]。由式(11)可知:Bk與任意向量v的乘積Bkv可快速計算出,實際上只要以0向量為初始值,以v為右端項,應用算法1進行一次多重網格迭代即可。算法2是多重網格共軛梯度法偽代碼,它與一般共軛梯度算法的不同是在預處理部分調用了算法1的多重網格迭代。

算法2:MGCG(Ak,bk,x,k,γ,μ1,μ2)

r=bk-Akx

z=MG(Ak,r,0,k,γ,μ1,μ2)

p=z

WHILE not converges

τ=rTz

w=Akp

α=τ/wTp

x=x+αp

r=r-αw

z=MG(Ak,r,0,k,γ,μ1,μ2)

β=rTz/τ

p=z+βp

END

3 數值算例分析

考慮頂蓋驅動流問題,流動區域為單位正方形,兩側及下壁面固定,上壁面的運動速度u=(-1,0)。該問題在文獻中有可信的高精度計算結果[10-12],常作為基準問題用來考核新CFD算法的精確性。本文用Matlab編制了計算程序,分別求解了雷諾數從100到2 500時的流動,并與文獻中的結果進行對比,所有數值結果都是歸一化的。

首先考慮低雷諾數下(Re=100)的流動。多重網格采用5層網格的W型循環,最密網格為32×32,最疏網格為2×2,參數μ1、μ2均取為2,光順算法為對稱Gauss-Seidel迭代。計算中存在嵌套的兩層迭代,外層為Newton迭代,它的收斂條件是相鄰兩次迭代結果的相對誤差小于10-8;內層為線性方程的迭代,它的收斂標準是方程組的余量小于10-10。

圖1表示Re=100時多重網格法(MG)和多重網格共軛梯度法(MGCG)的收斂過程,圖中k是NURBS基函數的連續性指標,從最高點到最低點表示某個Newton迭代步下的線性方程組的收斂過程。對該問題總共需要7次Newton迭代,從圖中可以看出,隨著Newton迭代的推進,線性方程組求解所需的迭代次數逐漸減少。這是因為用前一Newton步的結果作為線性方程組迭代的初始值,隨著Newton迭代的收斂,線性方程組的初始余量也逐漸降低,表現為圖中的高點逐漸減低。比較圖1a、圖1b可以看出:相同k下的MGCG迭代比MG迭代收斂速度快,k=2時,進行23次MGCG迭代方程組的余量降低了10個數量級,k=1時只需14次迭代;當k增大時,MG迭代和MGCG迭代的收斂速度都降低,但是MG迭代的效率降低更多,k從1增大到2,MG所需的迭代次數加倍,而MGCG所需的迭代次數只增加約1/3。

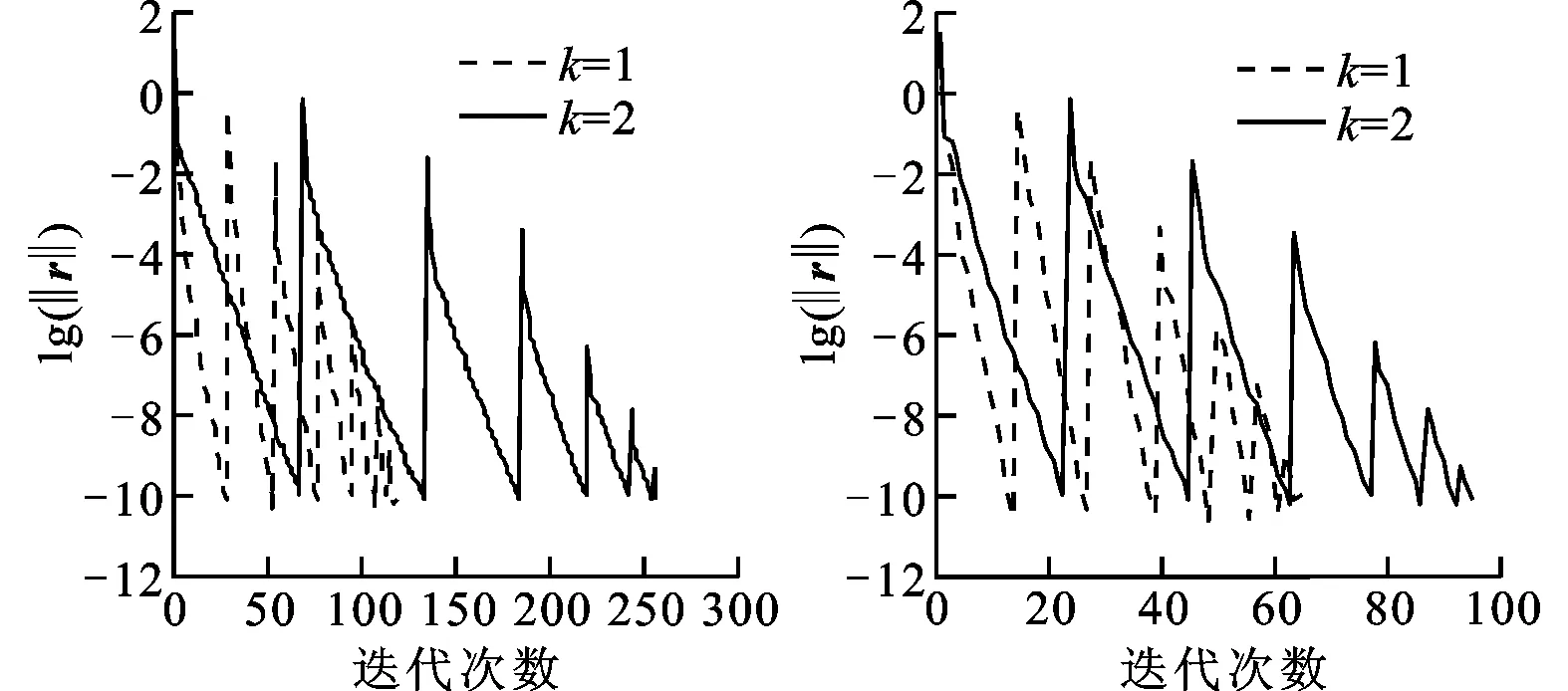
(a)MG算法 (b)MGCG算法

圖2是不同k值下垂直中心線上的x方向速度以及水平中心線上的y方向速度分布,作為對比參照的是Marchi等[10]用1 024×1 024網格得到的結果。本文k=1,2時的總自由度數分別為3 468和3 675,從圖2中可以看出,k=2給出的速度分布更精確,當k值較大時,最小二乘等幾何方法是一種高階方法,網格數不變的條件下,數值解的誤差將隨k的增加呈指數速度下降[1]。

從上面k對多重網格迭代收斂性和解的精度影響分析可知,較大的k值能給出更好的結果,MGCG對k值的敏感性較低,因此基于精度和成本兩方面考慮,計算中k應取較大值,而線性方程組應用MGCG迭代求解。

圖3是Re=10時多重網格共軛梯度法的迭代收斂性過程,k=2、網格數及多重網格參數與前面相同。比較圖3與圖1b可發現,每一個Newton步下Re=10比Re=100需要更多的迭代才能收斂,在文獻[13]中也發現類似的現象,即對最小二乘法在很低雷諾數下用多重網格求解線性方程組不能提高計算效率。這是由于系數矩陣的條件數與雷諾數有關,對最小二乘等幾何方法,Re=10時的條件數大于Re=100時的條件數。

(a)垂直中心線上速度u (b)水平中心線上速度v

圖3 多重網格共軛梯度法收斂過程(Re=10)

對中、高雷諾數流動分別計算了Re=400,1 000,2 500的情況,由于流動的復雜性隨著雷諾數的增加而增加,雷諾數為400、1 000時采用64×64網格,雷諾數為2 500時采用128×128網格。

在雷諾數較大的情況下,用雷諾數遞進技術來解決Newton法收斂半徑小的問題,先以零為初值求解Re=400的流動,再以所得到的結果為初值增大雷諾數進行迭代計算,逐漸遞增到指定的雷諾數。Newton迭代收斂標準是相鄰兩次迭代結果的相對誤差小于10-10,MGCG迭代收斂標準是方程組的余量小于10-8。

取k=6進行計算,圖4是Re=1 000時流函數、渦量和壓力的分布圖,可以看到流動中存在一個主渦,在左、右下角存在兩個次渦,圖中的分布趨勢與文獻[12]給出的分布圖一致。表1和表2分別是主渦和左下角次渦的參數(流函數ψ、渦量ω、渦中心坐標x,y)隨k增大過程中的收斂情況,與文獻[12]中的結果對比可以看出,k=6所得的數值解具有較高的精度,相對誤差在1%以內。

(b)渦量

(c)壓力

表1 主渦的收斂性(Re=1 000)

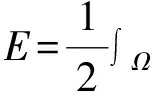
表2 左下角次渦的收斂性(Re=1 000)

表3 全局收斂性(Re=1 000)

圖5和圖6分別是垂直中心線上x方向速度分布和水平中心線上y方向速度分布,其中Marchi等[10]采用了1 024×1 024網格,Erturk等[11]采用了600×600網格,可以看出,對于Re=400,1 000,2 500時本文方法得到的速度分布與文獻中的高精度計算所得結果一致。

圖5 不同雷諾數下垂直中心線上x方向速度分布

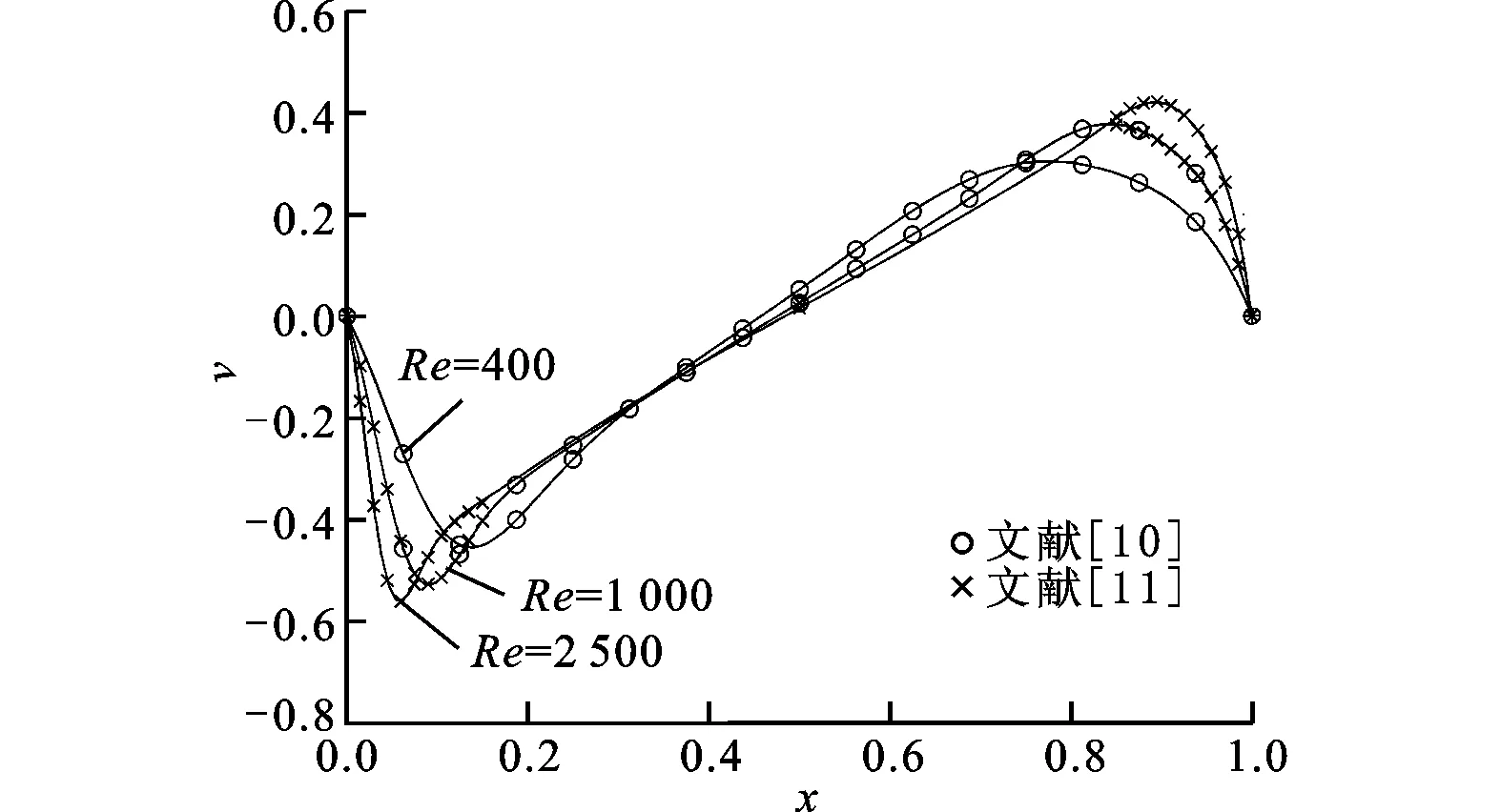
圖6 不同雷諾數下水平中心線上y方向速度分布

4 結 論

多重網格技術提高了最小二乘等幾何方法模擬黏性流動的計算效率。多重網格迭代過程中用密網格使高頻誤差衰減掉,用疏網格使低頻誤差衰減掉,最終線性方程組的余量在迭代中快速衰減,將多重網格法與共軛梯度法相結合進一步提高了迭代收斂速度,進行23次迭代可使方程組的余量降低10個數量級。

流場的計算精度隨NURBS基函數的連續性指標k的增大而提高。對雷諾數為100、400、1 000和2 500的頂蓋驅動流進行了數值模擬,k=6時流動特征量的計算誤差在1%以內,k增大時多重網格共軛梯度法比多重網格法具有更好的收斂性。

[1] 陳德祥, 徐自力, 劉石, 等.求解Stokes方程的最小二乘等幾何分析方法 [J].西安交通大學學報, 2013, 47(5): 51-55.

CHEN Dexiang, XU Zili, LIU Shi, et al.Least squares isogeometric analysis for Stokes equation [J].Journal of Xi’an Jiaotong University, 2013, 47(5): 51-55.

[2] CHEN Dexiang, XU Zili, LIU Shi, et al.Least squares finite element method with high continuity NURBS basis for incompressible Navier-Stokes equations [J].Journal of Computational Physics, 2014, 260: 204-221.

[3] SAAD Y.Iterative methods for sparse linear systems [M].Philadelphia, USA: SIAM, 2003.

[4] GAHALAUT K P S, KRAUS J K, TOMAR S K.Multigrid methods for isogeometric discretization [J].Computer Methods in Applied Mechanics and Engi-neering, 2013, 253: 413-425.

[5] 劉石, 陳德祥, 馮永新, 等.等幾何分析的多重網格共軛梯度法 [J].應用數學和力學, 2014, 25(6): 630-639.

LIU Shi, CHEN Dexiang, FENG Yongxin, et al.A multigrid preconditioned conjugate gradient method for isogeometric analysis [J].Applied Mathematics and Mechanics, 2014, 25(6): 630-639.

[6] 陳德祥, 竇柏通, 徐自力.最小二乘等幾何分析的多重網格方法 [J].西安交通大學學報, 2014, 48(7): 124-130.

CHEN Dexiang, DOU Baitong, XU Zili.Multigrid least squares isogeometric analysis [J].Journal of Xi’an Jiaotong University, 2014, 48(7): 124-130.

[7] BRANDT A, LIVNE O E.Multigrid techniques: 1984 guide with applications to fluid dynamics [M].Philadelphia, USA: SIAM, 2011.

[8] TATEBE O.The multigrid preconditioned conjugate gradient method [C]∥The Sixth Copper Mountain Conference on Multigrid Methods.Copper Mountain, USA: NASA, 1993: 621-634.

[9] TROTTENBERG U, OOSTERLEE C W, SCHULLER A.Multigrid [M].London, UK: Academic Press, 2000: 28-50.

[10]MARCHI C H, SUERO R, ARAKI L K.The lid-driven square cavity flow: numerical solution with a 1 024×1 024 grid [J].Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2009, 31(3): 186-198.

[11]ERTURK E, CORKE T C, GOKCOL C.Numerical solutions of 2D steady incompressible driven cavity flow at high Reynolds numbers [J].International Journal for Numerical Methods in Fluids, 2005, 48(7): 747-774.

[12]BOTELLA O, PEYRET R.Benchmark spectral results on the lid-driven cavity flow [J].Computers & Fluids, 1998, 27(4): 421-433.

[13]RANJAN R, REDDY J N.On multigrid methods for the solution of least-squares finite element models for viscous flows [J].International Journal of Computational Fluid Dynamics, 2012, 26(1): 45-65.

[14]BRUNEAU C H, SAAD M.The 2D lid-driven cavity problem revisited [J].Computers & Fluids, 2006, 35(3): 326-348.

(編輯 趙煒)

AnApplicationofMultigridinViscousFlowSimulationswithLeastSquaresIsogeometricMethod

CHEN Dexiang,XU Zili

(State Key Laboratory for Strength and Vibration of Mechanical Structures, Xi’an Jiaotong University, Xi’an 710049, China)

A multigrid technique to accelerate iteration is proposed to solve the problem of low convergence rate due to large condition number in simulating viscous flow with the least squares isogeometric method.A series of grids with different element sizes are automatically generated in analysis.The least squares isogeometric method is used to discretize the Navier-Stokes equations into a system of linear equations on the densest grid, and the system is iteratively solved using either the multigrid method as standard solver or the preconditioner of the conjugate gradient method.Numerical simulations are performed on lid driven cavity flow withRe=100, 400, 1 000 and 2 500.The residual of algebraic equations is reduced about 10 order of magnitude after 23 iterations, and the calculation error on characteristic parameters of the cavity flow is less than 1%.The results show that the performance of the least squares isogeometric method for viscous flow is improved when the multigrid acceleration technique is used.

multigrid; least squares; isogeometric method; conjugate gradient method; Navier-Stokes equations

2014-05-19。

陳德祥(1979—),男,博士生;徐自力(通信作者),男,教授,博士生導師。

國家“973計劃”資助項目(2011CB706505)。

時間:2014-08-13

10.7652/xjtuxb201411021

O241.82;O357.1

:A

:0253-987X(2014)11-0122-06

網絡出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20140813.1008.003.html