采用星座旋轉(zhuǎn)的高速率空時分組碼空間調(diào)制算法

陳誠,王磊,李曉峰

(西安交通大學電子與信息工程學院, 710049, 西安)

采用星座旋轉(zhuǎn)的高速率空時分組碼空間調(diào)制算法

陳誠,王磊,李曉峰

(西安交通大學電子與信息工程學院, 710049, 西安)

針對空時分組碼空間調(diào)制(STBC-SM)算法中由空間維度調(diào)制所能提供的頻譜效率較低的問題,提出了一種采用星座旋轉(zhuǎn)的高速率空時分組碼空間調(diào)制(CR-STBC-SM)算法。該算法首先從所有有效天線組合中選擇2根天線,然后從M-PSK/QAM星座圖中選擇一組符號對,最后以Alamouti編碼或其對應的星座旋轉(zhuǎn)編碼的形式將符號傳輸出去,并且為了最大化發(fā)射分集增益與編碼增益,進一步對旋轉(zhuǎn)角度進行了優(yōu)化。此外,CR-STBC-SM算法還利用Alamouti碼的正交性來實現(xiàn)低復雜度的最大似然譯碼。仿真結(jié)果表明:與STBC-SM算法相比,在發(fā)射天線數(shù)相同時,CR-STBC-SM算法可以獲得額外0.5 b/(s·Hz)的頻譜效率;當頻譜效率為4 b/(s·Hz)時,2種算法的性能非常接近,但是CR-STBC-SM算法可以節(jié)省3根發(fā)射天線,從而節(jié)約了硬件資源。

空時分組碼;空間調(diào)制;星座旋轉(zhuǎn);發(fā)射分集

在無線通信技術(shù)中,由于空間調(diào)制(SM)和空移鍵控(SSK)可以利用空間維度來傳遞額外的信息,相比于傳統(tǒng)的多輸入多輸出(MIMO)技術(shù)可以獲得更高的頻譜效率,同時SM和SSK還具有對射頻鏈路要求較低、避免信道間干擾(ICI)以及更高的能量效率等優(yōu)勢[1-4],因此近年來作為一種新穎的MIMO傳輸技術(shù)受到了廣泛的關(guān)注[5-7]。然而,SM和SSK在每次傳輸時只能激活一根天線,所以它們不能獲得發(fā)射分集,只能依賴接收分集來對抗信道衰落。

為了提高SM和SSK的發(fā)射分集增益,文獻[8]提出了一種利用脈沖成型技術(shù)的SSK方案(TOSD-SSK),可以取得的發(fā)射分集階數(shù)為2,但是該算法中的脈沖成型的設計比較復雜。文獻[9]提出一種利用天線選擇技術(shù)獲得發(fā)射分集的SSK算法,可以獲得選擇分集增益,但在該算法中,需要接收端反饋信息至發(fā)射端,增加了反饋開銷。文獻[10]利用時間分集的方法使SSK獲得發(fā)射分集增益,但由于采用了時間分集使得SSK的傳輸速率更低了。文獻[11]提出了基于坐標交織的空間調(diào)制算法(CIOD-SM),同樣可以獲得發(fā)射分集增益,然而其系統(tǒng)頻譜效率較低。文獻[12]提出了空時移鍵控(STSK)傳輸方案,通過額外的信息比特來激活不同的散射矩陣,可以獲得的分集階數(shù)為發(fā)射天線數(shù)與傳輸時隙中的最小值。但是,在STSK方案中最優(yōu)的散射矩陣集需要用計算機做最優(yōu)搜索,這使得STSK具有較高的設計復雜度,同時傳輸速率也會隨著時隙數(shù)的增多而線性減小。文獻[13]將SM與空時分組碼(STBC)相結(jié)合提出了一種新的方案,稱為空時分組碼空間調(diào)制(STBC-SM),通過從所有的發(fā)射天線中激活2根天線來發(fā)送Alamouti編碼,Alamouti碼中包含的符號與激活的天線對均攜帶信息,通過優(yōu)化不同碼字之間的旋轉(zhuǎn)角度獲得的發(fā)射分集階數(shù)為2。此外,在接收端利用Alamouti碼的正交性可以實現(xiàn)低復雜度的最大似然(ML)譯碼。然而,STBC-SM方案中由于其設計的碼字數(shù)有限,因此該方案中由空間維度調(diào)制所提供的頻譜效率較低。對此,文獻[14]提出了一種高速率STBC-SM方案(H-STBC-SM),其中采用Alamouti碼作為核心矩陣,通過設計多個空間星座(SC)矩陣與Alamouti矩陣相乘來構(gòu)造空時碼字,將碼字數(shù)擴展為STBC-SM的2倍。但是,H-STBC-SM中設計的碼字僅適合發(fā)射天線數(shù)為4和6的情況,并不適合于其他的天線數(shù)。

本文針對現(xiàn)有的STBC-SM和H-STBC-SM算法的缺陷,提出了通過星座圖旋轉(zhuǎn)的Alamouti碼來擴展碼字數(shù)的空時分組碼空間調(diào)制算法,簡稱為CR-STBC-SM。該算法的主要思想是分別利用Alamouti碼的編碼矩陣及其對應的旋轉(zhuǎn)矩陣來構(gòu)造CR-STBC-SM中的碼字矩陣,因此擴展了碼字數(shù),同時該方案也適合于任意天線數(shù),另一方面,通過對旋轉(zhuǎn)角度的優(yōu)化可以使該方案獲得最大的分集增益和編碼增益。此外,利用Alamouti碼的正交性,該方案在接收端可以實現(xiàn)低復雜度的ML譯碼。

1 系統(tǒng)模型

考慮一個具有Nt根發(fā)射天線和Nr根接收天線的MIMO系統(tǒng)。假設在T個時隙內(nèi)的發(fā)射信號為T×Nt維碼字矩陣X,則T×Nr維的接收信號矩陣可以表示為

Y=ρ1/2XH+N

(1)

式中:ρ是每個接收天線處的平均信噪比(SNR);H和N分別表示Nt×Nr維的信道矩陣和T×Nr維的噪聲矩陣。H和N中的元素均服從均值為0、方差為1的獨立同分布的高斯分布,假設H為準靜態(tài)瑞利衰落信道,在T個時隙內(nèi)保持不變,且只有接收端已知信道狀態(tài)信息。

對于采用STBC-SM調(diào)制的MIMO系統(tǒng),采用的STBC為Alamouti碼,因此T=2,發(fā)送信號X為2×Nt維的矩陣。在Nt=4時,文獻[13]設計的2個子碼本χk,k∈{1,2}為

(2)

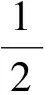
2 CR-STBC-SM算法

針對STBC-SM方案中設計的碼字數(shù)c較小的問題,本文提出一種CR-STBC-SM算法,通過引入星座圖旋轉(zhuǎn)的Alamouti碼來擴展STBC-SM的碼字數(shù),從而提高了系統(tǒng)的頻譜效率。

對于含4根天線的MIMO系統(tǒng),本方案有2個子碼本χk,k∈{1,2},其設計如下

(3)

下面給出CR-STBC-SM算法中碼字的一般設計方法。

圖1 CR-STBC-SM算法發(fā)射端的實現(xiàn)框圖

通過分析可知,本文CR-STBC-SM算法的頻譜效率為

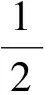
(4)

表1 不同發(fā)射天線數(shù)下3種算法由空間維度調(diào)制所提供的頻譜效率比較

Nt頻譜效率/b·(s·Hz)-1STBC?SMH?STBC?SMCR?STBC?SM30 51 041 01 51 551 52 061 52 02 072 02 582 02 5

從表1可以發(fā)現(xiàn),CR-STBC-SM比STBC-SM算法由空間維度調(diào)制所提供的頻譜效率高0.5b/(s·Hz),在發(fā)射天線數(shù)為4和6時,CR-STBC-SM與H-STBC-SM算法的頻譜效率相同,但CR-STBC-SM算法對于任意發(fā)射天線數(shù)都適應,而非僅僅局限于4、6根發(fā)射天線。

3 CR-STBC-SM系統(tǒng)的參數(shù)優(yōu)化

(5)

Gc1=min det(ΔΔH)=

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

Gc2.1.2,Gc2.2.1,Gc2.2.2,Gc2.2.3,Gc3.1,Gc3.2)

(14)

(15)

4 最大似然檢測算法

對于有c個碼字的CR-STBC-SM算法,當其調(diào)制階數(shù)為M時,可以構(gòu)成cM2個不同的碼字矩陣。CR-STBC-SM算法進行ML譯碼時,需要對cM2個碼字矩陣進行搜索,其譯碼復雜度較高。與文獻[13]類似,利用Alamouti碼的正交性也可以將CR-STBC-SM的ML譯碼簡化為一個線性過程。首先將式(1)簡化為

(16)

式中:Ηχ是與發(fā)送的碼字矩陣相對應的2Nr×2維等價信道矩陣;y和n分別表示2Nr×1維的等價接收信號和噪聲。

對于Nt=4,選擇式(3)中的8個碼字作為發(fā)送的碼字,即式(16)含有8個等價的信道矩陣。式(17)給出了激活天線索引號為(1,2)、(2,3)時系統(tǒng)的等價信道矩陣,對于天線索引號為(3,4)、(4,1)時的等價信道矩陣則與式(17)相似

表2 Nt從3增大到6時最優(yōu)的旋轉(zhuǎn)角度和相應的編碼增益

(17)

5 仿真結(jié)果與分析

為了驗證所提算法的有效性,本節(jié)對STBC-SM、H-STBC-SM以及CR-STBC-SM算法的誤比特(BER)性能進行了仿真,并對仿真結(jié)果進行了分析。

仿真實驗中不同方案的接收天線數(shù)均設為1,圖2給出了在QPSK調(diào)制時,CR-STBC-SM、H-STBC-SM和STBC-SM算法在碼字數(shù)c分別為4和16時,即頻譜效率為3和4 b/(s·Hz)時的BER曲線。當頻譜效率為3 b/(s·Hz)時,CR-STBC-SM需要3根發(fā)射天線,而STBC-SM需要4根發(fā)射天線;當頻譜效率為4 b/(s·Hz)時,CR-STBC-SM、H-STBC-SM和STBC-SM則分別需要5、6、8根發(fā)射天線。由圖2可以看出,幾種不同算法的BER曲線的斜率相同,因而它們獲得了相同的分集增益2Nr。此外,當頻譜效率為4 b/(s·Hz)時,CR-STBC-SM在節(jié)約1根發(fā)射天線的情況下,BER性能仍然略好于H-STBC-SM;在3和4 b/(s·Hz)的頻譜效率下,CR-STBC-SM分別節(jié)省了1根和3根發(fā)射天線,但是卻能和STBC-SM獲得非常相近的BER性能。

圖2 頻譜效率為3、4 b/(s·Hz)時3種算法的BER性能比較

圖3給出了CR-STBC-SM、H-STBC-SM和STBC-SM算法分別采用BPSK和8QAM調(diào)制方式下的BER曲線。由圖3可見,在碼字數(shù)c=8、頻譜效率為2.5b/(s·Hz)、發(fā)射天線數(shù)均為4時,CR-STBC-SM的BER性能與H-STBC-SM非常接近,但是在c=16、頻譜效率為5 b/(s·Hz)、發(fā)射天線數(shù)均為6時,CR-STB-SM獲得了比H-STBC-SM更好的性能。與STBC-SM相比,CR-STBC-SM與其性能相近,但是在相同的頻譜效率下,CR-STBC-SM配置的發(fā)射天線數(shù)比STBC-SM少了2根,因此節(jié)約了硬件資源。

6 結(jié) 論

針對STBC-SM算法由空間維度調(diào)制所提供的頻譜效率較低的問題,本文提出了一種新的改進算法CR-STBC-SM,該算法通過引入星座旋轉(zhuǎn)的Alamouti碼來擴展碼字數(shù),使得系統(tǒng)的頻譜效率得到了有效提高。同時,CR-STBC-SM算法在接收端可以實現(xiàn)低復雜度ML譯碼。理論分析及仿真結(jié)果表明,相比于STBC-SM,在相同頻譜效率下,CR-STBC-SM算法以很小的BER性能損失換來了發(fā)射天線數(shù)的節(jié)約。相比于H-STBC-SM,本文算法在4、5 b/(s·Hz)時獲得了更好的BER性能,而且對于發(fā)射天線數(shù)沒有嚴格的要求,因此靈活性更高。

[1] MEELEH R Y, HASS H, SINANOVIC S, et al. Spatial modulation [J]. IEEE Transactions on Vehicular Technology, 2008, 57(4): 2228-2241.

[2] MALEKI M, BAHRAMI H R, ALIZADEH A, et al. On the performance of spatial modulation: optimal constellation breakdown [J]. IEEE Transactions on Communications, 2014, 62(1): 144-157.

[3] PEPPAS K P, ZAMKOTSIAN M, LAZARAKIS F, et al. Unified error performance analysis of space shift keying modulation for MISO and MIMO systems under generalized fading [J]. IEEE Wireless Communications Letters, 2013, 2(6): 663-666.

[4] LIANG Han-Wen, CHANG R Y, CHUNG Wei-Ho, et al. Bi-space shift keying modulation for MIMO systems [J]. IEEE Communications Letters, 2012, 16(8): 1161-1164.

[5] GESBESRT D, SHAFI M, SHIU D S, et al. From theory to practice: an overview of MIMO space-time coded wire-less systems [J]. IEEE Journal on Selected Areas in Communications, 2003, 21(3): 281-302.

[6] CHEN H H, YEH Y C, GUIZANI M. Space-time complementary coding MIMO with joint spatial diversity and multiplex capability [J]. IEEE Transactions on Wireless Communications, 2008, 7(8): 2950-2956.

[7] WANG Dongming, WANG Jianzhou, YOU Xiaohu, et al. Spectral efficiency of distributed MIMO systems [J]. IEEE Journal on Selected Areas in Communications, 2013, 31(10): 2112-2127.

[8] RENZO M D, HASS H. Space shift keying (SSK-) MIMO over correlated Rician fading channels: performance analysis and a new method for transmit-diversity [J]. IEEE Transactions on Communications, 2011, 59(1): 116-129.

[9] 李曉峰, 王磊, 張曉陽. 獲得天線選擇分集的空移鍵控調(diào)制算法 [J]. 西安交通大學學報, 2013, 47(8): 98-103. LI Xiaofeng, WANG Lei, ZHANG Xiaoyang. A space shift keying modulation for antenna selection diversity [J]. Journal of Xi’an Jiaotong University, 2013, 47(8): 98-103.

[10]YANG Du, XU Chao, YANG Lieliang, et al. Transmit-diversity-assisted space-shift keying for allocated and distributed/cooperative MIMO elements [J]. IEEE Transactions on Vehicular Technology, 2011, 60(6): 2864-2869.

[11]聶仲爾, 王安國, 曲倩倩, 等. 一種采用坐標交織空時編碼的空間調(diào)制方案 [J]. 計算機工程與應用, 2012, 48(20): 103-107. NIE Zhong’er, WANG Anguo, QU Qianqian, et al. Coordinate interleaved space time coded spatial modulation scheme [J]. Journal of Computer Engineering and Application, 2012, 48(20): 103-107.

[12]SUGIURA S, CHEN S, HANZO L. Generalized space time shift keying designed for flexible diversity, multiplexing and complexity tradeoffs [J]. IEEE Transactions on Wireless Communications, 2011, 10(4): 1144-1153.

[13]BASAR E, AYGOLU U, PANAYIRCI E, et al. Space-time block coded spatial modulation [J]. IEEE Transactions on Communications 2011, 59(3): 823-832.

[14]LE M T, NGO V D, MAI H A, et al. High-rate space-time block coded spatial modulation [C]∥Proceeding of IEEE International Conference on Advanced Technologies for Communications. Piscataway, NJ, USA: IEEE, 2012: 278-282.

(編輯 劉楊)

AHighRateSpace-TimeBlockCodingSpatialModulationAlgorithmUsingConstellationRotation

CHEN Cheng,WANG Lei,LI Xiaofeng

(School of Electronics and Information Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

A high rate space-time block coding spatial modulation(STBC-SM) algorithm based on constellation rotation, called CR-STBC-SM, is presented to improve the spectral efficiency of STBC-SM generated by the spatial modulation. The new scheme chooses two antennas from effective antenna combinations, and then a pair of symbols is drawn from the M-PSK/QAM constellation. The symbols are then transmitted in the form of Alamouti code or constellation rotated Alamouti code. The rotation angles are further optimized to maximize the diversity and coding gains of CR-STBC-SM. Moreover, the CR-STBC-SM uses the orthogonality of Alamouti code to get a low-complexity maximum likelihood (ML) decoder. Simulation results and comparison with the STBC-SM scheme show that under the same number of transmit antennas the CR-STBC-SM achieves an extra spectral efficiency of 0.5 b/(s·Hz). Under the spectral efficiency of 4 b/(s·Hz), the performances of both algorithms are very close, but the CR-STBC-SM saves three transmit antennas, that is, the hardware resource is saved by the CR-STBC-SM.

space-time block coding; spatial modulation; constellation rotation; transmit diversity

2014-03-10。

陳誠(1990—),男,碩士生;王磊(通信作者),女,講師,碩士生導師。

國家自然科學基金資助項目(60902045)。

時間:2014-09-22

10.7652/xjtuxb201412018

TN929.5

:A

:0253-987X(2014)12-0113-07

網(wǎng)絡出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20140922.1520.002.html