大型單軸離心振動(dòng)臺(tái)的復(fù)合控制策略

羅中寶,楊志東,陳良,叢大成

(哈爾濱工業(yè)大學(xué)機(jī)電工程學(xué)院, 150001, 哈爾濱)

大型單軸離心振動(dòng)臺(tái)的復(fù)合控制策略

羅中寶,楊志東,陳良,叢大成

(哈爾濱工業(yè)大學(xué)機(jī)電工程學(xué)院, 150001, 哈爾濱)

針對(duì)離心振動(dòng)臺(tái)中輕柔基礎(chǔ)與上平臺(tái)間的動(dòng)態(tài)耦合及各非線(xiàn)性因素使系統(tǒng)性能惡化的問(wèn)題,在傳統(tǒng)伺服控制策略的基礎(chǔ)上提出了一種復(fù)合控制策略。根據(jù)耦合等效模型設(shè)計(jì)幾何解耦控制器,以消除輕柔基礎(chǔ)與上平臺(tái)間的動(dòng)態(tài)耦合;綜合考慮各非線(xiàn)性因素對(duì)系統(tǒng)性能的影響,提出了基于魯棒控制的反饋控制器和基于兩自由度控制的前饋控制器來(lái)保證系統(tǒng)的穩(wěn)定性和控制精度;引入負(fù)載干擾力補(bǔ)償控制器,以減小負(fù)載動(dòng)態(tài)特性變化對(duì)系統(tǒng)性能的影響。仿真結(jié)果表明,經(jīng)前饋、反饋校正和幾何解耦后,離心振動(dòng)臺(tái)的頻寬已提高至250Hz,完全滿(mǎn)足伺服控制策略的頻寬要求。經(jīng)負(fù)載干擾力補(bǔ)償后,在負(fù)載特性劇烈下降階段位置閉環(huán)的超調(diào)量和調(diào)整時(shí)間已減少至未采用補(bǔ)償?shù)?0%,且在負(fù)載特性隨機(jī)波動(dòng)階段位置閉環(huán)的波形失真也得到了顯著改善。

離心振動(dòng)臺(tái);幾何解耦控制器;魯棒控制;兩自由度控制策略

巖土材料的動(dòng)態(tài)特性都具有很強(qiáng)的非線(xiàn)性,這些特性與巖土應(yīng)力密切相關(guān),而離心機(jī)可提供一個(gè)離心加速度場(chǎng)來(lái)補(bǔ)償物理原型的自重應(yīng)力,通過(guò)對(duì)巖土自重應(yīng)力的補(bǔ)償,便可用小比例尺巖土模型來(lái)精確模擬實(shí)際巖土原型在地震激勵(lì)下的響應(yīng)[1-2]。離心振動(dòng)臺(tái)位于離心機(jī)上,這也為其研制帶來(lái)了諸多挑戰(zhàn):①受離心機(jī)裝機(jī)容量的限制,振動(dòng)臺(tái)基礎(chǔ)(吊籃)的質(zhì)量和剛度有限,造成輕柔基礎(chǔ)-液壓動(dòng)力機(jī)構(gòu)-巖土模型間的動(dòng)態(tài)耦合;②受離心振動(dòng)復(fù)合環(huán)境的影響,電液伺服系統(tǒng)核心控制元件——三級(jí)電液伺服閥的動(dòng)態(tài)特性將發(fā)生變化;③實(shí)驗(yàn)時(shí)振動(dòng)臺(tái)上的兩個(gè)高壓蓄能器被作為短時(shí)激振的油源,油液從高壓蓄能器中流出,造成油源壓力的降低;④巖土模型在地震波的激勵(lì)下,其自身的動(dòng)態(tài)特性也發(fā)生改變。簡(jiǎn)單分類(lèi)可將以上4方面挑戰(zhàn)歸結(jié)為如下3個(gè)研究熱點(diǎn):①耦合特性分析、解耦控制問(wèn)題;②非線(xiàn)性因素的抑制問(wèn)題;③負(fù)載干擾力的補(bǔ)償控制問(wèn)題。

耦合特性分析的主要任務(wù)是闡明輕柔基礎(chǔ)、巖土模型對(duì)液壓動(dòng)力機(jī)構(gòu)動(dòng)態(tài)特性的影響;解耦控制問(wèn)題的重點(diǎn)是如何將上平臺(tái)的絕對(duì)運(yùn)動(dòng)參考轉(zhuǎn)化為輕柔基礎(chǔ)與上平臺(tái)間的相對(duì)運(yùn)動(dòng)參考。對(duì)于耦合特性分析問(wèn)題,Conte等詳細(xì)推導(dǎo)了基礎(chǔ)柔性、負(fù)載動(dòng)態(tài)對(duì)振動(dòng)臺(tái)動(dòng)態(tài)特性的影響[3]。作者以離心振動(dòng)臺(tái)為研究對(duì)象,闡述了該振動(dòng)臺(tái)中的耦合特性[4]。對(duì)于解耦控制,普通振動(dòng)臺(tái)并未涉及,該部分是復(fù)合控制策略研究的重點(diǎn)。

非線(xiàn)性因素的抑制問(wèn)題是在綜合考慮各非線(xiàn)性因素的基礎(chǔ)上,提出一種能同時(shí)保證離心振動(dòng)臺(tái)穩(wěn)定性和控制精度的控制策略。一般來(lái)說(shuō),為了減小非線(xiàn)性因素對(duì)振動(dòng)臺(tái)性能的影響,一般采用自適應(yīng)、魯棒控制策略或自適應(yīng)魯棒復(fù)合控制策略。對(duì)于自適應(yīng)控制而言,最具代表性的是由Stoten提出的基于最小控制綜合(minimal control synthesis,MCS)的控制策略。Stoten等針對(duì)日本E-Defense振動(dòng)臺(tái)中存在的非線(xiàn)性、參數(shù)變化等問(wèn)題,提出了一種基于最小控制綜合的前饋?zhàn)钚】刂凭C合算法[5]。Gizatullin等將該最小控制綜合方法推廣至多軸振動(dòng)臺(tái)[6]。與此同時(shí),國(guó)內(nèi)外也有很多成功將魯棒控制策略應(yīng)用于振動(dòng)臺(tái)控制的先例。Cuyper等在傳統(tǒng)離線(xiàn)迭代技術(shù)的基礎(chǔ)上引入基于魯棒控制的實(shí)時(shí)控制器來(lái)提高離線(xiàn)迭代技術(shù)的收斂速度和收斂精度[7]。Vaes等將文獻(xiàn)[7]中的控制方法擴(kuò)展至多軸振動(dòng)臺(tái),也取得了顯著成果[8]。對(duì)于復(fù)合控制策略,Uchiyama等在電動(dòng)振動(dòng)臺(tái)中引入兩自由度控制策略(2-DOF control),其中采用μ綜合方法設(shè)計(jì)了兩自由度控制中的反饋控制器,在前饋補(bǔ)償部分引入自適應(yīng)濾波器來(lái)進(jìn)一步提高振動(dòng)臺(tái)的控制性能[9]。對(duì)于離心振動(dòng)臺(tái)而言,其復(fù)現(xiàn)的是“短時(shí)高頻”的地震波,持續(xù)時(shí)間僅為1s左右,自適應(yīng)控制策略很難做到收斂。因此,本文引入魯棒控制來(lái)設(shè)計(jì)系統(tǒng)的反饋控制器,達(dá)到保證系統(tǒng)穩(wěn)定性的目的;然后引入基于兩自由度控制策略的前饋補(bǔ)償控制技術(shù)進(jìn)一步提高離心振動(dòng)臺(tái)對(duì)高頻參考信號(hào)的復(fù)現(xiàn)能力。

負(fù)載干擾力補(bǔ)償控制的途徑是采用一種控制方法來(lái)減小負(fù)載動(dòng)態(tài)特性變化對(duì)系統(tǒng)性能的惡化。Iwasaki等針對(duì)非線(xiàn)性試件提出了一種基于干擾力觀測(cè)器的反力補(bǔ)償機(jī)制,經(jīng)驗(yàn)證明該方法可顯著提高振動(dòng)臺(tái)對(duì)地震波的復(fù)現(xiàn)精度[10]。Uchiyama等將該反力補(bǔ)償機(jī)制應(yīng)用于負(fù)載為裝水容器的電動(dòng)振動(dòng)臺(tái)中[11]。本文將負(fù)載力干擾力補(bǔ)償控制引入到離心振動(dòng)臺(tái)中,用以提高振動(dòng)臺(tái)對(duì)巖土模型動(dòng)態(tài)特性變化的抵抗能力。

1 單軸離心振動(dòng)臺(tái)簡(jiǎn)介

圖1所示為哈爾濱工業(yè)大學(xué)與中國(guó)地震局工程力學(xué)研究所聯(lián)合研制的單軸離心振動(dòng)臺(tái)。該單軸離心振動(dòng)臺(tái)的最大振動(dòng)負(fù)載為1350kg,最大振幅為12 mm,最大水平加速度為30g,最大振動(dòng)頻率為350Hz。與普通振動(dòng)臺(tái)、小型離心振動(dòng)臺(tái)相比,該單軸離心振動(dòng)臺(tái)在結(jié)構(gòu)上做出了如下4點(diǎn)創(chuàng)新和嘗試。

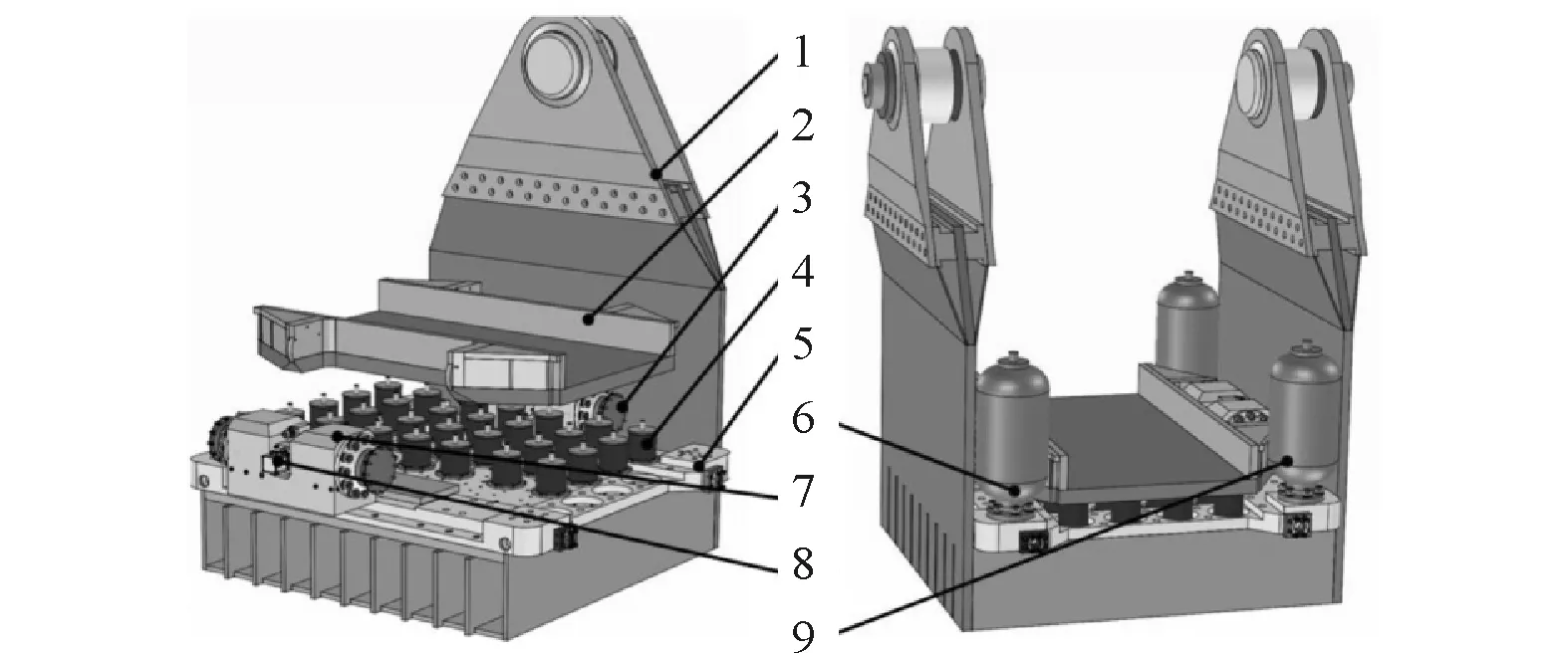
1:吊籃;2:上平臺(tái);3:凹形運(yùn)動(dòng)塊;4:橡膠支撐;5:支撐板;6:高壓蓄能器;7:液壓作動(dòng)器;8:三級(jí)電液伺服閾;9:低壓蓄能器

(1)單軸離心振動(dòng)臺(tái)采用了新型的冗余驅(qū)動(dòng)技術(shù),即由兩套液壓動(dòng)力機(jī)構(gòu)協(xié)同完成離心振動(dòng)臺(tái)的水平單向激振;考慮到結(jié)構(gòu)的緊湊性,每套液壓動(dòng)力機(jī)構(gòu)均由兩條柱塞缸和一臺(tái)三級(jí)伺服閥組成。

(2)普通振動(dòng)臺(tái)、小型離心振動(dòng)臺(tái)的上平臺(tái)與液壓作動(dòng)器間的連接多采用球鉸。考慮到鉸軸的柔性和鉸中存在的間隙,傳統(tǒng)連接方式并不能滿(mǎn)足高頻振動(dòng)的要求。因此,在液壓缸與上平臺(tái)間添加了凹形運(yùn)動(dòng)塊,這種連接方式可在提高連接剛度的同時(shí)減小連接間隙。

(3)支撐導(dǎo)向裝置既要支撐平臺(tái)和巖土模型的高離心力,又要引導(dǎo)它們?cè)谥付ǚ较蛏蠈?shí)現(xiàn)高加速度運(yùn)動(dòng)。單軸離心振動(dòng)臺(tái)在支撐板與上平臺(tái)間安裝了28個(gè)橡膠剪切軸承,用以支撐負(fù)載、平臺(tái)的離心載荷;在水平激振過(guò)程中橡膠軸承發(fā)生水平向的彈性變形,分析時(shí)可將其作為彈性負(fù)載考慮。

(4)圖1中的吊籃即為離心振動(dòng)臺(tái)的反力基礎(chǔ),受離心機(jī)容量的限制,吊籃底座的內(nèi)部做成中空柵格狀,最大限度地減小了吊籃的質(zhì)量,其彈簧剛度也相當(dāng)有限。普通振動(dòng)臺(tái)的反力基礎(chǔ)質(zhì)量一般在負(fù)載、平臺(tái)質(zhì)量和的15倍以上,單軸離心振動(dòng)臺(tái)的該比值不足4∶1。因此,反力基礎(chǔ)的動(dòng)態(tài)特性將會(huì)對(duì)離心振動(dòng)臺(tái)性能產(chǎn)生較大影響。

2 單軸離心振動(dòng)臺(tái)中的關(guān)鍵問(wèn)題

2.1 輕柔基礎(chǔ)-動(dòng)力機(jī)構(gòu)-巖土模型的耦合問(wèn)題

單軸離心振動(dòng)臺(tái)的伺服控制策略是通過(guò)位置閉環(huán)控制來(lái)保證上平臺(tái)的加速度復(fù)現(xiàn)精度,而離心振動(dòng)臺(tái)中位移傳感器反饋的卻是上平臺(tái)、輕柔基礎(chǔ)間的相對(duì)位移,因此,控制時(shí)需將上平臺(tái)絕對(duì)運(yùn)動(dòng)參考轉(zhuǎn)化為上平臺(tái)、輕柔基礎(chǔ)間的相對(duì)運(yùn)動(dòng)參考,其轉(zhuǎn)換關(guān)系依賴(lài)于輕柔基礎(chǔ)-液壓動(dòng)力機(jī)構(gòu)-巖土模型間的動(dòng)態(tài)耦合關(guān)系。本文修正了文獻(xiàn)[4]中的耦合等效模型,主要是將輕柔基礎(chǔ)與上平臺(tái)的耦合劃為運(yùn)動(dòng)學(xué)耦合和動(dòng)力學(xué)耦合。如圖2所示,②中的杠桿表示了上平臺(tái)與輕柔基礎(chǔ)間的運(yùn)動(dòng)學(xué)耦合,杠桿的比率等于有效負(fù)載(上平臺(tái)與負(fù)載)與輕柔基礎(chǔ)的質(zhì)量比;另外,采用①中的一維質(zhì)量-彈簧-阻尼系統(tǒng)來(lái)等效輕柔基礎(chǔ)的動(dòng)態(tài)特性。最終,在文獻(xiàn)[4]的基礎(chǔ)上還考慮了橡膠軸承剛度對(duì)系統(tǒng)耦合特性的影響。經(jīng)推導(dǎo),上平臺(tái)、輕柔基礎(chǔ)間的相對(duì)位移y與伺服閥閥芯位移xv的傳遞函數(shù)

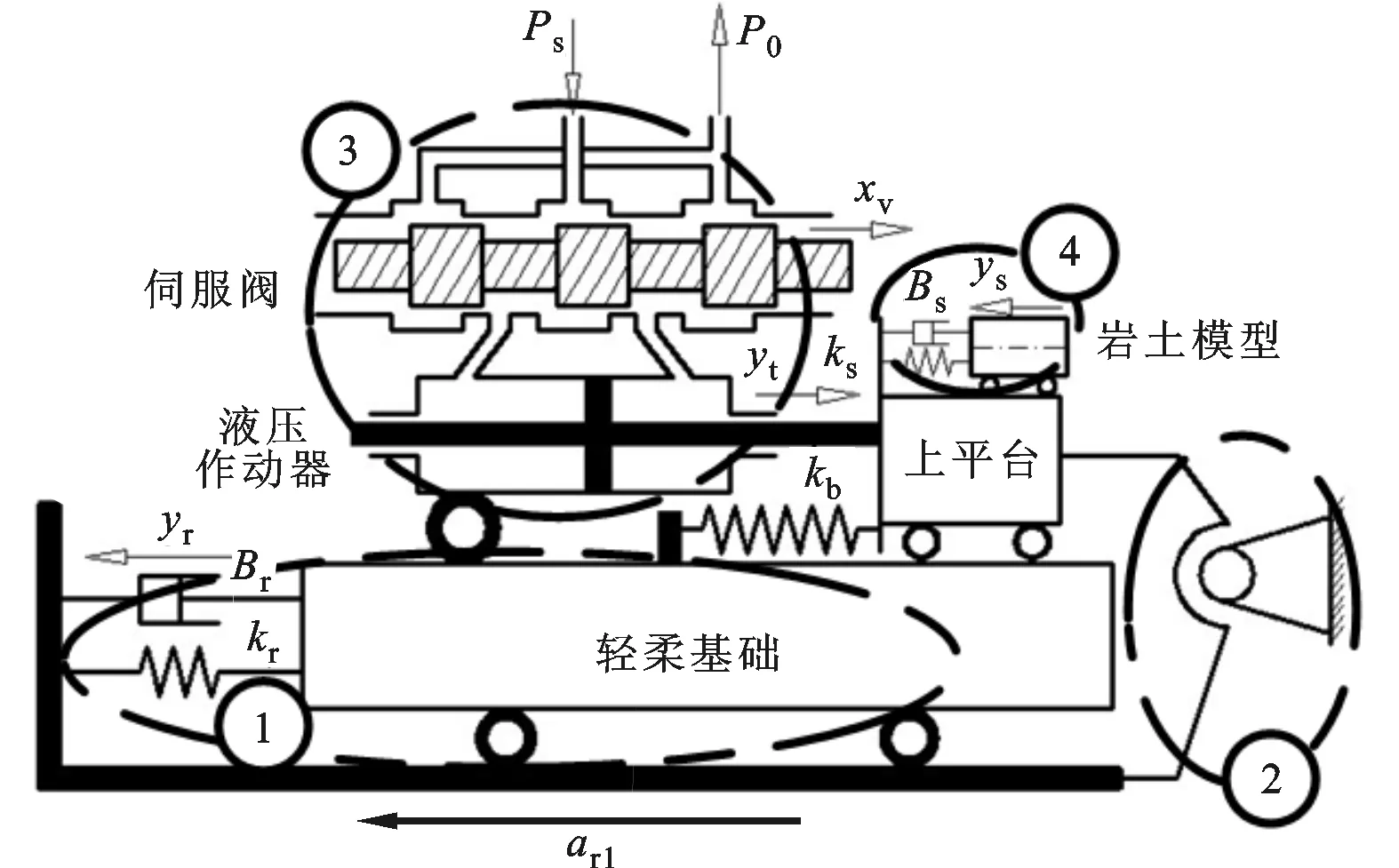
①:輕柔基礎(chǔ)與上平臺(tái)的動(dòng)力學(xué)耦合;②:輕柔基礎(chǔ)與上平臺(tái)的運(yùn)動(dòng)學(xué)耦合;③:液壓動(dòng)力機(jī)構(gòu)的動(dòng)態(tài)特性;④:巖土模型的動(dòng)態(tài)特性

Gyxv=

(1)

W″(s)=

W′(s)=

式中:kq表示伺服閥的流量增益;kce表示總的流量-壓力系數(shù);kb表示橡膠軸承的彈簧剛度;Ap表示液壓缸的有效作用面積;ωs、ξs分別表示巖土模型的固有頻率和阻尼比;ωr1、ξr1分別表示輕柔基礎(chǔ)的綜合固有頻率和阻尼比;其他參數(shù)均由輕柔基礎(chǔ)、液壓動(dòng)力機(jī)構(gòu)、橡膠軸承綜合確定。

2.2 離心振動(dòng)復(fù)合環(huán)境對(duì)三級(jí)伺服閥的影響問(wèn)題

目前,對(duì)三級(jí)伺服閥在離心力振動(dòng)復(fù)合環(huán)境下的特性分析研究幾乎處于空白,但關(guān)于兩級(jí)伺服閥在離心力環(huán)境下的特性分析經(jīng)驗(yàn)值得借鑒。賀云波等根據(jù)伯努利方程、流體沖量定理、力矩馬達(dá)的力矩方程、噴嘴擋板的流量方程、擋板和二級(jí)閥芯的力平衡方程等,分析了伺服閥輸入電流與閥芯位移間的關(guān)系[12]。與之相比,三級(jí)電液伺服閥在復(fù)合環(huán)境下的特性分析較上述研究要復(fù)雜得多,主要表現(xiàn)為:①三級(jí)伺服閥固定于輕柔基礎(chǔ)上,而輕柔基礎(chǔ)的運(yùn)動(dòng)又與2.1節(jié)中的耦合特性相關(guān),因此垂臂安裝時(shí)三級(jí)伺服閥除了在垂直于閥芯方向上受離心力的影響外,還在閥芯方向上受一個(gè)交變的振動(dòng)載荷;②相比兩級(jí)伺服閥,三級(jí)伺服閥加入了第三級(jí)功率級(jí)滑閥,結(jié)構(gòu)的增加使三級(jí)伺服閥在復(fù)合環(huán)境下的特性分析變得更加復(fù)雜。鑒于以上兩點(diǎn),可推斷從理論上研究該問(wèn)題是較為困難的。因此,作者準(zhǔn)備在振動(dòng)臺(tái)的后續(xù)調(diào)試試驗(yàn)中,實(shí)地測(cè)試三級(jí)電液伺服閥在極限復(fù)合環(huán)境下的響應(yīng),從而確定出伺服閥動(dòng)態(tài)特性的攝動(dòng)范圍。

2.3 非線(xiàn)性因素對(duì)振動(dòng)臺(tái)性能的影響問(wèn)題

非線(xiàn)性因素主要包括以下4類(lèi):①蓄能器的非線(xiàn)性;②巖土模型的非線(xiàn)性;③橡膠軸承的非線(xiàn)性;④動(dòng)力機(jī)構(gòu)的非線(xiàn)性。下面將逐一介紹上述因素。

2.3.1 蓄能器的非線(xiàn)性 由于液壓滑環(huán)對(duì)傳輸流量的限制,單軸離心振動(dòng)臺(tái)很難通過(guò)地面油源實(shí)時(shí)供油,因此,振動(dòng)臺(tái)上的高壓蓄能器被作為短時(shí)高頻激振的油源,在激振過(guò)程中油液從高壓蓄能器中持續(xù)流出,從而造成其出口壓力的降低,即油源壓力降低。從控制角度來(lái)講,油源壓力的降低將會(huì)造成流量增益的減小,從而降低系統(tǒng)的頻寬和跟蹤精度。

2.3.2 巖土模型的非線(xiàn)性 巖土模型的動(dòng)態(tài)特性在整個(gè)激振過(guò)程中持續(xù)變化,進(jìn)一步增加了系統(tǒng)的非線(xiàn)性。巖土模型動(dòng)態(tài)特性的變化將會(huì)改變耦合傳遞函數(shù)的反諧振峰,也就改變了離心振動(dòng)臺(tái)位置閉環(huán)系統(tǒng)的主導(dǎo)零點(diǎn),而在振動(dòng)臺(tái)的伺服控制策略中,一般會(huì)加入前饋控制器來(lái)對(duì)消系統(tǒng)頻寬范圍內(nèi)的主導(dǎo)零極點(diǎn),零極點(diǎn)位置的改變將會(huì)使前饋補(bǔ)償失效,從而在一定程度上降低系統(tǒng)的性能。

2.3.3 橡膠軸承的非線(xiàn)性 目前作者已對(duì)單軸離心振動(dòng)臺(tái)的試驗(yàn)樣機(jī)進(jìn)行了一系列驗(yàn)證性試驗(yàn),試驗(yàn)中暴露出橡膠軸承的非線(xiàn)性彈性變形將嚴(yán)重影響振動(dòng)臺(tái)對(duì)加速度波形的復(fù)現(xiàn)精度。除此之外,橡膠軸承的彈簧剛度既會(huì)影響耦合傳遞函數(shù)的開(kāi)環(huán)增益,又會(huì)影響式(1)中慣性環(huán)節(jié)的轉(zhuǎn)折頻率ωb,因此橡膠軸承非線(xiàn)性對(duì)系統(tǒng)的跟蹤精度和頻寬都有較大影響。

2.3.4 動(dòng)力機(jī)構(gòu)的非線(xiàn)性 在線(xiàn)性耦合特性的推導(dǎo)過(guò)程中,同時(shí)對(duì)流量方程、流量連續(xù)性方程進(jìn)行了線(xiàn)性化處理。在推導(dǎo)伺服閥的線(xiàn)性化流量方程時(shí),選用的是負(fù)載流量QL、xv、負(fù)載壓降PL均為0的工作點(diǎn),此時(shí)伺服閥的流量增益最大,從穩(wěn)定性角度考慮這是一種相對(duì)保守的線(xiàn)性化方法。在簡(jiǎn)化流量連續(xù)性方程時(shí),假定活塞初始處于中間位置,此時(shí)執(zhí)行機(jī)構(gòu)的液壓固有頻率最低,系統(tǒng)特性最為保守。在實(shí)際情況下,由于PL、 活塞位置的變化范圍都較大,需考慮液壓動(dòng)力機(jī)構(gòu)非線(xiàn)性對(duì)系統(tǒng)性能的影響。

3 單軸離心振動(dòng)臺(tái)中的復(fù)合控制策略

3.1 復(fù)合控制策略概述

普通振動(dòng)臺(tái)的伺服控制策略包括前置濾波器、三狀態(tài)控制器(包含三狀態(tài)反饋和三狀態(tài)前饋)、自由度控制器(包含自由度分解和自由度合成矩陣)、壓力鎮(zhèn)定控制器、速度合成控制器等,各部分的具體功能及設(shè)計(jì)方法在文獻(xiàn)[4]中都有闡述。如圖3所示,本文提出的復(fù)合控制策略是在傳統(tǒng)伺服控制策略的基礎(chǔ)上做了以下3方面補(bǔ)充:①引入幾何解耦控制器,將上平臺(tái)的絕對(duì)位移參考轉(zhuǎn)化為上平臺(tái)與輕柔基礎(chǔ)間的相對(duì)位移參考,解決輕柔基礎(chǔ)與上平臺(tái)間的耦合問(wèn)題;②引入魯棒控制策略和兩自由度控制策略,在保證系統(tǒng)穩(wěn)定性的前提下提高系統(tǒng)性能;③引入負(fù)載干擾力補(bǔ)償控制器,抑制負(fù)載動(dòng)態(tài)特性變化對(duì)系統(tǒng)性能的影響。下面將詳細(xì)敘述各補(bǔ)充部分的工作原理及設(shè)計(jì)過(guò)程。為簡(jiǎn)化設(shè)計(jì)過(guò)程,假設(shè)引入自由度控制和壓力鎮(zhèn)定控制器已基本解決了兩套作動(dòng)器間的內(nèi)力耦合,因此在后續(xù)研究中將忽略作動(dòng)器間的內(nèi)力耦合,此時(shí)單軸離心振動(dòng)臺(tái)的動(dòng)態(tài)特性可近似等效為單液壓動(dòng)力機(jī)構(gòu)的動(dòng)態(tài)特性。

3.2 幾何解耦控制器

根據(jù)圖2中的等效模型可推導(dǎo)出上平臺(tái)、輕柔基礎(chǔ)相對(duì)位移y到上平臺(tái)絕對(duì)位移yt的傳遞函數(shù),可表示為

(2)

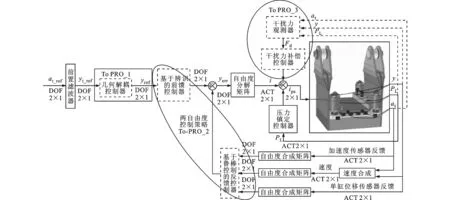
圖3 離心振動(dòng)臺(tái)的復(fù)合伺服控制策略

K=mr/(mt+ms+mr)

ωrb=((kr+kb)/mr)1/2

ξrb=(Br/2)(1/(mrkr+mrkb))1/2ωrts=

((mt+ms+mr)kr/mr)1/2

式中:mr、mt、ms分別代表輕柔基礎(chǔ)、上平臺(tái)、巖土模型的質(zhì)量;kb、kr表示橡膠軸承和輕柔基礎(chǔ)的彈簧剛度;Br表示輕柔基礎(chǔ)的阻尼系數(shù);ar、at表示在輕柔基礎(chǔ)、上平臺(tái)相應(yīng)位置處的加速度。由式(2)可知,該耦合關(guān)系既與各部分質(zhì)量有關(guān),又受到橡膠軸承剛度、輕柔基礎(chǔ)動(dòng)態(tài)特性的影響。由于該單軸離心振動(dòng)臺(tái)已分別在輕柔基礎(chǔ)、上平臺(tái)上的對(duì)應(yīng)位置安裝了加速度傳感器,因此可實(shí)時(shí)測(cè)量輕柔基礎(chǔ)的加速度ar和上平臺(tái)的加速度at。根據(jù)加速度傳感器的測(cè)量結(jié)果和式(2)給出的傳遞函數(shù)形式,便可以辨識(shí)出該耦合關(guān)系的具體參數(shù)。最終,將Gyty的逆作為幾何解耦控制器,用以將上平臺(tái)的絕對(duì)運(yùn)動(dòng)參考轉(zhuǎn)化成上平臺(tái)、輕柔基礎(chǔ)間的相對(duì)運(yùn)動(dòng)參考。

3.3 基于魯棒控制的反饋控制器

如圖4所示,作者借助系統(tǒng)方框圖從以下6方面來(lái)說(shuō)明各非線(xiàn)性因素對(duì)液壓動(dòng)力機(jī)構(gòu)動(dòng)態(tài)特性所產(chǎn)生的影響:①離心振動(dòng)復(fù)合環(huán)境將會(huì)影響三級(jí)電液伺服閥的傳遞函數(shù)Gsv;②高壓油從振動(dòng)臺(tái)中的高壓蓄能器中持續(xù)流出造成油源壓力的持續(xù)降低,油源壓力降低將會(huì)減小伺服閥的流量增益kq;③在流量方程的線(xiàn)性化過(guò)程中,計(jì)算的流量增益kq是假設(shè)負(fù)載壓降PL=0得到的,而實(shí)際過(guò)程PL的變化范圍較大,這也會(huì)對(duì)伺服閥的流量增益kq產(chǎn)生影響;④在流量連續(xù)性方程的推導(dǎo)中,假設(shè)活塞的初始位置位于中間位置,此時(shí)的液壓固有頻率最小,而在實(shí)際情況下,初始位置不一定處于中位及油源壓力的降低也會(huì)對(duì)壓縮泄露流量到負(fù)載壓降的傳遞函數(shù)GQPL產(chǎn)生影響;⑤橡膠軸承的非線(xiàn)性將會(huì)影響其彈簧剛度kb,其彈性曲線(xiàn)可通過(guò)預(yù)先的靜力加載試驗(yàn)測(cè)量獲得;⑥巖土模型動(dòng)態(tài)特性的變化將會(huì)影響巖土模型自身的傳遞函數(shù)。

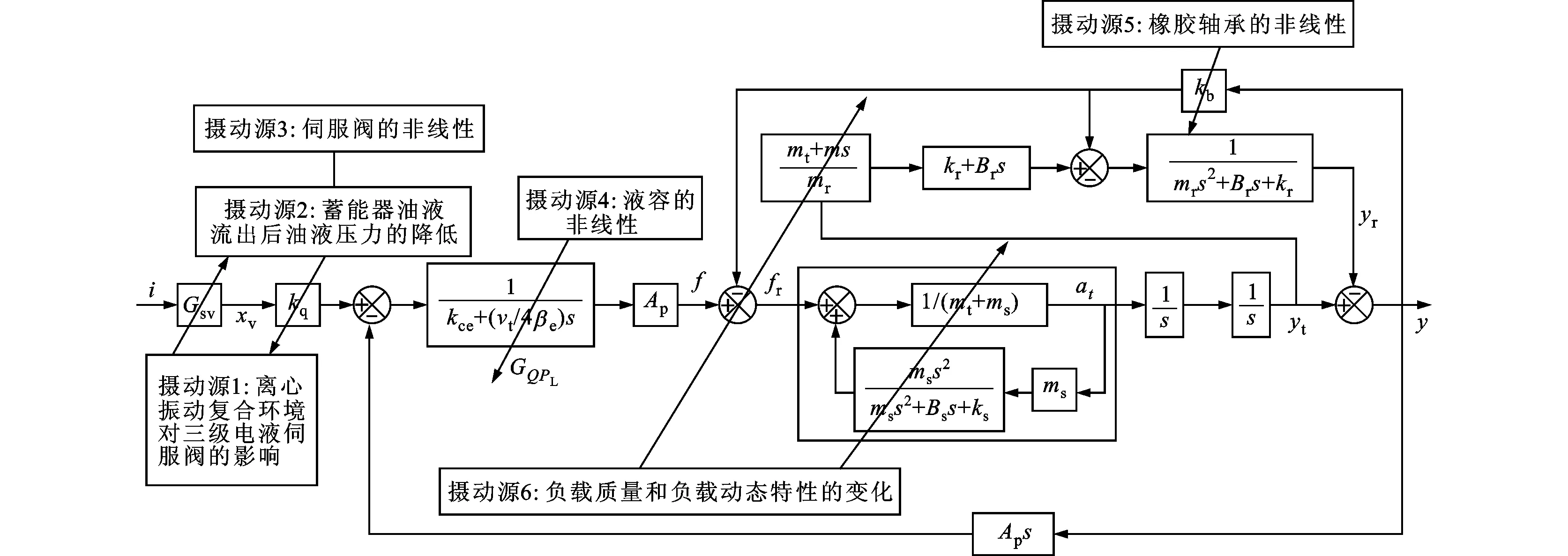
圖4 離心振動(dòng)臺(tái)的傳遞函數(shù)框圖及各攝動(dòng)源對(duì)框圖各部分的影響

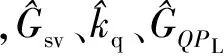
3.4 基于兩自由度控制策略的前饋控制器

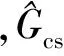
①:液壓缸出力到基礎(chǔ)位移;②:液壓缸出力到上平臺(tái)位移;③:性能權(quán)重的等效表示

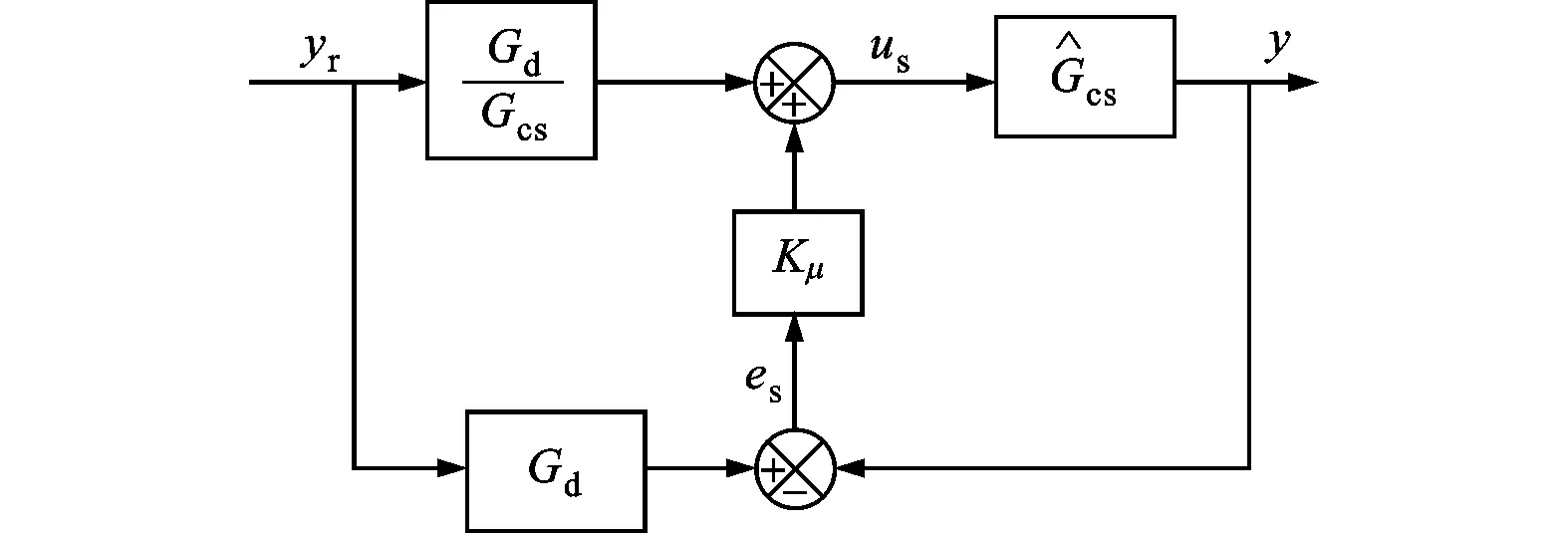
圖6 兩自由度控制策略的方框圖

(3)

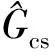
3.5 負(fù)載干擾力補(bǔ)償控制器

如圖7所示,負(fù)載干擾力Fd可表示為

(4)

式中:yr、yt、ys分別表示輕柔基礎(chǔ)、上平臺(tái)的絕對(duì)位移和巖土模型與上平臺(tái)間的相對(duì)位移;kb(y)表示橡膠軸承的彈性曲線(xiàn)。液壓作動(dòng)器兩腔都安裝了壓力傳感器,上平臺(tái)的絕對(duì)加速度、上平臺(tái)與輕柔基礎(chǔ)間的相對(duì)位移也都可由加速度、位移傳感器測(cè)得,再結(jié)合預(yù)先測(cè)得的橡膠軸承的彈性曲線(xiàn),在理論上可實(shí)時(shí)準(zhǔn)確估計(jì)負(fù)載干擾力的值。本文將式(4)的功能定義為干擾力觀測(cè)器。

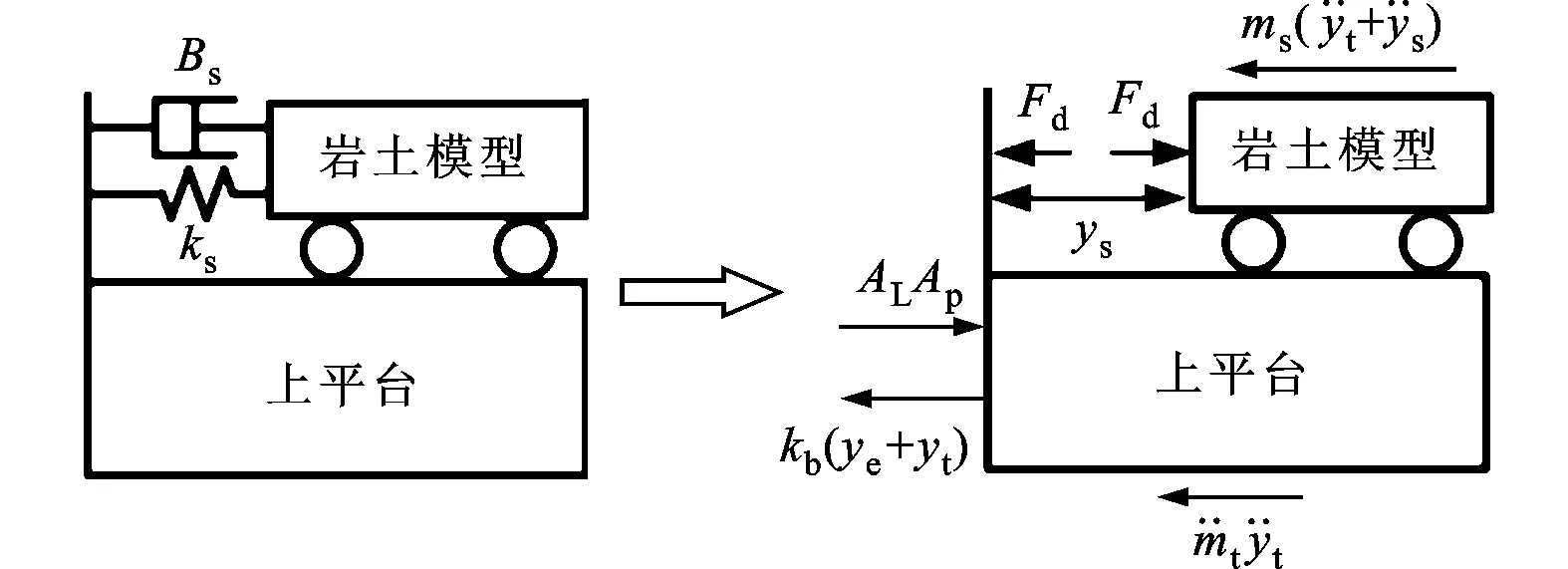
圖7 負(fù)載干擾力的定義

另外,在獲得負(fù)載干擾力的估計(jì)值后,需根據(jù)估計(jì)的負(fù)載干擾力Fd計(jì)算添加到伺服閥上的補(bǔ)償電流iD,本文將這部分命名為干擾力補(bǔ)償器。根據(jù)負(fù)載干擾力Fd的定義修正圖4中的方框圖,結(jié)果如圖8所示(用圖8中標(biāo)記為②的部分替換掉標(biāo)記為①的部分)。參考圖8,經(jīng)簡(jiǎn)單推導(dǎo),當(dāng)補(bǔ)償電流iD滿(mǎn)足式(5)所示的關(guān)系式時(shí),即

iD=Fd(kce+vt/4βes)/GsvkqAp

(5)

此時(shí)傳感器位移輸出y與Fd無(wú)關(guān),說(shuō)明伺服閥補(bǔ)償電流iD在理論上完全消除了負(fù)載干擾力Fd對(duì)系統(tǒng)性能的影響。但是,考慮到系統(tǒng)的非線(xiàn)性,干擾力補(bǔ)償器中的參數(shù)僅是針對(duì)系統(tǒng)的名義模型而設(shè)計(jì)的,因此在實(shí)際情況下補(bǔ)償電流iD只能部分抵消負(fù)載干擾力Fd,并不能完全消除負(fù)載動(dòng)態(tài)特性對(duì)系統(tǒng)性能的影響。為了確保攝動(dòng)情況下負(fù)載干擾力補(bǔ)償控制的穩(wěn)定性,圖中在干擾力補(bǔ)償器前端加入比例增益klcd,調(diào)試時(shí)需將klcd從0逐步增加至1。

圖8 負(fù)載力干擾力補(bǔ)償控制器的原理圖

4 仿真研究

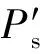
利用Matlab工具箱采用D-K迭代求解如圖5所示的μ綜合問(wèn)題。經(jīng)20次迭代,系統(tǒng)的結(jié)構(gòu)奇異值逐步降至1以下,此時(shí)控制器Kμ的階次為42階。此后,采用基于Hankel奇異值的乘法誤差模型對(duì)魯棒控制器降階,且將降階后的魯棒控制器轉(zhuǎn)換成零極點(diǎn)模型形式,并剔除頻寬范圍以外的零極點(diǎn),得到控制器的最終形式為

(6)

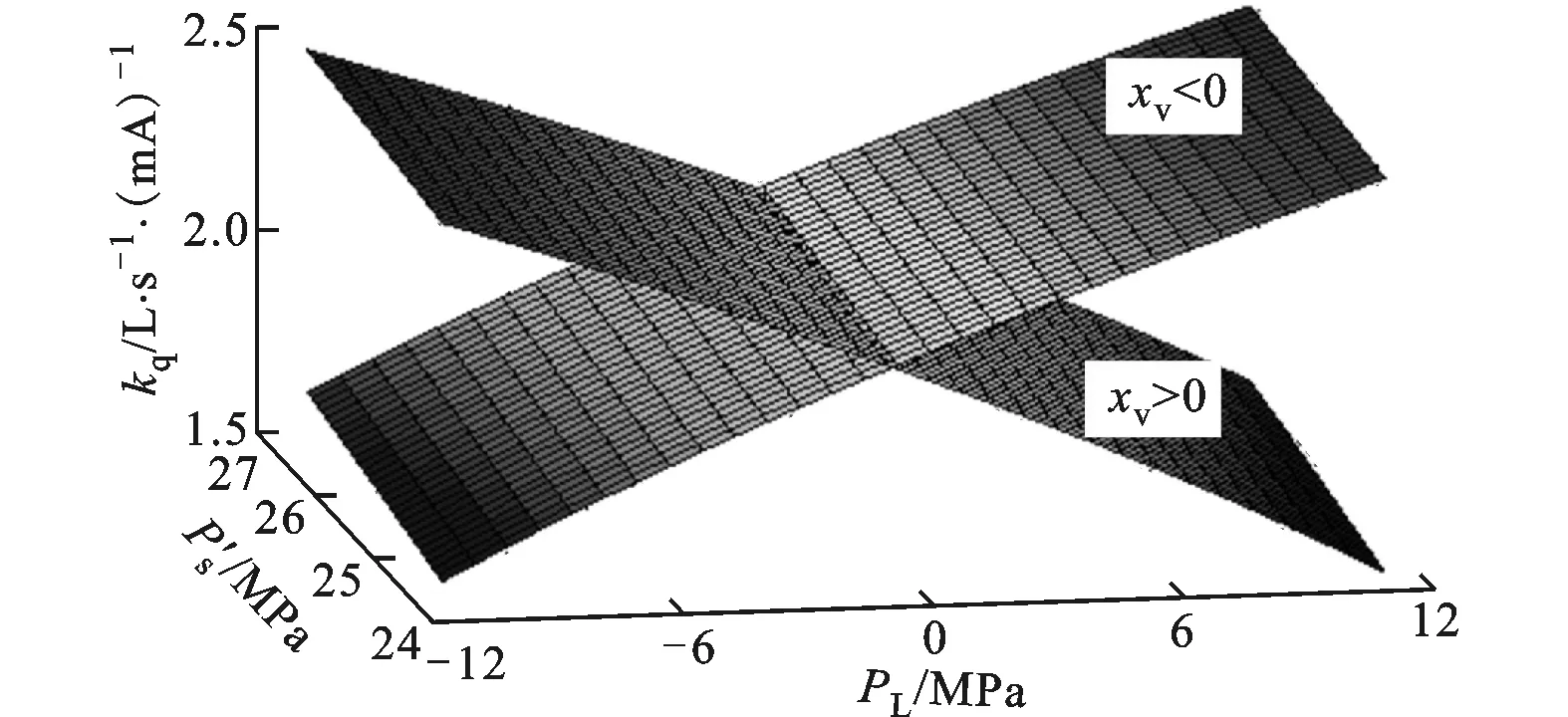
(a)流量增益kq與負(fù)載壓降PL、油源瞬時(shí)應(yīng)力間的關(guān)系

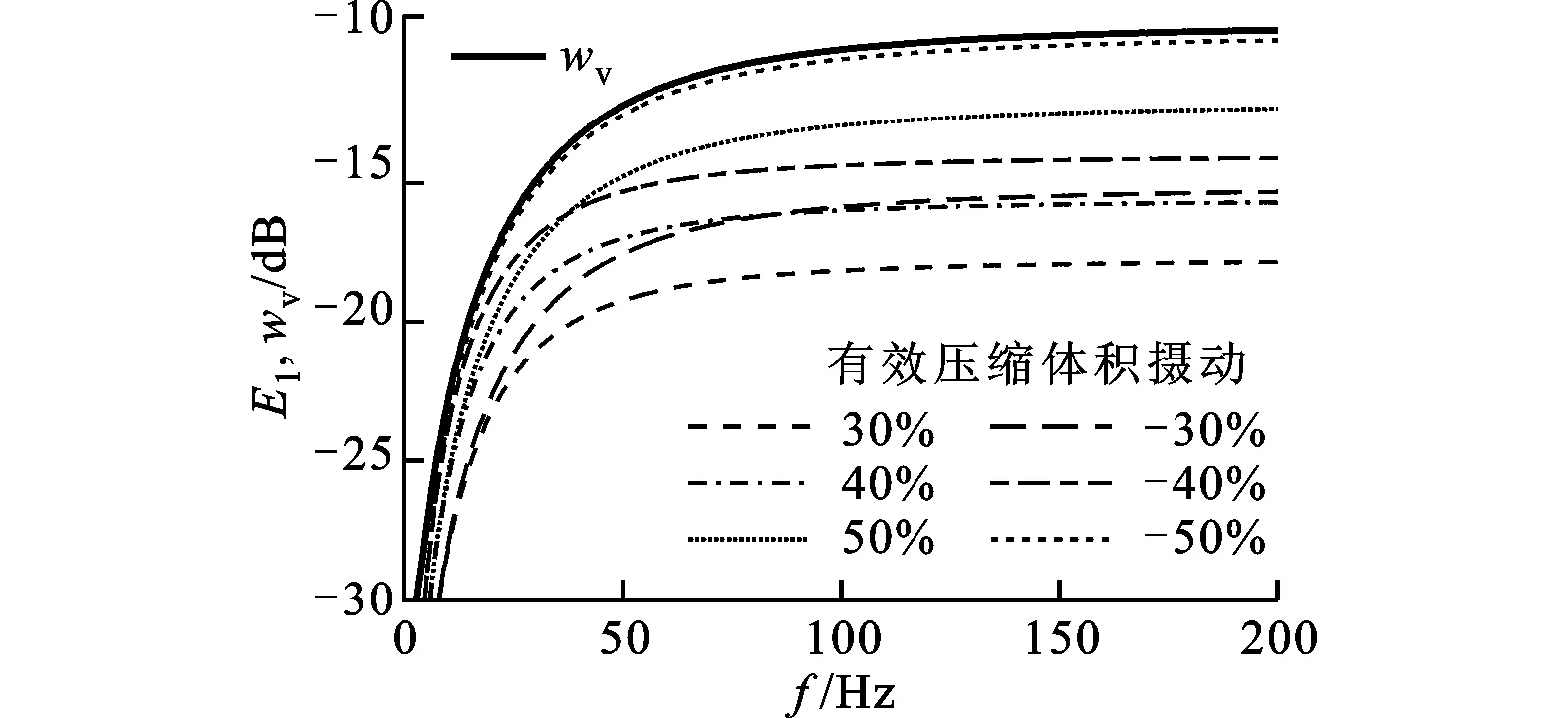
(b)壓縮體積攝動(dòng)下GQPL的相對(duì)誤差E1、權(quán)重函數(shù)wv隨頻率的變化

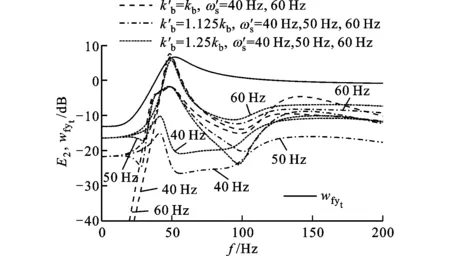
(c)極限情況下Gfyt的相對(duì)誤差E2、權(quán)重函數(shù)wfyt隨頻率的變化

(d)極限情況下Gfyr的相對(duì)誤差E3、權(quán)重函數(shù)wfyr隨頻率的變化

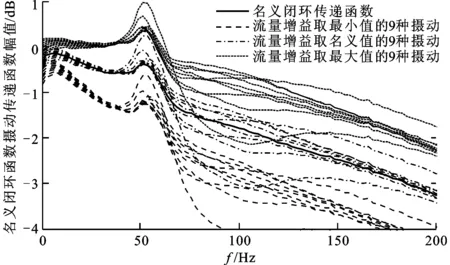
圖10 名義閉環(huán)傳遞函數(shù)和27種攝動(dòng)情況下傳遞函數(shù)的幅頻特性

引入如圖7所示的前饋補(bǔ)償來(lái)進(jìn)一步拓展系統(tǒng)頻寬,文中選取的期望模型為

Gd=1/[(s/400π+1)(s2/(600π)2+1.4s/600π+1)]

(7)

經(jīng)前饋補(bǔ)償后,在控制系統(tǒng)中引入前置濾波器將加速度參考轉(zhuǎn)換為位移參考,此時(shí)振動(dòng)臺(tái)上平臺(tái)加速度at相對(duì)于加速度參考的頻率響應(yīng)如圖11中虛線(xiàn)所示。比較采用和未采用兩自由度控制算法的情況,如圖11中虛線(xiàn)和點(diǎn)劃線(xiàn)所示,可知前饋補(bǔ)償控制已顯著提高了系統(tǒng)的頻寬,具體來(lái)說(shuō)將系統(tǒng)頻寬從21Hz提高到63 Hz。但是,這與伺服控制策略的預(yù)期頻寬仍相距很大,造成此結(jié)果的主要原因在于輕柔基礎(chǔ)在其固有頻率(100Hz)附近對(duì)系統(tǒng)性能的限制。為此,在前置濾波器后端加入幾何解耦控制器消除輕柔基礎(chǔ)與上平臺(tái)間的動(dòng)態(tài)耦合,經(jīng)解耦控制算法后,系統(tǒng)的頻寬提高至250Hz左右,已完全滿(mǎn)足系統(tǒng)的頻寬要求,如圖11中的實(shí)線(xiàn)所示。

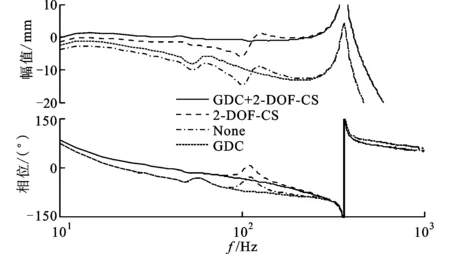
圖11 不同控制算法的比較

最后,通過(guò)仿真驗(yàn)證負(fù)載干擾力補(bǔ)償控制器的作用。將巖土模型動(dòng)態(tài)特性變化分為劇烈下降和隨機(jī)波動(dòng)兩部分。文中采用的位移參考為50Hz的正弦信號(hào),其頻率恰為巖土模型的固有頻率,此時(shí)負(fù)載力對(duì)系統(tǒng)特性的影響最為顯著。當(dāng)負(fù)載動(dòng)態(tài)特性未發(fā)生變化時(shí),位置閉環(huán)的響應(yīng)信號(hào)如圖12中P1段所示,可看出經(jīng)負(fù)載干擾力補(bǔ)償控制后,系統(tǒng)的相位滯后、幅值衰減僅有輕微改善。當(dāng)巖土模型的固有頻率和阻尼比突然下降至初始值的45%左右時(shí),系統(tǒng)對(duì)正弦位移參考的響應(yīng)如圖12中P2段所示,可以看出采用負(fù)載干擾力補(bǔ)償控制器的位置系統(tǒng)能更快地回到穩(wěn)定狀態(tài),且在過(guò)渡過(guò)程的超調(diào)也減少至未采用補(bǔ)償?shù)?0%左右。過(guò)渡完成之后,系統(tǒng)進(jìn)入隨機(jī)波動(dòng)階段。當(dāng)巖土模型固有頻率的變化范圍為初始值的40%～80%、阻尼比變化范圍為初始值的40%～80%時(shí),系統(tǒng)的響應(yīng)信號(hào)如圖12中P3段所示。從P3段可知,采用負(fù)載干擾力補(bǔ)償后系統(tǒng)的波形失真度也顯著改善。綜上所述,干擾力補(bǔ)償控制器可有效抑制負(fù)載動(dòng)態(tài)特性變化對(duì)系統(tǒng)性能的影響。

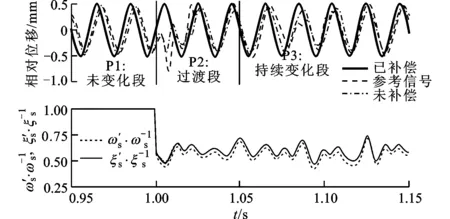
圖12 負(fù)載特性攝動(dòng)時(shí),采用和未采用干擾力補(bǔ)償器的系統(tǒng)對(duì)正弦位移參考的復(fù)現(xiàn)對(duì)比

5 結(jié) 論

本文引入幾何解耦控制器,消除了輕柔基礎(chǔ)與上平臺(tái)間的動(dòng)態(tài)耦合;引入負(fù)載干擾力補(bǔ)償控制器,抑制了負(fù)載動(dòng)態(tài)特性變化對(duì)系統(tǒng)性能的影響;最終,結(jié)合兩自由度控制、魯棒控制策略設(shè)計(jì)了系統(tǒng)的前饋、反饋控制器。仿真結(jié)果表明,該復(fù)合控制策略可有效提高單軸離心振動(dòng)臺(tái)系統(tǒng)在非線(xiàn)性、耦合特性影響下的性能。

[1] 張建民, 于玉貞, 濮家騮, 等. 電液伺服控制離心振動(dòng)臺(tái)系統(tǒng)研制 [J]. 巖土工程學(xué)報(bào), 2004, 26(6): 843-845. ZHANG Jianmin, YU Yuzhen, PU Jialiu, et al. Development of a shaking table in electro-hydraulic servo-control centrifuge [J]. Chinese Journal of Geotechnical Engineering, 2004, 26(6): 843-845.

[2] 王永志. 振動(dòng)離心機(jī)系統(tǒng)工作原理與初步設(shè)計(jì) [D]. 哈爾濱: 中國(guó)地震局工程力學(xué)研究所, 2010.

[3] CONTE J P, TROMBETTI T L. Linear dynamic modeling of a uni-axial servo-hydraulic shaking table system [J]. Earthquake Engineering and Structural Dynamics, 2000, 29: 1375-1404.

[4] 羅中寶, 楊志東, 叢大成, 等. 大型液壓離心振動(dòng)臺(tái)的耦合特性分析 [J]. 振動(dòng)與沖擊, 2014, 33(11): 17-25. LUO Zhongbao, YANG Zhidong, CONG Dacheng, et al. The coupling characteristic analysis of large hydraulic centrifugal shaker [J]. Journal of Vibration and Shock, 2014, 33(11): 17-25.

[5] STOTEN D P, SHIMIZU N. The feedforward minimal control synthesis algorithm and its application to the control of shaking-tables [J]. Proceedings of the IMechE: Part I Journal of Systems and Control Engineering, 2007, 221: 423-444.

[6] GIZATULLIN A O, EDGE K A. Adaptive control for a multi-axis hydraulic test rig [J]. Proceedings of the IMechE: Part I Journal of Systems and Control Engineering, 2006, 221: 183-198.

[7] CUYPER J D, VERHAEGEN M, SWEVERS J. Off-line feed-forward and Hinf feedback control on a vibration rig [J]. Control Engineering Practice, 2003, 11: 129-140.

[8] VAES D, ENGELEN K, ANTHONIS J, et al. Multivariable feedback design to improve tracking performance on tractor vibration test rig [J]. Mechanical Systems and Signal Processing, 2007, 21: 1051-1075.

[9] UCHIYAMA Y, MUKAI M, FUJITA M. Robust control of electrodynamic shaker with 2DOF control using Hinf filter [J]. Journal of Sound and Vibration, 2009, 326: 75-87.

[10]IWASAKI M, ITO K, KAWAFUKU M, et al. Disturbance observer-based practical control of shaking tables with nonlinear specimen [C]∥Proceedings of the 16th IFAC World Congress International Federation of Automatic Control. Piscataway, NJ, USA: IEEE, 2005: 1251-1256.

[11]UCHIYAMA Y, FUJITA M. Robust disturbance-force compensator for time waveform replication of an electrodynamic shaker [J]. JSME Journal of System Design and Dynamics, 2010, 4(1): 1-12.

[12]HE Yunbo, CHUA P S, LIM G H. Performance analysis of a two-stage electrohydraulic servovalve in centrifugal force field [J]. Journal of Fluids Engineering, 2003, 125: 166-170.

(編輯 武紅江)

ACombinedControlStrategyforLargeUniaxialCentrifugalShaker

LUO Zhongbao,YANG Zhidong,CHEN Liang,CONG Dacheng

(School of Mechatronics Engineering, Harbin Institute of Technology, Harbin 150001, China)

A combined control strategy based on traditional servo control strategies is proposed to solve the dynamic coupling between the light-flexible base and the table, and to overcome the performance deterioration of centrifugal shaker caused by nonlinear factors. A geometry decoupling controller based on the equivalent coupling model is designed to eliminate the dynamic coupling between the light-flexible base and the table. Effects of all nonlinear factors on the system performance are taken into account, and a feedback controller based on robust control and a feed-forward controller based on 2-DOF control are presented to ensure the stability and control accuracy of the system. A load disturbing force compensator is also introduced to counteract the influence of load characteristics variation on system performance. Simulation results show that the bandwidth of the centrifugal shaker is improved to 250Hz after the feedback and feed-forward adjusting and geometry decoupling, and satisfies the anticipated bandwidth requirement of servo control strategy. When the load disturbing force is compensated, the overshoot and adjustment time of position close-loop in the radical drop section of load characteristics reduce to 50% of that without using compensation, and the close-loop waveform distortion in the random fluctuation section of load characteristics is also improved.

centrifugal shaker; geometry decoupling controller; robust control; 2-DOF control strategy

2014-03-10。

羅中寶(1986—),男,博士生;叢大成(通信作者),男,教授,博士生導(dǎo)師。

國(guó)家自然科學(xué)基金資助項(xiàng)目(51205077)。

10.7652/xjtuxb201412021

TU352.1

:A

:0253-987X(2014)12-0131-09