鈾礦堆浸分形動力學模型

宋鍵斌，丁德馨，葉勇軍，李廣悅，扶海鷹，胡 南，王永東

(南華大學 鈾礦冶生物技術國防重點學科實驗室，湖南 衡陽 421001)

堆浸是現代工業回收金屬礦物最常用的技術之一[1-2]，它是一將有用元素從礦石轉移到浸出液中的固液轉移過程[3]，有投入低、見效快、操作管理簡單、環境友好等諸多優點[4]，所以在低品位鈾礦的回收利用方面得到了廣泛應用[5]。

可靠的工藝數據參數需從綜合的柱浸試驗程序中按比例獲取，因此，許多學者在堆浸模型和理論方面展開了大量研究。Box等[6]首次提出堆浸的數學模型，該模型主要體現了顆粒大小及孔隙率與浸出率的關系。Dixon等[7-8]在擴散模型的基礎上，考慮了滲流速率、礦堆高度、溶浸液濃度以及顆粒孔隙度、粒徑等因素對浸出的影響，建立了從球形顆粒中浸取多種固體反應物的數學模型。Lizama[9]對堆浸礦石粒度的影響進行了研究，在對各小范圍離散粒徑分布的礦石開展的浸出試驗中，分別取其粒徑平均值和標準差進行了數值模擬。Mellado等[10]基于伯努利方程建立了堆浸的多個解析模型，用于識別不同規模浸堆的浸出時間特征。

目前國內外眾多堆浸模型在研究礦石顆粒大小對浸出的影響時，大多采用礦石平均粒徑代替全礦粒徑，或只考慮小范圍離散型粒徑分布礦石的浸出效果，這與生產實際相差甚遠。事實上，礦石經破碎機破碎后，粒徑分布更廣泛，且具有其特定的粒徑分布特征，分布規律取決于破碎機的參數和礦石的性質。自Mandelbrot創立分形幾何學以來，分形理論已被廣泛運用于各個領域，礦物冶金方向也有所涉及。Fazeli等[11]認為可用粒徑分維數來描述具有特定粒徑分布特征的礦石，曾晟等[12]研究了礦巖破碎塊度分形分布對鈾浸出的影響，這些研究表明形狀與大小各異的巖體顆粒具有其特定的分形特性，且不同的分維數和有用元素的浸出有著密切的聯系。

本試驗將基于Mellado等于2009年建立的堆浸解析模型，對具有不同粒徑分布特征的鈾礦石散體開展室內柱浸試驗研究，分析鈾礦石浸出率變化規律與分維數的關系，并建立不同粒徑分維數鈾礦石的浸出動力學方程。

1 動力學分析

Mellado等研究了礦石堆浸的規律，建立了如下動力學方程：

(1)

(2)

Mellado等提出，當堆浸過程中溶劑的DAe、ε0、εh等不變時，不同粒徑礦石的浸出率與時間的函數關系式為：

(3)

他們用該方程對Dixon等的實驗數據進行了擬合，取得了良好的擬合結果。值得注意的是，在擬合過程中Mellado等用平均粒徑代替了全礦粒徑，顯然這和實際不相符，一個生產礦堆的礦石具有其特定的粒徑分布特征，不能簡單地用平均粒徑代替。

Fazeli等認為可用粒徑分維數來描述具有特定粒徑分布特征的礦石，其假設在某一三維空間內，不小于某一粒徑R的顆粒構成的全體體積V為：

V(r>R)=Cv[1-(R/λv)3-D]

(4)

式中：Cv和λv分別為描述巖塊體積形狀和尺寸的常數；V(r>R)為顆粒尺寸不小于R的顆粒體積；D為粒徑分布分維數，D∈(0，3)。

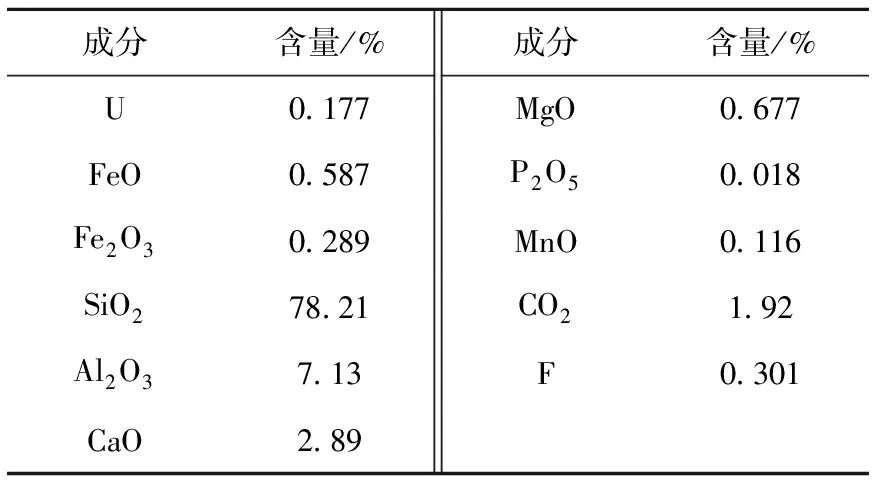
若不同顆粒大小的礦石密度ρ相同，將式(4)變形，得到小于粒徑R的礦石的質量M(r

(5)

式中：MT為所有礦石的總質量；RL為礦石的最大粒徑。

這里，將質量為M(r

πNρR3

(6)

(7)

對式(7)繼續簡化，得粒徑R和分維數D的函數關系為：

(8)

(9)

將式(8)、(9)代入式(2)得：

(10)

其中：q=3(1-εh)DAe；kτ′=kτDAe/ε0。

而Mellado等[14-15]又認為由于堆浸過程中，礦堆不同深度存在不同程度的溝流、沉淀、結塊等現象，極大地影響了內擴散和外擴散，使得有用元素不可能完全浸出，那么y∞→1不成立，則提出y∞隨礦堆深度的變化關系如式(11)所示，并已證實其符合事實規律。

(11)

同樣地，我們認為不同分維數的鈾礦石也存在著上述現象，y∞也將因分維數的變化而變化，這里先假設y∞隨分維數的變化關系如式(12)所示：

y∞=y∞(D)

(12)

α=α(D)

(13)

那么，在不考慮堆浸過程中DAe、ε0、εh等變化時，不同粒徑分維數礦石的浸出動力學方程即為式(14)：

y(t)=R∞(D)(1-(1-α(D))·

(14)

2 試驗

2.1 試驗材料

試驗用鈾礦石取自我國南方某鈾礦山，破碎后粒徑分布在0～9 mm之間，經標準的實驗分析，其主要化學成分列于表1。由表1可知，礦石化學成分復雜，脈石礦物主要是硅酸鹽類礦物，由于該鈾礦企業工業生產中采用酸法浸礦，所以本文也采用酸法浸出開展試驗研究。

表1 試驗鈾礦石的主要化學成分

2.2 試驗方法

用標準篩將鈾礦石原礦篩分成10個不同粒級范圍(0/-0.5、+0.5/-1、+1/-2、+2/-3、+3/-4、+4/-5、+5/-6、+6/-7、+7/-8、+8/-9 mm)，設定每組分維數鈾礦石樣重為10 kg，根據式(5)對各粒級鈾礦石稱取相應的質量，分別配制成5組分維數為1.6、1.8、2.0、2.2、2.4的試驗礦樣。例如分維數為2.4的礦樣，各粒級鈾礦石稱取量分別為1.77、0.91、1.38、1.12、0.97、0.88、0.81、0.76、0.72、0.68 kg，然后充分混合均勻。5組礦樣相對應的各級鈾礦石含量累積百分比如圖1所示，根據試驗分析，相應的品位分別為0.172%、0.173%、0.175%、0.179%、0.180%。

試驗柱示意圖如圖2所示。柱長106 cm、內徑88 mm，材質為耐酸有機玻璃。裝礦前、后，為了消除端部效應，在試驗柱的底部和頂部分別鋪設3 cm厚、粒徑1～2 mm的石英砂。裝礦過程中，將試驗柱傾斜，緩慢倒入鈾礦石，盡量減弱鈾礦石因從高處倒入而產生的偏析現象。頂部石英砂鋪設完后，在其表面正中央放1塊扁平鵝卵石，然后蓋上密封蓋。

圖1 不同粒徑分布分維數鈾礦級配圖

圖2 試驗柱示意圖

布液前用適量清水將每根試驗柱的鈾礦石潤濕，隨后按液固比為0.1 L/kg的比例，每天配置1 L一定濃度的稀硫酸溶液，并連續布液8 h，硫酸濃度根據試驗柱浸出液pH值的變化做相應調整，確保后期浸出液pH值在1～2之間。布液記錄如表2所列，稀硫酸濃度平均值為16.4 g/L。持續的監測隨即展開，在第2天布液前，分別從各集液池取樣，監測樣品的pH值、電位、鈾濃度等。

2.3 試驗結果與討論

5組具有不同粒徑分維數特征的鈾礦石對應的鈾累積浸出率隨布液時間的變化趨勢如圖3所示。由圖3可知，浸出初期浸出率緩慢上升，且分維數越大浸出率上升越慢，持續時間也越長；浸出中期浸出率先迅速增大而后放緩，分維數不同浸出速率和持續時間皆不同；而中、后期速率穩定且分維數高的試驗柱的浸出率逐漸超過分維數低的試驗柱的浸出率。

表2 布液記錄

圖3 不同粒徑分布分維數礦樣鈾累積浸出率隨布液時間的變化

觀察布液終點鈾累積浸出率的值隨分維數的變化趨勢，并結合y∞∈(0，1)，假設y∞隨分維數的變化如式(15)所示，且同時假設α隨分維數的變化關系如式(16)所示：

(15)

(16)

當然，y∞和α與分維數的關系式有很多種選擇，對于不同分維數的鈾礦石，不論浸出條件如何，y∞和α均須滿足y∞∈(0，1)、α∈(0，1)，依據此條件方能判定式(15)、(16)是否能正確表示鈾浸出規律和不同分維數的關系。

將式(15)、(16)代入式(14)得：

(17)

用Matlab6.5將圖3中的實測值對式(17)進行擬合。擬合前首先將已知條件代入式(17)中：由稀硫酸平均濃度16.4 g/L換算得硫酸體積分數為0.009 1，即εb=0.009 1；擬合時以天為基本時間單位，則由布液量除以截面積再除以時間得到布液強度us=49.35 cm3/(cm2·d)；試驗柱裝礦高度z=100 cm；鈾礦石最大顆粒半徑R=0.45 cm。然后設定擬合的邊界條件：p∈(1，∞)，q∈(0，∞)，m∈(0，∞)，n∈(0，∞)，kθ∈(0，∞)，kτ′∈(0，∞)。需指出的是，5組數據需同時擬合，這樣獲得的方程方能用作其他分維數情況下的插值計算或驗證，本文利用Matlab6.5的面擬合工具。

擬合結果如圖4所示，參數p=5.766，q=448.5，m=3.102，n=1.102，kθ=0.001 376，kτ′=0.144，擬合相關系數為0.977 8。

圖4 不同分維數鈾礦石鈾累積浸出率隨布液時間變化的面擬合圖

將擬合結果代入式(15)、(16)，當分維數取不同值時，y∞和α相應的計算值分別為：y∞(D=1.6)=0.813 9、y∞(D=1.8)=0.834 6、y∞(D=2.0)=0.851 1、y∞(D=2.2)=0.864 7、y∞(D=2.4)=0.876；α(D=1.6)=0.493 9、α(D=1.8)=0.550 2、α(D=2.0)=0.595 1、α(D=2.2)=0.631 9、α(D=2.4)=0.662 6，這些均符合y∞∈(0，1)、α∈(0，1)的要求，說明式(15)、(16)能正確表達y∞和α關于分維數的關系。

2.4 試驗驗證

為驗證式(17)作為不同粒徑分維數鈾礦石的浸出動力學方程是否合理，另稱取1組總重約10 kg的原礦，該組鈾礦石相應的各粒級鈾礦石含量累積百分比如圖5所示，將圖5中的數據轉換后按式(5)擬合得到原礦的分維數為1.902。

圖5 鈾礦石原礦級配圖

與其他試驗柱相同，裝鈾礦石前、后，在試驗柱的底部和頂部分別鋪設3 cm厚、粒徑1～2 mm的石英砂，用適量清水潤濕后，按液固比為0.1 L/kg的比例，每天配置1 L一定濃度的稀硫酸溶液，并連續布液8 h，硫酸濃度根據試驗柱浸出液pH值的變化做相應調整，確保后期浸出液pH值在1～2之間，柱浸35 d后，獲得1組浸出率實測數據。同時將2.3節中擬合出的參數代入式(6)，令D=1.902，獲得1組分維數為1.902的鈾礦石浸出率的預測值，將預測值和實測值相比較，結果如圖6所示，兩者標準差按下式計算：

圖6 鈾礦石原礦累積浸出率實測值與預測值的比較

(18)

計算得到d=0.057 1，這表明擬合值與實測值的平均相對偏差為5.71%，相對偏差較小，其主要是由試驗誤差及擬合中各參數的變化引起的。很顯然，擬合結果能很好地反映不同分維數鈾礦石浸出率隨時間的變化規律，也即表明式(17)可作為不同粒徑分維數鈾礦石的浸出動力學方程。

3 結論

1) 本文基于分形理論，用堆浸鈾礦石的粒徑分布分維數代替其平均粒徑，對Mellado等提出的礦石堆浸動力學模型進行了改進，進一步通過柱浸試驗，采用擬合法確定了鈾礦堆浸分形動力學模型參數y∞和α與分維數的關系，從而建立并驗證了如下鈾礦堆浸分形動力學模型：

2) 依據試驗結果，該鈾礦堆浸分形動力學模型不論是對不同分維數鈾礦石浸出規律的擬合，還是對其他任意分維數鈾礦石浸出規律的預測，都有較好的精度。

3) 由于破碎設備、工藝等不同，實際生產中的鈾礦石具有不同的分維數，其堆浸效果也不盡相同，建立鈾礦堆浸分形動力學模型，研究不同分維數鈾礦石的浸出規律，對指導調控破碎條件、提高鈾浸出率有一定的現實意義。

參考文獻：

[1] MOUSAVI S M, YAGHMAEI S, VOSSOUGHI M, et al. Comparison of bioleaching ability of two native mesophilic and thermophilic bacteria on copper recovery from chalcopyrite concentrate in an airlift bioreactor[J]. Hydrometallurgy, 2005, 80(1-2): 139-144.

[2] GHORBANI Y, BECKER M, MAINZA A, et al. Large particle effects in chemical/biochemical heap leach processes: A review[J]. Minerals Engineering, 2011, 24(11): 1 172-1 184.

[3] CARIAGA E, CONCHA F, SEPULVEDA M. Flow through porous media with applications to heap leaching of copper ores[J]. Chemical Engineering Journal, 2005, 111(2-3): 151-165.

[4] WATLING H R. The bioleaching of sulphide minerals with emphasis on copper sulphides: A review[J]. Hydrometallurgy, 2006, 84(1-2): 81-108.

[5] BENNETT C R, MCBRIDE D, CROSS M, et al. A comprehensive model for copper sulphide heap leaching, Part 1: Basic formulation and validation through column test simulation[J]. Hydrometallurgy, 2012, 127-128: 150-161.

[6] BOX J C, PROSSER A P. A general model for the reaction of several minerals and several reagents in heap and dump leaching[J]. Hydrometallurgy, 1986, 16(1): 77-92.

[7] DIXON D G, HENDRIX J L. A mathematical model for heap leaching of one or more solid reactants from porous ore pellets[J]. Metallurgical Transactions, 1993, 24(6): 1 087-1 102.

[8] DIXON D G, HENDRIX J L. A general model for leaching of one or more solid reactants from porous ore particles[J]. Metallurgical Transactions, 1993, 24(1): 157-169.

[9] LIZAMA H M. A kinetic description of percolation bioleaching[J]. Minerals Engineering, 2004, 17(1): 23-32.

[10] MELLADO M E, CISTERNAS L A, GALVEZ E D. An analytical model approach to heap leaching[J]. Hydrometallurgy, 2009, 95(1-2): 33-38.

[11] FAZELI M, SHORAFA M, NAMDAR-KHOJASTEH D, et al. A fractal approach for estimating soil water retention curve[J]. Journal of Soil Science and Environmental Management, 2010, 1(7): 177-183.

[12] 曾晟，譚凱旋. 礦巖破碎塊度分布分形特征對鈾浸出率的影響[J]. 礦冶工程，2011，31(1)：16-18.

ZENG Sheng, TAN Kaixuan. Effect of fractal feature of the crushing size distribution on uranium leaching rate[J]. Mining and Metallurgical Engineering, 2011, 31(1): 16-18(in Chinese).

[13] MELLADO M E, CISTERNAS L A. An analytical-numerical method for solving a heap leaching problem of one or more solid reactants from porous pellets[J]. Computers and Chemical Engineering, 2008, 32(10): 2 395-2 402.

[14] MELLADO M E, CASANOVA M P, CISTERNAS L A, et al. On scalable analytical models for heap leaching[J]. Computers and Chemical Engineering, 2011, 35(2): 220-225.

[15] MELLADO M E, GALVEZ E D, CISTERNAS L A. On the optimization of flow rates on copper heap leaching operations[J]. International Journal of Mineral Processing, 2011, 101(1-4): 75-80.