超臨界水通道內壓降特性分析

徐 莉，臧金光,2，曾小康，閆 曉

(1.中國核動力研究設計院 中核核反應堆熱工水力技術重點實驗室，四川 成都 610041；

2.清華大學 工程物理系，北京 100084)

在反應堆中，堆芯釋放的熱量由系統回路中的冷卻劑帶出，堆芯的輸熱能力與冷卻劑的流動特性密切相關，堆芯內冷卻劑的流量分配對堆芯冷卻劑溫度場、燃料元件表面溫度分布均有重要影響。在熱工水力設計的過程中，應盡量使冷卻劑的流量分布與堆芯功率分布相匹配，以最大限度地提高反應堆的運行功率，同時保證反應堆的安全性。分析冷卻劑的壓降特性是堆芯熱工水力設計的重要方面[1]。

超臨界水冷堆是利用超臨界狀態下的水作為冷卻劑和慢化劑的第4代核能系統[2]。超臨界條件下由于存在劇烈的物性變化，壓降特性具有自身的特點。超臨界水在擬臨界點前后密度有較大落差，重力壓降需考慮密度的沿程積分效應，同時密度的明顯變化使得加速壓降相比亞臨界條件下更為明顯。在等溫條件下，摩擦系數均為雷諾數的單值函數；而在加熱條件下，近壁面邊界層處的流體物性與主流體物性的差別較大，摩擦系數的計算需考慮近壁面處的物性修正。超臨界條件下的摩擦關系式多以亞臨界條件下的關系式為基礎加以擴展。

本文對超臨界條件下的流動特性進行研究。

1 壓降類型

一般而言，通道內的流動壓降可分為加速壓降、重力壓降、摩擦壓降和局部壓降，本文著重分析加速壓降、重力壓降和摩擦壓降在超臨界條件下的變化規律。

在超臨界條件下，擬臨界區附近的密度變化較為劇烈，計算重力壓降時不能簡單認為密度為常數，需考慮密度的沿程積分效應。

(1)

其中：ρ為流體密度；g為重力加速度；Δpg為重力壓降；θ為流道與豎直方向的傾角；L為流動距離；x為積分變量。

采用目前成熟的數值積分方法[3]對式(1)求解，如應用較廣泛的Newton-Cotes求積公式：

(2)

其中：xi為求積節點；n為積分階數；Ai為求積系數，定義式如下：

(3)

其中：li(x)為拉格朗日插值基函數；a、b為積分上、下限。

當n=1時，式(2)為梯形求積公式：

h=b-a

(4)

當n=2時，式(2)為辛普森求積公式：

h=(b-a)/2

(5)

當n=3時，式(2)為牛頓求積公式：

3f(x2)+f(x3))h=(b-a)/3

(6)

其中，xi=a+ih。

以辛普森求積公式計算重力壓降為例：

(7)

除以上數值積分方法外，也有研究者建議采用其他方法，如Ornatskiy等推薦采用焓值平均來考慮密度的積分效應[4]：

(8)

為衡量這些積分表達式間的區別，分別用以上方法計算了壓力為25 MPa下不同焓值區間的平均密度，其中精確值采用精確分段法，將焓值的積分區間劃分50個節點，再線性平均后得到。圖1示出不同焓值區間下的平均密度，其中工況編號1～5分別代表焓值區間為1 850～2 000、1 850～2 200、1 850～2 400、1 850～2 600和2 300～3 000 kJ/kg。由圖1可見：當焓值區間較小時，密度變化較小，采用不同方法計算的結果相差不大；當焓值區間逐漸擴大時，梯形求積法差異最大，最大相對誤差達11%，而辛普森求積法的最大相對誤差為0.9%，牛頓求積法的最大相對誤差為0.6%，Ornatskiy法的最大相對誤差為1.2%[4]。大部分情況下，采用Ornatskiy法計算密度的平均值是合理的，也易于實現。辛普森求積法在計算精度上較Ornatskiy法好些，但需多調用一次物性函數。

圖1 不同焓值區間的積分方法比較

亞臨界條件下，計算單相流的摩擦壓降Δpf普遍采用Darcy公式[1]：

(9)

其中：f為Darcy-Weisbach摩擦系數；Δz為單位通道長度；De為通道水力直徑；v為流體平均速度；G為質量流速。

加速壓降Δpa的計算公式為：

(10)

式中：ρout、ρin分別為通道出口和入口的流體密度；Vout、Vin分別為相應位置的比體積。

圖2 不同壓降梯度的沿程變化

圖2示出用CFX計算的光滑2×2棒束結構各項壓降梯度的對比。由圖2可見，加速壓降梯度與摩擦壓降梯度沿程一直增大，而重力壓降梯度沿程一直減小。由3項壓降梯度的定義式可知，重力壓降梯度與平均密度呈正比，摩擦壓降梯度與流體密度呈反比，加速壓降梯度與流體比體積的落差呈正比。在整個加熱過程中，單位通道長度上的流體密度隨溫度的升高而下降，比體積上升，導致加速壓降梯度和摩擦壓降梯度增大和重力壓降梯度減小。在通道入口區，重力壓降梯度最大，其次是摩擦壓降梯度；之后，摩擦壓降梯度逐漸增大，而重力壓降梯度逐漸減小，使得前者慢慢超過后者。

圖3示出絕熱條件(冷態)和加熱條件(熱態)下各項壓降梯度的對比。絕熱條件下，加速壓降梯度為零。由圖3可見：摩擦壓降梯度和重力壓降梯度一直維持不變；加熱后，由于沿程物性的變化，加速壓降梯度產生，且沿程逐步增大；重力壓降梯度相比絕熱條件時減少，沿程伴隨密度的下降而下降；摩擦壓降梯度比絕熱條件時略有增加。加熱后總壓降梯度比絕熱條件時的略有上升。實際堆芯設計中，由于堆芯內結構復雜，棒束通道和通道阻塞物很多，加上在超臨界條件下冷卻劑溫度要跨過擬臨界區，因此可能會使堆芯內的壓降變化很大。這是進行超臨界條件流動實驗時必須要考慮的問題。

圖3 冷態與熱態時不同壓降梯度的沿程變化

2 亞臨界單相摩擦關系式

超臨界條件下的摩擦關系式多以亞臨界單相摩擦關系式為基準，再輔以壁面物性與主流體物性之比作為修正，其優點在于當壁面溫度與主流體溫度之差較小時，摩擦關系式能自然過渡到正常等溫條件。因此，發展超臨界條件下的摩擦關系式需選取一合適的亞臨界等溫摩擦關系式為基礎。

亞臨界條件的等溫摩擦關系式中適用范圍較廣及預測精度較高的關系式之一是經典的隱式PKN公式(式(11))，它是由Prandtl等根據大量實驗測量結果得到的一半理論、半經驗關系式[5]，與大量實驗數據具有較好的一致性。

(11)

隱式PKN公式計算較為復雜，需不斷迭代，用于發展超臨界條件下摩擦公式時會有些不便。基于隱式PKN公式形式，通過簡單數學推導，可得到PKN公式的顯式形式。顯式PKN公式在精度與適用范圍上與隱式PKN公式相當，同時免去了復雜的迭代過程。顯式PKN公式是將Blausius公式代入隱式PKN公式，經化簡整理，得：

f=1/(1.75lgRe-1.3)2

(12)

為便于分析比較，選取其他幾個常用公式作為比較。

McAdams公式：

f=0.184Re-0.2

(13)

Blausius公式：

f=0.316 4Re-0.25

(14)

Filonenko公式：

f=1/(1.82lgRe-1.64)2

(15)

為驗證推導的顯式PKN公式與隱式PKN公式的接近程度，同時比較各摩擦系數公式的預測性能，分別計算了它們在不同雷諾數范圍內的摩擦系數，結果示于圖4。由圖4可見：當雷諾數較小時，McAdams公式的計算結果明顯小于隱式PKN公式的，隨著Re減小，誤差增大；當

Re較高時，McAdams公式的計算結果逐漸與隱式PKN公式的接近，可見McAdams公式主要適用于高Re范圍；在所考察的Re范圍內，Blausius與Filonenko公式的計算結果均與隱式PKN公式的接近，只是在Re較小時，Filonenko公式的計算結果略大于隱式PKN公式的，Blausius公式的計算結果則略小；而本文推導的顯式PKN公式的計算結果在整個Re范圍內均與隱式PKN公式的最接近。這可從推導的過程中看出，顯式PKN公式是將Blausius公式作為初值代入隱式PKN公式獲得的，Blausius公式本身具有相對較好的預測性能，經過隱式PKN公式的迭代修正后，會更接近于隱式PKN公式，這是它比其他公式預測性能更好的原因。圖5示出各摩擦關系式計算結果的區別。

3 超臨界摩擦關系式

針對超臨界條件下流動實驗的研究目前還不充分，缺少較普遍認可的摩擦關系式，對其中的機理仍有待于進一步研究。

以下是一些研究者基于實驗數據擬合出的超臨界條件下的摩擦關系式[4]。

Mikheev公式：

f=fiso(Prw/Prb)1/3

(16)

其中：fiso為等溫流動摩擦系數；Prw、Prb分別為以壁面溫度和主流體溫度為特征溫度得到的流體普朗特數。

Popov公式：

/ρb)0.74

(17)

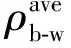
圖4 各摩擦關系式計算結果比較

圖5 各摩擦關系式計算結果的差異

Kondrat’ev公式：

f=0.188Re-0.22

(18)

Kirillov公式：

f=fiso(μw/μb)0.4

(19)

其中，μw和μb分別為壁面和主流體的動力黏度。

上述公式中的fiso均采用Filonenko公式計算。鑒于實驗數據不充分，本文利用CFD方法比較了這幾組基于實驗的摩擦關系式與數值結果的差異。選取Mokry等[6]開展的超臨界條件下豎直圓管的傳熱實驗為參考，管長為4 m，

直徑為10 mm，質量流速G為203～1 495 kg/(m2·s)，熱流密度q為335～884 kW/m2，實驗工況列于表1。

表1 實驗工況

以Fluent軟件為計算平臺，ICEM為幾何建模和網格劃分工具，生成二維四面體結構化網格。合理控制邊界層的網格參數，使第1層網格的y+<1，同時開展網格的無關性分析，確保計算結果不依賴于網格參數。入口采用定速度邊界條件，給定入口溫度；出口設置相對靜壓值為零，組件盒采用無滑移絕熱壁面邊界條件；元件棒表面依據計算工況不同設置定熱流密度邊界條件。計算時選用SST湍流模型。

圖6示出不同摩擦關系式與Fluent數值結果沿程預測性能的比較。由圖6可見，各摩擦關系式呈現較大的分散性。仔細分析這些關系式的變化趨勢可發現：大部分超臨界條件加熱工況下的摩擦系數均小于亞臨界條件等溫工況下的摩擦系數，Filonenko關系式是亞臨界下的摩擦關系式，整體預測數值最高；超臨界加熱工況下，壁面溫度會遠高于主流體溫度，近壁面處流體的黏性和密度均小于主流體的黏性和密度，導致摩擦系數變小。這與大部分摩擦關系式的修正方向是一致的。

圖6 Fluent與各關系式計算結果的比較

在擬臨界點附近，動力黏度迅速下降，通道流體平均雷諾數上升，摩擦系數下降；同時，當壁面溫度超過擬臨界點、而主流體溫度仍低于擬臨界點時，近壁面處的物性效應明顯，加速了摩擦系數下降的趨勢。這是一些關系式計算的摩擦系數在擬臨界點處迅速下降的原因。在擬臨界點之后，流體溫度遠離擬臨界點區域，壁面流體物性與主流體物性相差較小，物性效應減弱，此時摩擦系數回升。擬臨界點處摩擦系數的極小值現象是超臨界條件下的獨有規律[7]。

在所比較的幾組超臨界摩擦關系式中，Kirillov公式與Fluent的計算結果較為一致，在分析的4組工況中，隨著質量流速和熱流密度的變化，二者的吻合程度均較好，包括擬臨界點處的摩擦系數谷值，只是在入口區Kirillov公式的計算結果略低于Fluent的計算結果，這可能與CFD數值工具在模擬時考慮了入口效應有關。圖7示出Kirillov公式與Fluent計算結果的比較，二者的相對偏差在±10%以內。

圖7 Fluent與Kirillov公式計算結果比較

4 結論

本文分析了超臨界條件下劇烈的物性變化對通道內壓降特性的影響，得到以下結論。

超臨界條件下，擬臨界區前后的密度變化劇烈，使得通道內的加速壓降不可忽略，重力壓降需考慮密度的沿程積分效應。本文比較了不同方法的計算精度，發現梯形求積公式誤差較大，Ornatskiy公式采用焓值平均可有效改善精度，辛普森求積公式與牛頓求積公式的精度較好。

基于隱式PKN公式形式和Blausisu公式得到了顯式PKN公式，計算精度與隱式PKN公式接近，而在具體求解時又免去隱式PKN公式迭代求解的繁瑣，適用于工程上的計算分析。

借助于Fluent的數值分析結果，比較了超臨界條件下不同摩擦關系式的異同，發現物性效應修正會使擬臨界點附近出現局部極值點，且Kirillov公式與Fluent的計算結果較為一致，相對偏差在±10%以內。

參考文獻：

[1] 于平安，朱瑞安，喻真烷，等. 核反應堆熱工水力學[M]. 上海：上海交通大學出版社，2002.

[2] OKA Y, KOSHIZUKA S, ISHIWATARI Y, et al. Super light water reactors and super fast reactors[M]. New York: Springer, 2010.

[3] 鄧建中，劉之行. 計算方法[M]. 西安：西安交通大學出版社，2007.

[4] PIORO I L, DUFFEY R B. Heat transfer and hydraulic resistance at supercritical pressures in power-engineering applications[M]. New York: ASME Press, 2007.

[5] KAKA? S, SHAH R K, AUNG W. Handbook of single-phase convective heat transfer[M]. New York: Wiley-Interscience, 1987.

[6] MOKRY S, PIORO I L, KIRILLOV P, et al. Supercritical-water heat transfer in a vertical bare tube[J]. Nuclear Engineering and Design, 2010, 240: 568-576.

[7] LEI X L, LI H X, YU S Q, et al. Study on the minimum drag coefficient phenomenon of supercritical pressure water in the pseudocritical region[C]∥ICONE20-POWER2012. California, USA: [s. n.], 2012.