單進口輪流放行方式的四路環形交叉口交通信號控制

徐洪峰，耿現彩，何 龍

（大連理工大學 交通運輸學院，遼寧 大連 116024）

0 引 言

環形交叉是道路平面交叉的常見形式。作為城市道路網絡的重要節點，環形交叉口可以采用兩種交通控制方法:讓行規則控制和交通信號控制。按照國際慣例，機動車行經讓行規則控制環形交叉口時，應遵循“入環車輛讓環內車輛先行、環內車輛讓出環車輛先行”的規則通行。實踐證明，在較低或中等機動車交通負荷水平下，與普通平面交叉口相比，讓行規則控制環形交叉口更加安全、高效［1－3］。然而，隨著機動車交通負荷水平的提高，環道車流趨于密集，車輛進出環道的難度加大，違反讓行規則的現象越來越頻繁，由此導致交通事故頻發、通行效率降低、行人和非機動車過街難等交通問題。機動車交通高峰時段，將環形交叉口的交通控制等級由讓行規則控制提升至交通信號控制成為一種必然的選擇。

就環形交叉口的交通信號控制模式而言，根據交通信號燈設置方式的不同分為:①個別進口道控制；②進口道和環道全控制；根據信號配時方案生成方式的不同分為:①預設時間控制；②交通響應控制。目前，國外學者的研究多聚集于“個別進口道控制＋交通響應控制”［4－6］；國內學者的研究多聚集于“進口道和環道全控制＋預設時間控制”［7－10］。

進口道和環道全控制的四路環形交叉口可以采用2種交通組織方式:①多進口同步放行；②單進口輪流放行。多進口同步放行方式下，本向與對向的入環車輛同步獲得通行權，進入環道后，直行車輛可以順利出環，左轉車輛由于受到環道信號燈的阻滯，必須在環道停止線后等待第二次通行機會方能出環。一旦環道停止線后的排隊車輛過多，將嚴重干擾出環車輛的正常通行，導致局部環道乃至整個交叉口陷入死鎖狀態，進而引發區域性的全面交通擁堵。因此，多進口同步放行方式僅適用于環道排隊空間較大或左轉車輛較少的環形交叉口。單進口輪流放行方式下，按照順時針的順序依次為各個進口方向的入環車輛賦予通行權，進入環道后，左轉車輛不會由于受到環道信號燈的阻滯而對直行車輛的正常通行造成干擾，基本消除了局部環道死鎖的可能性。因此，單進口輪流放行方式具有普遍的適用性。此外，與多進口同步放行方式相比，單進口輪流放行方式的環形交叉口在信號配時設計時只需獲取各個進口方向、各條進口道的機動車到達交通量，無需進一步區分機動車的通行方向比例，大大降低了機動車到達交通量調查工作的復雜程度，進一步增強了單進口輪流放行方式的適用性。

就通行空間資源和通行時間資源的結構性特征而言，環形交叉口明顯區別于普通平面交叉口，這意味著傳統的交通信號控制方法無法直接應用于環形交叉口。本文面向機動車交通高峰時段采用“進口道和環道全控制＋預設時間控制”的四路環形交叉口，從相位結構設計和信號配時設計兩個層面，提出一種適用于單進口輪流放行方式的交通信號控制方法，期望為環形交叉口的交通管理與控制工程實踐提供理論依據和技術支持。

1 研究環境與符號解釋

本文的研究環境包括:①在環形交叉口的適當位置安裝有機動車信號燈和行人信號燈；②機動車交通低峰和平峰時段，關閉交通信號燈，環形交叉口采用讓行規則控制；機動車交通高峰時段，開啟交通信號燈，環形交叉口采用交通信號控制；③對于右轉車輛不實施交通信號控制，但它們須主動避讓行人、非機動車和出環車輛；④行人和非機動車實施一體化過街處理；⑤調頭車輛須進入環道完成調頭；⑥機動車相位的信號燈色依次為“綠燈→黃燈→紅燈→綠燈”，行人相位的信號燈色依次為“綠燈→紅燈→綠燈”；⑦采用RiLSA［11］推薦的方法計算綠燈間隔時間。

下文中涉及的符號包括:ad（Ri，Kj）表示相位Kj的排隊頭車進入環道后，在相位Ri的停止線后的允許阻滯時間（s）；BGZ表示相位Z的綠燈啟亮時刻（s）；C表示信號周期時間（s）；Co表示最佳信號周期時間（s）；C（t）o表示最佳信號周期時間的第t輪試算值（s）；Cmax表示最大信號周期時間（s）；Cmin表示最小信號周期時間（s）；dbg（Ri，Kj）表示相位Ri與Kj的綠燈啟亮時間差或相位Kj的綠燈早啟時間（s）；EGZ表示相位Z的綠燈結束時刻（s）；Fi表示行人相位的編號；GZ表示相位Z 的綠燈顯示時間（s）；G（t）Ki表示相位Ki的綠燈顯示時間的第t輪試算值（s）；GminKi，P表示相位Ki保證行人和非機動車安全過街的最小綠燈顯示時間（s）；GminKi，QC表示相位Ki保證一定數量的入環車輛順利通過進口道停止線的最小綠燈顯示時間（s）；GminKi，S表示相位Ki保證行車安全的最小綠燈顯示時間（s）；GminZ表示相位Z 的最小綠燈顯示時間（s）；i＝1，2，3，4；j＝1，2，3，4。i和j同時出現時，（i，j）＝ （1，2），（2，3），（3，4），（4，1）；intg（Z，Z′）表示相位Z與Z′的綠燈間隔時間（s）；Ki表示進口道機動車相位的編號；l（Ri，Kj）表示相位Ri與Kj的停止線間距（m）；QKi，d表示相位 Ki的設計流率（pcu／（h·ln））；Ri表示環道機動車相位的編號；SKi表示相位Ki的飽和流率（pcu／（h·ln））；t為正整數；v（Ri，Kj）表示綠燈啟亮后，相位Kj的入環車輛的進入速度（m／s）；XKi，d表示相位Ki的設計飽和度；X（t）Ki表示相位Ki在最佳信號周期時間的第t輪試算時的理論飽和度，X（t）Ki＝Z、Z′表示任意相位的編號。

2 相位結構設計

相位結構設計的目的是基于平面交叉口的道路空間條件，根據道路使用者的通行需求特征和交通信號控制設備的相關技術條件，遵循一定的原則和步驟，為不同類型、不同行走方向的道路使用者賦予通行權，提供平等的通行機會，定義通行權的傳承順序，實現通行時間資源的戰略分配。

2.1 相位設置

在環道數超過2條的四路環形交叉口內部，存在著大量潛在的交通沖突。隨著進口道機動車信號燈、環道機動車信號燈、行人信號燈的啟用，除了與右轉車輛相關的交通沖突仍需利用讓行規則加以分離外，其他的交通沖突均可以利用交通信號燈進行分離。

單進口輪流放行方式的四路環形交叉口具有4個進口道機動車相位（K1～K4）、4個環道機動車相位（R1～R4）、4個行人相位（F1～F4），如圖1所示。進口道機動車相位和環道機動車相位采用的交通信號燈具均為圓形信號燈。歸屬于不同相位的道路使用者的交通沖突關系，如圖2所示。存在交通沖突的相位不允許同時獲得通行權。

2.2 相位組合方案

相位組合方案用以描述一系列允許同步獲得通行權的相位（或稱并發相位）的組合關系，體現了一種相對穩定的通行時間資源供給狀態。任意一個相位應至少存在于一個相位組合方案之中。

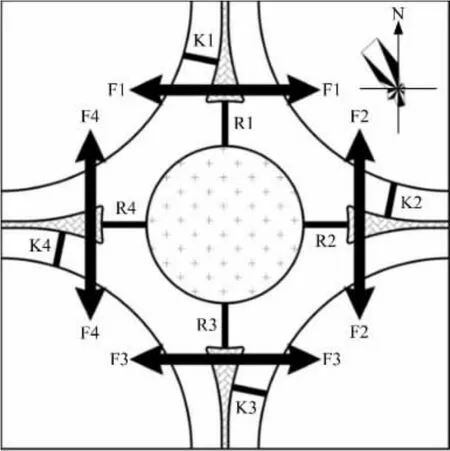
圖1 相位編號Fig.1 Phase numbering

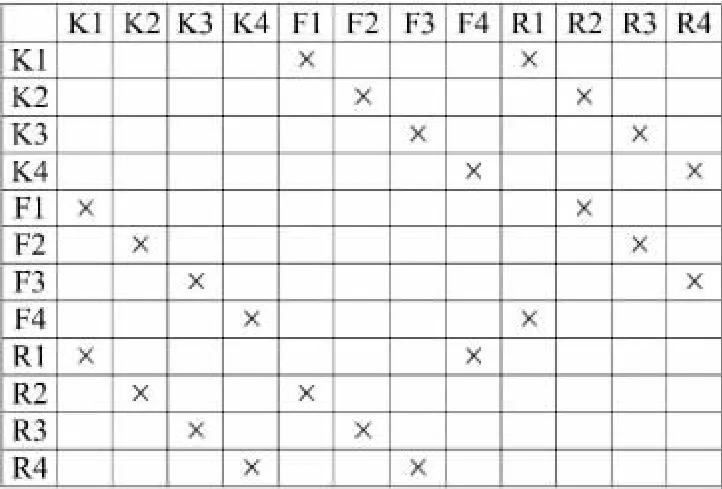
圖2 交通沖突關系Fig.2 Traffic conflicts matrix

單進口輪流放行方式下，四路環形交叉口可能產生8種常規相位組合方案，如圖3所示。進口道機動車相位與逆時針方向相鄰的第1個行人相位同步獲得通行權。進口道機動車相位的綠燈期間，為了充分利用局部環道的通行空間資源，允許順時針方向相鄰的第1個進口道機動車相位獲得通行權。

2.3 相位顯示順序

相位顯示順序用以描述不同相位組合方案之間的更迭關系，實質上反映了沖突相位之間的通行權傳承順序，是相位結構設計的集中表現形式。

單進口輪流放行方式下，四路環形交叉口采用的常規相位顯示順序如圖4所示。按照逆時針順序，依次為各個進口道機動車相位賦予通行權。

2.4 通行權供給的時間特性

通行權供給的時間特性是對交叉口可能采用的相位顯示順序中隱含的、關于通行時間資源供給的結構性特征的歸納和總結。根據常規相位顯示順序，得到以下4項通行權供給的時間特性:

（1）進口道機動車相位與緊鄰的環道機動車相位存在直接的通行權傳承關系，它們的綠燈顯示時間加上綠燈間隔時間之和始終等于信號周期時間，即:

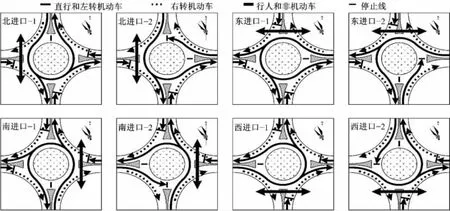
圖3 常規相位組合方案Fig.3 Common phase combinations

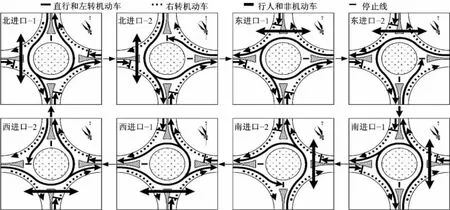
圖4 常規相位顯示順序Fig.4 Common phase sequence

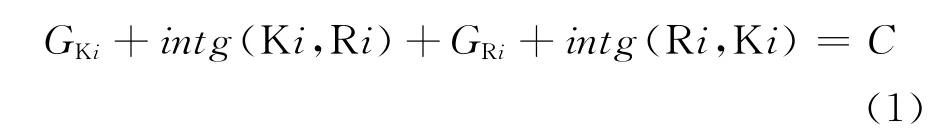
（2）進口道機動車相位的綠燈顯示時間與信號周期時間的數值關系如圖5所示，數學表達式為:

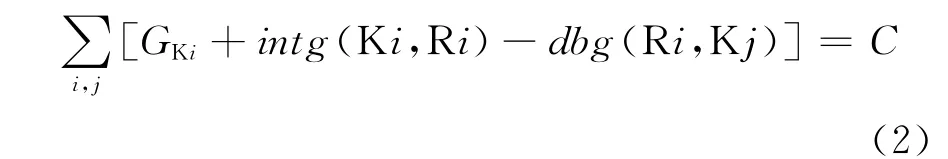
（3）根據相位顯示順序和交通沖突關系，利用式（3）（4）（5）計算進口道機動車相位、環道機動車相位的綠燈啟亮和結束時刻。

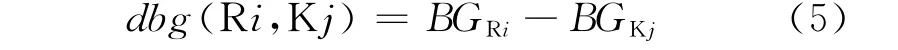
（4）根據相位顯示順序和交通沖突關系，利用式（6）（7）計算行人相位的綠燈啟亮和結束時刻:

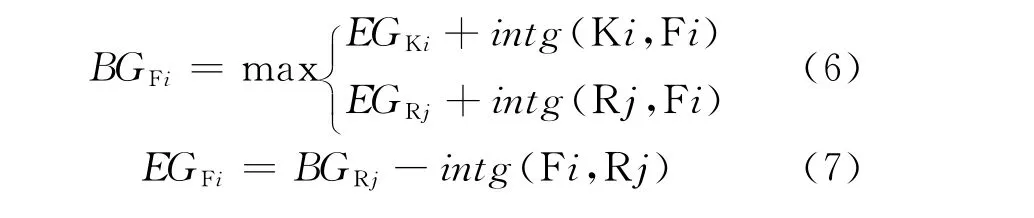
3 信號配時設計

信號配時設計的目的是基于平面交叉口的道路空間條件和相位顯示順序，根據通行權供給的時間特性以及控制時段內的通行時間資源需求水平，遵循一定的原則和步驟，采用一定的方法，計算信號周期時間以及各個相位、各種信號燈色的啟亮和結束時刻，實現通行時間資源的戰術分配。

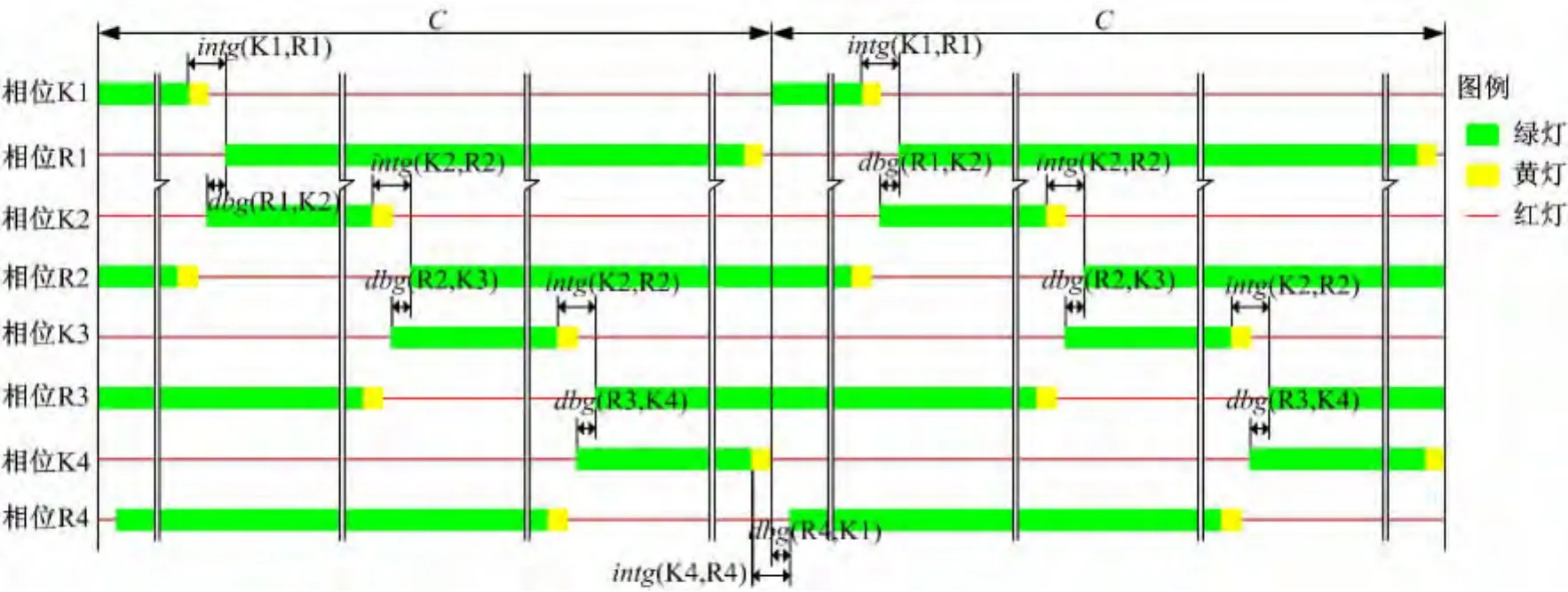
圖5 GKi與C的數值關系Fig.5 Numerical relationship between GKiand C

3.1 進口道機動車相位的通行時間資源需求

設計流率表征了進口道機動車相位可能承載的最大通行需求。給定設計流率下，進口道的通行條件越好，飽和流率越高，滿足通行需求所需的綠燈顯示時間理應越少。可以利用設計流率與飽和流率的比值（即流率比）表征進口道機動車相位可能承載的最大通行需求水平。流率比的引入使得不同進口道機動車相位對于通行時間資源的原始需求具備了橫向可比性。

設計飽和度是針對各個進口道機動車相位設定的最大允許飽和度，表征了該相位通行能力的期望富余程度。不同進口道機動車相位的設計飽和度可以不同。給定流率比下，設計飽和度越高，通行能力的期望富余程度越低，進口道機動車相位獲得的綠燈顯示時間越少。設計飽和度的建議取值為0.80、0.85、0.90、0.95。可以利用流率比與設計飽和度的比值表征進口機動車相位可能承載的最大通行時間資源需求水平，并將其作為信號配時設計的主要依據。流率比與設計飽和度的比值的引入使得不同進口道機動車相位對于通行時間資源的設計需求具備了橫向可比性。

3.2 進口道機動車相位的綠燈早啟時間

根據入環車輛（特指左轉和直行車輛）的交通運行特性，進口道機動車相位的綠燈啟亮后，入環車輛將以車隊的形式進入環道；入環車隊的頭車一旦受到環道信號燈的阻滯，后續車輛將依次受到阻滯效應的影響，或減速、或停車；環道信號燈的綠燈啟亮后，入環車隊的頭車及后續車輛依次加速至期望車速，環道信號燈對于入環車隊的阻滯效應逐漸消失。

相對于逆時針方向相鄰的第1個環道機動車相位，進口道機動車相位的綠燈早啟時間應允許入環車隊的頭車經歷一定的阻滯時間，同時，應確保阻滯效應不會傳遞至進口道停止線斷面（即入環車輛通過進口道停止線時不會受到前方車輛的阻滯而減速或停車）。利用式（8）計算進口道機動車相位與逆時針方向相鄰的第1個環道機動車相位的綠燈啟亮時間差:

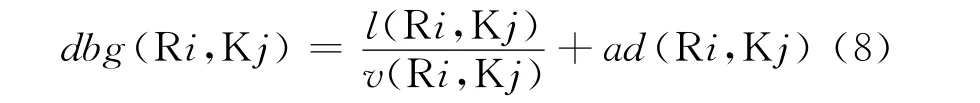
3.3 進口道機動車相位的綠燈顯示時間

假定進口道機動車相位的綠燈前損失時間等于綠燈后補償時間，即有效綠燈時間等于綠燈顯示時間。對于任意給定的信號周期時間，利用式（2）（8）計算進口道機動車相位的綠燈顯示時間總和，利用式（9）計算各個進口道機動車相位的綠燈顯示時間:

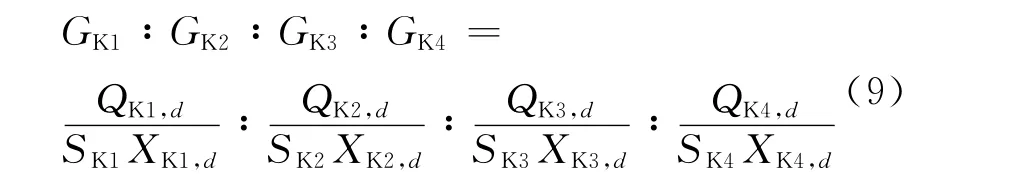
3.4 行人相位的最小綠燈顯示時間

設置行人過街中央安全島后，人行橫道被分為兩段，可以實施行人“同步二次過街”控制［11］。較高機動車交通負荷水平下，行人相位的最小綠燈顯示時間應保證綠燈初期進入人行橫道的行人能夠到達另一段人行橫道的中央位置。

3.5 進口道機動車相位的最小綠燈顯示時間

與普通平面交叉口類似，進口道機動車相位的最小綠燈顯示時間應保證行車安全、一定數量的入環車輛順利通過進口道停止線以及行人和非機動車安全過街，見式（10）［12－14］:

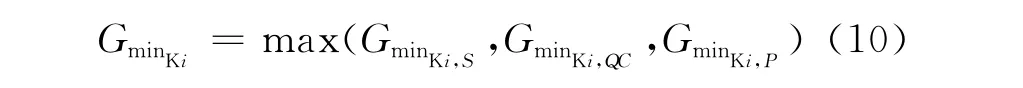
式中:GminKi，S和GminKi，QC通常取為經驗值，GminKi，P的數值與多種因素密切相關。根據通行權供給的時間特性，以相位Rj的綠燈結束時刻為起點、綠燈啟亮時刻為終點，劃定GminKj，P與GminFi的數值關系分析區間，如圖6所示，數學表達式見式（11）。將式（12）（13）帶入式（11），得到進口道機動車相位的最小綠燈顯示時間。

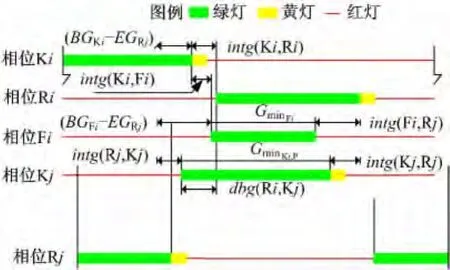
圖6 GminKj，P與GminFi的數值關系Fig.6 Numerical relationship between GminKj，P and GminFi

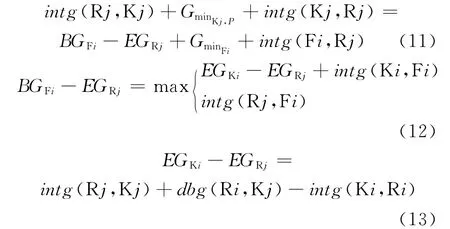
3.6 信號周期時間邊界值

最大信號周期時間的取值不宜超過150s。將進口道機動車相位的綠燈顯示時間取為該相位的最小綠燈顯示時間，利用式（2）得到最小信號周期時間的計算方法，見式（14）:

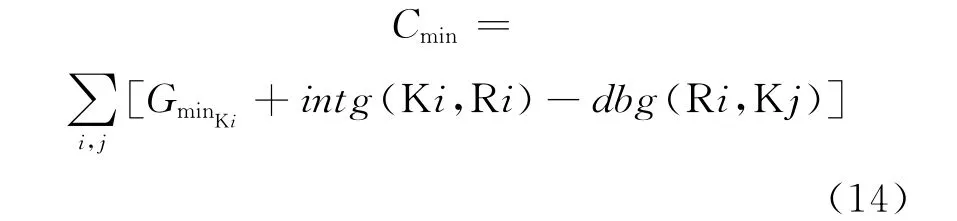
3.7 最佳信號周期時間

將最佳信號周期時間定義為根據通行權供給的時間特性，在信號周期時間邊界值、進口道機動車相位的最小綠燈顯示時間和設計飽和度的共同約束下，能夠滿足所有道路使用者的通行時間資源需求的最小信號周期時間。

與以往研究不同的是，本方法并未建立最佳信號周期時間的計算公式，而是要求自最小信號周期時間開始，直至最大信號周期時間，針對每個可能的信號周期時間取值，計算各個進口道機動車相位的綠燈顯示時間和理論飽和度，將首先滿足進口道機動車相位的最小綠燈顯示時間和設計飽和度約束的信號周期時間視為最佳信號周期時間。因此，最終確定的最佳信號周期時間需要經過多輪試算，試算結果應保留小數點后1位有效數字并進行4舍5入取整操作。

若所有可能的信號周期時間取值均不滿足約束條件，認為在當前的通行空間資源供給條件下，本方法無法為所有的道路使用者提供足夠的通行時間資源，只能終止信號配時設計。必須通過調整交通流向和流線組織以及交通標志和標線設計，改變環形交叉口的通行空間資源供給條件，方能重新進行信號配時設計。

信號配時設計的技術流程如下:

步驟1:確定ad（Ri，Kj），利用式（8）計算dbg（Ri，Kj），執行步驟2。

步驟2:確定GminFi，利用式（11）（12）（13）計算GminKj，P，執行步驟3。

步驟3:確定GminKi，S、GminKi，QC，利用式（10）計算GminKi，執行步驟4。

步驟4:利用式（14）計算Cmin，令t＝1；C（t）o＝Cmin，執行步驟5。

步驟5:若C（t）o≤Cmax，利用式（2）（9）計算G（t）K1、G（t）K2、G（t）K3、G（t）K4，執行步驟6；否則，執行步驟8。

步驟6:若G（t）Ki≥GminKi且X（t）Ki≥XKi，d，令Co＝C（t）o；GKi＝G（t）Ki，執行步驟7；否則，令t＝t＋1；C（t）o＝C（t）o＋1，執行步驟5。

步驟7:令BGK1＝0，利用式（3）～ （7）計算BGKi、EGKi、BGRi、EGRi、BGFi、EGFi，生成信號配時方案。

步驟8:調整交通流向和流線組織以及交通標志和標線設計，執行步驟1。

顯然，本方法并未采用優化建模的思想，即通過對充滿隨機性、時變性和不確定性的道路交通系統進行一定程度的簡化和抽象，將環形交叉口的通行時間資源分配問題描述成交通信號控制參數的約束優化問題，而是采用了非優化建模的思想，致力于認清道路使用者的交通運行特性，發現通行時間資源供給的結構性特征，匹配通行時間資源的供求關系，在必要的約束條件下，以一種確定性的方式，分層次、分步驟地確定交通信號控制參數，這使得本方法不僅具有科學性，還具備較強的環境適應能力，更加簡單、易用。

4 仿真實驗分析

選取典型的四路環形交叉口，在中等和較低機動車交通負荷水平下，實施讓行規則控制，在較高機動車交通負荷水平下，實施單進口輪流放行方式的交通信號控制。

利用VISSIM 5.3建立仿真實驗環境，測試和分析對象交叉口的性能。

4.1 道路空間條件

對象交叉口的道路空間條件如圖7所示。南北方向為主要道路，東西方向為次要道路。各條道路的路段車道數均為3條，各個進口方向具有相同的車道功能，即1條右轉專用車道、2條直行專用車道、1條左轉調頭合用車道。

進口道采用右側展寬，最外側進口道的展寬段長度為50m，展寬漸變段的長度為20m。

中心島的直徑為35m，進口道、出口道、環道的寬度分別為3m／ln、3.5m／ln、4m／ln，人行橫道的寬度為5m，非機動車過街通道的寬度為3 m。

圖7 道路空間條件Fig.7 Road geometric condition

路段和進出口道的限制車速均為50km／h。直行專用進口道和左轉調頭合用進口道的飽和流率均為1800pcu／（h·ln）。取l（Ri，Kj）≈51m，v（Ri，Kj）＝40km／h。

4.2 交通需求條件

較低、中等、較高機動車交通負荷水平下，分別在一定的抽樣范圍內隨機選取3組機動車到達交通量，如表1所示。人行橫道的單向過街行人交通量分別為100、200、400ped／h；非機動車過街通道的單向過街非機動車交通量分別為50、100、200cyc／h。

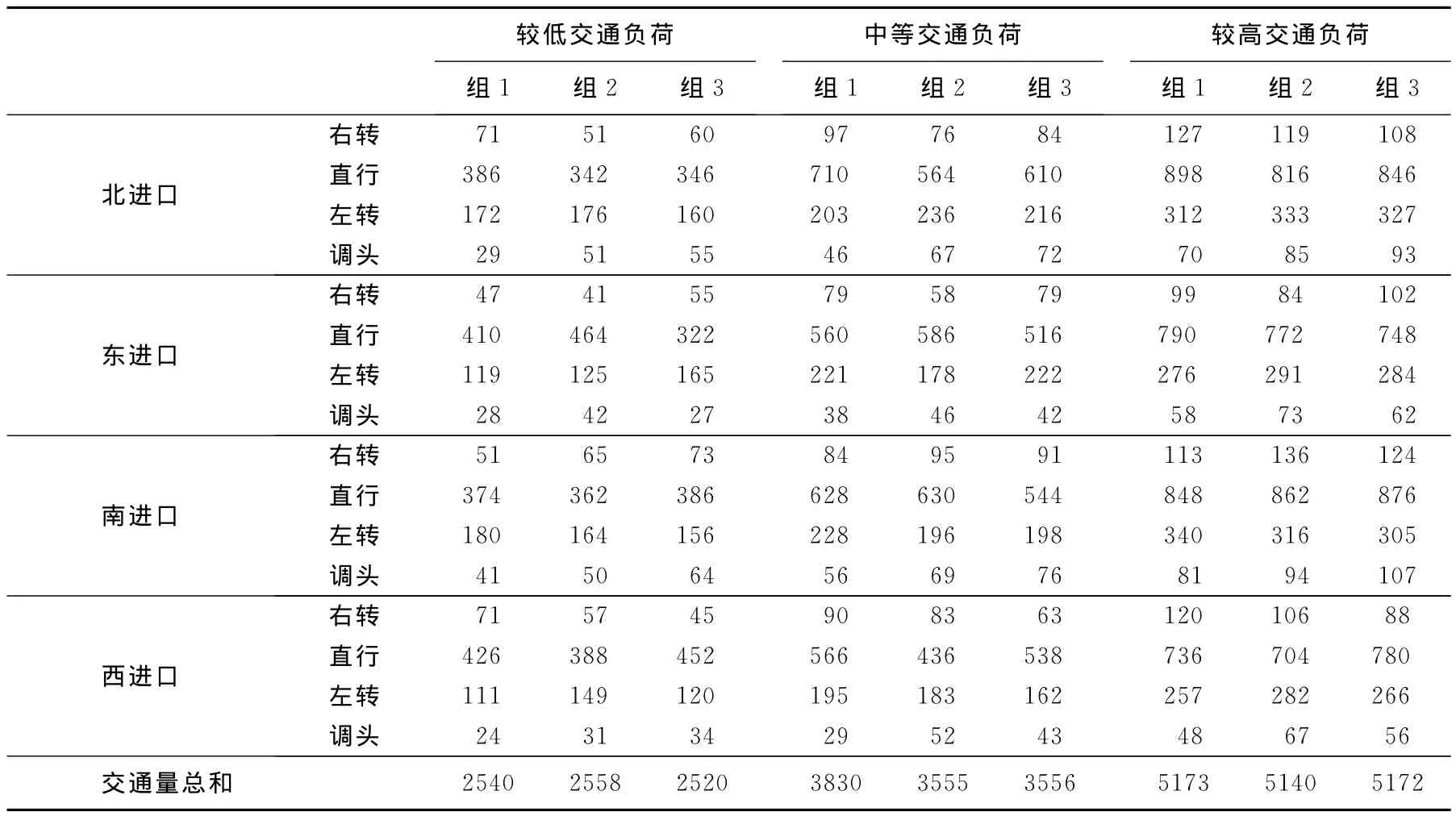
表1 機動車到達交通量的抽樣結果Table 1 Sampling results of vehicular demands pcu／h

較高機動車交通負荷水平下，各個進口方向選取車道平均機動車到達量的最大值作為進口道機動車相位的設計流率。在此基礎上，得到進口道機動車相位的流率比如表2所示。

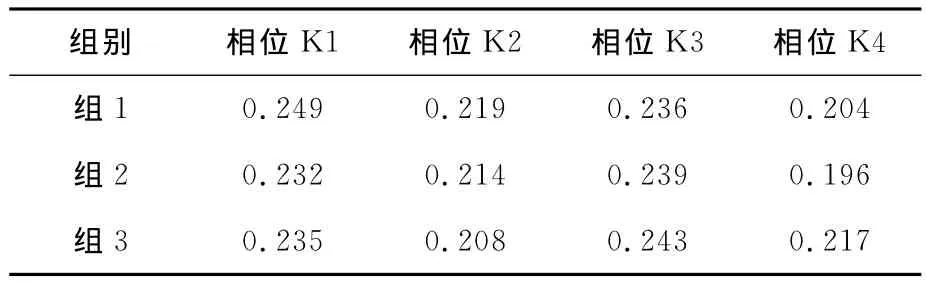
表2 進口道機動車相位的流率比Table 2 Flow ratios of entering vehicle phases

4.3 信號控制條件

進口道機動車相位和環道機動車相位的黃燈時間均為3s。對象交叉口的綠燈間隔時間如圖8所示。

較高機動車交通負荷水平下，令GminFi＝18s；GminKi，S＝10s；GminKi，QC＝15s，利用式（10）～（14）得到GminKi＝24s。令 XK1，d＝XK3，d＝0.9；XK2，d＝XK4，d＝0.95；ad（Ri，Kj）＝2s。以相位 K1的綠燈啟亮時刻作為信號周期時間的起點，不同交通需求條件下的信號配時方案如表3所示。

4.4 仿真模型參數

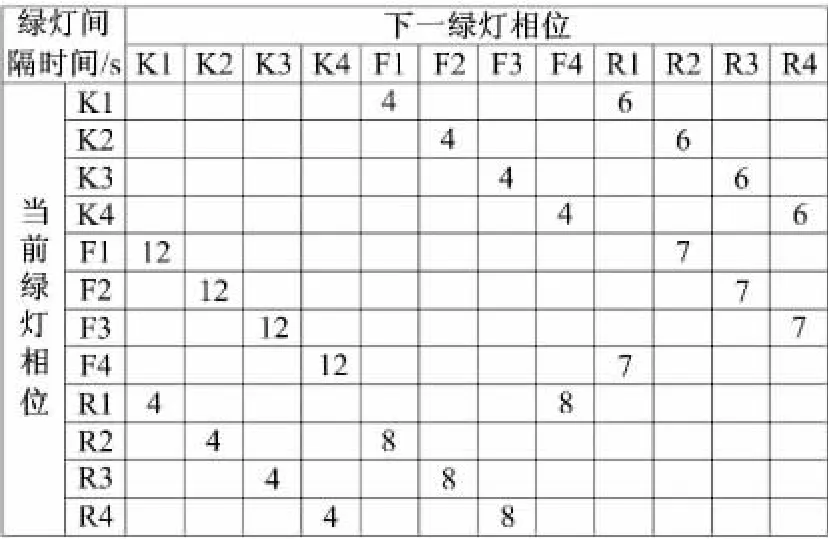
圖8 綠燈間隔時間Fig.8 Intergreen time matrix

為了消除標準車輛折算給仿真建模帶來的不便，將機動車的交通構成視為標準車輛（即車輛長度小于6m的小型車）。

機動車的最小和最大期望速度分別為48和58km／h。行人的最小和最大期望速度為4和6 km／h。非機動車的最小和最大期望速度為12和15km／h。

車輛跟馳模型中，平均停車間距為2.0m，期望安全距離的附加部分為2.5m，期望安全距離的倍數部分為3.5m。車道變換模型中，車輛消失前的等待時間為45s。其他駕駛行為參數采用默認值。

表3 信號配時方案Table 3 Signal timing plans

仿真運行總時間為10800s，實驗數據采集時段為900～10800s。針對每組交通需求進行一組仿真實驗，每組仿真實驗進行5次仿真運行，每次仿真運行選取的隨機數分別為9、19、29、39、49。

4.5 仿真實驗結果

選取交叉口的車均延誤、交叉口的車均停車次數、各個進口方向的車均延誤極差作為機動車相位的性能指標，選取行人和非機動車的人均延誤作為行人相位的性能指標。每組交通需求下的性能指標值取為5次，仿真運行得到該性能指標值的算術平均值。仿真實驗結果如表4所示。

較低機動車交通負荷水平下，對象交叉口的各項性能指標值均處于低位運行態勢。中等機動車交通負荷水平下，各項性能指標值均顯著增大，對象交叉口的整體性能趨于惡化的態勢已經形成，若不及時提升交通控制等級，局部環道乃至整個交叉口陷入死鎖狀態將在所難免。

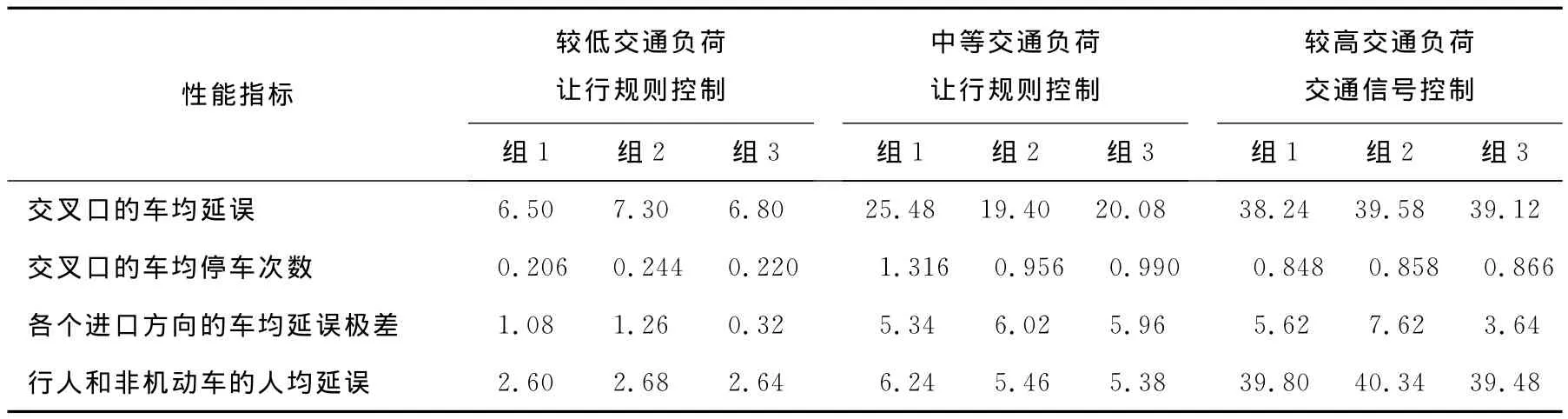
表4 仿真實驗結果Table 4 Simulation test results

較高機動車交通負荷水平下，隨著對象交叉口的交通控制等級由讓行規則控制提升至交通信號控制，交叉口的車均延誤顯著增大，但交叉口的車均停車次數和各個進口方向的車均延誤極差得到了有效控制，說明本文提出的交通信號控制方法不僅能夠避免機動車的通行效率再度降低，還能夠均衡不同進口道機動車相位的性能；與讓行規則控制相比，行人和非機動車的人均延誤出現大幅增加是實施交通信號控制的必然結果，但是，本文提出的交通信號控制方法可以將人均延誤值控制在一個相對較低的水平。

5 結束語

就環形交叉口的交通控制方法而言，讓行規則控制適用于機動車交通低峰和平峰時段；交通信號控制適用于機動車交通高峰時段。對于交通信號控制環形交叉口，單進口輪流放行方式具有更為普遍的適用性，找到一種科學、有效的交通信號控制方法是促使其推廣應用的重要前提。本文面向四路環形交叉口，以安全、高效地實施單進口輪流放行方式的交通信號控制為基本目的，通過深入剖析道路使用者的交通運行特性、通行時間資源供給的結構性特征、通行時間資源的供求關系，建立了相位結構設計方法和信號配時設計方法，較為系統地解決了通行時間資源的戰略和戰術分配問題。仿真實驗結果顯示，隨著機動車交通負荷水平的提高，讓行規則控制將難以遏制環形交叉口整體性能的顯著惡化，本文提出的交通信號控制方法具有科學性、有效性、實用性，有助于顯著改善機動車交通高峰時段環形交叉口的整體性能。

［1］Federal Highway Administration.Roundabouts:an informational guide［R］.Turner Fairbank Highway Research Center:McLean，VA，2000.

［2］Brabander B，Vereeck L.Safety effects of roundabouts in Flanders:signal type，speed limits and vulnerable road users［J］.Accident Analysis and Prevention，2007，39（3）:591－599.

［3］Daniels S，Nuyts E，Wets G.The effects of roundabouts on traffic safety for bicyclists:an observational study［J］.Accident Analysis and Prevention，2008，40（2）:518－526.

［4］Akcelik R.Roundabout metering signals:capacity，performance and timing［C］∥The 6th International Symposium on Highway Capacity and Quality of Service，Stockholm，Sweden，2011.

［5］Lu G，Guan F，Noyce D.Simulation study of access management at modern roundabouts［J］.Transportation Research Record，2011，2265:209－225.

［6］Schroeder B，Rouphail N，Hughes R.Toward roundabout accessibility－exploring the operational impact of pedestrian signalization options at modern roundabouts［J］.ASCE Journal of Transportation Engineering，2008，134（6）:262－271.

［7］Yang X G，Li X G，Xue K.A new traffic signal control for modern roundabouts:method and application［J］.IEEE Transactions on Intelligent Transportation Systems，2004，5（4）:282－287.

［8］薛昆，楊曉光，白玉.給定周期條件下環型交叉口優化控制方法研究［J］.公路交通科技，2004，21（5）:83－87.Xue Kun，Yang Xiao－guang，Bai Yu.Optimization of control method for roundabout at fixed cycle［J］.Journal of Highway and Transportation Research and Development，2004，21（5）:83－87.

［9］楊曉光，趙靖，汪濤.環形交叉口信號控制最佳周期計算方法［J］.中國公路學報，2008，21（6）:90－95.Yang Xiao－guang，Zhao Jing，Wang Tao.Optimal cycle calculation method of signal control at roundabout［J］.China Journal of Highway and Transport，2008，21（6）:90－95.

［10］趙靖，郁曉菲，白玉，等.十字環形交叉口兩種信號控制設計方法比較［J］.長沙交通學院學報，2008，24（3）:53－58.Zhao Jing，Yu Xiao－fei，Bai Yu，et al.Comparison between two methods of signal design for cross roundabouts［J］.Journal of Changsha Communica－tions University，2008，24（3）:53－58.

［11］李克平.交通信號控制指南——德國現行規范（RiLSA）［M］.北京:中國建筑工業出版社，2006.

［12］徐洪峰，耿現彩.面向T形交叉口的機動車相位固定最小綠燈時間計算［J］.吉林大學學報:工學版，2012，42（3）:600－605.Xu Hong－feng，Gen Xian－cai.Absolute minimum green time calculation for vehicles at 3－leg intersection［J］.Journal of Jilin University（Engineering and Technology Edition），2012，42（3）:600－605.

［13］徐洪峰，鄭明明，李克平.機動車相位固定最小綠燈時間計算方法［J］.公路交通科技，2008，25（5）:105－110.Xu Hong－feng，Zheng Ming－ming，Li Ke－pin.Absolute minimum green time calculation for vehicle phase［J］.Journal of Highway and Transportation Research and Development，2008，25（5）:105－110.

［14］徐洪峰，王殿海.BRT優先控制交叉口的機動車相位固定最小綠燈時間計算方法［J］.吉林大學學報:工學版，2009，39（增刊1）:92－97.Xu Hong－feng，Wang Dian－hai.Absolute minimum green calculation for vehicle phase at signalized intersections with bus rapid transit signal priority［J］.Journal of Jilin University（Engineering and Technology Edition），2009，39（Sup.1）:92－97.