多重參數(shù)區(qū)間軟集

許宏偉， 劉衛(wèi)鋒

(鄭州航空工業(yè)管理學(xué)院 數(shù)理系，河南 鄭州 450015)

多重參數(shù)區(qū)間軟集

許宏偉， 劉衛(wèi)鋒

(鄭州航空工業(yè)管理學(xué)院 數(shù)理系，河南 鄭州 450015)

將區(qū)間軟集與多重參數(shù)軟集相結(jié)合，提出了一種新的軟集——多重參數(shù)區(qū)間軟集，推廣了多重參數(shù)軟集和區(qū)間軟集.然后，研究了多重參數(shù)區(qū)間軟集的基本運(yùn)算和性質(zhì).最后，給出多重參數(shù)區(qū)間軟集在決策中的一個(gè)應(yīng)用實(shí)例.

軟集；區(qū)間軟集；多重參數(shù)軟集；多重參數(shù)區(qū)間軟集；決策

1999年，Molodtsov在文[1]中提出了軟集的概念，試圖從參數(shù)化的角度為研究不確定性問(wèn)題提供統(tǒng)一的數(shù)學(xué)框架，由于軟集與模糊集、粗糙集等不確定性理論具有很強(qiáng)的互補(bǔ)性，因此受到了許多學(xué)者的關(guān)注和研究,并且成為不確定性理論研究的一個(gè)熱點(diǎn).目前，關(guān)于軟集的研究已經(jīng)取得了一系列的研究成果，其中，文[2-4]對(duì)軟集的基本運(yùn)算等進(jìn)行了研究，完善了軟集的運(yùn)算體系,文[5-9]將模糊集理論與軟集相結(jié)合，分別提出了模糊軟集、區(qū)間模糊軟集、Vague集軟集、直覺模糊軟集和區(qū)間值直覺模糊軟集,文[10,11]通過(guò)將軟集和模糊軟集的參數(shù)集由經(jīng)典集推廣到模糊集，定義了具有模糊化參數(shù)的軟集和模糊軟集，文[12]在考慮多重參數(shù)的情況下，提出了多重參數(shù)軟集，文[13-15]在文[16]基礎(chǔ)上，提出了區(qū)間軟集，進(jìn)一步推廣了軟集,文[17-23]研究了軟集和模糊軟集在決策中的應(yīng)用.

在上述研究基礎(chǔ)上，本文將文[12]中的多重參數(shù)軟集與文[13-15]中的區(qū)間軟集相結(jié)合，提出了多重參數(shù)區(qū)間軟集的概念，使得多重參數(shù)軟集和區(qū)間軟集成為其特例，從而推廣了軟集的概念.然后，定義和研究了多重參數(shù)區(qū)間軟集的基本運(yùn)算和性質(zhì).最后，通過(guò)一個(gè)實(shí)例說(shuō)明多重參數(shù)區(qū)間軟集在決策中的應(yīng)用.

1 相關(guān)概念

定義1.1[1]設(shè)U是論域，P(U)是其冪集，E是一個(gè)參數(shù)集，A?E.若F:A→P(U)，則稱(F,A)為U上的一個(gè)軟集.

定義1.3[12]設(shè)(F，A)和(G，B)是U上兩個(gè)多重參數(shù)軟集，稱(F，A)是(G，B)的多重參數(shù)軟子集，如果(1)A?B, (2)?x∈A,F(x)?G(x).

定義1.4[12]設(shè)(F,A)和(G,B)是U上兩個(gè)多重參數(shù)軟集，如果(F,A)是(G,B)的多重參數(shù)軟子集，且(G,B)是(F,A)的多重參數(shù)軟子集，那么稱(F,A)與(G,B)相等.

定義1.5[12]設(shè)E={e1,e2,L,en}是一個(gè)參數(shù)集，則E的否定集定義并表示為E,，E={e1,e2,L,en}，其中ei為非ei.

稱為區(qū)間集,這里Al?Au.

定義1.7[13-15]設(shè)U是論域，E是指標(biāo)集，A?E，F(xiàn)：A→IP(U)是一個(gè)映射，稱(F,A)是U上的一個(gè)區(qū)間軟集，其中IP(U)表示U上的所有區(qū)間集.

IP(U)上的偏序關(guān)系≤定義為：

[Al,Au],[Bl,Bu]∈IP(U),[Al,Au]≤[Bl,Bu]?Al?Bl,Au?Bu.

定義1.8[13-15]設(shè)(F1,A1),(F2,A2)是U上的兩個(gè)區(qū)間軟集，則定義區(qū)間軟集的運(yùn)算如下：

(2)(F,A)=(F1,A1)U%(F2,A2),其中A=A1∪A2，

(3)(F,A)=(F1,A1)∩(F2,A2),其中A=A1∩A2，?x∈A,F(x)=F1(x)∩F2(x).

(4)(F,A)=(F1,A1)∧(F2,A2),其中A=A1×A2,?(x,y)∈A1×A2, H(x,y)=F1(x)∩F2(y).

2 多重參數(shù)區(qū)間軟集

定義2.1若F：A→IP(U)，則稱(F,A)為U上的一個(gè)多重參數(shù)區(qū)間軟集.

E2={e21,e22}，E3={e31,e32,e33,e34}，A?E,且A=a1={e11},a2={e11,e21},a3={e11,e21,e31},

a4={e12,e32},a5={e13,e22,e34}}，且F(a1)=[{u1,u2},{u1,u2,u4}],F(a2)=[Φ,{u1,u3}],

F(a3)=[{u2,u3},{u2,u3,u5,u6}],F(a4)=[{u3,u4},{u2,u3,u4}],F(a5)=[{u2,u3,u4},U].

則多重參數(shù)區(qū)間軟集表示為:

(F,A)={(a1,[{u1,u2},{u1,u2,u4}]),(a2,[Φ,{u1,u3}]),(a3,[{u2,u3,},{u2,u3,u5,u6}])，

(a4,[{u3,u4},{u2,u3,u4}]),(a5,[{u2,u3,u4},U]).

例2.2 在例2.1中，假設(shè)B={a1={e11},a2={e11,e21},a3={e11,e21,e31},a4={e12,e32},a5={e13,e22,e34},a6={e12,e21,e33}},且G(a1)=[{u1,u2},{u1,u2,u3,u4},G(a2)=[{u3},{u1,u3,u4}],G(a3)=[{u2,u3,u4},{u1,u2,u3,u5,u6}]，G(a4)=[{u2,u3,u4},U],G(a5)=[{u2,u3,u4,u6},U],G(a6)=[{u3},{u2,u3,u6}].

定義2.4多重參數(shù)區(qū)間軟集(F，A)的補(bǔ)集(F，A)c定義為(F,A)c=(Fc，A)其中Fc:A→IP(U)，F(xiàn)c(a)=[U,U]-F(a),?a∈A,A?P(E).

例2.3 多重參數(shù)區(qū)間軟集為例2.1中的(F，A)，則

(F，A)c={(a1,[{u3,u5,u6},{u3,u4,u5,u6}]),(a2,[{u2,u4,u5,u6},U]),

(a3,[{u1,u4},{u1,u4,u5,u6}]),(a4,[{u1,u5,u6},{u1,u2,u5,u6}]),(a5,[Φ,{u1,u5,u6}]).

定理2.1設(shè)(F，A)為論域U上的多重參數(shù)區(qū)間軟集，則((F，A)c)c=(F,A).

證明：由定義2.4知，F(xiàn)c:A→IP(U)，其中Fc(a)=[U,U]-F(a),?a∈A,A?P(E).而(Fc)c:(A)→IP(U)，其中(Fc)c(a)=[U,U]-Fc((a)),?a∈(A),(A)?(P(E)).由于(A)=A,(a)=a,(A)=A,(P(E))=P(E),因此有(Fc)c:A→IP(U)，其中(Fc)c(a)=[U,U]-Fc(a)=F(a),?a∈A,A?P(E)，即((F,A)c)c=(F,A).

定義2.5設(shè)(F,A)(G,B)為論域U上的兩個(gè)多重參數(shù)區(qū)間軟集，則它們的并定義為：

定理2.2設(shè)(F，A)，(G，B)，(H，C)為論域U上的多重參數(shù)區(qū)間軟集，則

證明：顯然.

定義2.6設(shè)(F，A)，(G，B)為論域U上的兩個(gè)多重參數(shù)區(qū)間軟集，則它們的交定義為：

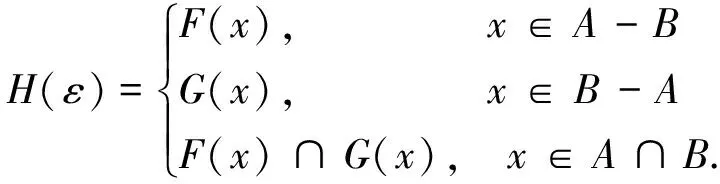
定理2.3設(shè)(F，A)，(G，B)，(H，C)均為論域U上的多重參數(shù)區(qū)間軟集，則

證明：顯然.

定理2.4設(shè)(F,A),(G,B),(H,C)均為論域U上的多重參數(shù)區(qū)間軟集，則

證明：略.

定義2.7設(shè)(F,A),(G,B)為論域U上的兩個(gè)多重參數(shù)區(qū)間軟集，則它們的與定義為(F,A)∧(G,B)=(H,A×B),其中H(x,y)=F(x)∩G(y),?(x,y)∈A×B.

定義2.10設(shè)(F,A),(G,B)為論域U上的兩個(gè)多重參數(shù)區(qū)間軟集，則它們的或定義為(F,A)∨(G,B)=(H,A×B)，其中H(x,y)=F(x)∪G(y),?(x,y)∈A×B.

定理2.5設(shè)(F，A)，(G，B)為論域U上的多重參數(shù)區(qū)間軟集，則

((F,A)∧(G,B))c=(F,A)c∨(G,B)c,((F,A)∨(G,B))c=(F,A)c∧(G,B)c.

證明：略.

定理2.6設(shè)(F,A),(G,B),(H,C)為論域U上的多重參數(shù)區(qū)間軟集，則

((F,A)∧(G,B))∧(H,C)=(F,A)∧((G,B)∧(H,C))，

((F,A)∨(G,B))∨(H,C)=(F,A)∨((G,B)∨(H,C))，

(F,A)∨((G,B)∧(H,C))=((F,A)∨(G,B))∧((F,A)∨(H,C))，

(F,A)∧((G,B)∨(H,C))=((F,A)∧(G,B))∨((F,A)∧(H,C)).

證明：略.

3 決策應(yīng)用

由于多重參數(shù)區(qū)間軟集的參數(shù)為多個(gè)不同方面參數(shù)的組合，因此它更能體現(xiàn)出軟集的優(yōu)點(diǎn)，但是我們只要將每一種參數(shù)組合視為一個(gè)參數(shù)，則多重參數(shù)區(qū)間軟集就仍然可以看做是一種區(qū)間軟集.為此，我們借助文獻(xiàn)[15]方法，給出利用多重參數(shù)區(qū)間軟集進(jìn)行決策的一種方法.具體步驟如下：

步驟1 根據(jù)實(shí)際情況建立多重參數(shù)區(qū)間軟集(F，A)；

步驟2 將多重參數(shù)區(qū)間軟集(F，A)的每個(gè)組合參數(shù)看做一個(gè)參數(shù)，建立多重參數(shù)區(qū)間軟集的表格形式.表格中元素uij確定如下[15]：

對(duì)于?a∈A,F(a)=[F-(a),F+(a)]，顯然，F(xiàn)-(a)中元素必屬于F(a),U-F+(a)，中元素必不屬于F(a)，而F+(a)-F-(a)中元素可能屬于F(a).于是，元素uij定義如下：

若uj∈F-(a)，則uij=1；若uj∈U-F+(a)，則uij=0；若uj∈F+(a)-F-(a)，則uij=*，其中uij=*表示我們不確定uj是否屬于F(a).

步驟3 建立多重參數(shù)區(qū)間軟集的拓展表格形式；

(F，A)={(a1,[h2,h3,h7,h10},{h2,h3,h6,h7,h10}]),(a2,[{h6,h7},{h1,h6,h7,h8}]),(a3,Φ),

(a4,[{h1,h8,h9},{h1,h8,h9,h10}]),(a5,[{h8},{h1,h7,h8}]),(a6,Φ),(a7,[{h9},{h1,h8,h9}])}

請(qǐng)利用多重參數(shù)區(qū)間軟集幫助購(gòu)房人選購(gòu)合適的房子.

步驟1 建立多重參數(shù)區(qū)間軟集的表格形式，見表1.

表1 多重參數(shù)區(qū)間軟集的(拓展)表格形式Table 1 (Extended)Tabular representation of multiparameterized interval soft set

步驟2 建立多重參數(shù)區(qū)間軟集的拓展表格形式，其中*后面括號(hào)內(nèi)元素為F+(a)-F-(a)中元素屬于F(a)的概率表示Pa，見表1.

[1] MOLODTSOV D. Soft set theory-first results[J]. Computers and Mathematics with Applications,1999,37:19-31.

[2] MAJI P K, BISWAS R, ROY A R. Soft set theory[J]. Computers and Mathematics with Applications,2003,45:555-562.

[3] ALI M I, FENG F, LIU X, et al. On some new operations in soft set theory[J]. Computers and Mathematics with Applications,2009,57:1547-1553.

[4] QIN K, HONG Z. On soft equality[J]. Journal of Computational and Applied Mathematics,2010,234:1347-1355.

[5] MAJI P K, BISWAS R, ROY A R. Fuzzy soft sets[J]. The Journal of Fuzzy Mathematics,2001,9(3):589-602.

[6] YANG X B, LIN T Y, YANG J Y. Combination of interval-valued fuzzy set and soft set[J]. Computers and Mathematics with Applications,2009,58:521-527.

[7] XU W, MA J, WANG S, HAO G. Vague soft sets and their properties[J].Computers and Mathematics with Applications, 2010,59:787-794.

[8] MAJI P K, BISWAS R, ROY A R. Intuitionistic fuzzy soft sets[J].The Journal of Fuzzy Mathematics, 2001,9:677-691.

[9] JIANG Y, TANG Y, CHEN Q, LIUH, TANG J. Interval-valued intuitionistic fuzzy soft sets and their properties[J]. Computers and Mathematics with Applications,2010,60:906-918.

[10] CAGMAN N, CITAK F, ENGINOGLU S. FP-soft set theory and its applications[J]. Annals of Fuzzy Mathematics and Informatics, 2011,2(2):219-226.

[11] CAGMAN N, CITAK F, ENGINOGLU S. Fuzzy parameterized fuzzy soft set theory and its applications[J]. Turkish Journal of Fuzzy Systems, 2010,1(2):21-35.

[12] ABDUL R S, SHAWKAT A, NASRUDDIN H, ABD G A. Multiparameterized soft set[J]. Journal of Mathematics and Statistics,2012,8(1):92-97.

[13] 付清.模糊軟集及其在決策中的應(yīng)用[D].寧波:寧波大學(xué),2012.

[14] 張小紅,裴道武,代建華.模糊數(shù)學(xué)與Rough集理論[M].北京:清華大學(xué)出版社,2013:34-35.

[15] QIN K Y, MENG D, PEI Z, XU Y. Combination of interval set and soft set[J]. International Journal of Computational Intelligence Systems, 2013,6:370-380.

[16] YAO Y Y. Interval set algebra for qualitative knowledge representation[C].Proceedings of the 5th International Conference on Computing and Information, May 27-29,1993,Ontario,Canada,IEEE Computer Society Press,1993:370-375.

[17] MAJI P K, ROY A R. An application of soft sets in a decision making problem[J]. Computers and Mathematics with Applications, 2002,44:1077-1083.

[18] ROY A R, MAJI P K. A fuzzy soft set theoretic approach to decision making problems[J]. Journal of Computational and Applied Mathematics, 2007,203:412-418.

[19] ZOU Y, XIAO Z. Data analysis approaches of soft sets under incomplete information[J]. Knowledge Based Systems,2008,21:941-945.

[20] FENG F, JUN Y B, Liu X Y, Li L F. An adjustable approach to fuzzy soft set based decision making[J]. Journal of Computational and Applied Mathematics, 2010,60:1756-1767.

[21] CAGMAN N, ENGINOGLU S. Soft matrix theory and its decision making[J]. Computers and Mathematics with Applications, 2010,59:3308-3314.

[22] CAGMAN N, ENGINOGLU S. Soft set theory and uni-int decision[J]. European Journal of Operational Research, 2010,207:848-855.

[23] FENG F, Li Y M, CAGMAN N. Generalized uni-int decision making schemes based on choice value soft sets[J]. European Journal of Operational Research,2012,220:162-170.

MultiparameterizedIntervalSoftSet

XU Hong-wei, LIU Wei-feng

(Department of Mathematics and Physics, Zhengzhou Institute of Aeronautical Industry Management, Zhengzhou, Henan 450015, China)

Combined interval soft set with multiparameterized soft set, the new soft set called multiparameterized interval soft set was defined, and multiparameterized soft set and interval soft set were generalized. Then, basic operations and properties of multiparameterized interval soft set were discussed. An application of multiparameterized interval soft set in decision making was given.

soft set; interval soft set; multiparameterized soft set; multiparameterized interval soft set; decision making

2013-07-23.

河南省教育廳科學(xué)技術(shù)研究重點(diǎn)項(xiàng)目(12B110027).

許宏偉(1957-)，男，副教授，江蘇無(wú)錫人，主要從事應(yīng)用數(shù)學(xué)研究.

許宏偉，劉衛(wèi)鋒.多重參數(shù)區(qū)間軟集[J].安徽師范大學(xué)學(xué)報(bào)：自然科學(xué)版，2014，37(4)：320-324.

O159

A

1001-2443(2014)04-0320-05