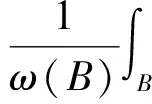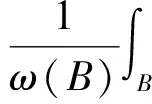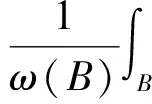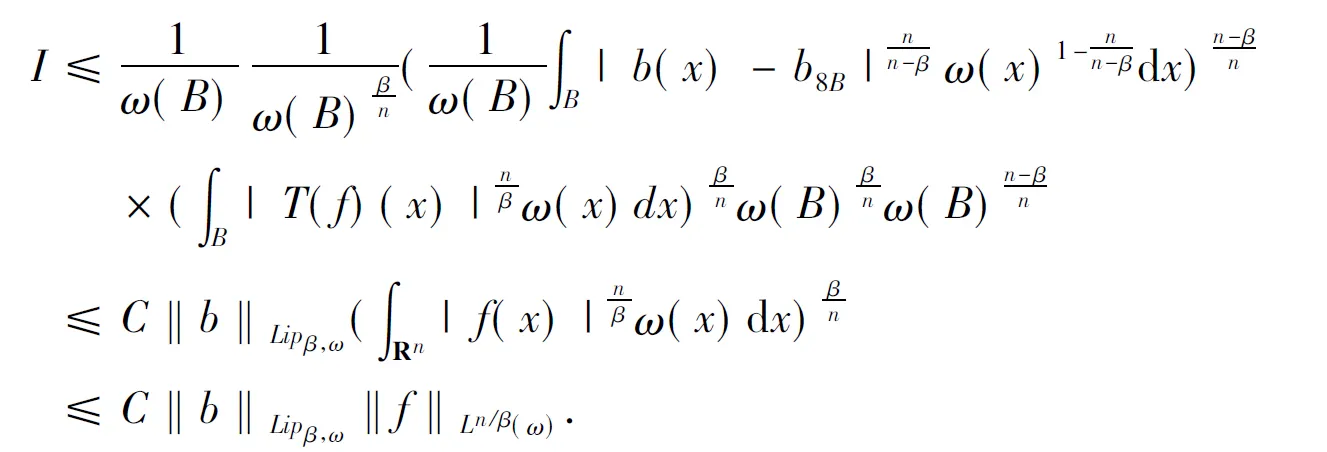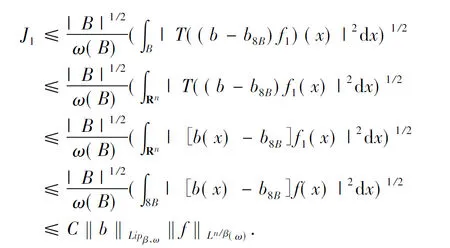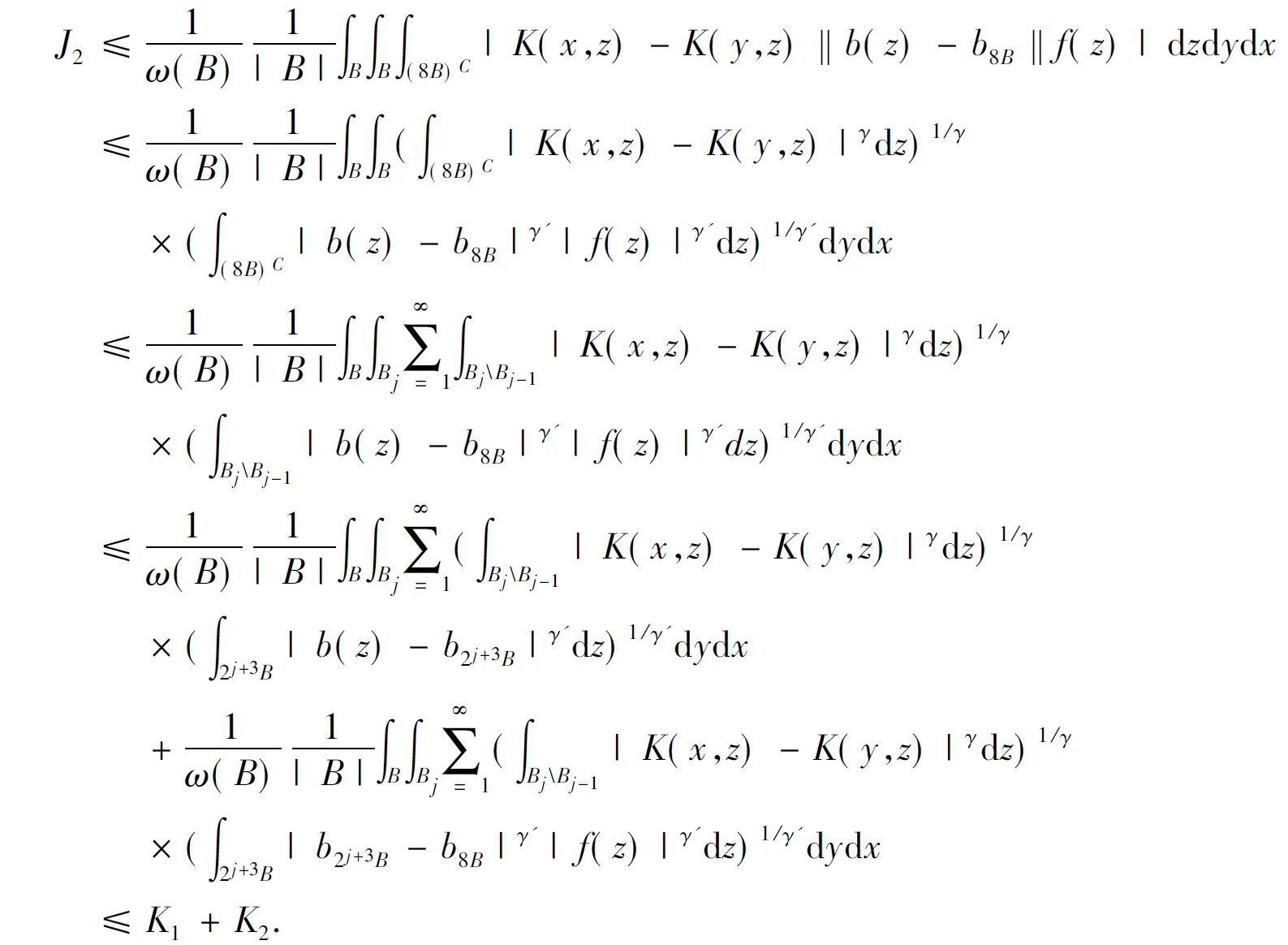廣義Calderón-Zygmund算子與加權(quán)Lipschitz函數(shù)生成交換子的端點(diǎn)有界性
孫 杰
(牡丹江師范學(xué)院 理學(xué)院,黑龍江 牡丹江 157011)
廣義Calderón-Zygmund算子與加權(quán)Lipschitz函數(shù)生成交換子的端點(diǎn)有界性
孫 杰
(牡丹江師范學(xué)院 理學(xué)院,黑龍江 牡丹江 157011)
主要研究了廣義Calderón-Zygmund算子與加權(quán)Lipschitz函數(shù)生成的交換子是從Ln/β(ω)到BMO(ω)有界的.
廣義Calderón-Zygmund算子;加權(quán)Lipschitz空間;加權(quán)BMO空間;交換子;權(quán)函數(shù)
1 引言與結(jié)果
文[1]引入了如下的廣義Calderón-Zygmund算子.
定義1[1]用F(Rn)表示Rn(n≥2)上所有Schwartz函數(shù)構(gòu)成的空間.F′(Rn)是它的對偶空間.設(shè)T:F(Rn)→F′(Rn)是核為K(·,·)的線性算子定義為
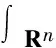
稱算子T是一個廣義Calderón-Zygmund算子,如果它滿足如下性質(zhì):
(1)T是可以延拓為L2(Rn)上的有界算子;
(2)K在除對角線{(x,y)∈Rn:x=y}外光滑且滿足

(1)
這里C>0是不依賴于y和z的常數(shù);
(3)存在一列非負(fù)的常數(shù){μj},使得?j∈N

(2)
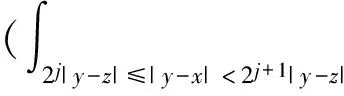
(3)
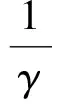
不難看出定義1中的廣義Calderón-Zygmund算子為通常的Calderón-Zygmund算子的推廣[2].文獻(xiàn)[1]和[3]研究了廣義Calderón-Zygmund算子在加權(quán)Lp(Rn)空間以及加權(quán)Hardy空間上的有界性.
把廣義Calderón-Zygmund算子T與函數(shù)b生成的交換子定義為
[b,T]f(x)=b(x)T(f)(x)-T(bf)(x).
2007年,Hu和Gu在文[4]中研究了具有標(biāo)準(zhǔn)核的奇異積分算子與加權(quán)Lipschitz函數(shù)生成的交換子是從Lp(μ)到Lq(μ1-q)有界的.2009年,文[5]研究了當(dāng)1 本文將研究廣義Calderón-Zygmund算子與加權(quán)Lipschitz函數(shù)生成的交換子在端點(diǎn)p=n/β時的加權(quán)有界性.為敘述本文的結(jié)果,首先回憶幾個定義和引理. 定義A∞=∪p≥1Ap.把滿足上面不等式的最小常數(shù)C稱為ω的Ap權(quán)常數(shù),記為[ω]Ap. 定義3[9]設(shè)ω∈A∞,我們稱一個局部可積函數(shù)b(x)屬于加權(quán)BMO(ω)類,如果對于任意球體B,存在常數(shù)C>0,使得 滿足上式最小的C記為‖b‖*ω. 定義4[10]設(shè)ω∈Ap(1≤p<∞),如果存在ε>1和一個固定常數(shù)C>0,對于任意球體B?Rn有 則稱ω滿足反向H?lder不等式,記為ω(x)∈RHε. ‖[b,T]f‖*ω≤C‖b‖Lipβ,ω‖f‖Ln/β(ω). 證明一方面,取λ=fB,有 另一方面, 對λ取下確界,然后對B取上確界,有 引理2[11]設(shè)ω∈A1,則對于球B的任何可測子集E,存在常數(shù)C1,C2>0和0<δ<1,使得 成立.如果ω(x)是常值函數(shù),則δ=1,如果ω(x)不是常值函數(shù),則0<δ<1. 引理3[1]設(shè)T是定義1中的廣義Calderón-Zygmund算子,如果{μj}∈l1,且ω(x)∈A1∩RHγ′,則 由定義4,利用H?lder不等式可得如下引理. 引理4當(dāng)1 定理1的證明由引理1,只須證明對于任何球體B?Rn,總存在常數(shù)λ,使得 其中C>0是與f,b,B,λ,ω?zé)o關(guān)的常數(shù).設(shè)B=B(x0,R)是Rn中任意給定的球體.對于f∈Ln/β(ω),令f1(x)=fχ8B(x),f2(x)=fχ(8B)C(x),,則f(x)=f1(x)+f2(x),于是 =I+J. 對于J,取λ=(T((b-b8B)f2))B, 下面分別估計(jì)J1和J2,對于J1,由于n≥2,0<β<1,有n/β>2,使用H?lder不等式,引理3及引理5,有 下面估計(jì)J2,對于任意的x,y∈B,設(shè)Bj={z∈Rn:|x-z|<2j+1|y-x|},于是BjBj-1={z∈Rn:2j|y-x|≤|x-z|<2j+1|y-x|},應(yīng)用H?lder不等式,有 對于K1,使用式(3)對核進(jìn)行估計(jì),對于1<γ′ 綜上所述定理得證. [1] CHANG D C, LI J F, XIZO J. Weighted scale estimates for Colderón-Zygmund type operator[J]. Contemp Math Amer Math Soc, 2007,445:61-70. [2] STEIN E M. On the functions of littlewood-paley, lusin and marcinkiewicz[M]. Trans Amer Math Soc, 1958,88:430-466. [3] 李俊峰.某些算子及交換子的有界性[D].北京:北京師范大學(xué)數(shù)學(xué)系,2005. [4] HU B, GU J J. Necessary and sufficient conditions for boundedness of some commutators with weighted Lipschitz functions[J]. J Math Anal Appl, 2008, 340(1):598-605. [5] 馬麗娜,江寅生.廣義Calderón-Zygmund算子交換子的有界性[J].高校應(yīng)用數(shù)學(xué)學(xué)報,2009,24(4):453-461. [6] 孫杰.廣義Calderón-Zygmund算子交換子的加權(quán)有界性[J].數(shù)學(xué)的實(shí)踐與認(rèn)識,2012,42(7):205-212. [7] 程民德,鄧東皋,龍瑞麟.實(shí)分析[M].高等教育出版社,2008,357-359. [8] Carcía-Cuerva J. Weighted Hpspaces[J]. Disseration Math, 1979,162:1-63. [9] MUCKENHOUPT B, WHEEDEN R L. Weighted bounded mean oscillition and Hilbert transform[J]. Studia Math, 1976,54(3):221-237. [10] DUOANDIKOETXEA J. Fourier analysis[M]. American Mathematical Society, Providence Rhode lsland, 1995. [11] Journé J L. Calderón-Zygmund operators, Pseudo-differential operators and the Cauchy integral of Calderón. Lecture Notes in Math, 1983,994:1-127. [12] LIN Y, LIU Z G, SONG M M. Lipschitz estimates for commutators of singular integral on weighted herz spaces[J]. Jordan Journal of Mathematics and Statistics(JJMS), 2010,3(1):53-64. WeightedEndpointEstimateforCommutatorofGeneralizedCalderón-ZygmundOperator Sun Jie (College of Science, Mudanjiang Normal University, Mudanjiang 157011, China) In this paper we studied the commutator generated by weighted Lipschitz function and generalized Calderón-Zygmund operator was bounded fromLn/β(ω)to BMO(ω). generalized Calderón-Zygmund operators; weighted Lipschitz space; weighted BMO space; commutator; weighted function 2013-10-14 牡丹江師范學(xué)院省級重點(diǎn)創(chuàng)新預(yù)研項(xiàng)目(SY201325);黑龍江省科技廳科學(xué)技術(shù)研究項(xiàng)目(12531720). 孫杰(1980-),女,黑龍江牡丹江市人,講師,博士在讀,研究方向:調(diào)和分析及小波. 孫杰.廣義Calderón-Zygmund算子與加權(quán)Lipschitz函數(shù)生成交換子的端點(diǎn)有界性[J].安徽師范大學(xué)學(xué)報:自然科學(xué)版,2014,37(4):325-329. O174.2 A 1001-2443(2014)04-0325-05
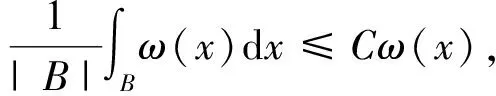

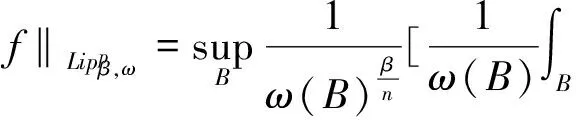
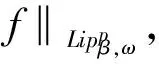
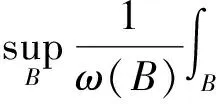

2 預(yù)備知識及引理
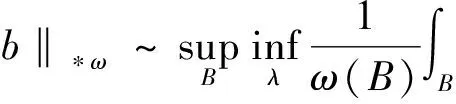






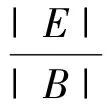






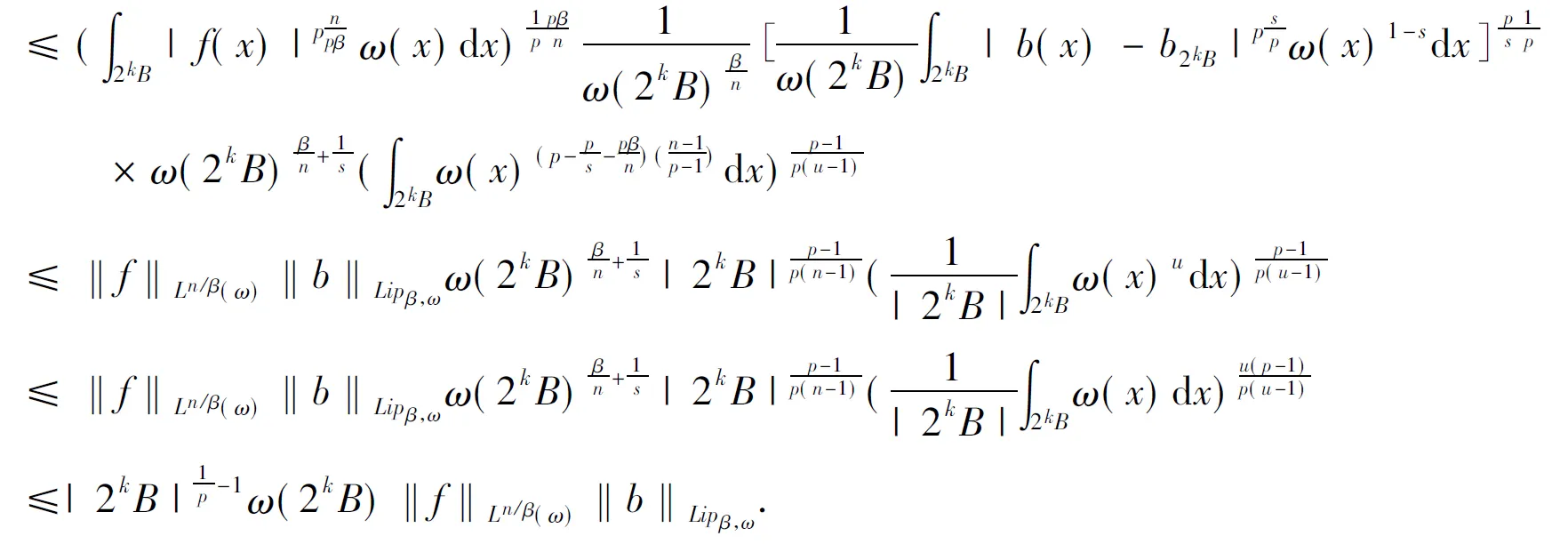
3 定理的證明