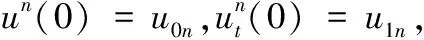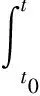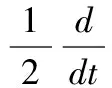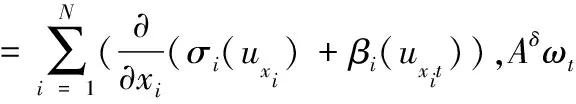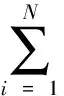一類四階非線性發(fā)展方程整體解的存在唯一性

張媛媛, 王宏偉

(1.開封大學(xué) 數(shù)學(xué)教研部，河南 開封 475000；2.安陽(yáng)師范學(xué)院 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院，河南 安陽(yáng) 455000)

一類四階非線性發(fā)展方程整體解的存在唯一性

張媛媛1, 王宏偉2

(1.開封大學(xué) 數(shù)學(xué)教研部，河南 開封 475000；2.安陽(yáng)師范學(xué)院 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院，河南 安陽(yáng) 455000)

研究一類四階非線性發(fā)展方程整體解的存在唯一性,借助偏微分方程的一些標(biāo)準(zhǔn)技巧對(duì)非線性項(xiàng)進(jìn)行估計(jì),利用嵌入定理和算子半群的方法證明了在相對(duì)較弱的條件下上述問(wèn)題整體解的存在唯一性.

整體解；存在性；唯一性

1 預(yù)備知識(shí)

具耗散項(xiàng)非線性發(fā)展方程的整體解是近年來(lái)偏微分方程研究的熱點(diǎn),目前關(guān)于它的研究主要集中在其存在性和惟一性方面.本文的目的是研究下列一類四階具耗散項(xiàng)方程

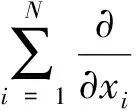
(1)

u|?Ω=0,t>0，

(2)

u(x,0)=u0(x),ut(x,0)=u1(x),x∈Ω.

(3)

(Ω是RN中具有光滑邊界的有界區(qū)域)整體解的存在唯一性.方程(1)有一定的物理模型,它主要描述的是一類具黏彈性材料的振動(dòng)[1-4],此類方程也頻繁出現(xiàn)在具黏彈性構(gòu)形且服從Voight非線性模型的縱向運(yùn)動(dòng)中[5].考慮到偏微分方程和無(wú)窮維動(dòng)力系統(tǒng)的密切關(guān)系,因此筆者嘗試用算子半群的方法探討該問(wèn)題的整體解,最終得到在相對(duì)較弱的條件下整體解的存在性和唯一性.

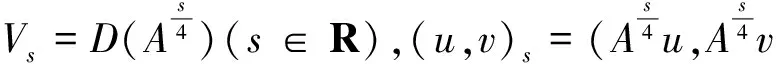
(4)

u(x,0)=u0(x),ut(x,0)=u1(x).

(5)

引理1[6]設(shè)X，Y是Banach空間,并且X?Y.若φ∈L∞(0,T;X)ICw([0,T];Y),則

φ∈Cw([0,T];X).

引理2[7](Aubin-Lions) 設(shè)B0,B和B1是Banach空間,且B0??B?B1,B0,B1是自反的.W={v|v∈Lp0(0,T;B0),vt∈Lp1(0,T;B1)},這里0

引理3[7]設(shè)z(t)非負(fù),是[0,∞)上的絕對(duì)連續(xù)函數(shù),滿足下列不等式

2 主要結(jié)論

定理假定下列條件成立

(ii)βi∈C1(R),βi(s)s≥B3|s|q+2,|βi(s)|≤B4(1+|s|q+1)；

(iii)(u0,u1)∈X2+2δ.

證明:(4)式與ut作內(nèi)積,得:

(6)

(7)

(8)

(8)式積分,并結(jié)合(7)式,得:

≤C(‖(u0,u1)‖X2,T),t∈[0，T].

(9)

設(shè)v=u1+εu，則v滿足

(10)

(10)式與v作內(nèi)積,得:

(11)

(12)

將上式代入(11)式,得:

(13)

通過(guò)計(jì)算,得:

K(u,v)-ερH(u,v)

將上式代入(13)式,得:

(14)

由(12),(14)式并利用引理3,得:

(15)

設(shè)R>0,對(duì)于給定的(u0,u1)∈X2+2δ且‖(u0,u1)‖X2+2δ≤R,則‖(u0,u1)‖X2≤R.

(16)

(17)

(18)

(19)

(20)

(21)

將(19)-(21)式代入(18)式,得:

(22)

(23)

由(4),(22),(23)式和假定,得：

‖utt‖L2(0,T;V2δ-1)≤‖u‖L2(0,T;V1+2δ)+‖ut‖L2(0,T;V1+2δ)+‖u‖L2(0,T;V3+2δ)

≤C(R)(‖u‖L2(0,T;V3+2δ)+‖ut‖L2(0,T;V1+2δ)+1)≤C(R,T), t∈[0,T].

(24)

t>0,j=1,2,…,n，

(25)

顯然,估計(jì)(22)-(23)式對(duì)un仍成立.因此,可從中抽取子序列仍記作un,使得

un→u 在L∞(0,T;V2+2δ) weak*;

(25)式在(0,t)上積分,得到等價(jià)方程

(26)

在(26)式中n→∞,對(duì)t求導(dǎo),可得u是問(wèn)題(4)-(5)的解,且(u,ut)∈L∞(0,T;V2+2δ×V2δ),

ut∈L2(0,T;V2+2δ),utt∈L2(0,T;V2δ-1).

所以,u∈H1(0,T;V2+2δ)?C(0,T;V2+2δ),ut∈H1(0,T;V2δ-1)?Cw(0,T;V2δ-1).

由引理1,ut∈Cw(0,T;V1+2δ).(16)式在(t0,t)上積分,得:

所以,方程在(t0,t)上是可積的.因此,(u,ut)∈C([0,T];V2+2δ×V2δ).

下證(u,ut)連續(xù)依賴X2+2δ上的初值.

設(shè)u,v是問(wèn)題(4)-(5)分別對(duì)應(yīng)于初值u0,u1和v0,v1的兩個(gè)解,則ω=u-v滿足方程

(27)

ω(0)=u0-v0≡ω0, ωt(0)=u1-v1≡ω1.

(27)式與Aδωt作內(nèi)積,由假定(i),(ii),得:

(28)

(29)

(30)

將(29),(30)式代入(28)式,得:

所以,解連續(xù)依賴X2+2δ上的初值,即解的唯一性得證.

[1] ANDREWS G. On the existence of solutions to the equationutt-uxxt=σ(ux)x[J]. Journal of Differential Equations, 1980,35(1):200-231.

[2] KOBAYASHI T, PECHER H, SHIBATA Y. On a global in time existence theorem of smooth solutions to a nonlinear wave equation with viscosity[J]. Mathematische Annalen， 1993,296(1):215-234.

[3] KAVASHIMA S, SHIBATA Y. Global existence and exponential stability of small solutions to nonlinear viscoelasticity[J]. Communications in Mathematical Physics, 1992,148(1):189-208.

[4] 姜禮尚,陳亞浙，等.數(shù)學(xué)物理方程講義.第二版[M].北京：高等教育出版社，38-40.

[5] ANG DD, DINH APN. Strong solutions of quasilinear wave equation with nonlinear damping[J]. SIAM Journal on Mathematical Analysis,1988,19(2):337-347.

[6] NAKAO M. Existence of global smooth solution to the initial boundary value problem for the quasi-linearhyperbolic equation with a degenerate dissipative term[J]. Differ Eqs, 1992,98(1):299-327.

[7] YANG Zhijian. Global attrator for the Kirchhoff type equation with a strong dissipation[J]. Differ Eqs, 2010,249(6):3258-3278.

TheExistenceandUniquenessoftheGlobalSolutionstoaClassofNonlinearEvolutionEquationsofFourth-Order

ZHANG Yuan-yuan1, WANG Hong-wei2

(1.Teaching and Research Department of Mathematics, Kaifeng University,Kaifeng 475000, China; 2.Department of Mathematics and Statistics, Anyang Normal University, Anyang 455000, China)

The existence and uniqueness of the global solutions to a class of nonlinear evolution equations of fourth order were studied. By some standard methods the non-linear terms were estimated. By use of embedding theorem and the method of semigroup,under rather mild conditions the existence and uniqueness of the global solutions for the above-mentioned problem were obtained.

global solutions; existence; uniqueness

2013-09-19

國(guó)家自然科學(xué)基金(10971199)；河南省教育廳科學(xué)技術(shù)研究重點(diǎn)項(xiàng)目(13B110137)；開封市科技發(fā)展計(jì)劃(1401012).

張媛媛(1979-),女,河南省商丘市人,講師,碩士,主要從事偏微分方程與無(wú)窮維動(dòng)力系統(tǒng)的研究.

張媛媛,王宏偉.一類四階非線性發(fā)展方程整體解的存在唯一性[J].安徽師范大學(xué)學(xué)報(bào):自然科學(xué)版,2014，37(4)：330-334.

O175.29

A

1001-2443(2014)04-0330-05