FAHP改進Shapley值法進行工程科技創新收益分配

盛松濤 ，張飛漣 ，張貴金

SHENG Songtao1，2,ZHANG Feilian1,ZHANG Guijin2

1.中南大學 土建學院，長沙 410083

2.長沙理工大學 水利工程學院，長沙 410004

1.Civil Engineering and Architecture Institute,Central South University,Changsha 410083,China

2.Hydraulic Engineering Institute,Changsha University of Science and Technology,Changsha 410004,China

1 引言

隨著科學技術和社會的不斷發展，現代工程項目中新技術出現和更迭的速度越來越快，各個創新主體都會面臨技術資源短缺的問題，而合作創新恰是解決這一問題的重要途徑[1]。工程合作創新是指工程企業之間或企業、研究機構和高等院校之間的聯合創新行為[2]。

創新聯盟成員發揮各自所長，通過創新合作實現“雙贏”或“多贏”的目標，在強調集體收益的基礎上，實現每個成員的收益[3]。然而，如果收益分配不合理，成員企業可能就會產生消極合作，互相推諉甚至猜疑，使創新失去動力，影響創新合作績效。反之，如果收益分配方法使各成員感覺比較公平滿意，則有助于激勵聯盟成員的創新積極性，使合作順利進行，提高創新績效。目前，在實際工程項目中的創新收益分配一般由業主主導，創新成果與收益主要歸業主所有，根據業主的判斷分配部分經濟收益給其他成員；而一旦創新成果達不到預期工程目標，業主的損失又是最大的。這種以業主為主導的分配方法由于本位主義與主觀判斷的局限性，很難科學地體現“多貢獻高收益，高風險高收益”的公平原則。因此，必須圍繞工程技術合作創新的收益分配來設計一套合理的分配機制。

對于創新合作成員間的收益分配，國內外學者已經提出了一些解決方法，主要有Nash合作解法、Shapley法和綜合協商法等。Kuzmin和Emelichev研究了不確定性條件下企業間的有限合作博弈情況，利用企業間具有相關性的線性支付函數研究Nash均衡進行分配的最優性與穩定性[4]。Immorlica，Kleinberg等運用合作博弈理論研究了聯盟最大化收益及其分配問題[5]。Guardiola針對供應鏈聯盟的供應商管理庫存集成策略，應用合作博弈理論，提出將解決多人合作博弈問題的Shapley值法用于解決聯盟利益分配問題[6]。張捍東和生延超等結合風險補償機制和網絡分析法（ANP）改進傳統的Shapley值法去探究不同聯盟的利益分配策略[7-8]。楊晶提出了利益綜合協商法的思想，為不同的利益分配方案確定權重，折中得到一種綜合的利益分配方法，來解決多種協商方案都不一致的問題[9]。從實際應用情況來看，Shapley值法避免了平均分配、吃大鍋飯的現象，調動了合作成員企業的積極性。相對于其他兩種方法容易掌握，可操作性好，應用更為廣泛。但是，該方法未能充分體現聯盟成員在合作中的重要程度與承擔的風險大小，因此，用夏普利值法進行收益分配也有它的不足之處[10]。

2 技術創新聯盟收益分配的Shapley值法

2.1 Shapley值法基本理論

Shapley值是由 Shapley L.S（1953）提出用來解決多成員合作博弈問題的一種數學方法，實質上也是考慮聯盟成員博弈時內部的一種利益分配方案。當多個成員從事某項經濟活動時，對于他們之中若干人組合的每一種合作形式，都會得到一定的收益，當人們之間的利益活動非對抗性時，合作中成員數的增加不會引起效益的減少，這樣全體成員的合作將帶來最大效益，Shapley值法是分配這個最大效益的一種方案，它實現了聯盟總體利益在各成員之間的較公平和有效分配[11]。研究表明，基于Shapley值的科技創新聯盟合作收益分配方法具有穩定性（其解必定惟一且可行），同時完全可以滿足可轉移支付合作博弈解的條件。Shapley值體現的是每個聯盟成員對該聯盟的平均貢獻，反映了個人在集體中的重要性。基于Shapley值的科技創新聯盟合作收益分配方法的最大優點在于其分配原理和分配結果能夠被所有合作方視為公平，分配結果易于被合作各方接受，因此可以將這種方法應用于工程科技創新聯盟合作收益分配問題中。

定義：對給定的n個科技創新成員聯盟合作博弈，設F是定義在 N=(1，2，…，n)上的特征函數，由F決定的一個分配向量由 φ(F)=(φ1(F)，φ2(F)，…，φn(F))，若同時滿足以下公理[11]：

（1）對稱性

設π是 N=(1，2，…，n)的一個排列，即 N到它自身的一一對應，如π是i的對應，πs是 s的對應(s∈N)。若 記 (πF)=F(πs)，?s∈N ，則 對 于 i=1，2，…，n 有φπ1(πF)= φ1(F)。

該公理表示，每個聯盟成員的分配與其被賦予的記號無關，即局中人具有平等關系。

（2）有效性

如果對于所有包含i的子集s都有F(s/i)=Fφ(s)，則

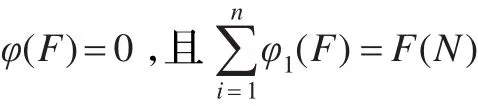
該公理表示，若成員i對于每一個其參加的合作都沒有貢獻，那么就不應該從全體合作的效益中獲得報酬，另外，各成員分配之和應等于全體合作的效益。

（3）可加性

對于定義在i上的任意兩個特征函數u和v：

Φ(u+v)=Φ(u)+Φ(v)

這個公理說明，每個參與聯盟的成員在和博弈中，分配的份額是在兩個分博弈中分配的份額之和。

在以上三條公理的基礎上，Shapley在理論上證明了能夠唯一確定聯盟收益的分配向量，即合作博弈中的一種分配形式，則稱試φ(F)是博弈的Shapley值。科技創新聯盟每個成員獲得的公平收益是合作者參與的所有合作貢獻的加權平均值。其shapley值為：

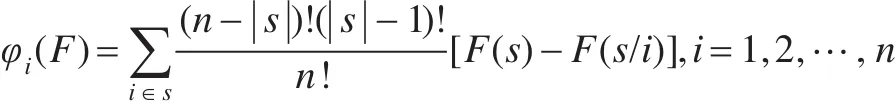
其中|s|為聯盟s中所含參與方的個數；s i表示合作聯盟s中去掉合作方i；F(s)表示s個成員組建的一體化實體的收益值；φi(F)表示第i個成員從合作中獲得的期望分配值。

2.2 實證算例

某水電站的河灣地塊防滲工程，為了快速、經濟、可靠地提高其深厚松軟巖土層的防滲效果，由設計、施工、高校等單位成立了科技創新小組，提出了一種新的帷幕灌漿施工工藝，并在實際灌漿工程中得到了成功的應用。該合作創新項目業主投入科研經費1 000萬元（其中成本560萬元），科研成果節省工程投資1.6億元，取得了多項發明與實用新型專利，并研究得到了系列理論成果，通過創新合作實現了“多贏”的目標。然而，在創新過程中，尤其是項目開始到出成果以后，如何分配創新成果的問題，一度困擾著創新小組，并造成了一些合作不愉快，從而影響創新績效的現象。

現以該工程創新案例為背景，運用Shapley值法來進行創新直接經濟的收益分配。所有的收益都估算成經濟收益，假定設計、施工、高校都可通過人材技術的引進單獨或與另一家單位合作進行此項技術開發，但成本較高。表1是在特定場合單家開發或兩家合作以及三家合作開發情況下的收益情況。

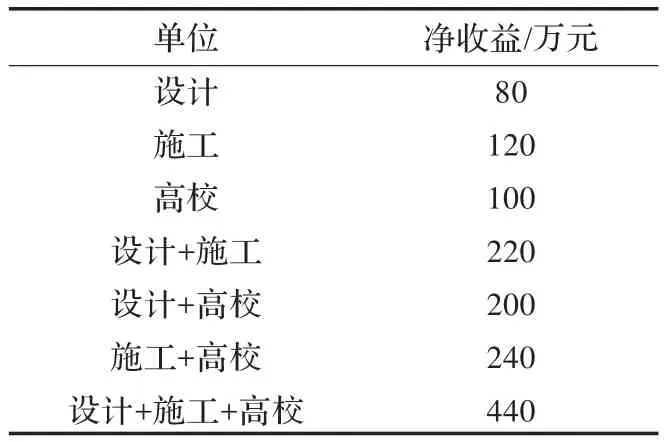
表1 合作各方收益情況表

按夏普利值計算：

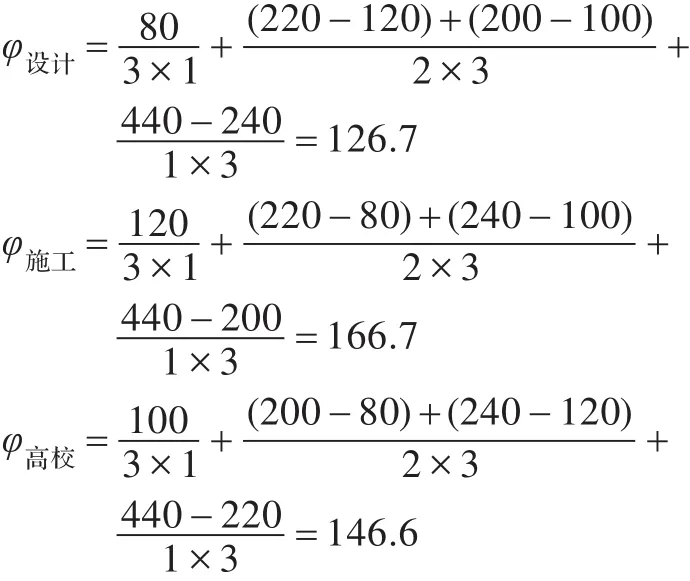
則在夏普利值法下，設計、施工、高校三方各自可以分得126.7萬元，166.7萬元，146.6萬元。可得初步分配比例 φi(v)=（28.80%，37.88%，33.32%）。

2.3 對Shapley值法的評價與改進

用Shapley值法進行產學研合作的收益分配計算較簡單，考慮了多種不同成員與組合的贏利能力，避免了平均分配，聯盟成員獲取的利益不低于非聯盟情況下該成員獲取的利益，合理體現了合作共贏的客觀情況，調動了合作成員企業的積極性。然而進一步分析就會發現Shapley值法也是有缺陷的，它是假設各種聯盟的結合是隨機的，結成聯盟的成員處于平等的地位，這顯然與實際創新聯盟情況不一致。技術創新聯盟一般有一個牽頭單位，各成員的實力與承擔的任務也不盡相同，有的對聯盟貢獻較大，有的對聯盟貢獻相對較小；有的在創新過程中承擔較大的風險，有的成員承擔的創新風險較小。聯盟成員與組合的贏利能力大小與實際貢獻多少并不一定成正比。Shapley值法難以全面體現“多貢獻高收益，高風險高收益”的分配原則。因此，在利益分配機制的設計中就要體現聯盟成員不同的創新貢獻與承擔的創新風險。

本文考慮基于各成員的創新貢獻與承擔的創新風險來對Shapley值法改進，這樣才更符合實際情況。文獻[12]在采用Shapley值法時，對聯盟成員的重要性進行了考慮，通過確定型層次分析法對聯盟成員重要性賦以權重，從而進行了一定的改進；文獻[10]在采用Shapley值法時，對聯盟成員承擔的創新風險進行了考慮，利用各方承擔的風險因子對收益分配進行了修正；文獻[11]采用不確定型層次分析法（AHP）考慮成員對施工投標聯合體的貢獻，改進Shapley值法來進行投標聯合體的利益分配，但其計算比較復雜。為了能夠在很大程度上體現專家判斷的模糊性和不確定性，更好地反映實際狀態，從而使評估結果更具可信性，本文引入FAHP對Shapley值法進行改進，同時考慮創新成員的創新貢獻與風險來分析技術創新聯盟的利益分配機制。

3 基于FAHP法的聯盟成員創新貢獻率改進分配法

在任何領域談到收益分配問題時，首先都要確定收益分配的影響因素。所謂收益分配的影響因素應該是能對收益的產生起貢獻作用的因素，本文認為科技創新合作收益分配問題的主要影響因素包括：角色重要性，合作意識，成本投入，企業實力，承擔風險。其中成本投入包括資金、人力資源、固定資產、技術、時間等方面，都是可證實的具體合作過程中發生的生產性投入，合同中可以依據市場價格明確規定此類成本對應的報酬，這也是科技創新合作進行時，組建合作實體采用股份制的主要原因和依據。除此之外，創新過程中角色的重要性、合作意識、企業實力、承擔風險等很難量化具有相對模糊性。

在利益分配中，實施以貢獻率為基準的分配準則，需要解決的關鍵問題就是如何科學合理地將各成員投入的各種影響收益分配的因素統一量化。本文采用角色重要性、合作意識、成本投入、企業實力、承擔風險作為貢獻率評價指標，然后再對評價指標采用層次分析法進行賦權以定量確定其相對重要性，并采用模糊綜合評價的方法（FAHP）確定各成員綜合貢獻率，并據此來改進Shapley值分配法。

3.1 評價指標權重計算

請相關專家就角色重要性、合作意識、成本投入、企業實力、承擔風險等五個因素的相對重要性進行標度值打分（1～9分制），并構造n=5階判斷矩陣如下[13]：

其中，aij表示第i個指標比第 j個指標的重要程度，aij=1/aji。

據判斷矩陣A計算該層次要素關于相鄰上一層次要素的優先權重，即為計算A最大特征值所對應的特征向量W=(w1，w2，…w5)T，作為該層次 n個要素的優先權重向量。采用求和法計算特征向量：

（1）將矩陣每一列元素正規化（即使列和為1）

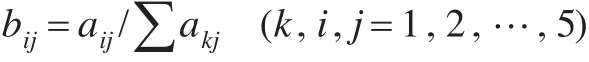
（2）按行求和得權向量：

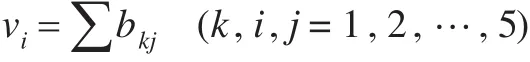
（3）對向量正規化：

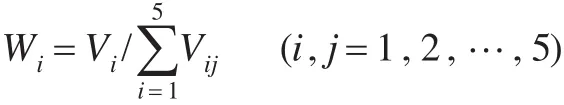
3.2 模糊綜合評價創新成員貢獻率

模糊綜合評價法是根據模糊數學的隸屬度理論把定性評價轉化為定量評價。

首先對評價因素ui={角色重要性、合作意識、成本投入、企業實力、承擔風險}，設評價集V及標準隸屬度集V′，即：V=(v1，v2，…，v5)={無，低，較低，中等，較高，高}，并賦予評價集各元素以量值V′={0，1，3，5，7，9}。

然后構造評判矩陣，由專家結合創新貢獻實際情況進行隸屬度打分。設對第i個評價因素ui進行單因素評價得到一個相對于vj的隸屬度rij，這樣就得到第i個因素的 ui的單因素評判集：ri=(ri1，ri2，…，rin)，因此，m個單因素的評價集就構造出一個總的隸屬度矩陣R：

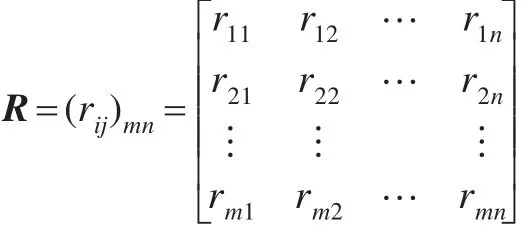
最后對每一個評價因素進行模糊綜合評價即：P=W ×R 。歸一化處理得 P*=(λ1，λ2，…，λn)，即得各創新成員綜合貢獻率λi。

3.3 對Shapley值分配法進行改進

Shapley值利益分配方法假定各成員的投入和承擔的風險相等，但實際情況并不是如此，因此需要運用貢根據貢獻率的利益分擔比例與平均分攤的差值，其中。當?λi≥0時，表示聯盟成員在實際合作中投入的資源和承擔的風險比平均水平高，因此在聯盟利益分配中應該給其正的補償。同理，當?λi≤0時，表示聯盟成員在實際合作中投入的資源和承擔的風險比平均水平低，則應從原先分配取得的利益中扣除部分所得[15]。則考慮創新成員綜合貢獻率λi對Shapley值分配法進行調整，得最終分配值：

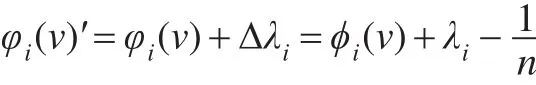
3.4 案例計算與分析

仍然采用第2章防滲帷幕灌漿新工藝科技創新的案例。由科技創新聯盟專家委員會對科技創新中角色重要性、合作意識、成本付出、企業實力、承擔風險等因素進行兩兩比較打分，建立判斷矩陣A。

對矩陣A進行權向量W計算見表2。

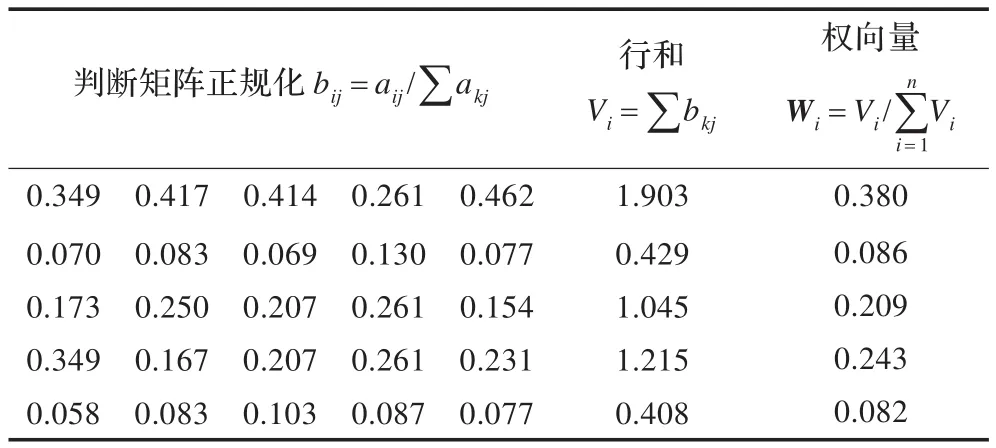
表2 權向量W的計算表

求得W=(0.380 0.086 0.209 0.243 0.082)T，其每一個向量表示創新貢獻因素角色重要性、合作意識、成本付出、企業實力、承擔風險等的相對權重。再由了解本工程實際創新過程的專家針對設計、施工、高校三方的實際貢獻對各因素隸屬度打分得隸屬度矩陣R。

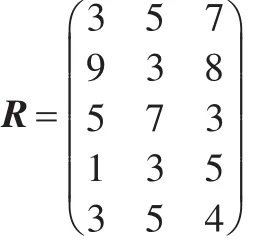
則各創新單位的實際貢獻率矩陣為：

經歸一化處理后得到創新貢獻與風險分配因子P*=（0.25，0.35，0.40），即設計、施工、高校創新貢獻率與風險因子分別為 λ設計=0.25，λ施工=0.35，λ高校=0.40。

運用創新貢獻率與風險因子對Shapley值進行調整，結合前面初步分配比例φi(v)=(28.80%,37.88%,33.32%)，則最終分配比例：

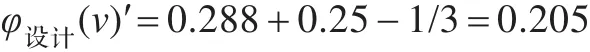
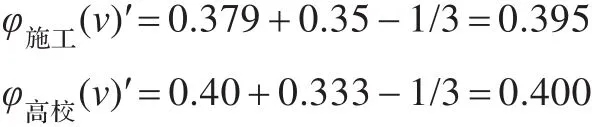
則創新總獲益440萬按創新聯盟貢獻率與承擔風險改進的Shapley值獲益分配分別為：

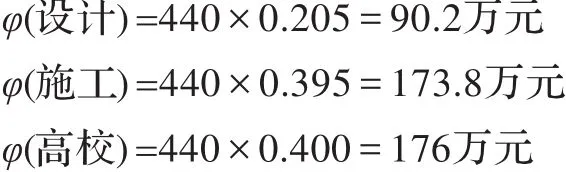
與直接采用Shapley值法分配結果對比，可以發現：設計單位的分配額相對于單純使用Shapley值法分配有所下降，而施工單位和高校有所上升。從該案例的創新實際來看，該項目的核心創新內容與創新風險大的環節都由高校承擔，施工企業將創新成果在施工現場進行驗證實施，設計企業主要提供工程背景資料和相關規范標準。因此改進后的分配方案才是符合客觀實際的。這是因為Shapley值法只是從成員加入聯盟前與加入聯盟后的聯盟收益對比來考慮聯盟內的利益分配，這種純粹以表面數字變化為依據的分配機制存在不足，它忽略了產生這種數字變化的專業背景和創新實際貢獻率，不符合工程技術創新的特點，缺乏足夠的信服力。若按此分配準則，恐很難激勵創新聯盟的積極性，這對三家參與單位而言都是不利的。而利用FAHP基于創新貢獻改進分配方法后，充分肯定了不同成員在聯盟中的價值：首先，相對重要的成員，擔任創新核心任務的高校獲取的利益明顯要高于原分配結果，這是因為其承擔的風險最大且科研實力最強；其次，在聯合體中投入有形資源較多和專業施工能力較強的施工單位分配的利益也略有增加；最后，設計單位分配的利益雖比原來有所下降，但仍比其單獨創新要高，對其顯然是有利的，設計單位仍然會有合作創新的動力。

4 結語

科技創新聯盟中的各成員通過各展所長，相互配合，對創新項目承包實現內部優化組合，可以降低創新成本，提高創新效率和利潤，還可以有效地分散創新風險。但通過聯合創新的收益如何進行合理分配，對于調動各方創新的積極性至關重要。本文從合作博弈的角度，將Shapley值法用于創新聯盟的收益分配研究，并提出包含聯盟成員創新貢獻與風險承擔的評價指標，采用模糊綜合評價法（FAHP）對成員創新貢獻賦以權重從而改進Shapley值法，合理地提高了核心創新單位和承擔風險大的單位的收益分配，分配結果與成員在聯盟中的價值相匹配。希望通過研究合理的利益分配機制，推動更多科研創新企業各取所長組建創新聯盟，增強和提高企業的創新活力和競爭力，為工程技術創新聯盟的穩定發展，獲得更高的創新收益提供理論依據。本方法的不足之處在于計算過程相對較復雜，對于不同的工程項目，隨著創新成員數量和評價指標的增多，計算量將更大，如能將分析過程實現可視化編程，利用計算機進行計算，就能更準確高效地推廣應用本方法。

[1]牛曉霞.基于博弈的校企合作技術創新過程研究[D].西安：西安理工大學，2005：2-4.

[2]傅家驥.技術創新學[M].北京：清華大學出版社，1998：8-10.

[3]宋偉.論科技經濟結合對社會進步的作用[J].科學學研究，1995（4）：35-38.

[4]Emelichev V A，Kuzmin K G.Stability radius of an efficient solution of avector problem of integer linear programming in the G?lder metric[J].Cybernetics and Systems Analysis，2006，42（4）：609-614.

[5]Immorlica N，Kleinberg J，Mahdian M，et al.The role of compatibility in thediffusion of technologies through social networks[C]//Proceedings of the 8th ACM Conference on Electronic Commerce.New York，USA：ACM，2007：75-83.

[6]Guardiola L A，Meca A，Timmer J.Cooperation and profit allocation indistribution chains[J].Decision Support Systems，2007，44（1）：17-27.

[7]張捍東，嚴鐘，方大春.應用ANP的Shapley值法動態聯盟利益分配策略[J].系統工程學報，2009，24（2）：205-210.

[8]生延超.基于改進的Shapley值法的技術聯盟企業利益分配[J].大連理工大學學報：社會科學版，2009，30（2）：34-39.

[9]楊晶，江可申，邸強.基于TOPSIS的動態聯盟利益分配方法[J].系統工程，2008，26（10）：22-25.

[10]鮑新中，劉澄，張建斌.合作博弈理論在產學研合作收益分配中的應用[J].科學管理研究，2008（5）：21-24.

[11]易欣，張飛漣，邱慧，等.不確定AHP和Shapley值應用于投標聯合體利益分配[J].計算機工程與應用，2012，48（27）：194-199.

[12]王鵬，陳向東.基于改進夏普利值的物流企業戰略聯盟利益分配機制研究[J].統計與決策，2011（12）：47-50.

[13]吳恒安.社會評價和水利項目社會評價[J].海河水利，1997（4）：135-137.

[14]郝海，蹤家峰.系統分析與評價方法[M].北京：經濟科學出版社，2007.

[15]蘇秋來.產業技術創新聯盟利益分配研究[D].泉州：華僑大學，2012：40-41.