帶有不完全信息隨機截尾試驗下伽瑪分布尺度參數的點估計

何朝兵, 劉華文

(1.安陽師范學院 數學與統計學院, 河南 安陽 455000; 2.山東大學 數學學院, 濟南 250100)

?

帶有不完全信息隨機截尾試驗下伽瑪分布尺度參數的點估計

何朝兵1*, 劉華文2

(1.安陽師范學院 數學與統計學院, 河南 安陽 455000; 2.山東大學 數學學院, 濟南 250100)

首先通過添加數據得到了帶有不完全信息隨機截尾試驗下伽瑪分布的完全數據似然函數,然后分別利用EM算法和MCMC方法對尺度參數進行了估計,最后進行了隨機模擬試驗,結果表明尺度參數點估計的精度比較高.

完全數據似然函數; EM算法; 滿條件分布; MCMC方法; Gibbs抽樣

伽瑪分布是一類應用廣泛的連續型分布,尤其在水文、氣象、海洋和可靠性領域,并且伽瑪分布與泊松分布、威布爾分布、卡方分布等分布都有著密切的關系.關于伽瑪分布的研究可參看文獻[1-6].近些年來,關于隨機截尾試驗的研究比較多,帶有不完全信息隨機截尾試驗(random censoring test model with incomplete information),簡稱IIRCT,由文獻[7]首次研究,接著文獻[8-18]深入研究了IIRCT下壽命分布的參數估計,但對IIRCT下伽瑪分布的參數估計,卻很少有文獻進行研究.本文通過添加數據得到了IIRCT下伽瑪分布的完全數據似然函數,給出了由EM算法得到的參數的迭代公式,接著利用MCMC方法得到了參數的Gibbs樣本,把Gibbs樣本的均值作為參數的貝葉斯估計,進行了隨機模擬試驗,結果表明參數的EM估計和MCMC估計的精度都較高.

1帶有不完全信息隨機截尾試驗(IIRCT)

設X1,X2,…是獨立同分布的非負隨機變量序列,其分布函數為F(x;θ)=P(Xi≤x),密度函數為f(x;θ),θ是未知參數.又設Y1,Y2,…是獨立的非負隨機變量序列,分布函數分別為G1(y),G2(y),…，密度函數分別為g1(y),g2(y),…且gi(y)與參數θ無關.{Xi}與{Yi}獨立.

為估計參數θ,n個樣品的觀察數據{Zi,1≤i≤n}如下:

1) 當Xi≤Yi時,有兩種情況:Xi以概率ai立即顯示,此時取Zi=Xi;Xi以概率1-ai不被顯示,此時取Zi=Yi.稱ai為失效顯示概率.

2) 當Xi>Yi時,取Zi=Yi.

引入隨機變量αi,βi,i=1,2,…,n.

若Xi≤Yi,αi=1;若Xi>Yi,αi=0.

Xi≤Yi,且未被顯示時,βi=0;其它情況,βi=1.

綜上所述,有

P(βi=1|αi=1)=ai,

P(βi=0|αi=1)=1-ai.

設Zi的觀察值為zi,則基于數據{(zi,αi,βi),1≤i≤n}的似然函數為：

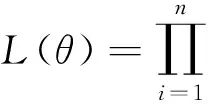
[g(zi)F(zi;θ)(1-ai)]αi(1-βi)·

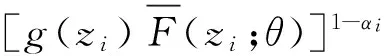
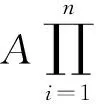
(1)

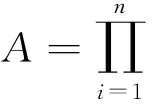
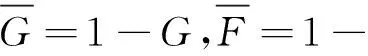
2IIRCT下伽瑪分布參數的點估計

2.1完全數據似然函數

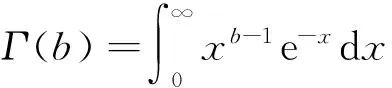
假設IIRCT下產品壽命Xi～Ga(b,θ),且形狀參數b已知,下面對尺度參數θ進行估計.

由(1)式可以看出,伽瑪分布基于截尾數據的似然函數比較復雜,為了方便進行參數估計,下面添加缺損的Xi的值,以獲得完全數據的似然函數.具體如下:

當αi=1,βi=0,即第i個產品失效未被顯示時,添加數據Z1i=Xi=z1i.

在Xi≤zi的條件下,Z1i的條件密度函數為:

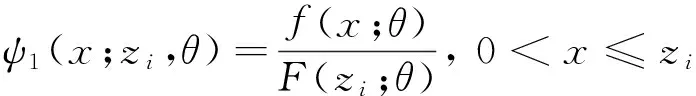
它是區間(0,zi]上的截斷伽瑪分布Ga(b,θ),其樣本可表示為：

z1i=F-1{F(0)+U0[F(zi)-F(0)]}=F-1{U0F(zi)},

其中，F是Ga(b,θ)的分布函數,F-1為其反函數,U0為來自均勻分布U(0,1)的一個隨機樣本.

當αi=0,即Xi>Yi時,添加數據Z2i=Xi=z2i.

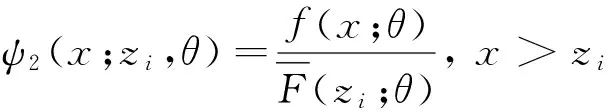
Z2i也服從截斷伽瑪分布,其樣本的獲得與Z1i類似.

令α表示αi組成的向量,β表示βi組成的向量,z表示zi組成的向量,u表示z1i組成的向量,v表示z2i組成的向量,則完全數據似然函數為：

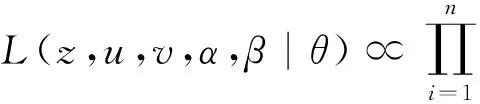
[f(z1i;θ)]αi(1-βi)[f(z2i;θ)]1-αi}=

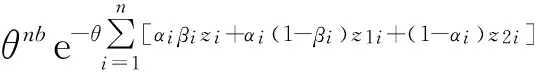
2.2EM算法

EM算法是一種迭代方法,并主要用來求后驗分布的眾數,即極大似然估計,它的每一次迭代由兩步組成:E步(求期望)和M步(極大化).EM算法非常適合處理不完全數據,下面利用EM算法來求θ的MLE.

取θ的先驗分布為伽瑪分布Ga(c,d),c,d已知,即

π(θ)∝θc-1e-dθ,θ>0,c>0,d>0.

則θ的添加后驗分布為：

L(θ|z,u,v,α,β)∝π(θ)L(z,u,v,α,β|θ)∝

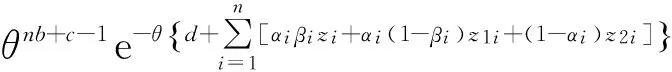
在第m+1次迭代中,假設有估計值θ(m),則可通過E步和M步得到θ的一個新的估計.

令U表示Z1i組成的向量,V表示Z2i組成的向量.

為了書寫方便,簡記(|θ(m)，z，α,β)為(|·).

E步:

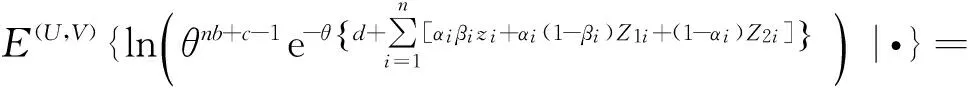
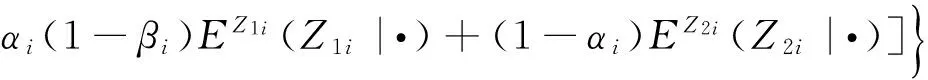
當αi=1,βi=0時,

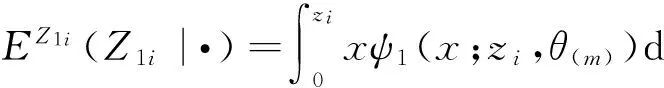
當αi=0時,

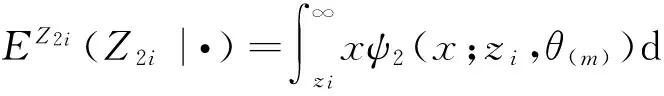
而要獲得Z1i,Z2i期望的顯式表示是不可能的,這時可用Monte Carlo方法完成,這就是所謂的Monte Carlo EM(MCEM)方法,它將E步改為:

(E1) 利用逆變換法隨機產生li個隨機數k1,k2,…,kli.利用逆變換法隨機產生ri個隨機數s1,s2,…,sri;

(E2) 計算

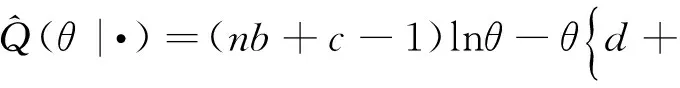
(2)

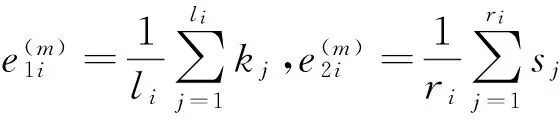
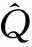
M步:

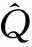
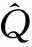
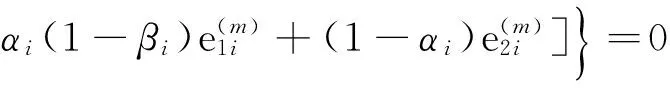
得

θ(m+1)=

(3)

(3)式給出了由EM算法得到的形狀參數θ的迭代公式.

由上述討論可知,EM算法只適用于nb+c-1>0的情況.

2.3參數的貝葉斯估計

當αi=1,βi=0時,

π(z1i|θ,z,z-1i,v,α,β)∝ψ1(z1i;zi,θ),

其中,z-1i={z1j:j≠i}.

當αi=0時,

π(z2i|θ,z,u,z-2i,α,β)∝ψ2(z2i;zi,θ),

其中,z-2i={z2j:j≠i}.

參數θ的滿條件分布為:

π(θ|b,z,u,v,α,β)∝

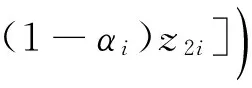
(4)

由于得到了各參數的滿條件分布,下面利用MCMC方法獲得參數θ后驗分布的平穩分布.z1i,z2i的滿條件分布都是截斷伽瑪分布,可以利用逆變換法隨機抽樣;θ的滿條件分布是伽瑪分布,是一個標準分布,所以這3個分布都可以采用Gibbs抽樣.

設θj,j=1,2,…,M1,…,M2為參數θ的一個容量為M2的Gibbs樣本,其中M1為由于不穩定而舍棄的樣本容量,然后利用達到平穩狀態的M2-M1個獨立樣本的均值作為參數θ的貝葉斯估計,即

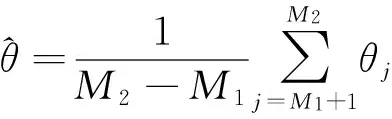
(5)

EM算法得到的估計是后驗分布的眾數(MLE),MCMC方法得到的估計是后驗分布的期望,由于θ的滿條件分布是伽瑪分布,并且滿條件分布抽樣依分布收斂到后驗分布,所以為了討論EM估計和MCMC估計的關系,下面先討論一下伽瑪分布的眾數和期望的關系.

若X～Ga(λ1,λ2),則E(X)=λ1/λ2.當0<λ1≤1時,X的密度函數嚴格下降,眾數不存在;當λ1>1時,X的密度函數是單峰函數,眾數為(λ1-1)/λ2,此時眾數比期望小,但當λ2較大時兩者的差別較小.

3隨機模擬

基于上面的討論,下面進行隨機模擬試驗.設Xi服從伽瑪分布Ga(11,θ),θ=9,取參數θ的先驗分布為伽瑪分布Ga(5.2,0.6);截尾變量Yi～Ga(13,8),失效顯示概率a=0.8,樣本容量分別取n=30,50,100,200,300,500,800,1000.對每一固定樣本量隨機產生一組不完全隨機截尾數據,然后根據此組數據分別利用EM算法和MCMC方法對參數θ進行估計.

運用EM算法時從θ=16開始迭代;運用MCMC方法時,從θ=12.5開始進行Gibbs抽樣,MCMC模擬運行過程中,先進行10000次Gibbs預迭代,以確保參數的收斂性,然后丟棄最初的預迭代,再進行10000次Gibbs迭代,把第10001次至第20000次的迭代值的算術平均值作為λ的估計值. EM估計和MCMC估計的R程序運行結果參見表1.

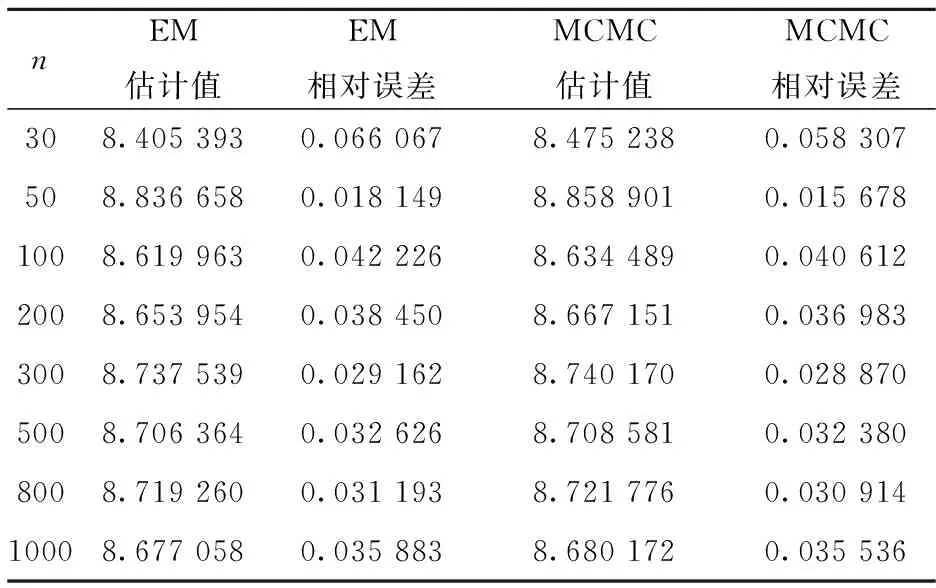
表1 IIRCT下伽瑪分布參數估計的隨機模擬結果Tab.1 Random simulation results of parameter estimation of gamma distribution for IIRCT

當n=300時,EM算法迭代10次,Gibbs迭代20000次,迭代過程參見圖1和圖2.

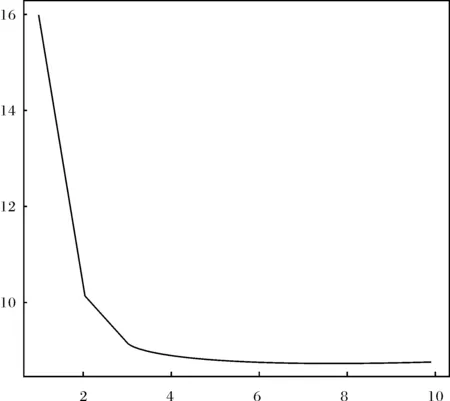
圖1 n=300時,參數θ的EM迭代過程Fig.1 EM iterations of θ with n=300

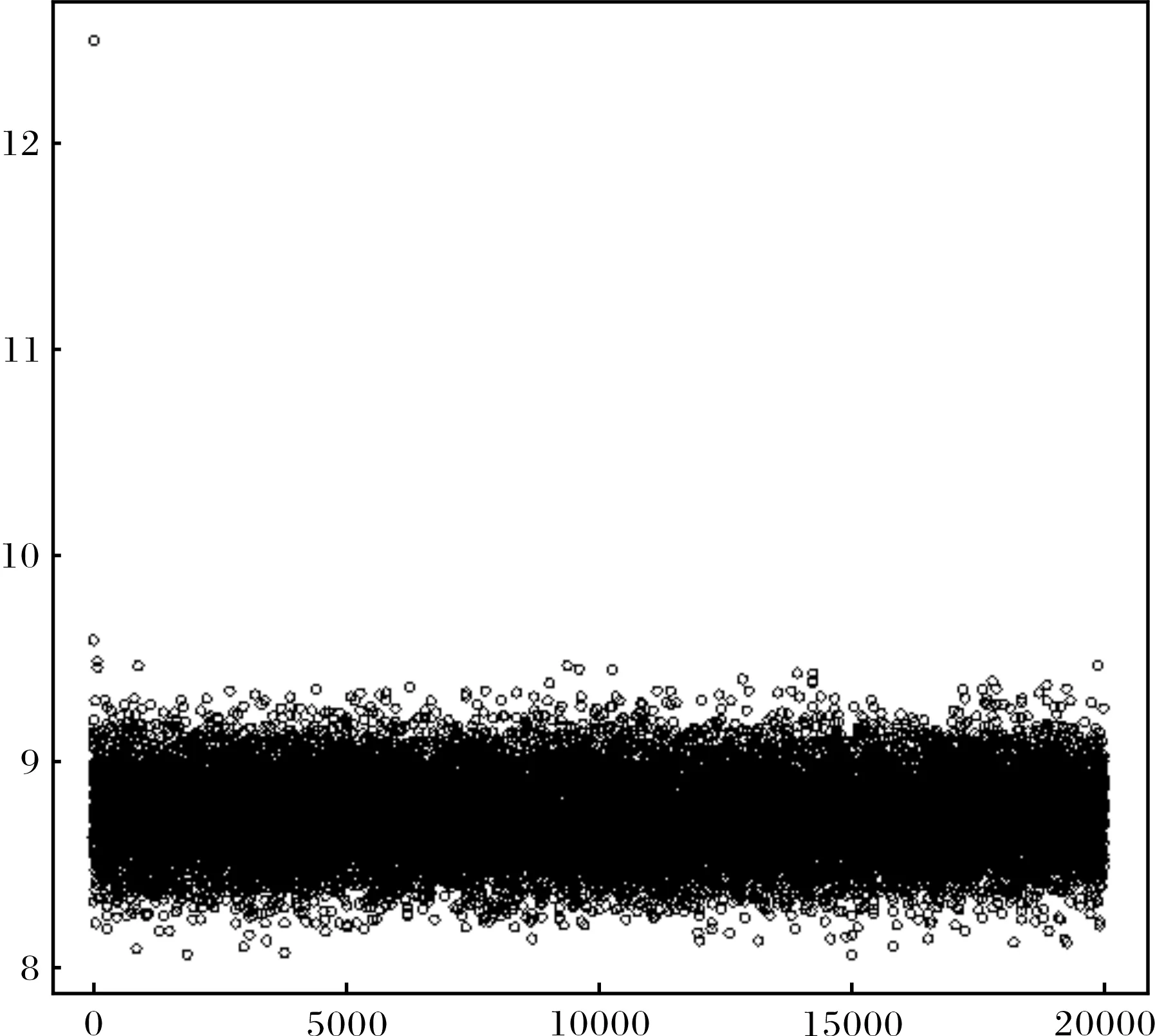
圖2 n=300時,參數θ的Gibbs抽樣迭代過程Fig.2 Gibbs sampling iterations of θ with n=300

由表1可以看出,θ的EM 估計和MCMC估計的差別不大,與真值9的相對誤差都小于7%,MCMC估計比EM估計更接近真實參數θ;樣本量對估計值的影響也不大,說明得到的估計值是比較穩定的,并且精度也較高.

注1 在編寫R程序時用到的函數主要有:

gamma(), unif(), binom(), min(), max(), sum(), mean(), plot()等.

[1] Gupta S S. Order statistics from the gamma distribution[J]. Technometrics, 1960, 2(2): 243-262.

[2] Choi S C, Wette R. Maximum likelihood estimation of the parameters of the gamma distribution and their bias[J]. Technometrics, 1969, 11(4): 683-690.

[3] Wilks D S. Maximum likelihood estimation for the gamma distribution using data containing zeros[J]. Journal of Climate, 1990, 3(12): 1495-1501.

[4] Khodabin M, Ahmadabadi A. Some properties of generalized gamma distribution[J]. J Math Sci, 2010, 4: 9-28.

[5] Huang W, Shu L, Jiang W, et al. Evaluation of run-length distribution for CUSUM charts under gamma distributions[J]. IIE Transactions, 2013, 45(9): 981-994.

[6] Alam A, Rahman M S, Saadat A H M, et al. Gamma distribution and its application of spatially monitoring meteorological drought in barind, bangladesh[J]. Journal of Environmental Science and Natural Resources, 2013, 5(2): 287-293.

[7] Elperin T I, Gertsbakh I B. Estimation in a random censoring model with incomplete information: exponential lifetime distribution[J]. IEEE Transactions on Reliability, 1988, 37(2): 223-229.

[8] Elperin T, Gertsbakh I. Bayes credibility estimation of an exponential parameter for random censoring and incomplete information[J]. IEEE Transactions on Reliability, 1990, 39(2): 204-208.

[9] Ye E. Consistency of MLE of the parameter of exponential lifetime distribution for random censoring model with incomplete information[J]. Applied Mathematics, 1995, 10(4): 379-386.

[10] 陳怡南, 葉爾驊. IIRCT下對數正態和正態分布參數的MLE[J].南京航空航天大學學報:自然科學版, 1996,28(3):376-383.

[11] 陳怡南, 葉爾驊. 帶有不完全信息隨機截尾試驗下Weibull分布參數的MLE[J].數理統計與應用概率, 1996, 11(4):353-363.

[12] 楊紀龍, 葉爾驊. 帶有不完全信息隨機截尾試驗下Weibull分布參數的MLE的相合性及漸近正態性[J].應用概率統計, 2000, 16(1):9-19.

[13] 張曉琴, 張虎明. 帶有不完全信息隨機截尾試驗下Weibull分布參數的MLE的重對數律[J]. 應用概率統計,2002,18(1):101-107.

[14] 宋毅君, 李補喜. 帶有不完全信息隨機截尾試驗下最大似然估計的相合性及漸近正態性[J].應用概率統計, 2003, 19(2):139-149.

[15] 宋毅君, 李補喜, 李濟洪. 帶有不完全信息隨機截尾試驗下最大似然估計的重對數律[J]. 應用概率統計, 2009, 25(2):113-125.

[16] 宋鳳麗, 沈 思. 帶有不完全信息隨機截尾試驗下總體均值型參數的經驗似然[J].應用數學, 2009, 22(1):191-198.

[17] 劉有新, 戴 揚. 帶有不完全信息隨機截尾數據的Fisher信息陣[J].重慶工商大學學報:自然科學版, 2008, 25(6):569-572.

[18] 何朝兵. 帶有不完全信息隨機截尾試驗下幾何分布的參數估計[J].應用數學, 2013, 26(3):574-579.

Point estimation of scale parameter of Gamma distribution for random censoring test model with incomplete information

HE Chaobing1, LIU Huawen2

(1.School of Mathematics and Statistics, Anyang Normal University, Anyang, Henan 455000;2.School of Mathematics, Shandong University, Jinan 250100)

In this paper we firstly obtain the complete data likelihood function of gamma distribution for IIRCT after adding data， then estimate the scale parameter by EM algorithm and MCMC method， respectively. Finally random simulation tests are conducted， and the results show that the point estimations of the scale parameter are fairly accurate．

complete data likelihood function; EM algorithm; full conditional distribution; MCMC method; Gibbs sampling

2014-01-13.

國家自然科學基金項目(61174099); 河南省教育廳自然科學基金項目(2011B110001).

1000-1190(2014)04-0479-04

O213.2; O212.8

A

*E-mail: chaobing5@163.com.