一種Q學習的量子粒子群優化方法

盛歆漪，孫俊，周頔，須文波

1.江南大學數字媒體學院，江蘇無錫 214021

2.江南大學物聯網學院，江蘇無錫 214021

一種Q學習的量子粒子群優化方法

盛歆漪1，孫俊2，周頔1，須文波2

1.江南大學數字媒體學院，江蘇無錫 214021

2.江南大學物聯網學院，江蘇無錫 214021

分析了量子行為粒子群優化算法，著重研究了算法中的收縮擴張參數及其控制方法，針對不同的參數控制策略對算法性能的影響特點，提出將Q學習方法用于算法的參數控制策略，在算法搜索過程中能夠自適應調整選擇參數，提高算法的整體優化性能；并將改進后的Q學習量子粒子群算法與固定參數選擇策略，線性下降參數控制策略和非線性下降參數控制策略方法通過CEC2005 benchmark測試函數進行了比較，對結果進行了分析。

粒子群算法；Q學習；參數選擇；量子行為

粒子群優化算法（Particle Swarm Optimization，PSO）是Kennedy等人受鳥群覓食行為的啟發，提出的一種群體優化算法[1]。自提出以來，PSO算法因其方法簡單、收斂速度快得到了廣泛的應用；但從算法本身來講，PSO并不是一種全局優化算法[2]，許多學者對此提出了許多改進方法，取得了一定的改進效果[3-4]。Sun等人在分析粒子群優化算法的基礎上，深入研究了智能群體進化過程，將量子理論引入了PSO算法，提出了具有全局搜索能力的量子行為粒子群優化算法（Quantum-behaved Particle Swarm Optimization，QPSO）[5-6]。QPSO算法自提出以來，由于計算簡單、編程易于實現、控制參數少等特點，引起了國內外相關領域眾多學者的關注和研究[7-9]，也在一些實際問題中得到了應用[10-13]。針對QPSO算法中的唯一參數（收縮擴張因子），Sun等人使用的是固定參數控制策略，后來Fang提出了隨著進化代數的增加，采用線性減小和非線性減小的參數控制方法，仿真結果表明，在大部分測試函數中都取得了較好的改進效果[14]；Xi等人針對QPSO算法中的粒子貢獻度的差別，提出了權重系數控制算法搜索過程的改進方法，也取得了一定的效果[15]。

在QPSO算法中，算法性能嚴重依賴于收縮擴張因子參數，在進化過程中采用單一的參數控制策略，使粒子缺乏靈活性，這些參數控制方法并不能在進化迭代的每一步中都有效。如果將QPSO算法中的多種參數控制策略同時應用于進化過程中的參數控制，并根據多步進化（向前考察幾步）的效果來選擇其中一種最合適的參數選擇策略作為當前粒子進化的參數，則更有利于算法的整個進化過程。基于這種思想，同時受文獻[16-17]中提到的強化學習啟發，本文提出了一種基于強化學習的量子粒子群優化算法（Reinforcement Learning QPSO，RLQPSO），改善算法的整體性能。

1 量子粒子群優化算法

在粒子群優化算法的群體中，個體（粒子）通過搜索多維問題解空間，在每一輪進化迭代中評價自身的位置信息（適應值）；在整個群體搜索過程中，粒子共享它們“最優”位置信息，然后使用它們的記憶調整它們自己的速度和位置，不斷比較和追隨候選的問題空間解，最終發現最優解或者局部最優解。

基本粒子群算法的進化方程為：

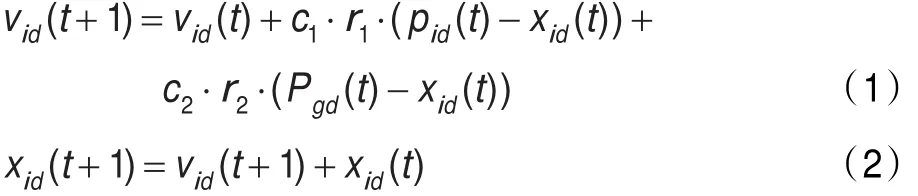
由粒子搜索路徑分析可知，為了保證粒子群算法的收斂性，在粒子搜索過程中，粒子不斷趨近于它們的局部吸引子pi=(pi，1，pi，2，…，pi，n)，方程定義為：

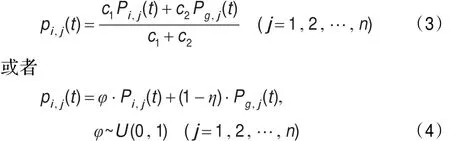
Jun Sun等[5-6]認為在這種搜索機制下，粒子的隨機性就很有限，算法只能描述低智能的動物群體，而不能準確描述思維隨機性很強的人類群體，并且發現人類的智能行為與量子空間中粒子行為極為相似，因此在算法中引入了量子態粒子行為，則對粒子的每一維可以得到概率密度方程Q和分布函數F，方程定義如下：

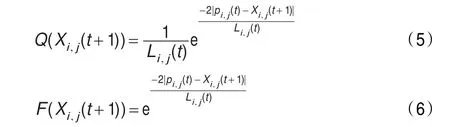
這里，Li，j(t)決定了每個粒子的搜索范圍，使用Monte Carlo方法，可以得到粒子的位置方程：

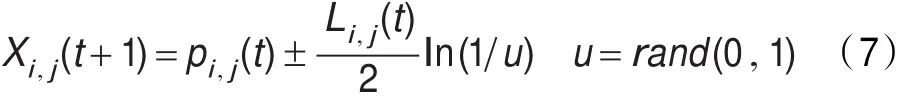
這里u是在（0，1）之間的隨機數。

為了模擬人類群體行為的大眾思維（Main Thoughts），在QPSO算法中引入了最優平均位置值概念，方程定義為：

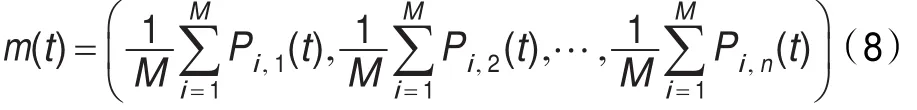
這里M是算法粒子群體的大小，Pi是粒子i的局部最優值，Li，j(t)和粒子的位置量就由以下的方程計算：

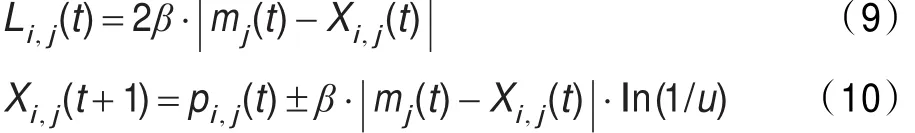
這里，參數β是QPSO算法中的唯一控制參數，稱作擴張收縮系數，調節它可以控制算法的收斂速度。則式（4）（8）（10）組成了具有量子行為粒子群算法的迭代方程組。量子粒子群算法在函數測試[4]、濾波器設計[10]、多階段金融規劃[11]、神經網絡優化[12]和H∞控制[13]等應用中顯示了其優越性。

2 QPSO算法中的參數控制策略

在QPSO算法中，收縮擴張系數β用來調節算法的收斂速度，通過大量的仿真測試，β≤1.781時能夠保證算法收斂[8]，在基本QPSO中，通過仿真測試，固定取值策略條件中，β=0.8在大多數的測試函數條件下能夠取得較好的測試結果。

為了改善QPSO算法的性能，方偉[14]提出了線性遞減的參數調整策略和非線性遞減的參數調整策略，即

（1）線性遞減策略

文獻[14]中的大量仿真測試表明，對于不同的測試函數，以上參數控制策略（包括固定值參數）各有優勢，各自能夠在不同的問題中取得優于其他參數控制策略的仿真結果。那么，對于一個未知問題，如何選擇參數的控制策略才能取得更好的尋優結果，因此，受強化學習思路的啟發，將參數不同的選擇策略視為行動（action），在群體粒子進化過程的每一個迭代步，選擇一個合適的行動（參數）來控制粒子的搜索過程。并且，在作出行動決策之前，對行動的選擇多向前考慮幾步，則參數最終選擇結果正確的概率更高，更能提高算法的整體性能。因此，在粒子選擇行動時，可以通過粒子多步進化的效果評價各種行動（參數選擇策略）的優劣。

3 Q學習的量子粒子群優化算法（QLQPSO）

3.1 Q學習方法

Q學習是一種與問題模型無關的增強學習方法，通過選擇最大化代理帶折扣的累積收益的行動，學習到代理的最優行動策略。在QPSO算法中，若把個體進化過程中的參數選擇策略看成行動，這樣個體選擇最優參數策略就轉化為代理選擇最優行動。

假設代理的狀態設為s，行動設為a；則代理在任何狀態下可選擇的行動集合均為A={a1，a2，…，an}，即代理在每個狀態都有n個可供選擇的行動。則代理的最大折扣回報基本形式為：

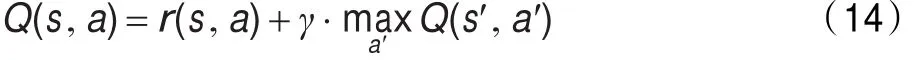
其中r(s，a)為代理在狀態s下選擇行動a后的立即收益；a′為代理在下一個狀態s′情況下可選擇的行動；表示代理在下一個狀態s′選擇不同行動所能得到的最大回報值；γ(0≤γ＜1)為折扣因子，γ決定滯后收益對最優行動策略選擇的影響。根據式（14），如果向前看m+1步，個體開始選擇的參數策略為a，那么在忽略狀態變量的情況下，代理選擇行動a時的收益為：

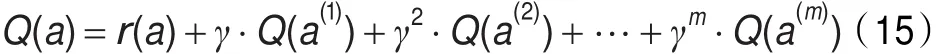
其中，m表示向前看的步數；a，a(i)∈A，且1≤i≤m。由式（15）可知，當γ=0，Q值的計算值降為只向前看一步，γ接近于1時，滯后收益對最后參數選擇策略的影響將變得越來越大。

3.2 QLQPSO算法原理

根據Q學習方法，在QPSO算法中將群體中的粒子看作代理，擴張收縮系數β的選擇策略看作代理行動的集合，則可以實現量子粒子群優化算法和Q學習方法之間的映射。定義fp(a)為群體中父代個體對應的適應度函數值，fo(a)為采用參數選擇策略a后個體對應的適應度函數值，那么個體的立即收益可以定義為r(a)= fp(a)-fo(a)。如果本例中粒子可選行動（參數選擇策略）個數為n，粒子一次進化后共產生n個后代，每個后代采用n個策略進化，二次進化后的后代個數為n2，同理m次進化后，產生的后代共有nm個，要確定一次參數選擇策略，需要進行指數級運算，計算量非常巨大，不適用。為此將問題簡化，粒子第一次進化后產生n個新粒子；該n粒子再次進化，每個個體又產生n個新粒子，通過計算每個個體產生的新粒子的立即收益，采用Boltzmann分布計算這組再次生成的新粒子被保留下來的概率。

根據計算出的概率，選擇其中一個新個體保留下來，被保留的后代再采用同樣的方式產生n個后代，并保留其中的一個后代。通過這種簡化后，則m次進化后，一個粒子累計產生的個體數為n+(m-1)·n2，用于計算Q值需要保留的個體數為m×n，那么問題時間復雜度降為多項式級。

將立即收益帶入式（15），并化簡后可得：

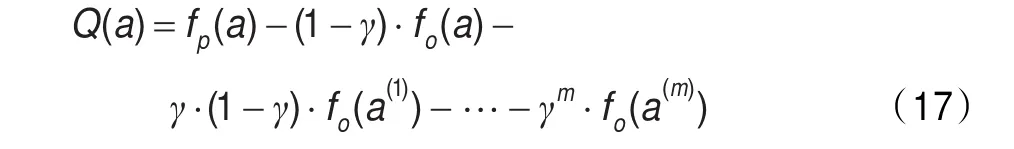
QLQPSO算法設計如下：

（1）初始化參數設置：包括群體個數；擴張收縮系數β取值范圍；算法迭代次數；折扣因子γ。計算Q值所需向前看的步數m；隨機產生的初始解x(i)，并設置pbest(i)=x(i)，并計算全局最優值gbest。

（2）根據式（5）計算局部吸引子p(i)。（3）根據式（8）計算平均最優值mbest。（4）根據QPSO算法迭代方程（9）（10）更新各個粒子的新位置。

（5）按照Q學習方法選擇最優參數策略β：

①對于每個新粒子，使用給定的n個參數選擇策略產生n個新的后代粒子，并設定t=1；

②Do Whilet＜m

每個后代使用式（9）產生n個新后代，根據式（16）選擇其中一個保留，令t++；

③計算每個參數選擇策略對應的Q值，選擇使Q最大化的參數選擇策略所對應的β值為當前β值，同時舍棄其他n-1個β值。

（6）每個粒子按照式（8）～（10）更新位置值，并生成新的群體。

（7)回到（4）直至循環條件結束。

3.3 QLQPSO算法分析

張化祥等人[17]對基于Q學習的適應性進化規劃算法（QEP）的收斂性進行了證明，QLQPSO算法收斂性的證明過程與此類似，本文在此不再對其收斂性進行證明。根據Q學習方法的原理，可以知道在QLQPSO算法執行初期，在Boltzmann分布中，溫度T處于較大值，粒子在參數選擇進化策略空間進行探索；隨著進化步數的增加，T越來越小，粒子探索的成分逐步減小，越來越趨向于選擇適應度函數值大的參數進化策略（本例中為最小化問題，因此為最優化函數值小），此時粒子選擇最優參數策略的概率逐步增加。

4 QLQPSO算法仿真分析

4.1 仿真設置

為了測試和比較Q學習的QPSO算法性能，本文和固定系數QPSO（BQPSO）算法、系數線性下降的QPSO算法（LDQPSO）、系數開口向上的非線性遞減QPSO算法（UPQPSO）和系數開口向下的非線性遞減QPSO算法（DNQPSO）進行了測試比較，測試函數使用CEC2005 benchmark測試函數[18]，其中F1到F6為單峰函數，F7到F12為多峰函數。優化問題分別設置為：BQPSO算法的β值為0.8，LDQPSO算法、UPQPSO算法、DNQPSO算法的β從1.0下降到0.5，QLQPSO算法的參數選擇行動策略為上述四種算法的參數選擇方法，滯后因子γ為0.5，T的初始溫度為100℃。問題維數為30，算法對應的最大迭代次數為5 000，粒子數為40；每個問題的求解都應用算法隨機獨立運行50次。

4.2 仿真結果與討論

表1給出了五種算法對各測試函數在不同粒子數、不同維數及不同迭代次數的情況下得到的50次仿真結果的目標函數值的平均值和標準方差。圖1中給出了不同算法在40個粒子30維的情況下50次仿真的平均收斂曲線。從表1中各種算法的仿真結果看，QLQPSO在12個測試函數中，9個取得了最好的結果，LDQPSO、UPQPSO、DNQPSO各取得了一次最優值。在QLQPSO取得的8次最優的情況下，對于Shifted Schwefel’s Problem 1.2函數（F2）、Shifted Rotated High Conditioned Elliptic函數（F3）、Shifted Schwefel’s Problem 1.2 with Noise in Fitness（F4）、Shifted Rastrigin’s函數（F9）、Shifted Rotated Weierstrass函數（F11），QLQPSO取得了明顯的優勢。另外從圖1的收斂曲線可以得知，對于Shifted Sphere函數（F1）、Shifted Rotated Griewank’s Function without Bounds函數（F7）和Shifted Rotated Ackley’s函數（F8），QLQPSO算法取得了最優值，雖然結果和其他算法比較接近，但算法表現出初期的收斂速度遠高于其他算法；對于Schwefel’s Problem 2.6 with Global Optimum on the Bounds函數（F5）、Shifted Rosenbrock函數（F6）、Shifted Rotated Rastrigin’s（F10）和Schewefel’s Problem 2.13函數（F12），LDQPSO算法和UPQPSO分別取得了最優值，但是QLQPSO的結果和它們很接近，但是在初期（1 000次迭代）的收斂速度是最快的。以上說明，提出的Q學習QPSO算法大大提高了算法的收斂速度，并且在大多數測試函數中表現了優異的性能。

5 結束語

分析了QPSO算法的進化方程，并研究了算法中的控制參數選擇方式對參數性能的影響，不同的參數選擇方式針對不同電費優化問題有各自的優化特點，這對控制參數選擇提出了更高的要求。針對算法參數選擇上的限制，提出了引入Q學習的思想來根據優化問題自適應調整參數的選擇，并給出了改進后的算法執行過程。最后應用CEC2005測試函數對改進后的算法和其他幾種不同的控制參數選擇策略進行了仿真比較，仿真結果顯示改進后的算法在大部分測試函數上能夠取得更優的結果，其他函數也能夠取得和其他方法相近的結果，因此改進后的算法能夠提高QPSO算法的整體性能。

表1 不同算法運行50輪后的平均最優值及方差

圖1 五種算法優化不同標準測試函數的目標函數值的收斂曲線比較

[1]Kennedy J，Eberhart R.Particle Swarm Optimization[C]// Proceedings of IEEE International Conference on Neural Network，1995：1942-1948.

[2]van den Bergh F.An analysis of Particle Swarm Optimizers[D].University of Pretoria，2001.

[3]Zheng Yongling，Ma Longhua，Zhang Liyan.Empirical study of particle swarm optimizer with an increasing inertiaweight[C]//Proceedings of IEEE Congress on Evolutionary Computation 2003（CEC 2003），Canbella，Australia，2003：221-226.

[4]Clerc M.Discrete Particle Swarm Optimization[M]//New Optimization Techniques in Engineering.[S.l.]：Springer-Verlag，2004.

[5]Sun J，Feng B，Xu W.Particle Swarm Optimization with particles having quantum behavior[C]//IEEE Proc of Congress on Evolutionary Computation，2004：325-331.

[6]Sun J，Xu W，Feng B.A global search strategy of quantum-behaved Particle Swarm Optimization[C]//Cybernetics and Intelligent Systems，Proceedings of the 2004 IEEE Conference，2004：111-116.

[7]Sun J，Wu X，Palade V，et al.Convergence analysis and improvements of quantum-behaved particle swarm optimization[J].Information Sciences，2012，193：81-103.

[8]Sun J，Fang W，Wu X，et al.Quantum-behaved particle swarm optimization analysis of individual particle behavior and parameter selection[J].Evolutionary Computation，2012，20（3）.

[9]Omranpour H，Ebadzadeh M，Shiry S，et al.Dynamic Particle Swarm Optimization for multimodal function[J].International Journal of Artificial Intelligence，2012，1（1）：1-10.

[10]Chen W，Sun J，Ding Y R.Clustering of gene expression data with Quantum-behaved Particle Swarm Optimization[C]//IEA/AIE.Zurich：Springer-Verlag，2008：388-396.

[11]Chai Zhilei，Sun Jun，Cai Rui，et al.Implementing Quantum-behaved Particle Swarm Optimization algorithm in FPGA for embedded real-time applications[C]//2009 Fourth International Conference on Computer Sciences and Convergence Information Technology，2009：886-890.

[12]Omkar S N，Khandelwal R，Ananth T V S，et al.Quantum behaved Particle Swarm Optimization（QPSO）for multi-objective design optimization of composite structures[J].Expert Systems with Applications，2009，36（8）：11312-11322.

[13]Goh C K，Tan K C，Liu D S，et al.A competitive and cooperative co-evolutionary approach to multi-objective particle swarm optimization algorithm design[J].European Journal of Operational Research，2010，202：42-54.

[14]Fang W.Swarm intelligence and its application in the optimal design of digital filters[D].2008.

[15]Xi M，Sun J，Xu W.An improved quantum-behaved particle swarm optimization algorithm with weighted mean best position[J].Applied Mathematics and Computation，2008，205（2）.

[16]Sutton R S，Barto A G.Reinforcement learning：an introduction[M].Cambridge：MIT Press，1998.

[17]張化祥，陸晶.基于Q學習的適應性進化規劃算法[J].自動化學報，2008，34（7）：819-822.

[18]Suganthan P，Hansen N，Liang J J，et al.Problem definitions and evaluation criteria for the CEC 2005 special session on real-parameter optimization[R].Singapore：Nanyang Technological University，2005.

SHENG Xinyi1,SUN Jun2,ZHOU Di1,XU Wenbo2

1.School of Digital Media,Jiangnan University,Wuxi,Jiangsu 214021,China
2.School of Internet of Things,Jiangnan University,Wuxi,Jiangsu 214021,China

Quantum-behaved Particle Swarm Optimization algorithm is analyzed;contraction-expansion coefficient and its control method are studied.To the different performance characteristics with different coefficients control strategies,a control method of coefficient with Q-learning is proposed.The proposed method can tune the coefficient adaptively and the whole optimization performance is increased.The comparison and analysis of results with the proposed method,constant coefficient control method,linear decreased coefficient control method and non-linear decreased coefficient control method based on CEC2005 benchmark function is given.

Particle Swarm Optimization（PSO）algorithm;Q-learning;parameter selection;quantum behavior

A

TP301

10.3778/j.issn.1002-8331.1402-0206

SHENG Xinyi,SUN Jun,ZHOU Di,et al.Quantum-behaved particle swarm optimization method based on Q-learning. Computer Engineering and Applications,2014,50（21）：8-13.

國家自然科學基金（No.61170119，No.60973094）；江蘇省自然科學基金（No.BK20130160）。

盛歆漪（1975—），女，博士研究生，講師，主要研究方向：智能控制，優化算法，交互設計；孫俊（1973—），男，博士，副教授，主要研究方向：優化算法，機器學習；周頔（1983—），女，博士，副教授，主要研究方向：優化算法，圖像識別；須文波（1944—），男，教授，博導，主要研究方向：智能控制，先進算法。E-mail：sheng-xy@163.com

2014-02-20

2014-05-04

1002-8331（2014）21-0008-06

CNKI出版日期：2014-05-22，http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1402-0206.html