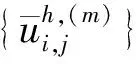一類橢圓邊值問題緊有限差分方法的單調迭代算法
武文佳
(上海電機學院 數理教學部, 上海 201306)
一類橢圓邊值問題緊有限差分方法的單調迭代算法
武文佳
(上海電機學院 數理教學部, 上海 201306)
對一類二維常系數半線性橢圓邊值問題的四階緊有限差分方法,建立了有效的單調迭代算法,給出相應的收斂性分析,并通過數值實驗驗證了理論分析的正確性。
半線性橢圓邊值問題; 單調迭代算法; 收斂率
橢圓型偏微分方程的邊值問題被廣泛應用于物理、生物、工程等很多應用領域,對此類問題建立緊有限差分方法,并給出有效的單調迭代算法有著重要的理論意義和實際的應用價值[1-2]。近年來,對此類邊值問題的四階緊有限差分方法得到了廣泛的關注和應用[3-10]。在以往的研究中,已經對一類常系數二維半線性橢圓邊值問題建立了四階緊有限差分格式[11]。由于問題本身的非線性,得到的有限差分方程組為線性代數方程組;對此類方程組,一個基本的問題就是建立有效的單調迭代算法。本文主要對文獻[11]中的緊有限差分格式建立有效的單調迭代算法,并給出數值實驗結果。
1 緊有限差分格式
本文研究如下的二維半線性橢圓邊值問題:
(1)
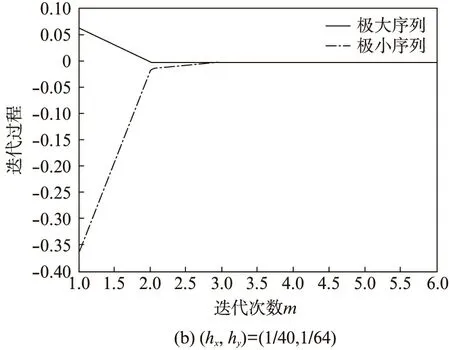
式中,Ω?R2為矩形區域的組合,其邊界平行于x軸或y軸;函數f(x,y,u)和φ(x,y)在定義域內充分光滑;函數f(·,·,u)關于u為非線性的、函數c(x,y)和d(x,y)為Ω上正的光滑函數。

引入中心差分算子替換方程中的微分算子,通過緊逼近截斷誤差項,文獻[11]中已經建立了如下的四階緊有限差分格式:
(2)
它等價于
(3)
式中:

其中,αi,j、βi,j、Ci,j、Di,j、γi,j分別為系數,即:
ci,j=c(xi,yj),di,j=d(xi,yj)
且
(4)
式中,σ=hx/hy為步長比。
由式(4)可知,存在正的常數h*,使得對于所有的hx (5) (6) 同樣,由式(4)可知,給定任意非負常數M,存在正常數h(M),使得所有的hx (7) (8) 引理1假設式(6)成立,M為非負常數。若hx (9) 證明根據式(9),結合文獻[12]206頁中的定理1,顯然可證引理的結論成立。 (10) (11) 證明根據式(10)、(11),結合定義2,類似引理1的證明過程,可證引理2結論成立。 (12) 用這些常數作為參數,本文給出如下Picard型線性單調迭代算法: (13) 本文將證明式(13)具有單調收斂性。 (14) 證明證明過程與文獻[11]中定理2的證明過程類似(只需將文獻[11]中引理1用本文引理2替代),此處略。 定理1給出了式(13)的單調收斂性,但是,顯示收斂率還是未知的,以下給出保證序列幾何收斂的充要條件。 (15) 定理2設定理1的條件和式(15)成立,且hx (16) 且 (17) 根據式(15),有 (18) (19) 根據引理2可知(A-BM*)-1存在且非負,這說明向量Y=(A-BM*)-1E為正,其中,E為所有元素都是1的向量。令Yi為Y的第i個分量,定義D=diag(1/Yi),其中,1/Yi即為導出定理中的Xi,則有 D(A-BM*)D-1E=D(A-BM*)Y=DE>0 或 D(A+BM)D-1E>DB(M+M*)D-1E 由引理2可知(A+BM)-1非負,故有 D(A+BM)-1B(M+M*)D-1E 再根據M*≥-M可得 因此,由式(19)可知 這就證明了對于極大序列,式(16)成立。同理可證,對于極小序列,式(16)也成立。 式(16)表明,由式(13)得到的極大和極小序列至少為幾何收斂的,收斂率ρ*由式(17)給出。 現將上述單調迭代算法應用于實際應用中的模型問題,來說明四階緊有限差分方法的精度和本文提出的單調迭代算法的有效性。 考慮如下人口增長模型中常見的問題: (20) 式中,Ω=(0,1)×(0,1);k為正常數;函數ζ(x,y)和φ(x,y)為已知的,使得 u(x,y)=sin(4πx)sin(πy) 為模型問題式(20)的精確解。 選取k=1.5,用本文提出的單調迭代算法式(13)計算緊有限差分方程組,其中迭代終止的準則為 圖1 極大序列和極小序列在點(0.5,0.5)處的單調收斂性Fig.1 Monotone convergence of maximal andminimal sequences at (0.5,0.5) 為說明數值解的四階精度,選擇hx=hy=h。表1給出了取不同h時數值解的L∞-誤差errorL∞(h)和階數orderL∞(h),其中ε=10-13。L∞-誤差和階數計算如下: 其中,u表示原問題的精確解。 計算結果如表1所示。由數值結果可知,數值解具有四階精度,這與理論分析相吻合,同時說明了本文提出的單調迭代算法的有效性。 表1 數值解的L∞-誤差和階數Tab.1 L∞-error and order of computed solution [1] Banks H T.Modeling and control in the biomedical sciences[M].Berlin,Heidelberg,New York: Springer-Verlag,1975: 45-49. [2] ?zisik M N.Boundary Value Problems of Heat Conduction[M].New York: Dover Publications,1989: 20-24. [3] Berikelashvili G,Gupta M M,Mirianashvili M.Convergence of fourth order compact difference schemes for three-dimensional convection-diffusion equations[J].SIAM Journal on Numerical Analysis,2007,45(1): 443-455. [4] Gopaul A,Bhuruth M.Analysis of a fourth-order scheme for a three-dimensional convection-diffusion model problem.SIAM Journal on Scientific Computing,2006,28(6): 2075-2094. [5] Wang Xuan,Yang Zhifeng,Huang Gordon,et al.A high-order compact difference scheme for 2D Laplace and Poisson equations in non-uniform grid systems[J].Communications in Nonlinear Science and Numerical Simulation,2009,14(2): 379-398. [6] Wang Jie,Zhong Weijun,Zhang Jun.A general meshsize fourth-order compact difference discretization scheme for 3D Poisson equation[J].Applied Mathematics and Computation,2006,183: 804-812. [7] Asthana K,Sengupta T K.An explicit higher order difference scheme on a compact stencil for elliptic equations on curvilinear geometries[J].Applied Mathematics and Computation,2014,242: 143-158. [8] Hejranfar K,Ezzatneshan E.Implementation of a high-order compact finite difference lattice Boltzmann method in generalized curvilinear coordinates[J].Journal of Computational Physics,2014,267: 28-49. [9] Han Fei,Dai Weizhong.New higher-order compact finite difference schemes for 1D heat conduction equations[J].Applied Mathematical Modelling,2013,37(16-17): 7940-7952. [10] Zhai Shuying,Feng Xinlong, He Yinnian.A new method to deduce high-order compact difference schemes for two-dimensional Poisson equation[J].Applied Mathematics and Computation,2014,230: 9-26. [11] 武文佳.一類二維半線性橢圓邊值問題的四階緊有限差分格式[J].上海電機學院學報,2013,16(1/2): 88-92. [12] Samarskii A A.The Theory of Difference Schemes[M].New York: Marcel Dekker Inc,2001: 206. [13] Varga R S.Matrix Iterative Anaylsis[M].2nd ed.Berlin,Germany: Springer-Verlag,2000: 91. Monotone Iterative Algorithm of Compact Finite Difference Methodfor a Class of Elliptic Boundary Value Problems WUWenjia (Department of Mathematics and Physics, Shanghai Dianji University, Shanghai 201306, China) An effective monotone iterative algorithm is proposed for the fourth-order compact finite difference scheme of a class of two dimensional semi-linear elliptic boundary value problems. We analyze convergence rate of this iterative algorithm, give numerical results to show effectiveness of the algorithm. semi-linear elliptic boundary value problem; monotone iterative algorithm; convergence rate 2014 - 06 - 16 上海高校青年教師培養資助計劃項目資助(ZZSDJ13020) 武文佳(1985-),女,講師,博士,主要研究方向為偏微分方程數值解,Email: wuwj@sdju.edu.cn 2095 - 0020(2014)05 -0283 - 05 O 241.82 A

2 定義與引理

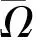

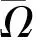




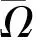
3 單調迭代算法





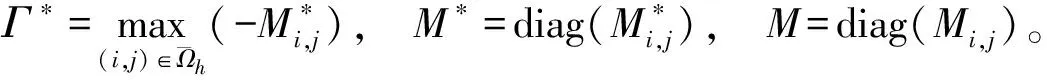



4 數值實驗