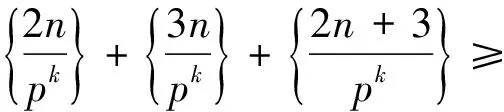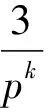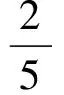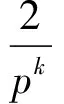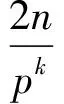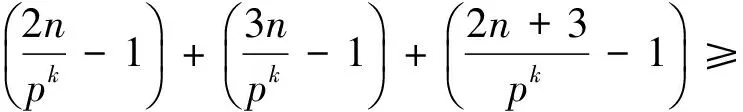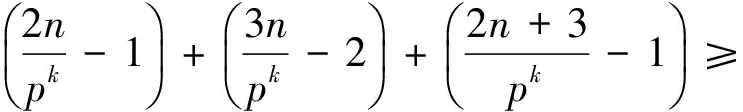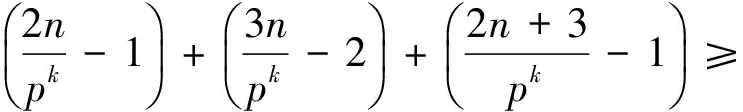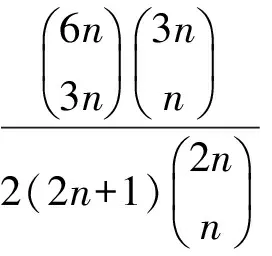中心二項式系數的同余性質

崔漢哲

(上海電機學院 數理教學部， 上海 201306)

中心二項式系數的同余性質

崔漢哲

(上海電機學院 數理教學部， 上海 201306)

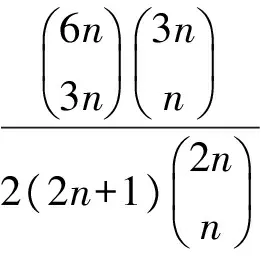
中心二項式系數;p進賦值函數; 同余性質

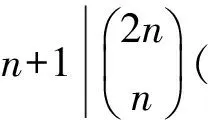
最近，孫智偉[14]證明了

1 定義與引理

引理1[14]對于任意正整數n都成立

定義1對于任意正整數n與素數p，定義p進賦值函數vp(n)為n的素因數分解中p的最高冪次。如對任意素數p有vp(1)=0，v3(9)=v3(36)=v2(36)=v2(4)等。

以下引理在任何一本數論的標準教材中都可以找到。如文獻[15]中的第一部分第一章的定理1.6。

引理2對于任意正整數n與素數p都有

2 定理及其證明

定理1Sn為奇數?n為2的冪次。

證明將Sn的分子與分母重新整理，得

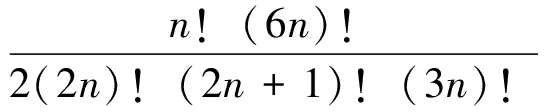
所要證者

v2(Sn)=v2(n!)+v2((6n)!)-v2((2n)!)-

v2((2n+1)!)-v2((3n)!)-1=0?n

為2的冪次。注意到

v2((2n+1)!)=v2((2n)!)=

v2(2·4…(2n-2)(2n))=v2(2nn!)=

n+v2(n!)

以及類似的

v2((6n)!)=3n+v2((3n)!)

可將v2(Sn)化簡為n-v2(n!)-1。以下分兩種情況，利用引理1具體計算該式。

(1) 當n=2l(l為非負整數)時，

2l-1=n-1

此即v2(Sn)=0。

(2) 當n不為2的冪次時，將n做二進制展開，即

n=2at+2at-1+…+2a0

其中，at>at-1>…>a0≥0且均為非負整數。因n不為2的冪次，故有t≥1。此時經簡單計算可得

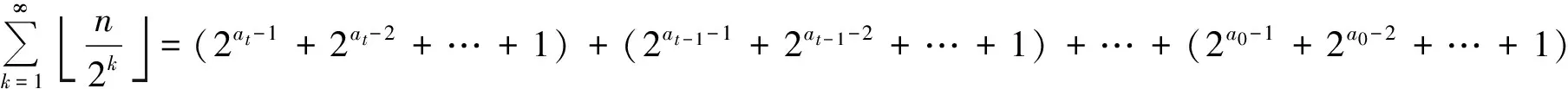
若a0=0，則(2a0-1+2a0-2+…+1)理解為0，

(2at-1-1)+…+(2a0-1)<

2at+2at-1+…+2a0-1=n

(注意到t≥1)

此即v2(Sn)>0。

證畢

定理2對任意正整數n，成立2n+3|3Sn。

證明經簡單計算，可得

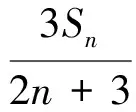
故所要證者即為對于任意素數p，都成立

vp(3)+vp((n+1)!)+vp((6n)!)≥

vp((2n)!)+vp((2n+3)!)+vp((3n)!)

(1)

也即

以下分p=2、p=3和p≥5三種情況討論。

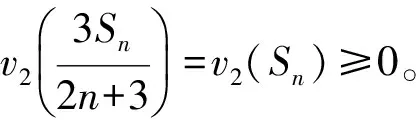
(2) 當p=3時，類似定理1中的證明，有

v3((6n)!)=2n+v3((2n)!)
v3((3n)!)=n+v3(n!)

成立，于是式(1)可簡化為

1+n+v3((n+1)!)≥v3(n!)+v3((2n+3)!)

再根據n模3的不同取值分3種情況討論(以下m均為自然數)。

①n=3m。經簡單計算可得式(1)不等號左邊=1+4m+v3(m!)，右邊=1+3m+v3(m!)+v3((2m+1)!)，故此時要證v3((2m+1)!)≤m。而

v3((2m+1)!)=

由于m為自然數，此即v3((2m+1)!)≤m。

②n=3m+1。經簡單計算可得式(1)不等號左邊=2+3m+v3((3m)!)，右邊=1+2m+v3((3m)!)+v3((2m+1)!)，故此時要證v3((2m+1)!)≤m+1。由①中結論，這顯然成立。

③n=3m+2。經簡單計算可得式(1)不等號左邊=4+4m+v3((m+1)!)，右邊=2+3m+v3(m!)+v3((2m+2)!)，故此時要證v3((2m+2)!)≤m+2+v3(m+1)。類似①中做法，有v3((2m+2)!)

(3) 當p≥5時，式(1)為

vp((n+1)!)+vp((6n)!)≥

vp((2n)!)+vp((2n+3)!)+vp((3n)!)

由引理1，只需證明對任意正整數k與n，均有

(2)

成立。

由于式(2)成立與否只依賴于n模pk的值，故以下設n=0,1,…,pk-1。然后，根據n+1,2n,2n+3,3n,6n與pk的不同大小關系逐一驗證式(2)成立。為討論方便，需要固定2n+3與3n的大小關系，即當n≥4時，有2n+3<3n。因此，n=0,1,2,3的情況首先單獨驗證。以下是具體過程(注意p≥5，k≥1)。

(1) 當n=0時，式(2)為

(2) 當n=1時，若p=5，且k=1，則式(2)為

其余情況下，式(2)均為

(3)n=2和n=3的情形與上文類似，本文省略具體過程。當n≥4時，分以下幾種情況具體計算可得：

① 當6n

② 當3n

③ 當2n+3

④ 當2n

⑧ 當pk≤n+1，即n=pk-1時，式(2)為

這樣便證明了對任意正整數k與n，式(2)均成立。

定理證畢

[1] Stanley R P.Enumerative Combinatorics: Vol.2[M].Cambridge： Cambridge University Press,1999: 219.

[2] Grimaldi R.Fibonacci and Catalan Numbers： An Introduction[M].New Jersey： John Wiley & Sons,2012: 147.

[3] Cao H Q，Pan H.Factors of alternating binomial sums[J].Advances in Applied Mathematics,2010,45： 96-107.

[4] Sun Zhiwei.Binomial coefficients,Catalan numbers and Lucas quotients[J].Science China Mathematics,2010,53： 2473-2488.

[5] Sun Zhiwei,Tauraso R.New congruences for central binomial coefficients[J].Advances in Applied Mathematics,2010,45： 125-148.

[6] Sun Zhiwei,Tauraso R.On some new congruences for binomial coefficients[J].International Journal of Number Theory,2011,7(3)： 645-662.

[7] Sun Zhiwei.On congruences related to central binomial coefficients[J].Journal of Number Theory,2011,131(11)： 2219-2238.

[8] Tauraso R.More congruences for central binomial coefficients[J].Journal of Number Theory,2010,130(12)： 2639-2649.

[9] Guo V J W,Zeng Jiang.Some congruences involving centralq-binomial coefficients[J].Advances in Applied Mathematics,2010,45(3)： 303-316.

[10] Mattarei S,Tauraso R.Congruences for central binomial sums and finite polylogarithms[J].Journal of Number Theory,2013,133(1)： 131-157.

[11] Sun Zhiwei.Supercongruences involving products of two binomial coefficients[J].Finite Fields and Their Applications,2013,22： 24-44.

[12] Sun Zhiwei.On divisibility of binomial coefficients[J].Journal of the Australian Mathematical Society,2012,93(1/2)： 189-201.

[13] Guo V J W,Krattenthaler C.Some divisibility properties of binomial andq-binomial coefficients[J].Journal of Number Theory,2014,135： 167-184.

[14] Sun Zhiwei.Products and sums divisible by central binomial coefficients. The Electronic Journal of Combinatorics,2013,20(1)： 9.

[15] 特倫鮑姆G.解析與概率數論導引[M].陳華一,譯.北京： 高等教育出版社，2011: 15.

Congruence Property of Central Binomial Coefficients

CUIHanzhe

(Department of Mathematics and Physics, Shanghai Dianji University, Shanghai 201306, China)

central binomial coefficients;p-adic valuation function; congruence property

2014 - 05 - 26

崔漢哲(1980-),男,講師，博士，主要研究方向為算子代數與組合數學，E-mail： cuihz@sdju.edu.cn

2095 - 0020(2014)05 -0288 - 04

O 151.1

A