奈特不確定下帶有紅利支付的養(yǎng)老金最優(yōu)投資策略

費(fèi)為銀，姚遠(yuǎn)浩，夏登峰

（安徽工程大學(xué) 數(shù)理學(xué)院，安徽 蕪湖 241000）

奈特不確定下帶有紅利支付的養(yǎng)老金最優(yōu)投資策略

費(fèi)為銀，姚遠(yuǎn)浩，夏登峰

（安徽工程大學(xué) 數(shù)理學(xué)院，安徽 蕪湖 241000）

研究帶有紅利支付的固定供款型養(yǎng)老基金的最優(yōu)投資問(wèn)題.在奈特不確定下，建立考慮紅利支付代理人的財(cái)富動(dòng)態(tài)方程，同時(shí)根據(jù)代理人對(duì)不同的公司存在不同的含糊程度，利用隨機(jī)控制理論刻畫代理人期望效用，得到Hamilton－Jacobi－Bellman（HJB）方程，通過(guò)求解HJB方程給出代理人最優(yōu)投資的顯式解，最后對(duì)結(jié)果進(jìn)行數(shù)值分析，定量分析了含糊和紅利支付因素對(duì)代理人最優(yōu)投資策略的影響.

含糊厭惡；紅利支付；固定供款；隨機(jī)控制；最優(yōu)投資策略

隨著世界人口老齡化趨勢(shì)的不斷加重，各國(guó)對(duì)養(yǎng)老金計(jì)劃越來(lái)越重視，養(yǎng)老金的規(guī)模也越來(lái)越大，因此，研究養(yǎng)老金的最優(yōu)投資問(wèn)題是很有必要的.養(yǎng)老金計(jì)劃主要分為固定供款型（DC）養(yǎng)老金計(jì)劃和固定受益型（DB）養(yǎng)老金計(jì)劃，隨著社會(huì)的發(fā)展，固定供款型養(yǎng)老金計(jì)劃成為養(yǎng)老保障的主流.有大量的文獻(xiàn)從不同角度對(duì)固定供款型養(yǎng)老金計(jì)劃的投資決策進(jìn)行了研究.文獻(xiàn)［1］研究了養(yǎng)老基金最低收益保障制度及其框架下的資產(chǎn)配置問(wèn)題.文獻(xiàn)［2］研究了當(dāng)工資為一個(gè)隨機(jī)過(guò)程時(shí)，繳費(fèi)確定型企業(yè)年金如何對(duì)股票、國(guó)債以及銀行存款進(jìn)行最優(yōu)資產(chǎn)配置的問(wèn)題.文獻(xiàn)［3－4］分別以財(cái)富水平的損失最小化和最終財(cái)富期望指數(shù)效用最大化作為目標(biāo)，研究固定供款型養(yǎng)老金最優(yōu)投資問(wèn)題.文獻(xiàn)［5］研究了仿射利率模型下固定供款型養(yǎng)老金的最優(yōu)投資問(wèn)題.但上述文獻(xiàn)沒(méi)有考慮投資過(guò)程中的不確定性因素，近年來(lái)，部分研究者在傳統(tǒng)的投資策略模型中考慮奈特（Knight）不確定性對(duì)投資模型帶來(lái)的影響.文獻(xiàn)［6］在奈特不確定性的情況下，描述了在不同的含糊水平下資產(chǎn)的最優(yōu)投資問(wèn)題.文獻(xiàn)［7］研究了無(wú)限壽命的投資者基于α－maxmin的預(yù)期CES效用偏好的最優(yōu)消費(fèi)－閑暇、投資組合和退休問(wèn)題，其中含糊（ambiguity）和含糊態(tài)度（ambiguity attitude）是區(qū)別開(kāi)來(lái)的.隨著對(duì)養(yǎng)老金研究的不斷深入，部分學(xué)者把奈特不確定性引入到對(duì)養(yǎng)老金的研究中.文獻(xiàn)［8］針對(duì)風(fēng)險(xiǎn)厭惡程度和不同的風(fēng)險(xiǎn)測(cè)度兩種情形，應(yīng)用動(dòng)態(tài)規(guī)劃原理研究養(yǎng)老金最優(yōu)投資策略.文獻(xiàn)［9］在奈特不確定的基金管理者區(qū)分含糊和含糊態(tài)度下，研究了帶有最低保障固定供款型養(yǎng)老基金最優(yōu)管理問(wèn)題.文獻(xiàn)［10］考慮對(duì)不同公司有不同含糊厭惡的代理人對(duì)固定供款型養(yǎng)老金的最優(yōu)投資問(wèn)題.公司的股票分紅也是影響投資者決策的重要因素，文獻(xiàn)［11］討論了遞推多先驗(yàn)效用（含糊厭惡）下的比例再保險(xiǎn)和紅利優(yōu)化問(wèn)題.文獻(xiàn)［12］研究了帶有遞歸偏好的投資者在考慮股票紅利支付情形下的最優(yōu)消費(fèi)和投資組合問(wèn)題.

本文在文獻(xiàn)［10］的基礎(chǔ)上加入紅利支付這一影響因子，同時(shí)考慮含糊厭惡和紅利支付雙重因素對(duì)固定供款型養(yǎng)老金投資的影響.首先，假設(shè)代理人是含糊厭惡的，根據(jù)投資者對(duì)不同的公司存在不同的含糊程度，刻畫出代理人的期望效用，然后，建立代理人帶有股票紅利支付的財(cái)富動(dòng)力學(xué)方程，接著建立關(guān)于投資者效用最大化的問(wèn)題Hamilton－Jacobi－Bellman（HJB）方程，再求解 HJB方程得到最優(yōu)投資策略，并通過(guò)數(shù)值模擬對(duì)所得結(jié)論進(jìn)行相關(guān)經(jīng)濟(jì)學(xué)分析.

1 模型框架和基本假設(shè)

在固定供款型養(yǎng)老金計(jì)劃中，代理人要對(duì)資產(chǎn)進(jìn)行投資增值.假設(shè)代理人將資產(chǎn)分為兩部分投資：一部分投資在無(wú)風(fēng)險(xiǎn)資產(chǎn)上，確保穩(wěn)定收益；另一部分投資在風(fēng)險(xiǎn)資產(chǎn)上，希望獲得更大的收益.代理人在對(duì)風(fēng)險(xiǎn)資產(chǎn)進(jìn)行投資時(shí)只選擇股票進(jìn)行投資.為了便于討論，只考慮兩家公司的兩只股票，且這兩家公司有類似的生產(chǎn)技術(shù)，那么他們的股票價(jià)格Yit就滿足

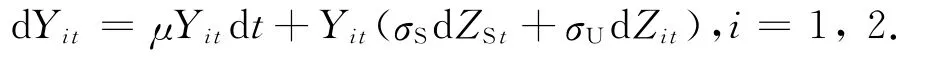
其中：μ為期望回報(bào)率；σS為系統(tǒng)風(fēng)險(xiǎn)波動(dòng)率；σU為非系統(tǒng)風(fēng)險(xiǎn)波動(dòng)率；t為時(shí)刻；ZSt為系統(tǒng)風(fēng)險(xiǎn)；Zit為非系統(tǒng)風(fēng)險(xiǎn).ZSt和Zit是彼此相互獨(dú)立的一維布朗運(yùn)動(dòng).

本文針對(duì)公司1的代理人進(jìn)行以下的研究.用下標(biāo)1表示公司1的一個(gè)代理人投資在自己公司股票的狀態(tài)，用下標(biāo)2表示公司1的代理人投資另外一家公司股票的狀態(tài).假設(shè)代理人對(duì)兩家公司股票回報(bào)率的分布都是不確定的，代理人對(duì)自己公司的含糊程度用φ1表示，對(duì)另外一家公司的含糊程度用φ2表示，其中φ1未必等于φ2.

根據(jù)文獻(xiàn)［10］，假設(shè)代理人是含糊厭惡的，且他的生命是無(wú)限的，那么他在t時(shí)刻的期望效用Ut表達(dá)式為

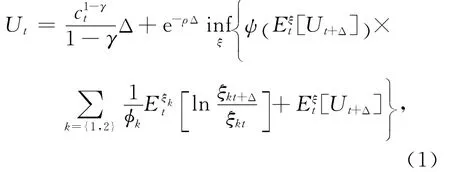
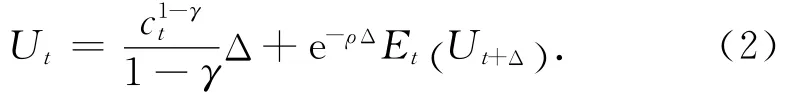
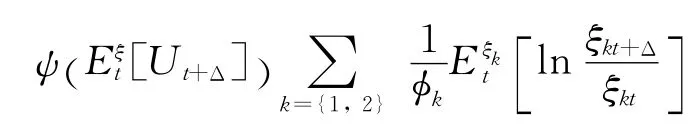
根據(jù)文獻(xiàn)［13］，令式（1）中的Δ趨近于0，則連續(xù)時(shí)間情形下的效用函數(shù)可以寫成

由于代理人對(duì)自己公司和另外一家公司的含糊程度不同，因此投資到兩家公司股票的資產(chǎn)也不同.令π1和π2分別表示投資到兩家公司股票的財(cái)富值比例，π1和π2可以不相等.代理人最優(yōu)投資組合的累計(jì)回報(bào)為

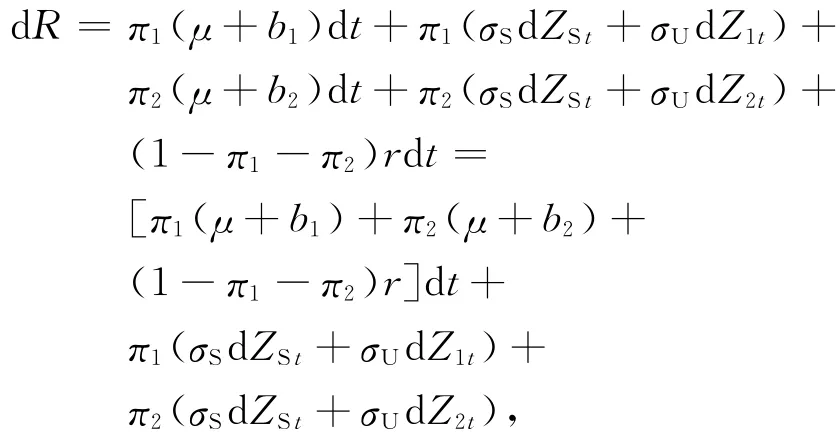
其中：r為無(wú)風(fēng)險(xiǎn)利率，b1和b2分別為兩家公司的股票分紅.將代理人最優(yōu)投資組合的累計(jì)回報(bào)分為3個(gè)組成部分：投資在自己公司股票、投資在另外一家公司股票和投資在無(wú)風(fēng)險(xiǎn)資產(chǎn)，那么前兩項(xiàng)的協(xié)方差矩陣為

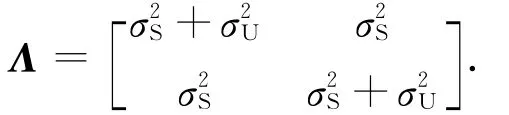
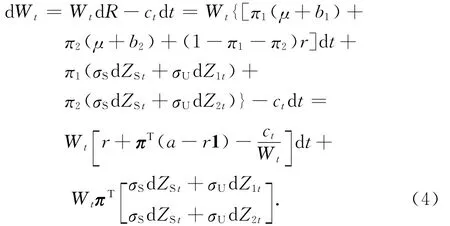
設(shè)V（t，Wt）表示代理人在t時(shí)刻的值函數(shù)，根據(jù)式（3）有

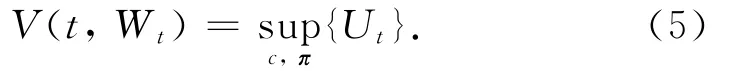
2 最優(yōu)投資策略

根據(jù)式（1）、（4）和（5）得到代理人的 HJB方程（證明略）為

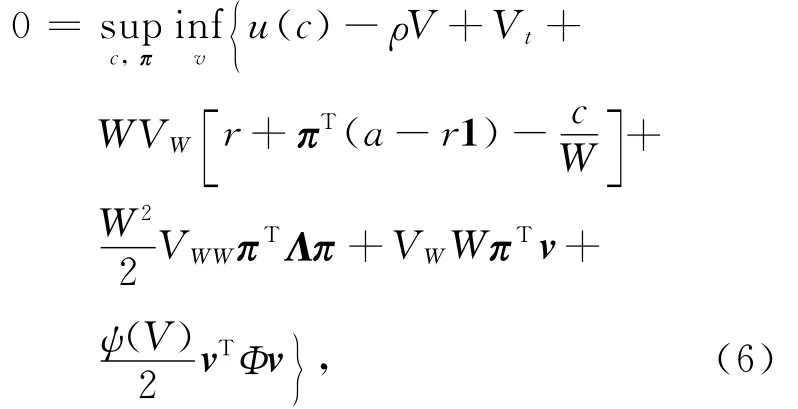
其中：Vt，VW，VWW分別表示V（·）關(guān)于相應(yīng)變量的一階偏導(dǎo)數(shù)和二階偏導(dǎo)數(shù)，

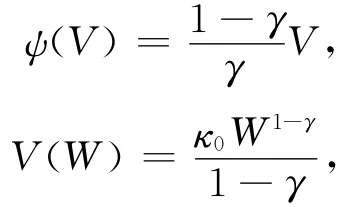
其中：κ0為常數(shù).下面求解最優(yōu)投資策略.

式（6）對(duì)v求偏導(dǎo)得

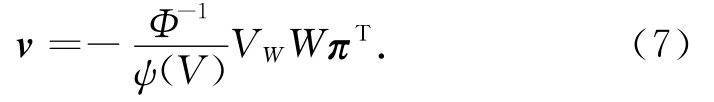
將式（7）代入式（6），HJB方程變?yōu)?/p>

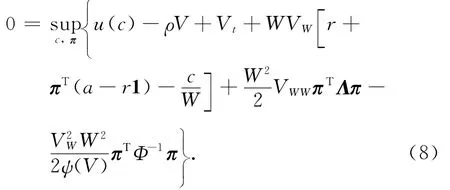
式（8）對(duì)π求偏導(dǎo)得

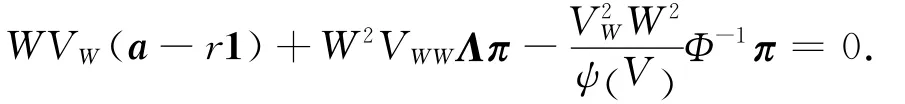
由于

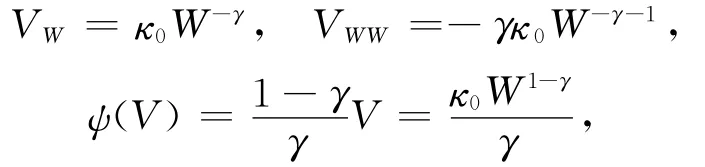
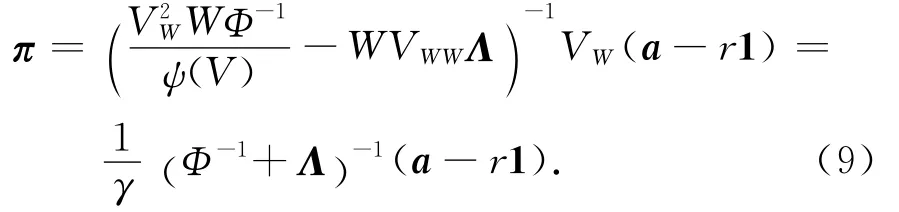
所以把Λ和Φ代入式（9）中，整理得最優(yōu)的投資比例，于是有下面的命題.

命題1 在上述模型假設(shè)下，最優(yōu)投資策略為

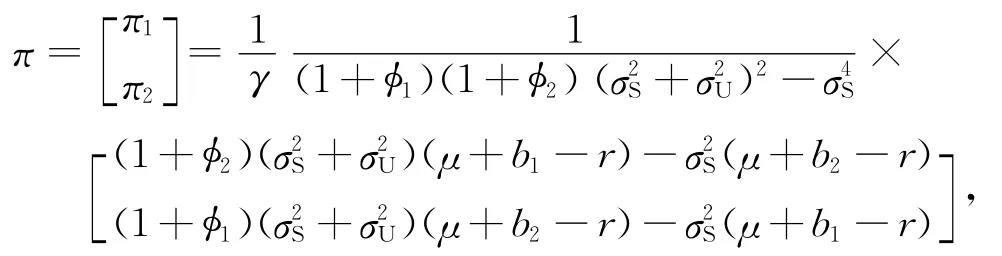
其中：π1表示代理人投資在自家公司股票上的財(cái)富比例；π2表示代理人投資在另外一家公司股票上的財(cái)富比例.由命題1易知如下結(jié)論.

命題2 當(dāng)不存在含糊時(shí)，即φ1＝φ2＝0，標(biāo)準(zhǔn)的投資組合權(quán)重為

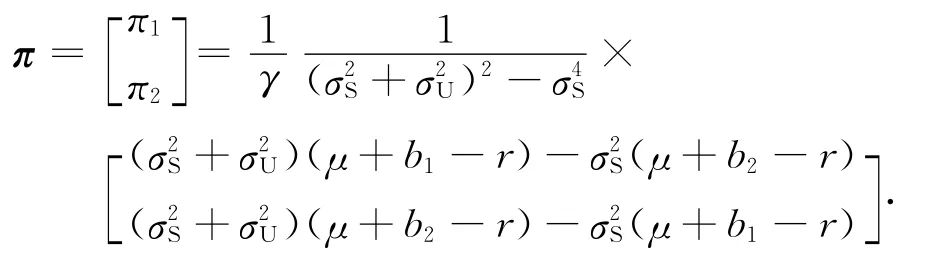
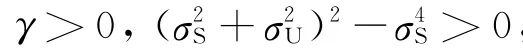
命題3 當(dāng)代理人對(duì)自己公司存在含糊，而對(duì)另外一家公司極度含糊時(shí)，即φ1＞0，φ2→∞，投資組合的權(quán)重近似為

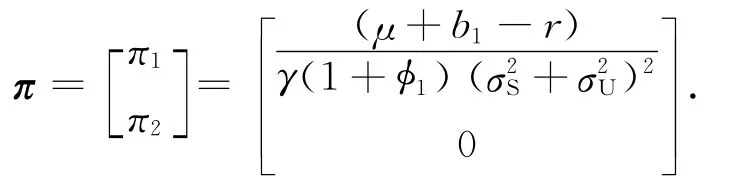
從命題3可以看出，當(dāng)代理人對(duì)另外一家公司極度含糊時(shí)，代理人將所有投資在風(fēng)險(xiǎn)資產(chǎn)上的財(cái)富值都投在自己公司股票上，而且隨著自己公司分紅的增加，投資在自己公司股票的財(cái)富比例也增加.

命題4 當(dāng)代理人對(duì)另外一家公司存在含糊，而對(duì)自己公司極度含糊時(shí)，即φ2＞0，φ1→∞，投資組合的權(quán)重近似為

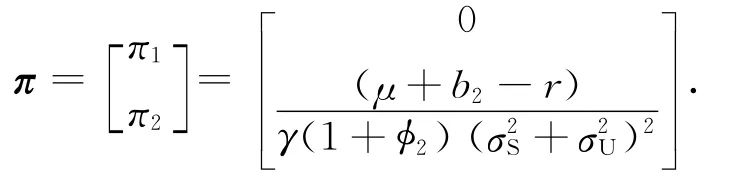
由命題4可以看出，當(dāng)代理人對(duì)自己公司極度含糊時(shí)，代理人將所有投資在風(fēng)險(xiǎn)資產(chǎn)上的財(cái)富都投在另外一家公司股票上，而且隨著另外一家公司分紅的增加，投資在另外一家公司股票的財(cái)富比例也增加.

命題5 當(dāng)代理人對(duì)自己公司和另外一家公司都極度含糊時(shí)，即φ1→∞，φ2→∞，投資組合的權(quán)重近似為

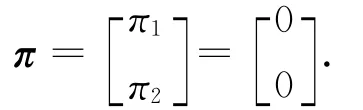
由命題5可知，代理人將不會(huì)在風(fēng)險(xiǎn)資產(chǎn)上投資，他將會(huì)把所有的財(cái)富值都投資在無(wú)風(fēng)險(xiǎn)資產(chǎn)上.

3 數(shù)值分析

本文通過(guò)數(shù)值模擬說(shuō)明含糊和股票分紅對(duì)代理人動(dòng)態(tài)資產(chǎn)配置的影響.根據(jù)命題1，令φ1＝0.5，γ＝1，σS＝0.2，σU＝0.3，b1＝0.01，b2＝0.01，μ－r＝0.07，考察φ2對(duì)資產(chǎn)組合權(quán)重的影響，結(jié)果如圖1所示.

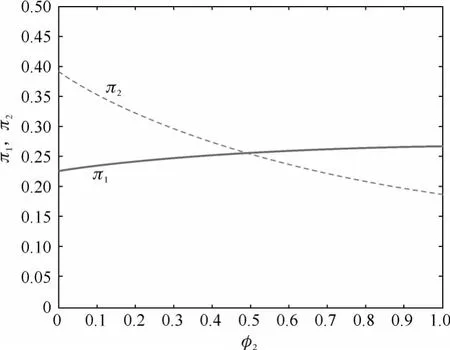
圖1 φ2對(duì)資產(chǎn)組合權(quán)重π的影響Fig.1 Effect ofφ2on optimal portfolioπ

從圖1可以看出，π1隨著φ2的增加而增加，π2隨著φ2的增加而減少.由于設(shè)定兩公司的股票分紅都是相同的，因此，在φ2＝0，即代理人對(duì)另外一家公司極其了解，而對(duì)自己公司存在含糊，代理人在另外一家公司上的投資比例高于在自己公司上的投資比例.隨著對(duì)另外一家公司含糊的增加，在另外一家公司的投資就會(huì)減少，相反，在自己公司的投資相應(yīng)地增加，直到兩公司的厭惡程度相同時(shí)，即φ1＝φ2＝0.5時(shí)，代理人在兩公司上的投資比例相同.隨著對(duì)另外一家公司的含糊程度越來(lái)越大，投資在另外一家公司的資產(chǎn)比例就會(huì)越來(lái)越小，投資在自己公司的資產(chǎn)比例就會(huì)越來(lái)越大.從圖1還可以看到，隨著φ2的不斷增加，π1和π2之和越來(lái)越小，這是因?yàn)榇砣藢?duì)自己公司的含糊是固定的，隨著對(duì)另外一家公司含糊的增加，他對(duì)整個(gè)風(fēng)險(xiǎn)資產(chǎn)上的含糊也相應(yīng)增加，那么就會(huì)減少在風(fēng)險(xiǎn)資產(chǎn)上的投資.

根據(jù)命題3，令φ2＝10 000，γ＝1，σS＝0.2，σU＝0.3，b1＝0.01，b2＝0.01，μ－r＝0.07，考察φ1對(duì)資產(chǎn)組合權(quán)重的影響，結(jié)果如圖2所示.從圖2可以看出，π2幾乎一直為0，π1隨著φ1的增加而減少.代理人由于是含糊厭惡的，所以當(dāng)對(duì)另外一家公司的含糊十分大時(shí)，不管φ1怎么變化，代理人都不會(huì)對(duì)其投資.隨著自己公司含糊的增加，投資在自己公司上的財(cái)富比例一直減少，直到自己公司的含糊無(wú)限大時(shí)，代理人投資在自己公司上的財(cái)富比例減為0，這時(shí)，代理人只會(huì)將財(cái)富投資在無(wú)風(fēng)險(xiǎn)資產(chǎn)上.

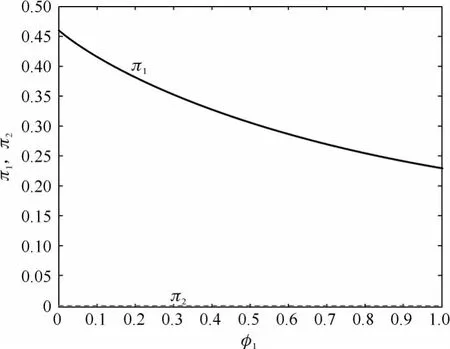
圖2 φ2→∞時(shí)，φ1對(duì)資產(chǎn)組合權(quán)重π的影響Fig.2 φ2→∞，Effect ofφ1on optimal portfolioπ

根據(jù)命題1，令γ＝1，σS＝0.2，σU＝0.3，b1＝0.01，b2＝0.01，μ－r＝0.07，考察φ1和φ2同時(shí)變化對(duì)投資到自己公司股票的財(cái)富值比例的影響，結(jié)果如圖3所示.從圖3可以看出，隨著φ1的增加，π1逐漸減小，隨著φ2的增加π1逐漸增加.當(dāng)對(duì)自己公司的含糊程度最大而對(duì)另外一家公司沒(méi)有含糊時(shí)，代理人投資在自己公司的財(cái)富比例最小，即φ1＝1，φ2＝0時(shí)，π1最小.當(dāng)對(duì)另外一家公司的含糊程度最大而對(duì)自己公司沒(méi)有含糊時(shí)，代理人投資在自己公司的財(cái)富比例最大，即φ1＝0，φ2＝1時(shí)，π1最大.這和實(shí)際的經(jīng)濟(jì)情況是吻合的.

圖3 φ1和φ2同時(shí)變化對(duì)π1的影響Fig.3 Effect ofφ1andφ2on optimal portfolioπ1

根據(jù)命題1，令φ2＝0.5，γ＝1，σS＝0.2，σU＝0.3，b2＝0.01，μ－r＝0.07.考察φ1和自己公司的股票分紅b1同時(shí)變化對(duì)投資到自己公司股票的財(cái)富值比例的影響，結(jié)果如圖4所示.從圖4可以看到，投資到自己公司上的財(cái)富比例π1隨著b1的增加而不斷增加，隨著對(duì)自己公司含糊程度φ1的增加而不斷減小.當(dāng)φ1＝1，b1＝0.02時(shí)，π1取最小值，即圖4中的最低點(diǎn).當(dāng)φ1＝0，b1＝1時(shí)，π1取最大值，即圖4中最高點(diǎn).在投資過(guò)程中，投資者會(huì)盡量避免在那些自己不了解并且收益差的資產(chǎn)上投資，而選擇投資在那些自己了解且收益好的資產(chǎn)上，圖4中正好體現(xiàn)了這一點(diǎn).在實(shí)際經(jīng)濟(jì)活動(dòng)中，大部分公司都會(huì)通過(guò)各種途徑的宣傳來(lái)提高知名度，從而減小投資者對(duì)其公司的含糊程度，另外上市公司還會(huì)通過(guò)股票紅利支付來(lái)提高投資者的收益，這兩種方法都可以為公司帶來(lái)更多的投資.

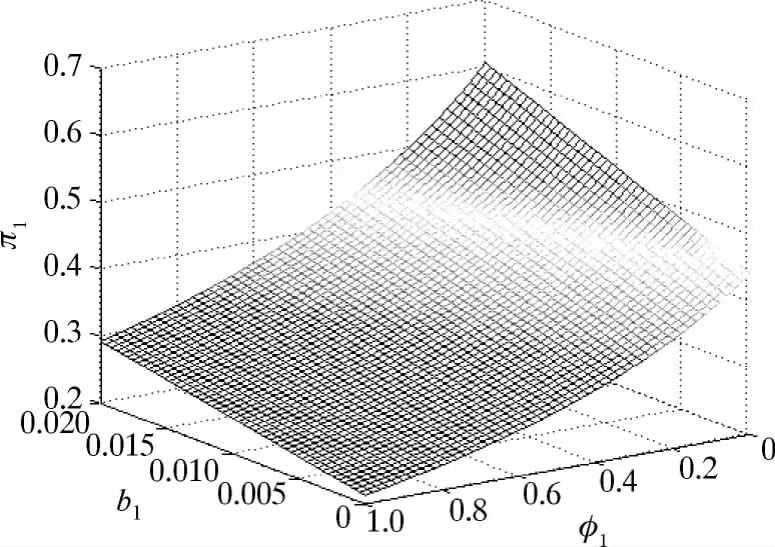
圖4 b1和φ1同時(shí)變化對(duì)π1的影響Fig.4 Effect of b1andφ1on optimal portfolioπ1

4 結(jié) 語(yǔ)

本文在奈特不確定下，考慮自己公司和另外一家公司不同含糊程度和股票紅利支付這兩種因素對(duì)固定供款型養(yǎng)老金最優(yōu)投資的影響，借助隨機(jī)微分方程和隨機(jī)控制理論，得到代理人的最優(yōu)投資組合，并通過(guò)數(shù)值分析分別說(shuō)明了自己公司的含糊程度、另外一家公司的含糊程度以及股票紅利支付對(duì)投資組合的影響.本文通過(guò)模型的顯式解以及數(shù)值分析可知：當(dāng)自己公司含糊程度增加時(shí)，代理人投資自己公司的財(cái)富比例就會(huì)減少，投資到另外一家公司財(cái)富比例會(huì)增加；當(dāng)自己公司股票分紅增加時(shí)，代理人投資到自己公司的財(cái)富比例會(huì)增加，投資到另外一家公司的財(cái)富比例會(huì)減少.這與實(shí)際經(jīng)濟(jì)活動(dòng)是十分相符的，由此說(shuō)明本文的模型具有較為重要的實(shí)際經(jīng)濟(jì)意義.

本文也將在以下兩個(gè)方面進(jìn)一步拓展：首先，本文僅考慮兩種風(fēng)險(xiǎn)資產(chǎn)，以后會(huì)將其拓展到多個(gè)資產(chǎn)上進(jìn)行研究；其次，本文只是考慮含糊厭惡型代理人，沒(méi)有考慮含糊喜好型代理人，而實(shí)際生活中確實(shí)存在一些含糊喜好投資者.更為一般地，當(dāng)代理人具有極大極小期望效用時(shí)，投資策略將如何變化，將有待進(jìn)一步研究.

參 考 文 獻(xiàn)

［1］劉富兵，劉海龍，周穎.養(yǎng)老基金最低收益保證制度下的最優(yōu)資產(chǎn)配置［J］.財(cái)經(jīng)研究，2008，34（9）：112－121.

［2］卞世博.隨機(jī)工資下DC型企業(yè)年金的最優(yōu)資產(chǎn)配置策略［J］.會(huì)計(jì)與經(jīng)濟(jì)研究，2012（3）：57－66.

［3］GERRARD R， HABERMAN S， VIGNA E. Optimal investment choices post retirement in a defined contribution pension scheme［J］.Insurance：Mathematics and Economics，2004，35（2）：321－342.

［4］林祥，楊益非.Heston隨機(jī)方差模型下確定繳費(fèi)型養(yǎng)老金的最優(yōu)投資［J］.應(yīng)用數(shù)學(xué)，2010，23（2）：413－418.

［5］張初兵，榮喜民.仿射利率模型下確定繳款型養(yǎng)老金的最優(yōu)投資［J］.系統(tǒng)工程理論與實(shí)踐，2012，32（5）：1049－1056.

［6］UPPAL R，WANG T.Model misspecification and underdiversification［J］.The Journal of Finance，2003，58（6）：2465－2486.

［7］FEI W Y. Optimal consumption－leisure， portfolio and retirement selection based onα－maxmin expected CES utility with ambiguity［J］.Applied Mathematics：A Journal of Chinese Universities，2012，27（4）：435－454.

［8］HABERMAN S，VIGNA E.Optimal investment strategies and risk measure in defined contribution pension schemes［J］.Insurance：Mathematics and Economics，2002，31（1）：35－69.

［9］石學(xué)芹，費(fèi)為銀，李娟，等.奈特不確定環(huán)境下固定供款型養(yǎng)老基金最優(yōu)投資策略研究［J］.中國(guó)科學(xué)技術(shù)大學(xué)學(xué)報(bào)，2014，44（3）：188－193，226.

［10］BOYLE P，UPPAL R，WANG T.Ambiguity aversion and the puzzle of own－company stock in pension plans［R］.Working Paper，2003，http：／／www.cepr.org／meets／wkcn／5／593／papers／uppal.pdf.

［11］夏登峰，費(fèi)為銀，梁勇.帶含糊厭惡的股東價(jià)值最大化［J］.中國(guó)科學(xué)技術(shù)大學(xué)學(xué)報(bào)，2010，40（9）：920－924.

［12］楊武，費(fèi)為銀，潘磊.模型不確定下帶紅利支付的最優(yōu)消費(fèi)和投資組合［J］.東華大學(xué)學(xué)報(bào)：自然科學(xué)版，2013，39（3）：380－384.

［13］JIN X，ZHANG A.Ambiguity aversion，optimal portfolio choice and market decomposition with rare events ［R］.Working Paper，2011，http：／／www.ccfr.org.cn／cicf2011／papers／20110523013543.pdf.

Optimal Investment Strategy for Pension with Dividend Payment under Knightian Uncertainty

FEIWei－yin，YAOYuan－h(huán)ao，XIADeng－feng
（School of Mathematics and Physics，Anhui Polytechnic University，Wuhu Anhui 241000，China）

An optimal investment strategy for defined contribution pension plan with dividend payment is investigated.First，an agent's wealth dynamic equation with dividend payment is established under Knight uncertainty.At the same time，the agent's expected utility function is characterized by the stochastic control theory，where the agent has different levels of ambiguity aversion to different companies.Then，the Hamilton－Jacobi－Bellman（HJB）equation is got.By solving the HJB equation，the explicit form solutions of the optimal investment strategy is obtained.Finally，the impact of the ambiguity and the dividend payment on the optimal investment strategy of an agent is analyzed through a numerical simulation.

ambiguity aversion；dividend payment；defined contribution；stochastic control；optimal investment strategy

F 224.9

A

1671－0444（2014）04－0497－06

2013－07－01

國(guó)家自然科學(xué)基金資助項(xiàng)目（71171003，71271003）；教育部人文社會(huì)科學(xué)規(guī)劃基金資助項(xiàng)目（12YJA790041）；安徽省自然科學(xué)基金資助項(xiàng)目（090416225，1208085MG116）；安徽省高校自然科學(xué)基金資助項(xiàng)目（KJ2012B019，KJ2013B023）

費(fèi)為銀（1963—），男，安徽蕪湖人，教授，博士，研究方向?yàn)榻鹑跀?shù)學(xué)與金融工程、隨機(jī)控制.E－mail：wyfei＠ahpu.edu.cn