滾翼機滾轉階躍響應分析

杜帆, 胡峪

(西北工業大學 航空學院, 陜西 西安 710072)

0 引言

無人飛行器具有起降要求簡單、隱身性能優異、機動性能突出等特點,近年來在軍用及民用領域扮演著重要角色。滾翼機[1]作為一種全新類型的飛行器,近年來成為航空界的新興研究熱點。

目前對于滾翼機的研究尚處在初級階段,總體參數對于滾翼機穩定性的影響尚未得到準確分析。本文提出滾翼機的動力學模型,通過仿真分析影響其滾轉穩定性的因素,合理解釋了驗證機試飛過程中出現的三軸力矩耦合現象。

1 飛行器總體布局

滾翼機是一種由擺線槳提供升力的新型可垂直起降飛行器。在低雷諾數條件下,擺線槳具備高效率、高機動性的特點[1-3]。

滾翼機采用三軸式總體布局(見圖1),機身前部安裝有兩個同向旋轉的擺線槳,機身尾部安裝有一個螺旋槳。兩擺線槳產生升力的方向始終垂直于機身,升力大小由其轉速決定。

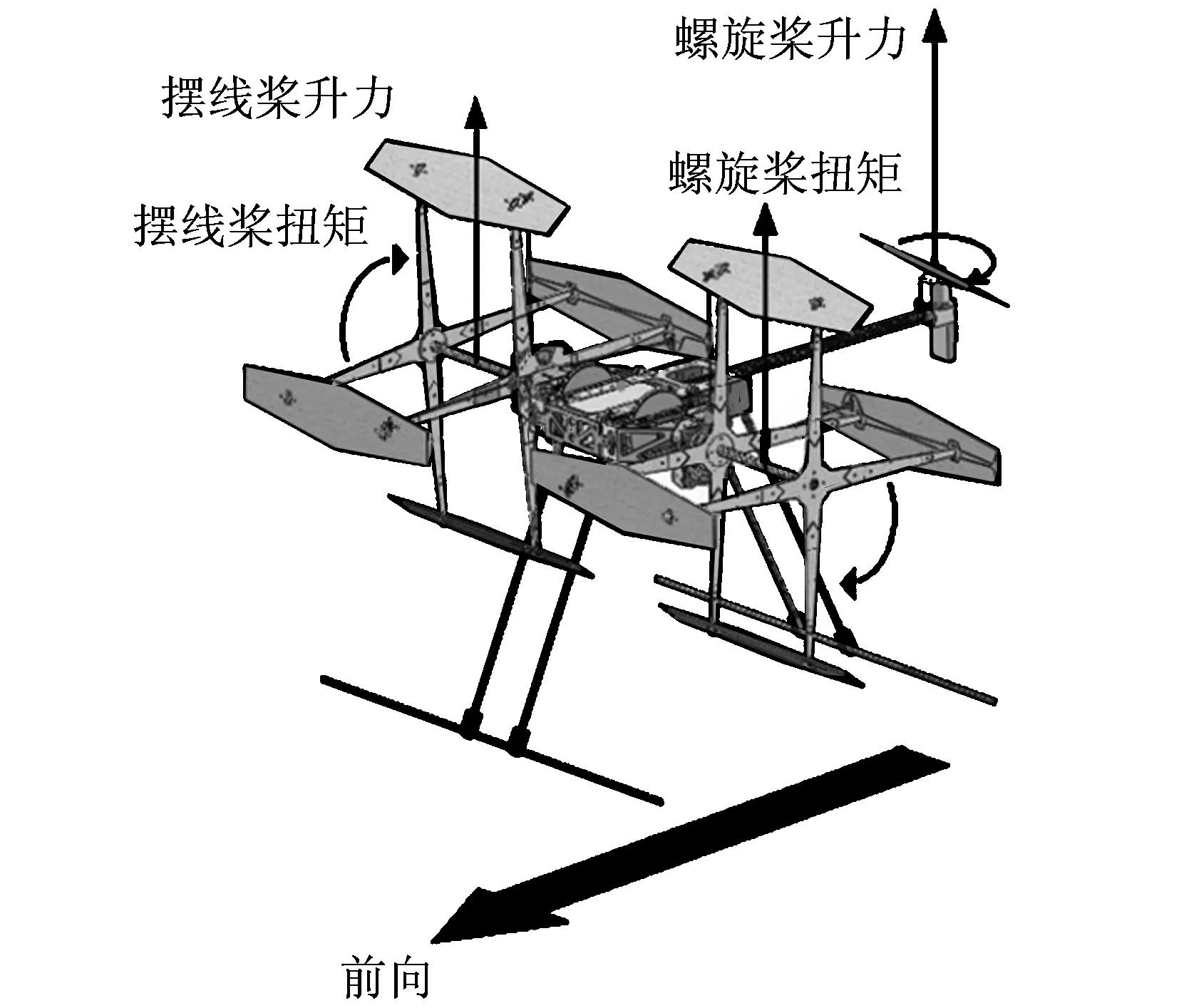
圖1 滾翼機總體布局圖Fig.1 Configuration of three-rotor cyclogyro

滾翼機受力分析如圖2所示,兩擺線槳的合力作為主要升力,控制滾翼機的上升和下降;兩擺線槳的差動產生滾轉力矩,控制滾翼機的滾轉運動。尾部螺旋槳能夠圍繞尾桿進行左右偏轉(見圖3),垂直于機身的升力分量控制滾翼機的俯仰運動,平行于機身的升力分量控制滾翼機的偏航運動(見圖4)。圖中,F1,F2,T1,T2,ω1,ω2分別為左、右擺線槳的升力、扭矩、角速度;Ft,Tt,ωt分別為尾部螺旋槳的升力、扭矩、角速度;Gx,Gy,Gz分別為重力沿體軸系的分量;L1為擺線槳葉片中心到飛行器對稱面的距離;L2為擺線槳旋轉軸到飛行器重心cg的水平距離;L3為尾部螺旋槳旋轉軸到飛行器重心的水平距離;L4為螺旋槳槳盤到尾桿旋轉軸的距離;α為尾部螺旋槳的偏轉角;h1為擺線槳旋轉軸到飛行器重心的垂直距離;h2為尾桿旋轉軸到飛行器重心的垂直距離。

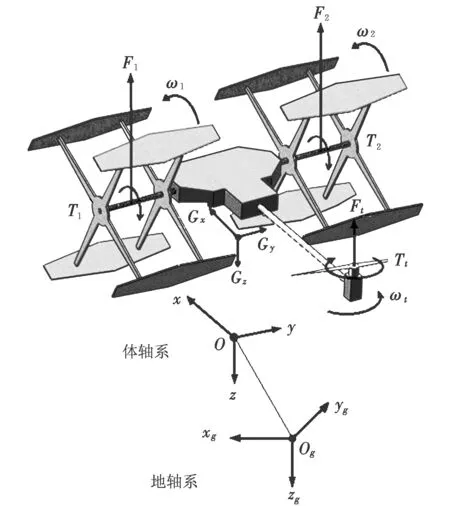
圖2 滾翼機受力分析圖Fig.2 Forces and moments acting on cyclogyro

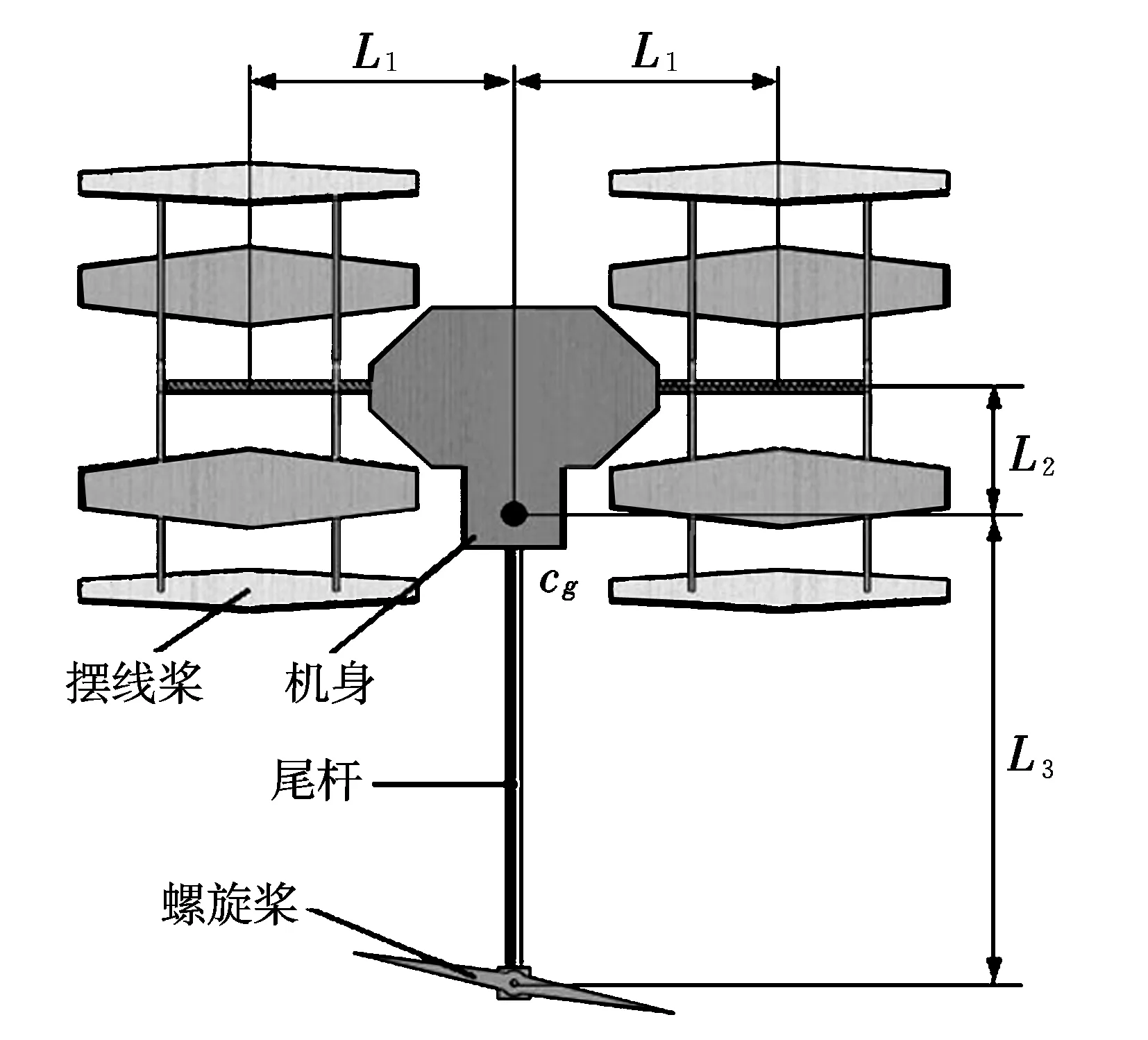
圖3 滾翼機俯視圖Fig.3 Bottom view of the dynamic model

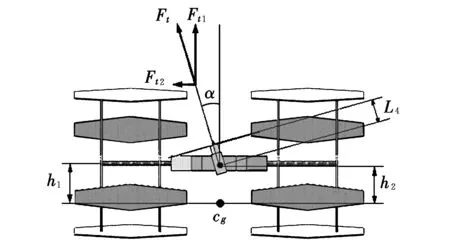
圖4 滾翼機后視圖Fig.4 Back view of the dynamic model

2 建立動力學模型

結合滾翼機受力分析,計算得到滾翼機在體軸系下所受到的合力及合力矩為:

∑Fx=-mgsinθ

∑Fy=mgcosθsinφ-Ftsinα

∑Fz=mgcosθcosφ-Ftcosα-F1-F2

∑Mx=F1L1-F2L1+Mgcr1+Mgcr2+Mgtr-

Ft2(h2+L4cosα)+Ft1L4sinα

∑My=F1L2+F2L2-Ft1L3+T1+T2+Mgtp

∑Mz=Ft2L3+Tt+Mgcy1+Mgcy2

式中,Mgcr為滾翼機在偏航時擺線槳產生的滾轉力矩;Mgtr為滾翼機在俯仰時螺旋槳產生的滾轉力矩;Mgtp為滾翼機在滾轉時螺旋槳產生的俯仰力矩;Mgcy為滾翼機在滾轉時擺線槳產生的偏航力矩。

綜合以上方程式,在體軸系下建立滾翼機的動力學模型[4],具體表示如下:

式中,Rij為體軸系到地軸系的轉換矩陣R的元素[5];Ix,Iy,Iz分別為滾翼機相對Ox軸、Oy軸、Oz軸的轉動慣量。

3 仿真分析

根據所建立的動力學方程,對滾翼機進行動力學仿真,并對仿真結果進行分析。仿真過程為:滾翼機在第0～10 s處于初始穩定狀態(滾轉角、滾轉角速度、俯仰角、俯仰角速度、偏航角、偏航角速度均為零),在第10 s輸入-5°階躍滾轉角,滾翼機保持給定滾轉角達到穩定狀態(滾轉、俯仰、偏航角速度均為零)。

3.1 飛行器懸停仿真分析

仿真結果顯示,滾翼機在初始穩定階段始終存在沿Ogyg軸的橫向位移。受力分析如圖5所示,尾槳在提供航向分力Ft2以抵消尾槳反扭矩Tt的同時,該分力Ft2使飛行器產生沿Ogyg軸向位移。因此滾翼機欲實現穩定定點懸停,機體必須保持一定的滾轉角,這與普通直升機的懸停特點相似。

圖5 滾翼機橫向平移分析Fig.5 Analysis of cyclogyro translation

3.2 尾槳參數仿真分析

尾槳產生的升力作用于螺旋槳的槳盤中心,其相對于飛行器重心的距離由參數α,L4和h2決定。其中α是飛控系統控制參數,因此決定尾槳位置的幾何參數主要為L4和h2。

仿真結果顯示,參數L4的變化對于滾翼機的飛行穩定性能沒有顯著影響。該現象可由受力分析圖(見圖6)進行解釋。

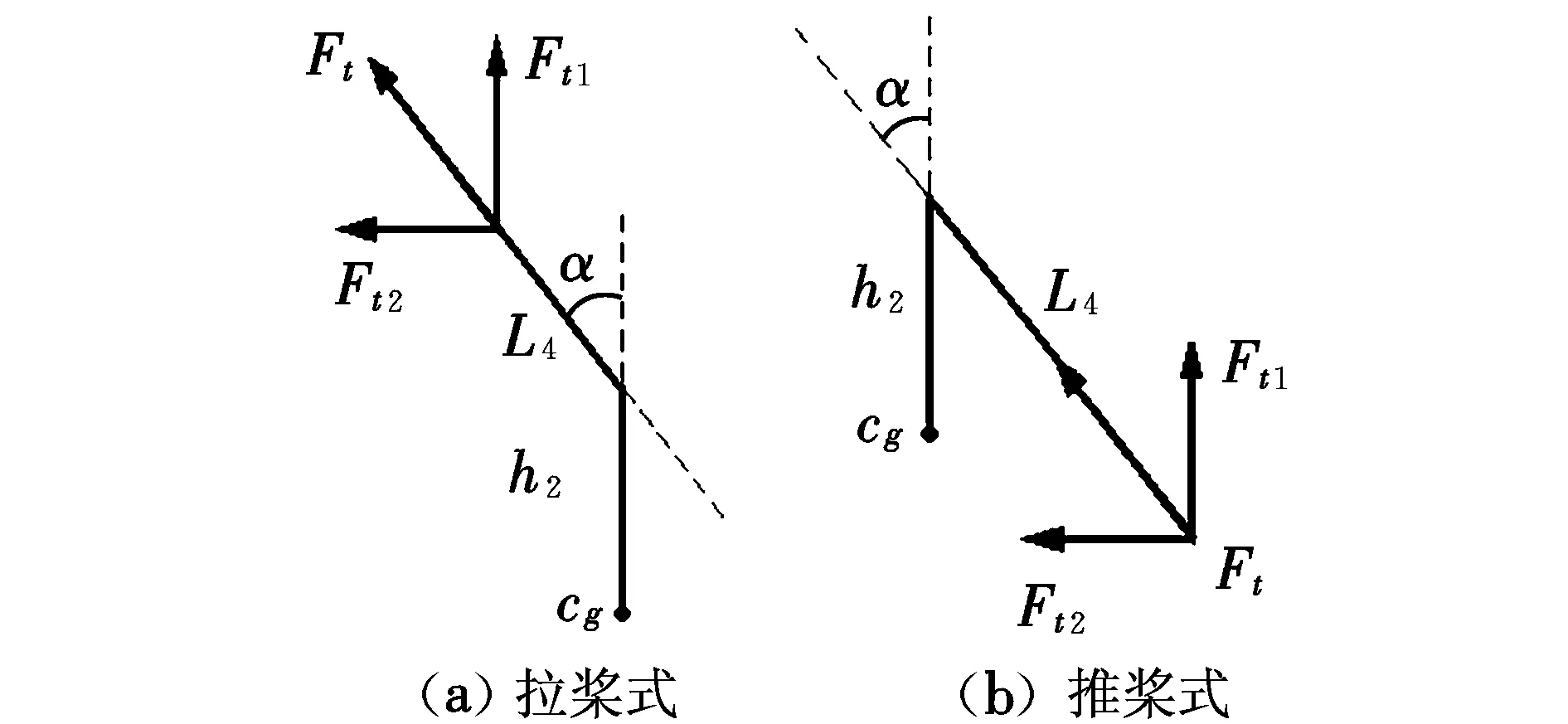
圖6 尾槳受力分析簡化圖Fig.6 Forces of back view on cyclogyro

尾部螺旋槳在偏轉過程中產生沿垂直方向和水平方向的兩個分力Ft1,Ft2,同時兩分力的作用力臂也隨偏轉發生改變。根據圖6所示,尾槳的滾轉合力矩∑Mt可表示為:

∑Mta=Ft2(L4cosα+h2)-Ft1L4sinα

=Ftsinαh2

=Ft2h2

∑Mtb=Ft1L4sinα+Ft2(h2-L4cosα)

=Ftsinαh2

=Ft2h2

由上述方程式可知，尾槳的滾轉合力矩均為∑Mt=Ft2h2。因此,尾槳產生的滾轉力矩僅與尾槳升力的水平分量Ft2及重心相對尾桿的距離h2相關。尾部螺旋槳槳盤相對尾桿的距離L4對于滾翼機的滾轉沒有影響,即等效于尾部螺旋槳產生的升力直接作用于尾桿上。

此外,還需對參數h2進行仿真分析。h2分別取值為:h2=+4 cm,h2=0 cm,h2=-4 cm(尾桿高于重心時為正值)。仿真結果如圖7～圖11所示。

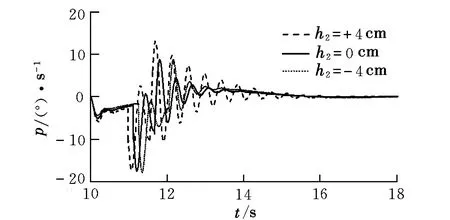
圖7 滾翼機滾轉角速度曲線Fig.7 Roll angular velocity of cyclogyro

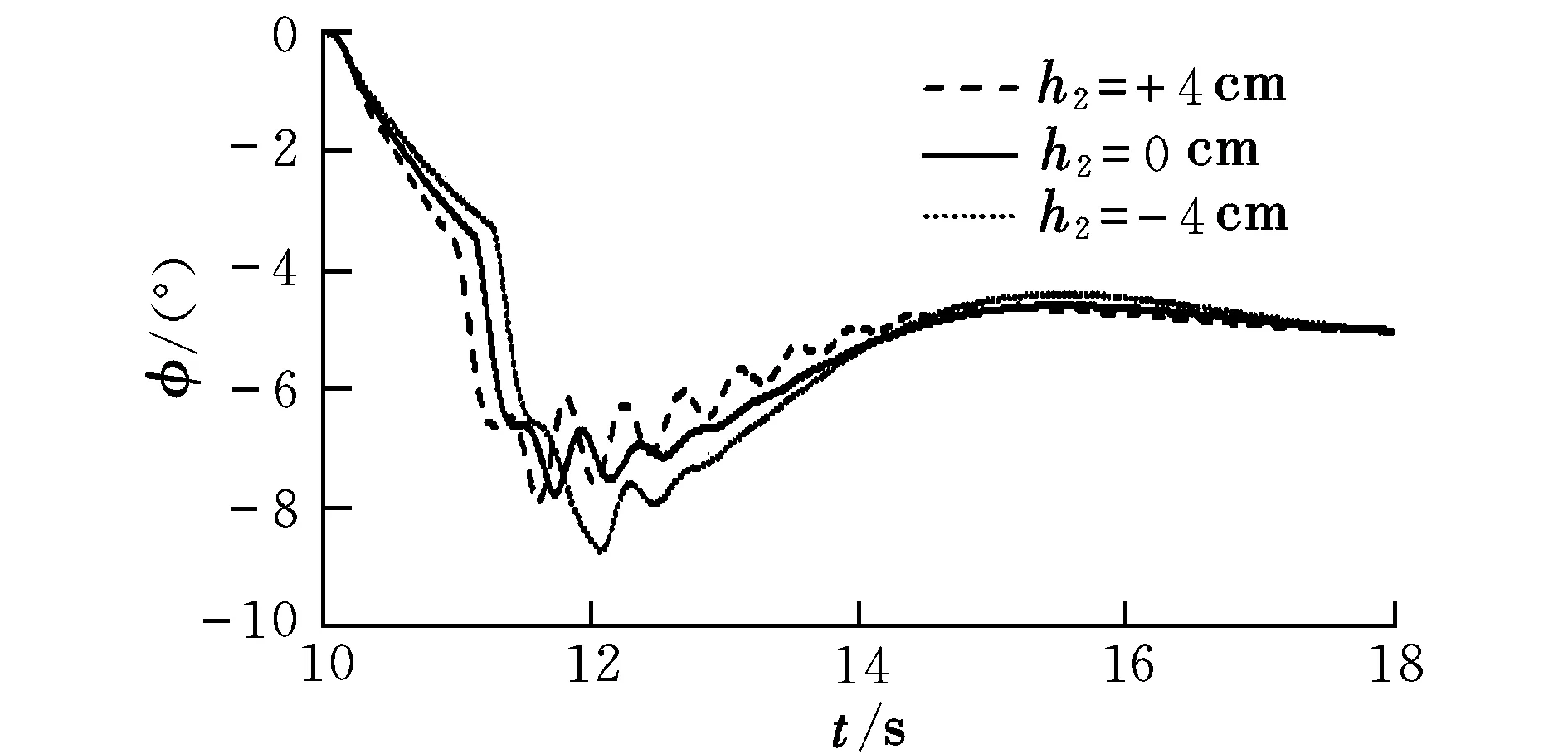
圖8 滾翼機滾轉角曲線Fig.8 Roll angle of cyclogyro

圖9 滾翼機偏航角速度曲線Fig.9 Yaw angular velocity of cyclogyro

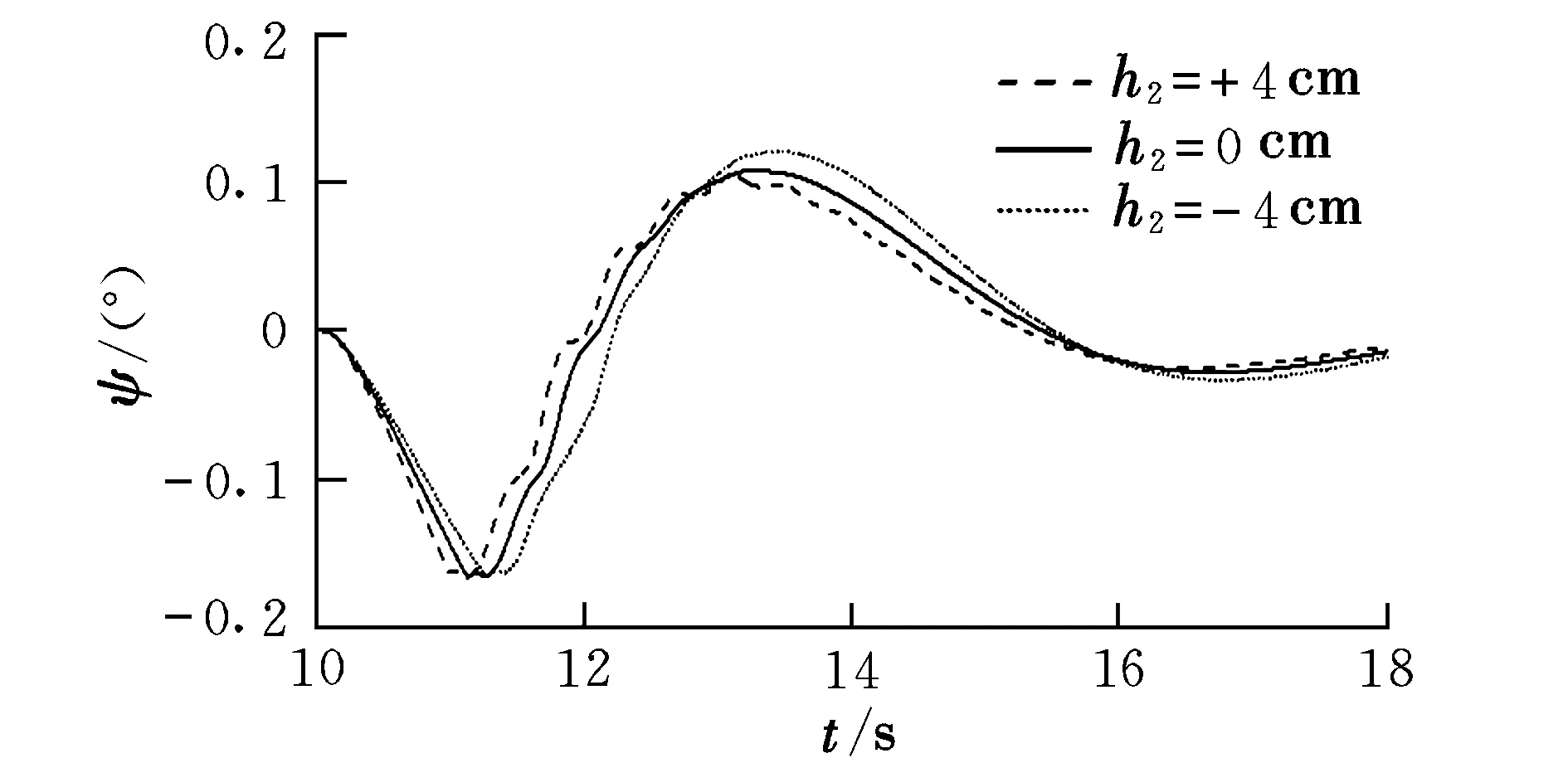
圖10 滾翼機偏航角曲線Fig.10 Yaw angle of cyclogyro

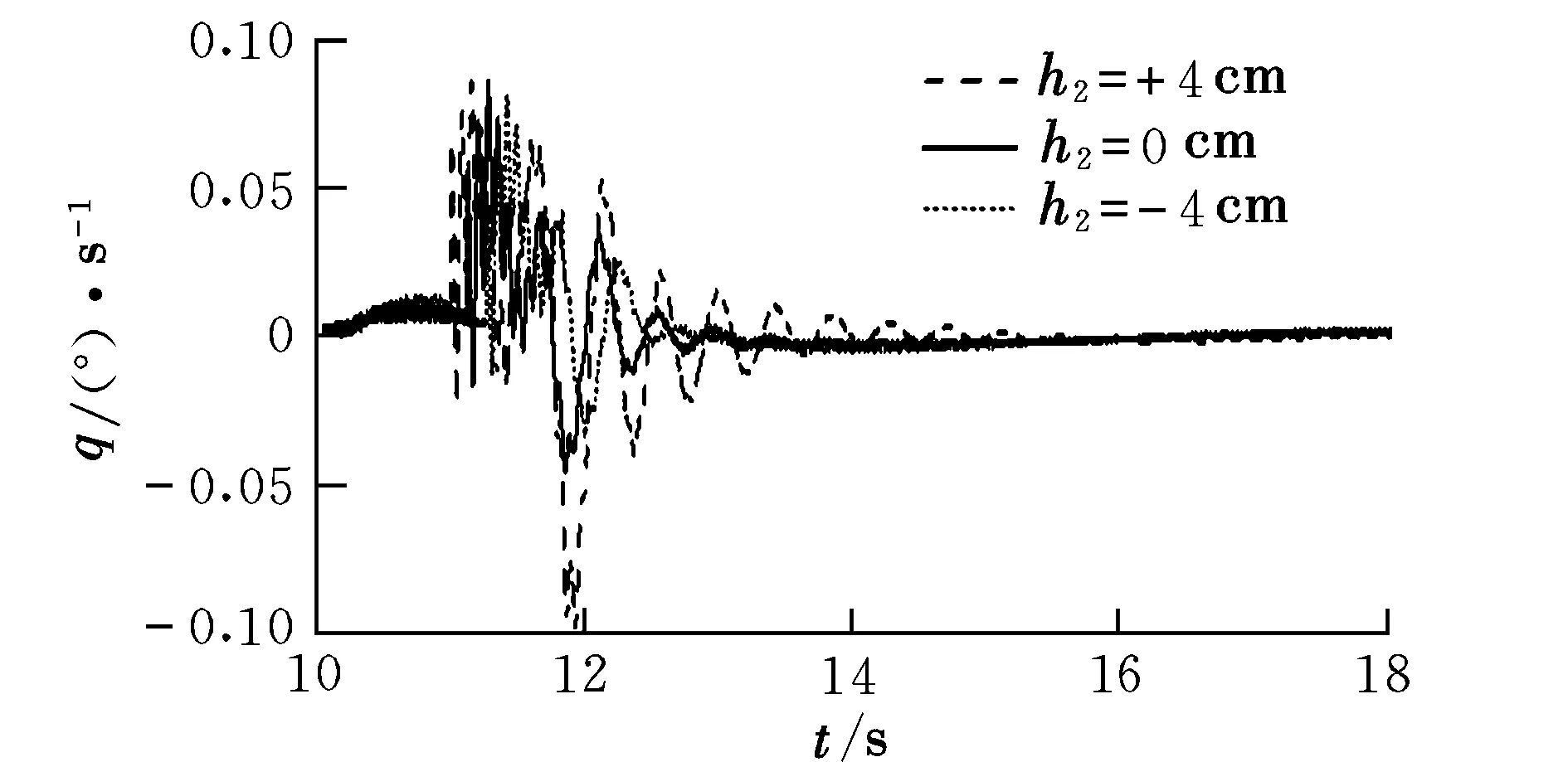
圖11 滾翼機俯仰角速度曲線Fig.11 Pitch angular velocity of cyclogyro

分析對比滾翼機滾轉過程中滾轉角、滾轉角速度的變化曲線(見圖7和圖8),可得到如下結論:

(1)h2=+4 cm時,飛行器滾轉角、滾轉角速度的響應速度最快，但曲線振蕩幅值大、頻率高,滾轉角超調量σ=58%,上升時間tr=0.85 s,峰值時間tp=1.60 s;(2)h2=0 cm時,飛行器滾轉角、滾轉角速度的響應速度居中,曲線振蕩幅值及頻率居中,σ=56%,tr=1.00 s,tp=1.72 s;(3)h2=-4 cm時,飛行器滾轉角、滾轉角速度的響應速度最慢，但曲線振蕩幅值小、頻率低,σ=75%,tr=1.14 s,tp=2.06 s。

對比3組數據可以發現,當h2>0時，系統的超調量較小，上升時間及峰值時間較短。

參數h2對滾翼機產生影響的原因為:擺線槳的轉動慣量為螺旋槳的45倍,其產生的陀螺力矩對于滾翼機具有顯著影響。影響過程為:當飛行器左滾時,擺線槳產生的陀螺力矩使滾翼機左偏航,因此滾翼機具有滾轉偏航耦合現象(見圖9、圖10);飛控系統將控制尾槳左偏以抵消該陀螺力矩,同時尾槳的水平分力會產生滾轉力矩Ft2h2,該滾轉力矩作用于滾轉控制過程中,將對滾轉控制產生影響。當h2>0時,該滾轉力矩方向與機體滾轉角速度方向相同,從而加速飛行器的滾轉。當h2=0時,該力矩大小為零,不會對機體滾轉產生影響。當h2<0時,該滾轉力矩方向與機體滾轉角速度方向相反,從而阻礙飛行器的滾轉。

滾翼機滾轉過程中俯仰角速度變化曲線如圖11所示。引起俯仰角速度變化的原因為:在滾轉過程中,滾翼機的高度將會產生變化;為了維持飛行高度,擺線槳及螺旋槳的升力將產生變化,最終引起俯仰角速度的變化。因此滾翼機具有高度俯仰耦合現象。

由此可知,三軸式布局滾翼機是一種存在復雜耦合關系的新型飛行器,保持其穩定性的難度高于其他類型無人機。仿真結果合理解釋了滾翼機在試飛過程中(見圖12)出現的三軸力矩強耦合現象。

圖12 滾翼機試飛場景Fig.12 Flight test scene of cyclogyro

4 結束語

本文針對三軸式布局滾翼機,建立了完整的動力學模型,首次通過仿真分析揭示了總體參數對滾翼機滾轉穩定性的影響。仿真結果能夠合理解釋飛行試驗中出現的三軸力矩耦合現象,并指出了改善其滾轉穩定性的參數設計方法。本文對今后此類滾翼機的設計研究具有一定的指導作用及技術價值。目前,尚未完全完成滾翼機三軸穩定性的研究,因而下一步亟需對偏航和俯仰穩定性進行探索,從而更好地改善三軸式滾翼機的飛行穩定性。

參考文獻：

[1] Curtis Boirum,Scott Post.Review of historic and modern cyclogyro design[R].AIAA-2009-5023,2009.

[2] Yu Hu,Kah Lim,Wen Hu.The research on the performance of cyclogyro[R].AIAA-2006-7704,2006.

[3] Moble Benedict,Mattia Mattaboni,Inderjit Chopra,et al.Aeroelastic analysis of a MAV-scale cycloidal rotor [R].AIAA-2010-2888,2010.

[4] 高浩,朱培申,高正紅.高等飛行動力學[M].北京:國防工業出版社,2004:1-6.

[5] 聶博文.微小型四旋翼無人直升機建模與控制方法研究[D].長沙:國防科學技術大學,2006.