支柱瓷絕緣子表面裂紋應力強度因子的有限元分析*

肖漢寧，彭蘇華，高朋召

(湖南大學 材料科學與工程學院, 湖南 長沙 410082)

近年來電站用高壓支柱瓷絕緣子斷裂事故時有發生，給電力系統正常運行及人身安全帶來危害.對大量事故原因進行分析，不難發現，瓷件斷裂與結構中存在的裂紋有關，而表面裂紋對瓷件強度的影響尤為突出.應力強度因子是判斷含裂紋構件斷裂和計算裂紋擴展速率的重要參量，而應用斷裂力學來解決工程實際問題，首先需要確定裂紋尖端的應力強度因子[1-2].

隨著計算機模擬技術的發展，裂紋仿真成為可能.在眾多仿真方法中，有限元法以其不受裂紋體幾何及載荷形式的限制而在斷裂力學中得到廣泛應用[3].通過有限元軟件ANSYS，ABAQUS等可計算裂紋尖端應力強度因子，計算的關鍵在于如何構建能夠反映裂紋尖端奇異應力場的裂紋模型.三維裂紋模型的建立一般有兩種方法：逐節點直接建模法和實體建模法.前者雖為多數人采用，但工作繁瑣且容易出錯，不適合復雜結構[4].

本文針對支柱瓷絕緣子結構中常見的表面裂紋，采用實體建模法，首先對整體結構和裂紋部分分別建模，然后運用布爾運算將其分離，再對裂紋部分采用特殊的網格劃分方式進行劃分，最后通過施加邊界條件和載荷來計算不同尺寸、位置的裂紋尖端應力強度因子.

1 有限元法求解應力強度因子基本理論

基于三維有限單元法的裂紋尖端應力強度因子計算方法主要有1/4節點位移法和三維J積分法[5]，其中J積分法計算應力強度因子的過程較為繁雜，不便于多次重復求解，本文選擇1/4節點法計算裂紋尖端應力強度因子K值.根據線彈性斷裂力學理論[6-8]，裂紋尖端的位移場可表示為：

(1)

(2)

ut=0．

(3)

式中：n和t分別為裂紋前沿的法線方向和切線方向；z為垂直于裂紋平面方向(見圖1)；μ為材料剪切模量.

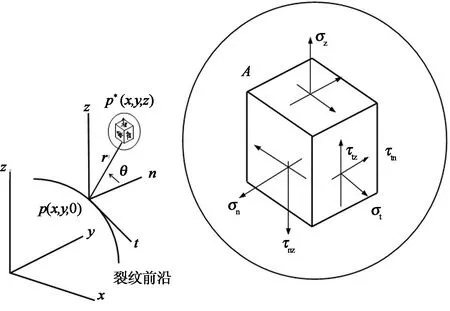
圖1 曲線裂紋前緣坐標系

根據式(2)，若裂紋表面上(θ=180°)某一點的垂直于裂紋平面的位移已知，那么應力強度因子

(4)

將從有限單元法求出的1/4點位移uz(1/4)代入式(4)得

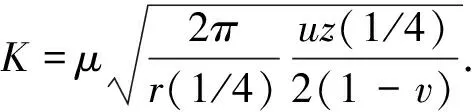
(5)

2 有限元模型的構建及計算求解

支柱瓷絕緣子一般由鑄鐵法蘭、水泥膠合劑、瓷體三部分膠裝而成，分析時假設兩種材料之間完全粘牢，即兩種材料接觸界面不存在相對滑動.組成絕緣子的各材料特性參數值如表1所示，文中所使用的絕緣子主要尺寸參數如表2所示.

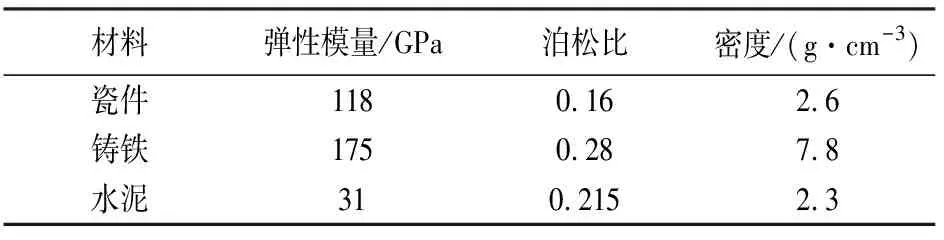
表1 瓷絕緣子組成材料的性能參數

表2 瓷絕緣子主要尺寸參數

實際工程中，裂紋是不規則的，半橢圓裂紋是表面裂紋的一種理想化形式，是仿真計算中常用的一種模型[9].本文將表面裂紋簡化為半橢圓形狀處理，裂紋位于支柱表面垂直于軸向，彎曲載荷作用于絕緣子上法蘭處，平行于裂紋面.支柱瓷絕緣子的幾何模型和裂紋橫截面示意如圖2，其中d1=2R；a為橢圓短半軸，即裂紋深度；b為橢圓長半軸，2b約等于裂紋長度.

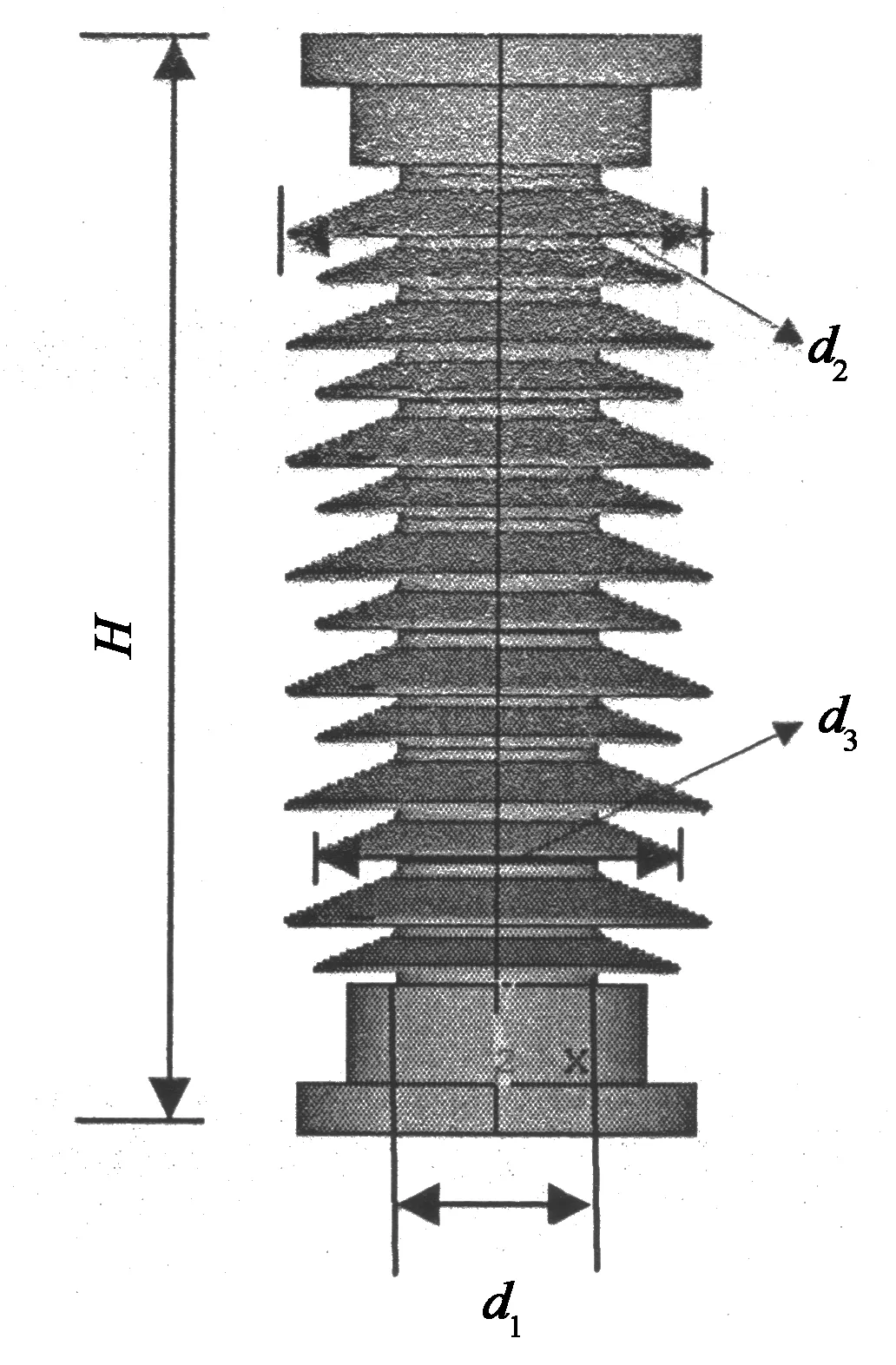
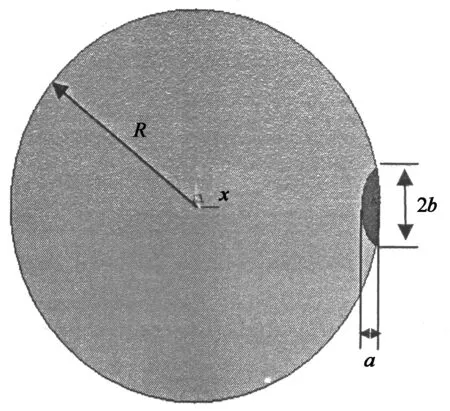
圖2 瓷絕緣子幾何模型及裂紋橫截面說明

研究中采用“自上向下”的實體建模方法，該方法關鍵在于對裂紋部分進行特殊的網格劃分.由于

裂紋尖端的應力和應變是奇異的，因此在進行有限元建模或單元網格劃分時，必須先在裂紋尖端位置定義應變奇異點，而常規單元的位移模式不能反映尖端位移處的奇異性.Barsoum等[10]通過把裂紋尖端附近二階單元的中間節點沿裂紋尖端方向移至靠近裂尖1/4分點處(如圖3)，較準確地反映了裂尖附近應力場的奇異性.

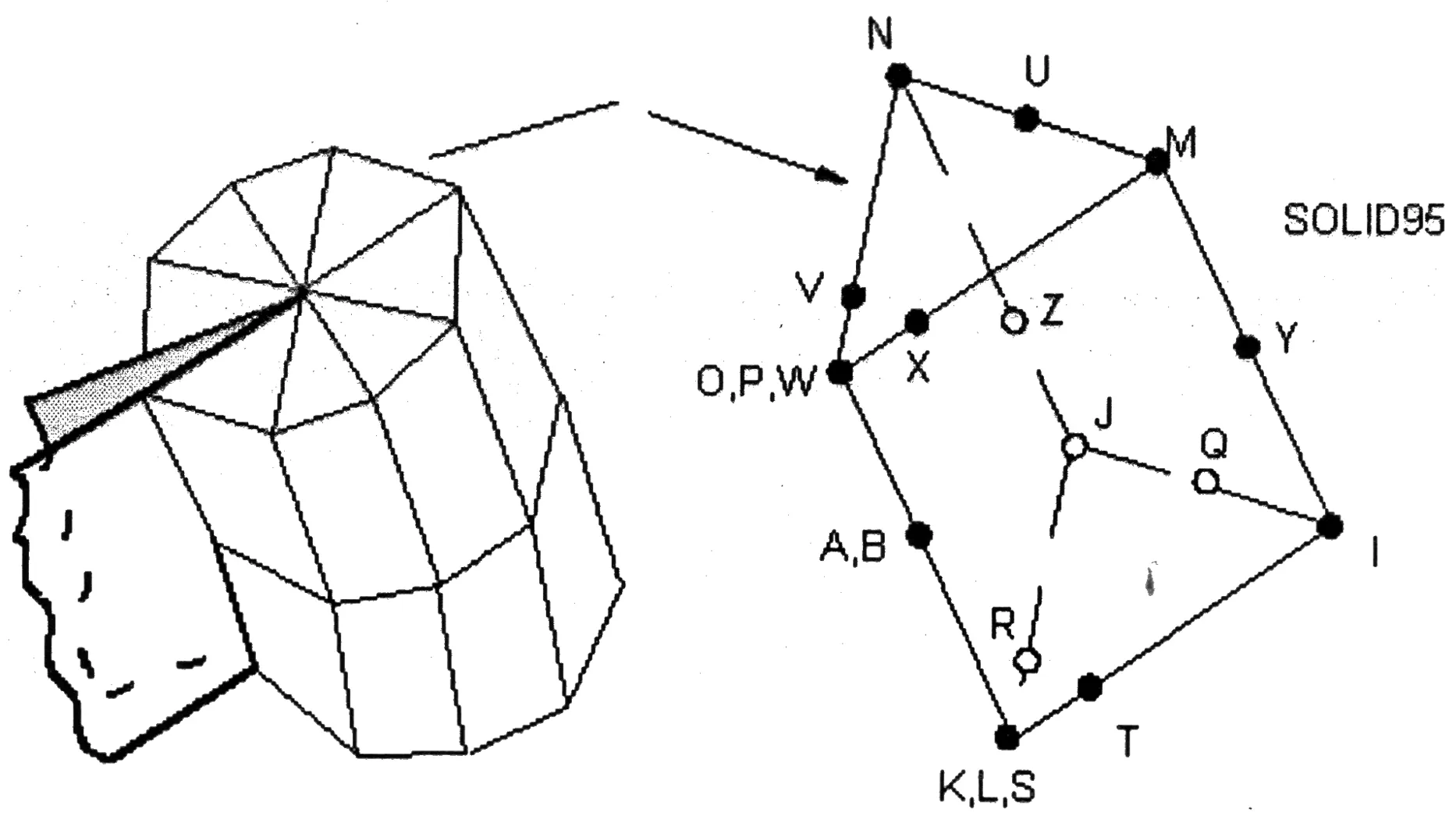
圖3 裂紋前緣奇異單元及尖端附近網格構造

分析中，裂紋前緣采用20節點solid 186單元的棱柱退化形式模擬其奇異性，劃分網格時首先是采用MESH200單元，通過在裂紋尖端設置奇異點來生成二維的奇異單元(圖4(a))，然后將所生成的面網格沿裂紋深度方向通過體掃掠劃分生成三維單元(圖4(b)).對非裂紋區采用4節點solid 285單元進行網格劃分，最后瓷絕緣子整體有限元模型如圖4(c)所示.為了獲得理想計算結果，圍繞裂紋尖端單元的第一行單元半徑設為1/8裂紋深度或更小，單元角度在15～30°之間.

圖4 裂紋體模型的生成及瓷絕緣子有限元模型

支柱瓷絕緣子的有限元模型建立后，對絕緣子底端施加位移約束，頂部施加一垂直軸向的載荷Fx，然后進行結構靜力學計算.在ANSYS中，通過通用后處理器POST1的KCALC命令[11]，采用平面應變位移外推法計算應力強度因子，使用此命令前，需要定義描述裂紋尖端的局部坐標系和計算路徑，坐標系的X軸平行于裂紋面且垂直裂紋前緣，Y軸垂直于裂紋面.沿裂紋面的路徑以裂紋尖端為第1點，另外4個附加點取距離尖端最近的節點，每個裂紋面各2個，如圖5所示.

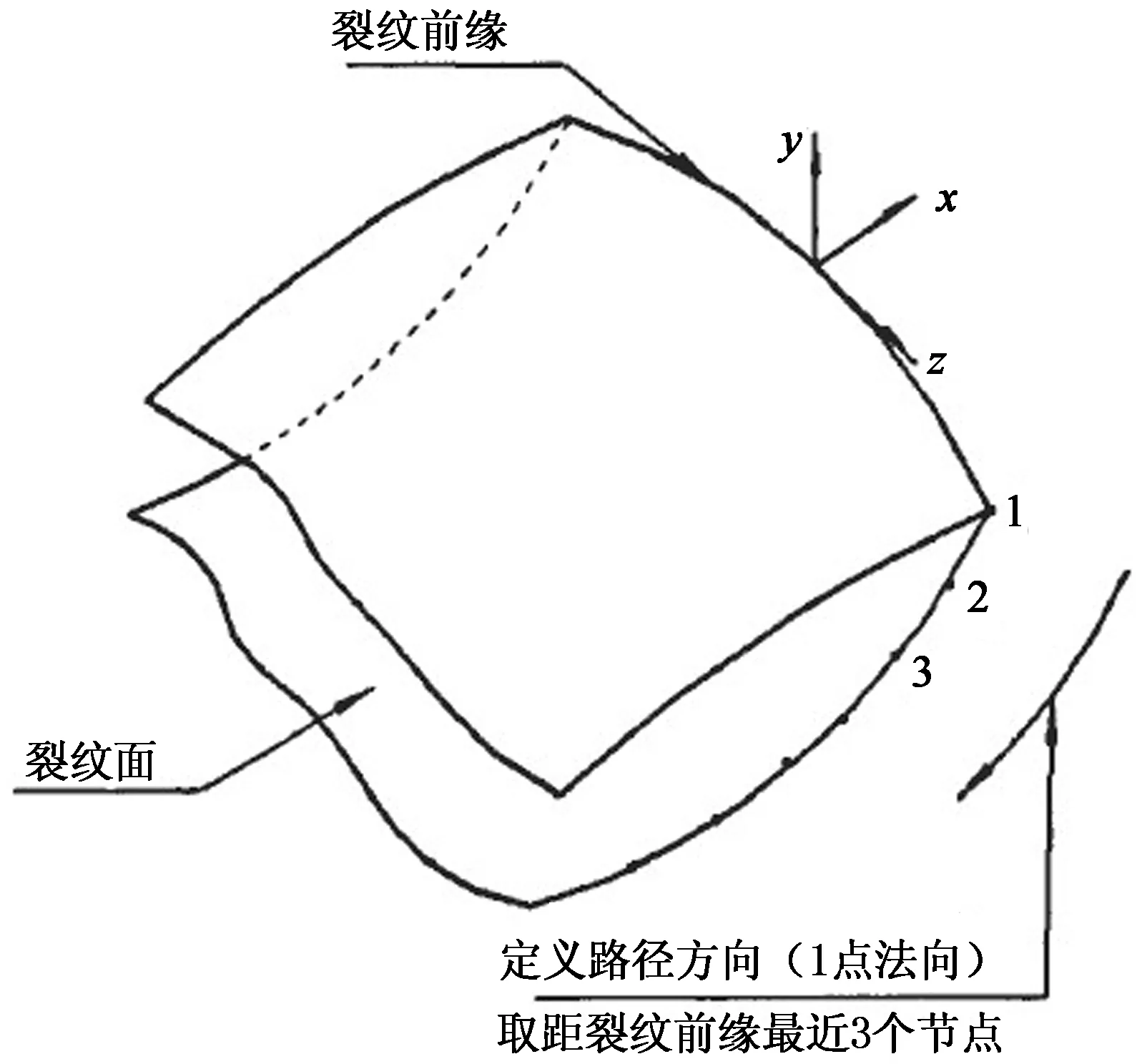
圖5 裂紋前緣局部坐標系及路徑定義

3 計算結果及分析

由于支柱瓷絕緣子受彎曲力作用，彎曲正應力方向與裂紋面垂直，故I型裂紋應力強度因子占主導地位，因而本文主要分析I型裂紋尖端應力場強度因子的變化規律，即裂紋形狀比(a/b)、裂紋深度a、裂紋所處支柱位置及加載載荷變化對應力強度因子的影響.計算結果表明，裂紋前緣不同位置處的K值有所不同，分布呈現規律性，選取裂紋前緣各點中的兩個表面點和一個最深點作為重點來考察應力強度因子在裂紋前沿的分布情況.

3.1 裂紋位置對 KI 的影響

形狀、尺寸相同但在構件中位置不同的裂紋，其尖端應力強度因子不同.為此，本文設計的單條半橢圓表面裂紋分別位于瓷絕緣子支柱表面的上、中、下3處(y=855 mm，509 mm，107 mm)，其中上、下兩處分別靠近上、下法蘭口，裂紋形狀比a/b= 0.5，裂紋深度a=1 mm，載荷Fx=16 kN，其他條件相同，分別計算三種情況下裂紋表面點及最深點的KI值，結果如圖6所示.圖中橫坐標軸“0”表示裂紋最深點，“1”和“-1”表示裂紋兩個表面點.

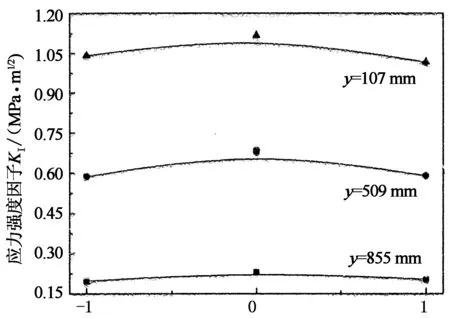
裂紋前緣相對位置

由圖6可知，三種情況下裂紋前緣的KI值均為表面點最小，最深點最大.各點KI值關于最深點呈對稱分布，且表面點與最深點KI差值隨著裂紋向下移動而呈增大趨勢.支柱表面相同形狀和尺寸的裂紋從絕緣子頂部到底端，應力強度因子逐漸增大.其中下法蘭口附近裂紋KI值最大達到1.117 MPa·m1/2，當載荷增大后，支柱下端的裂紋應力強度因子最先達到斷裂韌性值，這與統計數據中支柱瓷絕緣子斷裂部位95%以上位于法蘭口內3 cm到第一瓷裙之間[12-14]相吻合.亦即支柱絕緣子的最小臨界裂紋應位于支柱下端法蘭口附近，因而此區域也應成為支柱瓷絕緣子無損探傷的重點區域.分析認為，彎曲受力情況下，支柱瓷絕緣子最底端傘裙根部與下法蘭口之間為受力最大處(如圖7)，裂紋如果位于這些區域或附近，更容易造成支柱絕緣子的破壞.

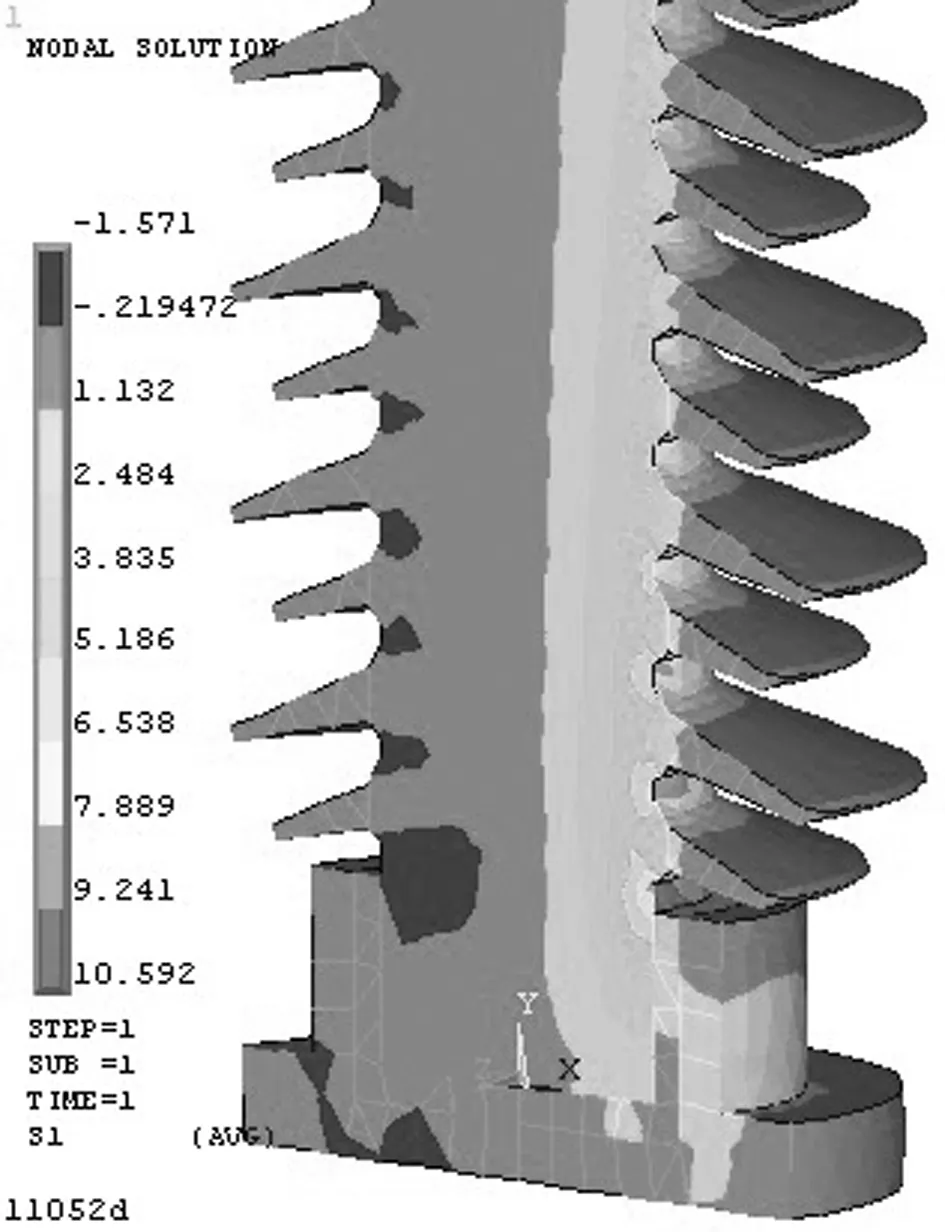
圖7 絕緣子無缺陷時第一主應力S1分布(Fx=6KN)

鑒于上述分析，下文分析中主要對支柱絕緣子下法蘭口附近(y=107 mm)的裂紋進行系統研究.

3.2 裂紋形狀比(a/b)對KI 的影響

裂紋深度a保持1 mm不變，載荷16 kN，此時KI隨a/b的變化規律如圖8所示.

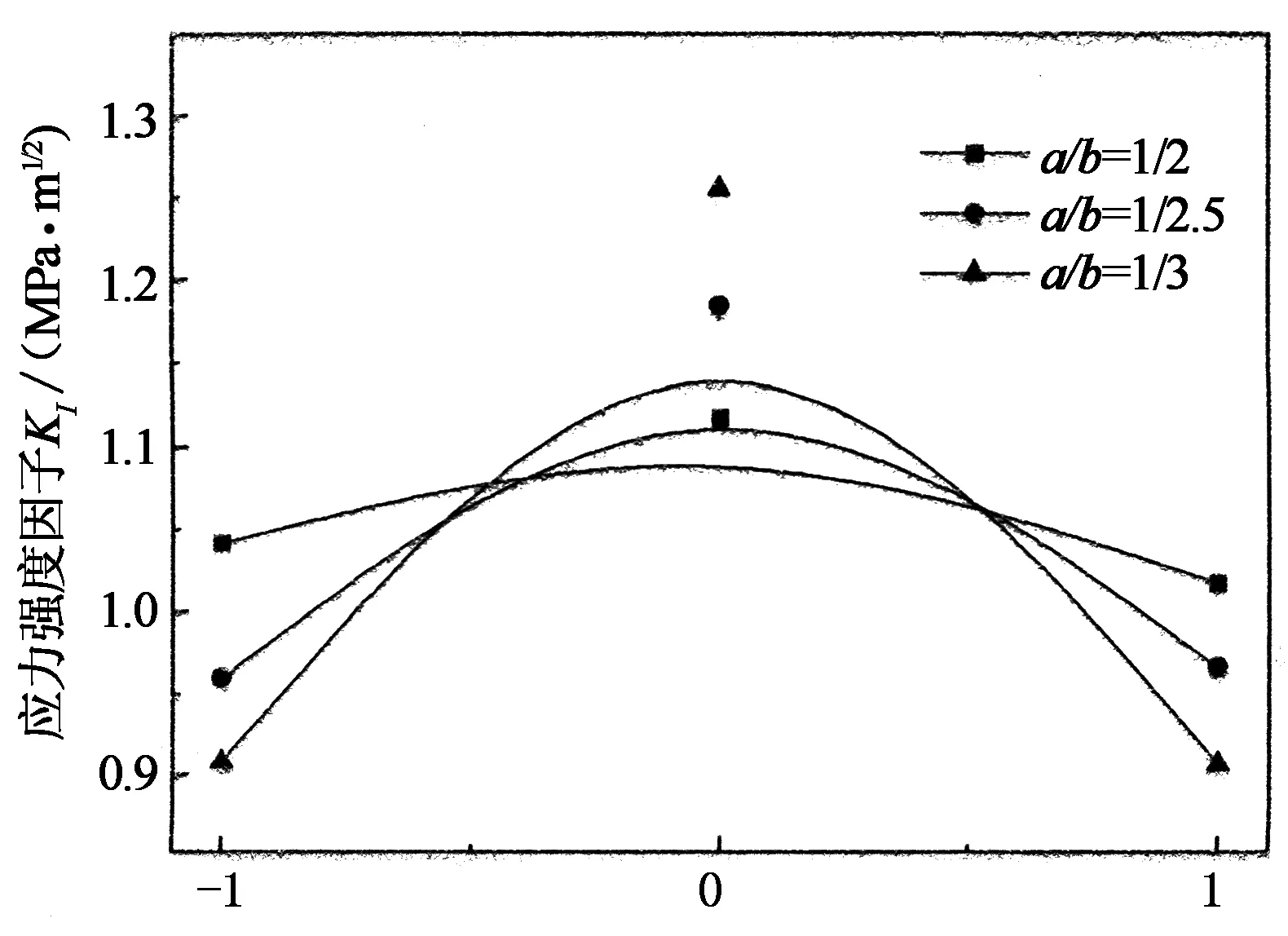
裂紋前緣相對位置

由圖8不難看出，裂紋前沿橢圓率(a/b)較小的情況下，裂紋前緣中心點(最深處)有最大的KI值，表面點KI值最小.隨著裂紋前沿趨向平直，中心點的應力強度因子逐漸增大，當a/b=1/3時，KI值達到1.255 MPa·m1/2，瓷件更容易破壞，而表面兩點KI值逐漸減小，故中心點與表面點的差值也逐漸增大.

3.3 裂紋深度對KI的影響

當a/b= 0.5，Fx=16 kN，KI隨裂紋深度的變化規律如圖9所示.

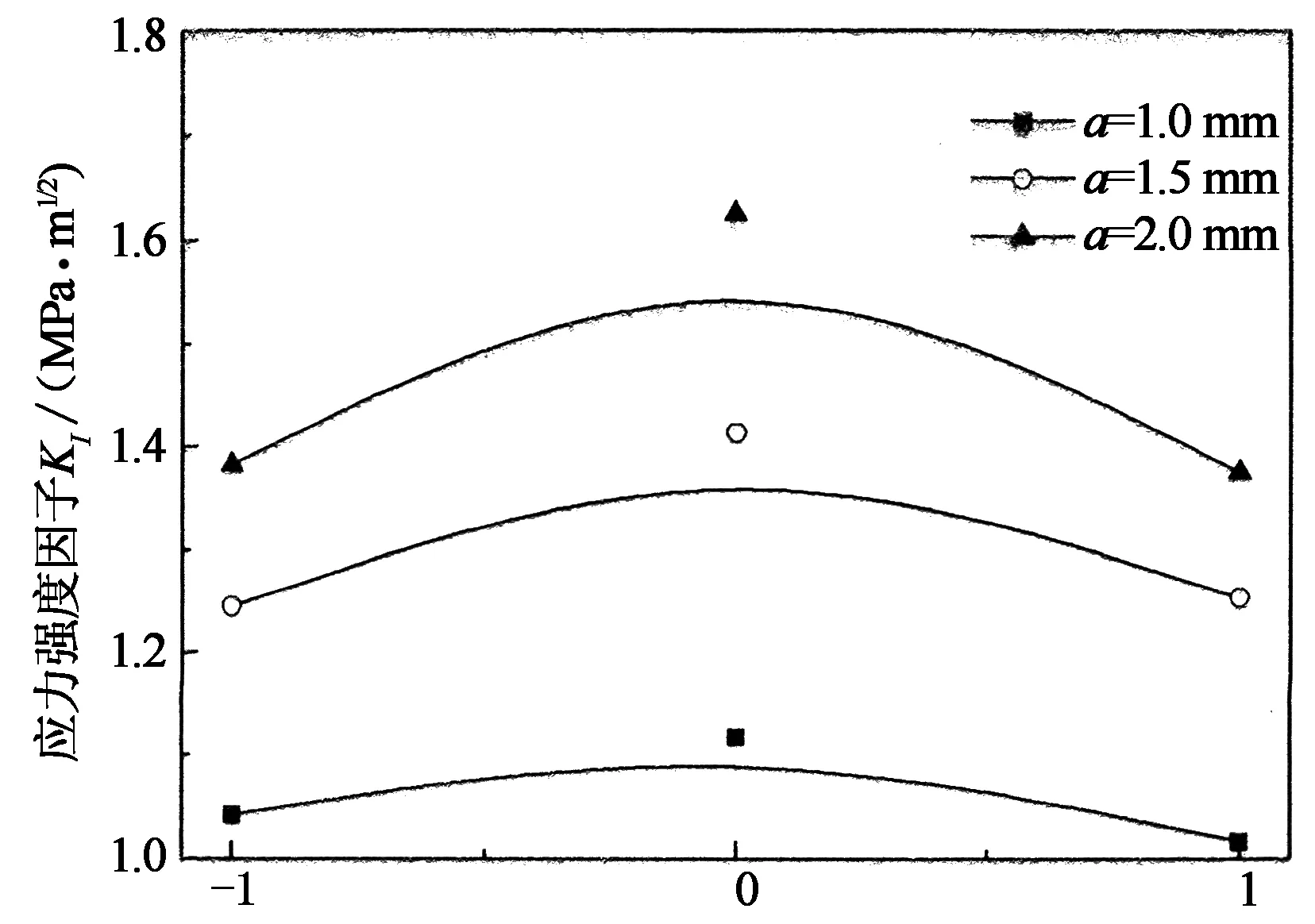
裂紋前緣相對位置

由圖9可知，其它參數保持不變時，隨著裂紋深度的增大，裂紋前緣各點的KI也逐漸增大，且表面點與最深點差值有增大趨勢.當a=1.5mm時，KI=1.413 MPa·m1/2，a增大到2 mm時，KI增加到1.625 MPa·m1/2，當a繼續增大則隨著KI逐漸逼近KI(設為2 MPa·m1/2)，預計絕緣子支柱將產生破壞性后果.

3.4 加載載荷對KI的影響

當a=1 mm，b=2 mm時，KI隨載荷變化情況如圖10所示.結果表明，裂紋前沿各點應力強度因子隨載荷變化呈線性關系，隨著載荷的增加而增大，且最深點KI隨載荷的增大趨勢要略高于表面兩點.由脆性材料的斷裂力學理論可知，當載荷增加到一定程度，KI達到材料的斷裂韌性時，裂紋失穩擴張，斷裂迅速發生.反之，在額定載荷下，裂紋位置、形狀一定時，通過有限元計算反推出臨界裂紋尺寸，可為支柱瓷絕緣子無損檢測所需靈敏度提供參考依據.

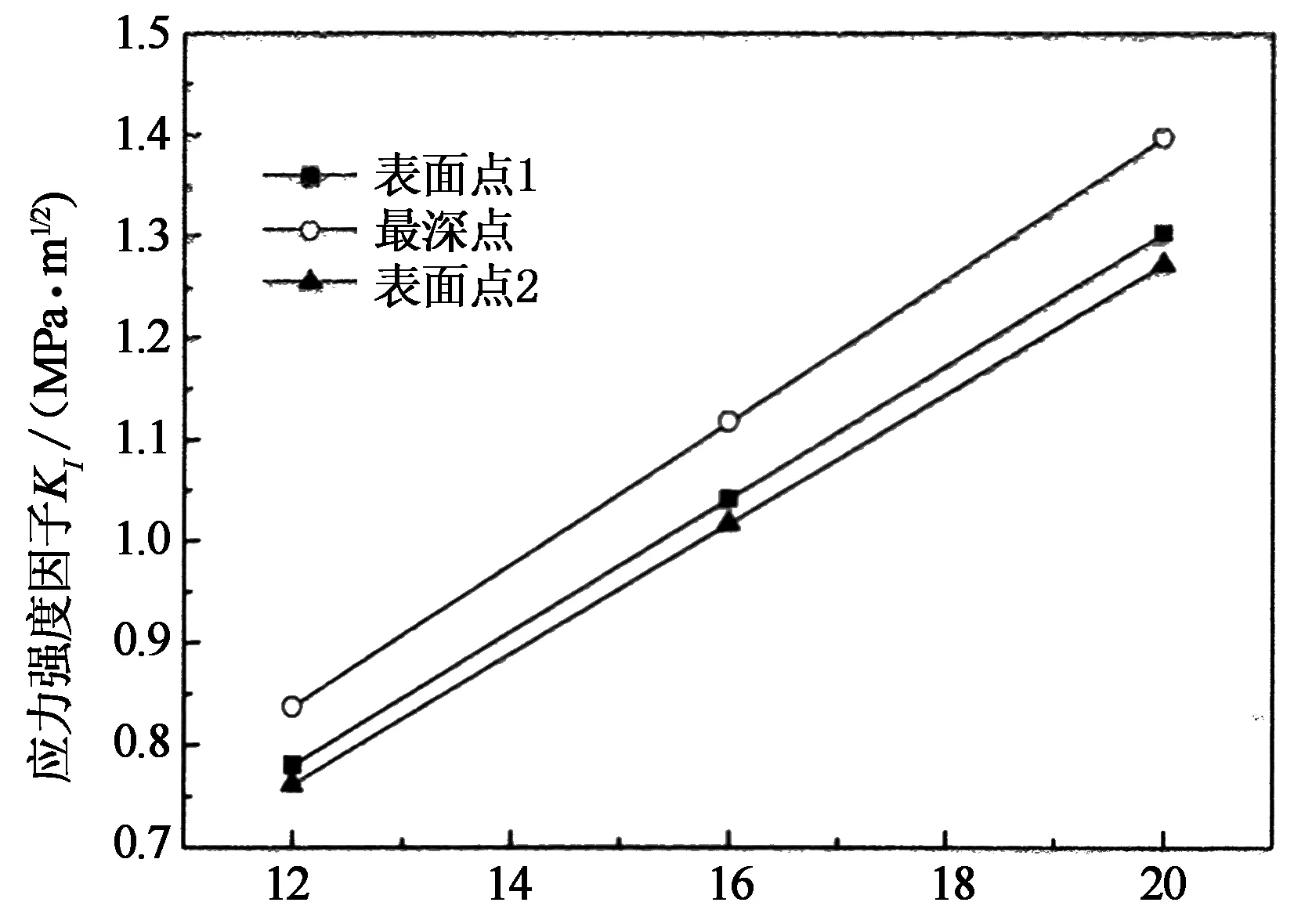
載荷x/kN

4 結 論

本文以支柱瓷絕緣子的彎曲破壞試驗為原型，計算了多種情況下支柱表面半橢圓裂紋前沿各點的應力強度因子KI，得出主要結論如下：

1) 利用實體建模方法，通過在表面半橢圓裂紋前緣設置生成三維奇異單元，建立了含裂紋支柱瓷絕緣子彎曲破壞的有限元模型；

2) 采用1/4節點法計算不同尺寸、形狀的裂紋尖端應力強度因子，結果表明裂紋前沿橢圓形狀比較小的情況下，最深處具有最大應力強度因子，裂紋前緣各點的KI呈對稱分布，且KI隨裂紋深度的增大而增大，隨橢圓率的增大而減小；

3) 支柱瓷絕緣子不同位置處的表面裂紋(形狀、尺寸參數相同)對支柱應力分布的影響不同，尤其是靠近底端法蘭口的表面裂紋缺陷，進一步加劇了缺陷附近的應力集中效應.通過對該處最小臨界裂紋尺寸的分析，可確定絕緣子缺陷無損檢測所需的靈敏度.

[1]瞿偉廉, 魯麗君, 李明. 工程結構三維疲勞裂紋最大應力強度因子計算[J]. 地震工程與工程振動, 2007, 27(6): 58-63.

QU Wei-lian, LU Li-jun, LI Ming. Calculation of the maximum stress intensity factor of 3-D fatigue crack in engineering structures[J]. Journal of Earthquake Engineering and Engineering Vibration, 2007, 27(6): 58-63. (In Chinese)

[2]馬艷. 結構表面裂紋應力強度因子計算方法研究[D]. 大連：大連理工大學, 2007.

MA Yan. Study on method for calculating SIF of structural surface crack[D]. Dalian: Dalian University of Technology, 2007. (In Chinese)

[3]王永偉, 林哲. 表面裂紋的三維模擬及應力強度因子計算[J]. 中國海洋平臺, 2006, 21(3): 23-26.

WANG Yong-wei, LIN Zhe. 3-D Simulation and stress intensity factors calculation of surface crack[J]. China Offshore Platform, 2006, 21(3): 23-26. (In Chinese)

[4]瞿偉廉, 魯麗君, 李明. 帶三維穿透裂紋結構的有限元實體建模方法[J]. 武漢理工大學學報, 2008, 30(1): 87-90.

QU Wei-lian, LU Li-jun, LI Ming. Solid modeling method for structure with 3-D straight through crack[J]. Journal of Wuhan University of Technology, 2008, 30(1): 87-90. (In Chinese)

[5]LIN X B, SMITH R A. Stress intensity factors for corner cracks emanating from fastener holes under tension[J]. Engineering Fracture Mechanics, 1999, 62(6): 535-553.

[6]IRWIN G R. Crack-extension force for a part-through crack in a plate[J]. Journal of Applied Mechanics, 1962, 29: 651-654.

[7]KASSIR M K, SIH G C. Three-dimensional stress distribution around an elliptical crack under arbitrary loadings(Three-dimensional stresses near border of discontinuity plane under arbitrary loading, obtaining solution for uniform shear applied to surface of crack)[J]. ASME, Transactions, Series E-Journal of Applied Mechanics, 1966, 33: 601-611.

[8]SMITH F W, KOBAYASHI A S, EMERY A F. Stress intensity factors for penny-shaped cracks: part 1—infinite solid[J]. Journal of Applied Mechanics, 1967, 34: 947-952.

[9]陳曉明, 矯桂瓊, 崔振源. 復合型斷裂準則在半橢圓表面裂紋問題中的應用[J]. 西北工業大學學報, 1986, 4(4): 385-393.

CHEN Xiao-ming, XU Gui-qiong, CUI Zhen-yuan, Application of combined-mode fracture criteria to semi-elliptical surface crack problems[J]. Journal of Northwestern Polytechnical University, 1986, 4(4): 385-393. (In Chinese)

[10]FEHL B D, TRUMAN K Z. An evaluation of fracture mechanics quarter-point displacement techniques used for computing stress intensity factors[J]. Engineering Structures, 1999, 21(5): 406-415.

[11]張朝暉.ANSYS12.0結構分析工程應用實例解析[M].3版.北京:機械工業出版社,2010.

ZHANG Chao-hui. ANSYS12.0 structural analysis instances for engineering application[M]. The 3rd edition. Beijing: China Machine Press, 2010. (In Chinese)

[12]王云昌. 支柱瓷絕緣子的超聲波檢測[J]. 江西電力, 2007, 31(3): 1-2.

WANG Yun-chang. The ultrasonic inspection for porcelain strut insulators[J]. Jiangxi Electric Power, 2007, 31(3): 1-2. (In Chinese)

[13]王維東, 劉勇. 支柱絕緣子及瓷套超聲波探傷工藝方法研究[J]. 無損檢測, 2006, 28(9): 460-462.

WANG Wei-dong, LIU Yong. Research on ultrasonic inspection technique of pillar insulators and porcelain cover[J]. Nondestructive Testing, 2006, 28(9): 460-462. (In Chinese)

[14]印華, 王謙, 王勇,等. 支柱瓷絕緣子斷裂原因分析及檢測方法[J]. 電力安全技術, 2007, 9(12): 47-48.

YIN Hua, WANG Qian, WANG Yong,etal. The failure analysis and detection methods for porcelain strut insulators[J]. Electric Safety Technology, 2007, 9(12): 47-48. (In Chinese)