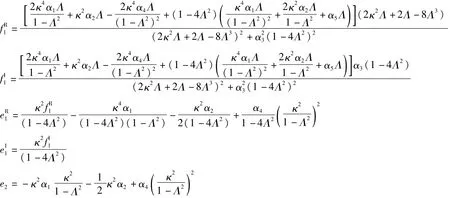考慮材料非線性時壓電發電懸臂梁的主共振響應分析

郭抗抗， 曹樹謙

（1．天津大學 機械工程學院力學系，天津 300072；2．天津市非線性動力學與混沌控制重點實驗室，天津 300072）

近年來，微機電系統（MEMS）的快速發展促使微電源技術的興起。傳統化學電池在使用、壽命及環保等方面的限制促使人們探索如何利用環境能量進行發電。Williams［1］首次提出收集環境中的振動能轉化為電能，而微電子設備低功耗的特點使得利用環境振動自供能成為可能。目前振動能量采集器主要有電磁式［2］、靜電式［3］和壓電式。其中利用壓電材料正效應的壓電式發電系統優勢明顯備受關注［4］。其結構簡單、綠色環保、能量密度高、無電磁干擾、壽命長，可直接輸出較高電壓，且易于加工和實現微型化、集成化［5］。d31工作模式下的雙晶或單晶懸臂梁是最常用的結構形式［6］。目前國內外針對壓電懸臂梁發電特性已開展了大量研究。Roundy等［7］利用等效電路法對端部有集中質量的壓電懸臂梁進行了建模分析，并通過實驗給出了輸出電壓、功率與負載電阻的關系；Johnson等［8］則根據熱動力平衡方法分析了不同激勵下壓電梁的結構參數對電能輸出的影響；Sodano等［9］針對無附加質量的壓電懸臂梁，建立了機電耦合動力學和電學模型，并利用數值方法和實驗方法對理論模型進行了驗證；DuToit［10］則對帶集中質量的懸臂梁進行了分布式建模分析并通過實驗予以驗證；Erturk等［11］根據彈性理論和Galerkin方法分別對串、并聯雙晶壓電懸臂梁進行了理論建模并給出實驗驗證。在國內，闞君武等［12］建立了單、雙晶壓電梁發電能力的仿真分析模型，研究了結構參數對其發電能力的影響規律；袁江波等［13］對懸臂梁壓電振子進行了有限元分析，并對其發電性能進行了實驗研究；單小彪等［14］通過數值模擬和有限元仿真研究了截面形狀對懸臂梁雙晶壓電振子發電能力的影響；賀學鋒等［15］考慮逆壓電效應和梁集中質量的影響，給出系統的輸出電壓表達式并通過實驗驗證其準確性。

然而上述文獻中所有壓電材料均假設為線性材料。事實上，非線性是壓電材料的本質特征，即使在低場下也有明顯的非線性現象［16］，而在壓電發電研究中，只有少數文獻考慮到壓電材料非線性。Stanton等［17－18］考慮壓電材料三次非線性本構關系，通過理論建模分析了壓電懸臂梁的發電特性，結論表明在較大激勵振幅下，線性結果與實驗結果相差較大，指出線性結果的局限性。Abdelkefi等［19］考慮材料二次非線性本構關系，建立參數激勵下的壓電懸臂梁模型并進行了理論分析和數值模擬，同樣指出對壓電發電系統非線性建模的必要性。

本文以帶集中質量的單晶懸臂梁壓電發電系統為研究對象，考慮壓電材料的二次非線性本構關系，利用廣義Hamilton原理及Rayleigh－Ritz法建立其機電耦合模型；隨后利用多尺度法求解系統主共振二次近似響應，分析壓電材料非線性、外激勵參數及負載電阻對系統響應的影響；最后通過數值分析驗證了解析解的正確性。

1 壓電懸臂梁的機電耦合模型

圖1所示為基礎激勵下有附加質量的單晶懸臂梁壓電振子在d31工作模式下的振動示意圖。梁長為L，梁厚為t0，其中上層為壓電層（厚度為tp），下層為彈性結構層（厚度為ts），極化方向（P方向）沿3方向，x表示軸向坐標（沿1方向），y表示縱向坐標（沿3方向）。

1.1 材料的本構關系

對于彈性金屬梁結構而言，其應力－應變具有如下線性關系：

式中：cs11為彈性結構層的剛度系數，T1及S1表示沿1方向的應力、應變。

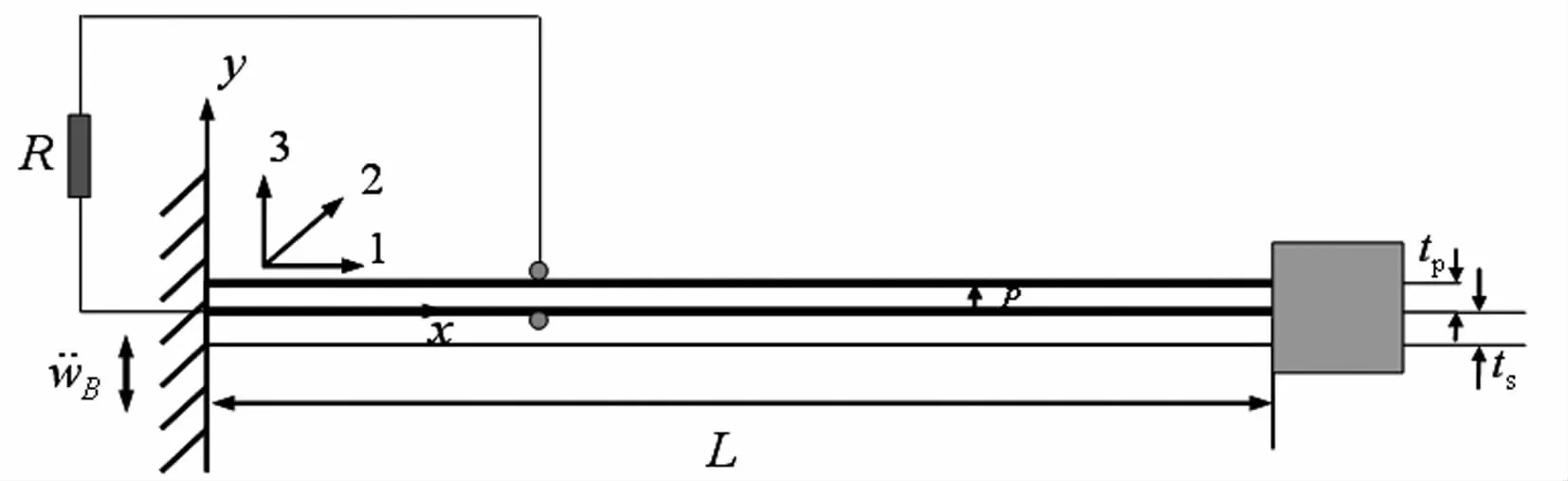
圖1 懸臂式壓電發電系統模型Fig．1 The vibrating model of piezoelectric cantilever with base excitation

考慮非線性壓電效應，壓電材料的非線性本構關系［20－21］可以表示為：

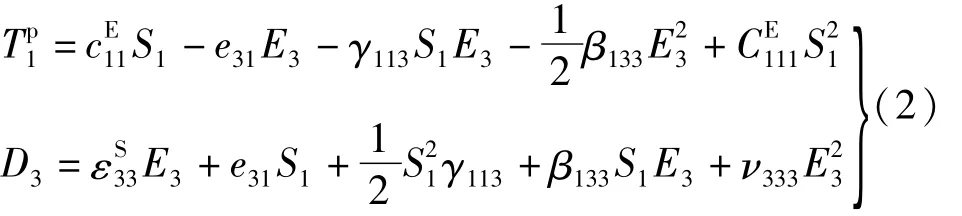
式中：E3和D3表示沿3方向的電場強度和電位移；cE11為壓電層的剛度系數；e31為壓電系數；εS33為介電常數；γ113為電致彈性系數；β133為電致伸縮系數；CE111為二次非線性剛度系數；ν333為二次非線性介電常數。

1.2 壓電梁機電耦合模型

基礎激勵下，壓電懸臂梁存在機械能和電能的轉換，利用機電耦合系統的廣義Hamilton變分原理［10］

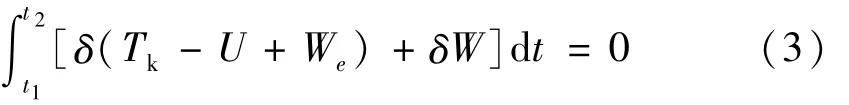
式中：Tk為系統動能；U為系統勢能；We為壓電陶瓷的電能；δW為外力做功的變分。分別表示如下：

式中：ρ表示材料密度；V表示體積；下標s和p分別為對應梁的彈性金屬層和壓電層；u（x，t）為梁的橫向相對位移；m0為懸臂梁端部集中質量；φ表示標量電勢；q表示電荷量。

為了表示基礎激勵下懸臂梁產生的慣性載荷，假設梁沿軸向均勻，單位長度質量用m表示，從而將慣性載荷表示是有

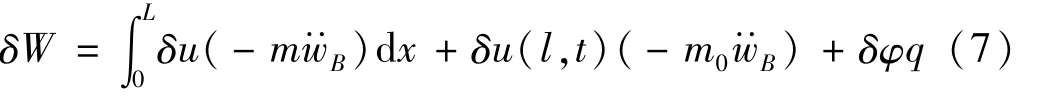
考慮梁的一階模態，并將壓電元件上下表面兩金屬電極看作一個電極對，應用 Rayleigh-Ritz法，Euler-Bernoulli梁理論及壓電元件恒定電場假設如下：

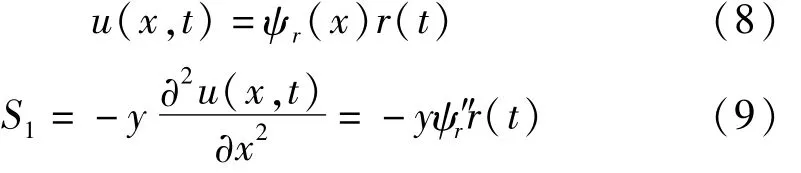
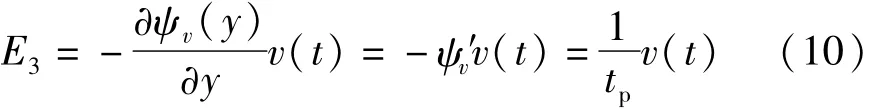
式中：ψr（x）表示懸臂梁的一階彎曲模態振型函數；r（t）表示梁橫向振動位移模態坐標；ψv（x）表示電勢分布函數；v（t）表示廣義電壓模態坐標。

對于帶有集中質量的懸臂梁，其一階模態振型函數為

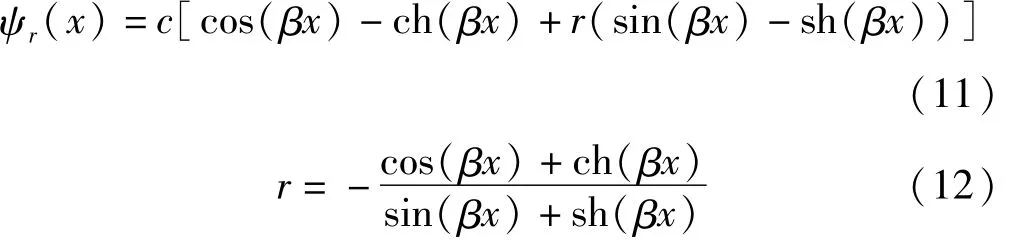
式中：β值及待定常數因子c可根據梁的邊界條件確定。

對于自由端附加集中質量的懸臂梁，其邊界條件為

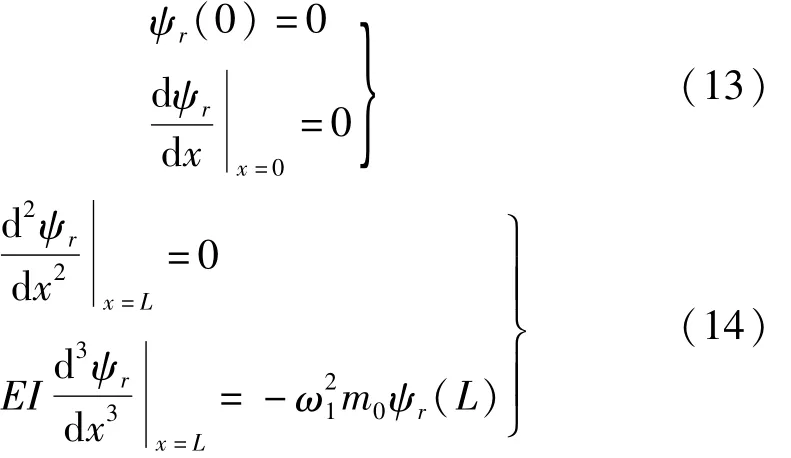
式中：EI為懸臂梁的彎曲剛度，ω1為懸臂梁一階固有頻率。

將式（8）～式（10）及式（1）、式（2）代入式（4）～式（7），并將重寫后的式（4）～式（7）代入式（3）可得如下兩個方程：

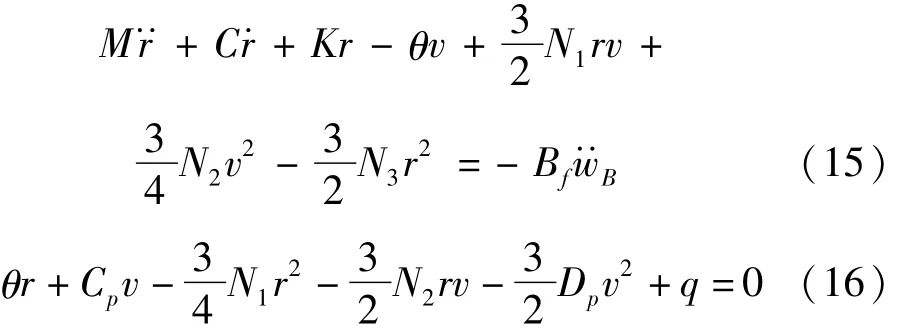
式中：M和K分別是層合梁振子的模態質量和模態剛度，表示如下：

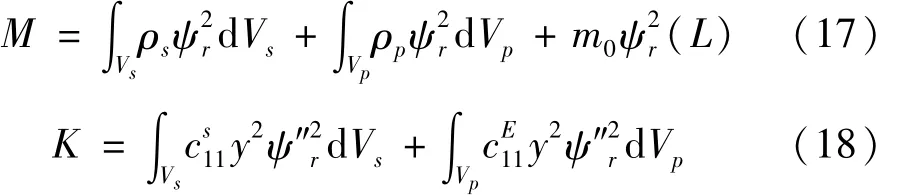
式中：θ和Cp分別是機電耦合系數和壓電元件的電容，定義如下：

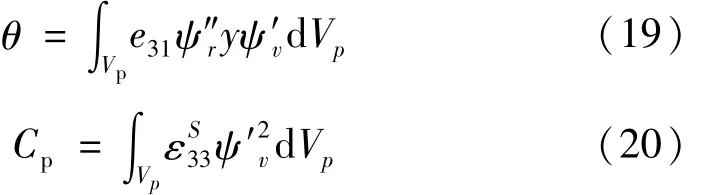
式中：N1、N2及N3則是方程非線性項的系數，定義為

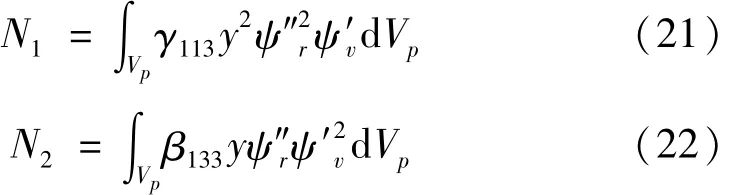
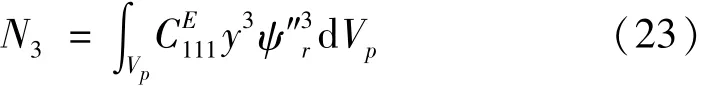
外部激勵項系數為

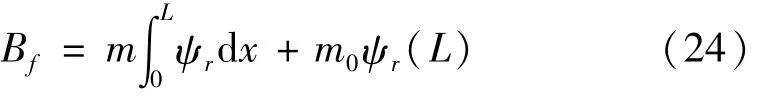
1．3 方程的化簡與無量綱化

設外加基礎激勵

式中：Ze是加速度幅值；Ωe是激勵頻率。假設負載電阻為純電阻RL時，電壓可表示為于是（15）、

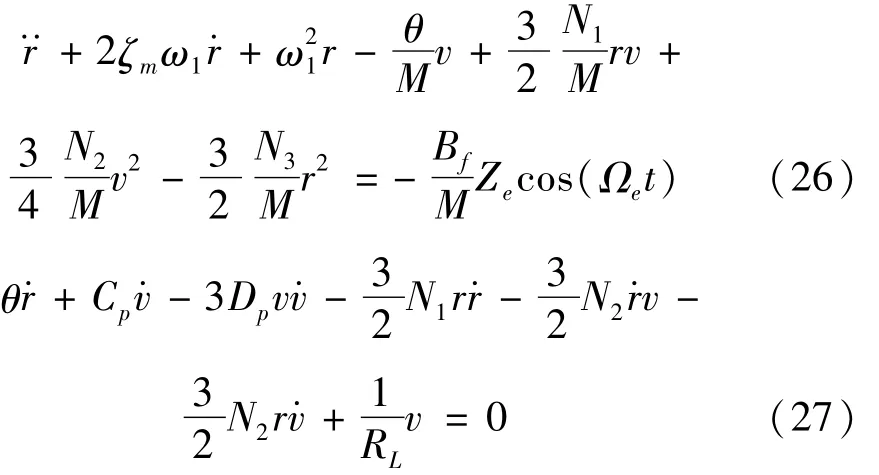
式中：為阻尼比。

為了對上述動力學方程進行無量綱化處理，定義特征時間、特征長度、特征電壓分別為

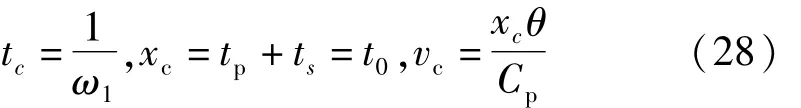
于是有 r＝xcx，v＝vcu，t＝tcτ，其中 x、u、τ為無量綱量。代入方程（26）、（27）后得到無量綱化的動力學方程

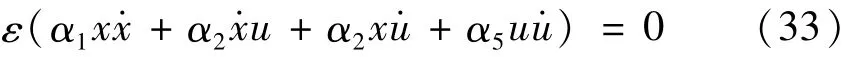
2 壓電層合梁的主共振響應

2.1 主共振的二次近似解

利用多尺度法求解系統主共振響應的二階近似解，設解如下

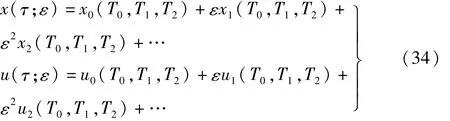
式中：Tj＝εjτ，（j＝0，1，2）。

考慮共振情況，對于方程（32）、（33），由于耦合項的存在使派生系統的固有頻率不再為1，引入調諧參數σ，令

式中：Λ為方程對應派生系統的固有頻率。將式（33）代入（31）、（32），令 ε同次冪系數相等，從而得到

方程組（36）由兩個耦合的常系數線性微分方程組成，故可令

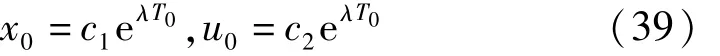
代入（36）中，得

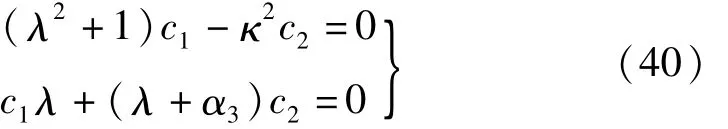
對于非平凡解，式（40）中的系數行列式必須為零，于是得

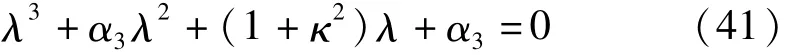
方程（41）根的判別式

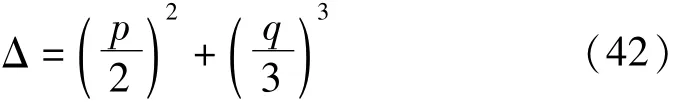
式中：cc表示共軛。

從式（47）第一式中消去產生永年項的那些項，要求 eiΛT0的系數為零得

或

于是（47）式化為

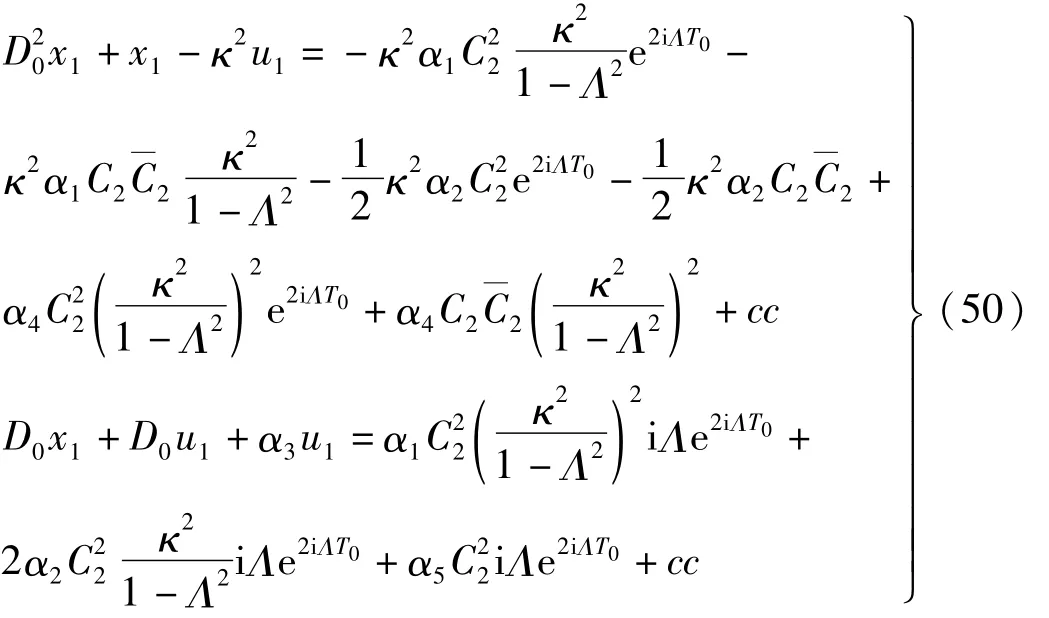
設式（50）的解為

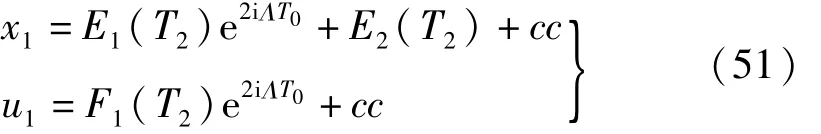
代入式（50），由對應系數相等可解出 E1、E2、F1，整理并簡寫如下：

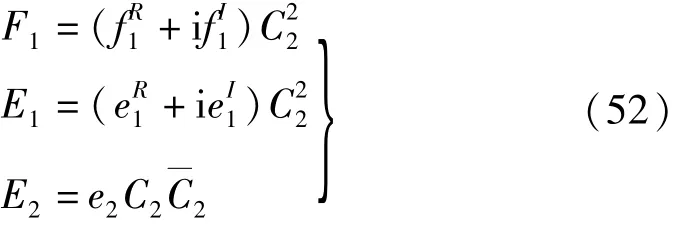
式中：系數詳見附錄 1。將式（45）、（51）代入式（38）中的第一式，并考慮 D1C2＝0得

2.2 響應定常解及其穩定性

隨著T2的增加，方程（55）中的a和γ在經歷一小段時間的振蕩后將趨向于定常值。為了考察系統的穩態運動，令 D2a＝0，D2γ＝0，得定常解振幅 a～和相位 γ～滿足方程

相頻響應方程為

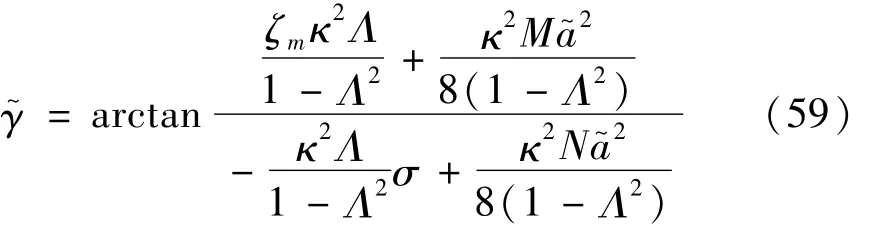
從而繪出系統主共振幅頻響應曲線如圖2所示。由圖可見，系統在共振點附近響應幅值較大，為了提高系統發電量，期望系統能工作在該區域內，稱為系統的工作區域。對于固定的激勵頻率（亦即σ），主共振可能是唯一的，也可能有三種。為了分析主共振的穩定性及其實現條件，將方程（55）在（a～，γ～）處線性化，形成關于擾動量Δa和Δγ的自治微分方程

根據式（62）可畫出主共振二次近似定常解的失穩域，如圖2所示陰影區域。顯然，失穩域對應幅頻響應曲線有多解時的中間解支。

圖3給出取σ＝－4時，由式（55）自不同的（a，γ）出發的相軌線，圖中的P1、P2、P3是三個奇點，對應圖2中σ為－4處的三個響應解。其中，P1、P3是穩定焦點，對應上下兩個穩定解；P2是鞍點，對應中間落在失穩域中的不穩定解。系統狀態最終被吸引到哪個奇點取決于系統的初始狀態。只有恰好位于兩區域分界線上的初始狀態才可能被吸引到P2，且一旦受到小擾動，便會偏離原軌道被吸引到P1或P3。對于壓電發電結構而言，通過選取合適的初始條件，使其工作在上解支，此時對應較大的響應幅值，從而提高發電量。

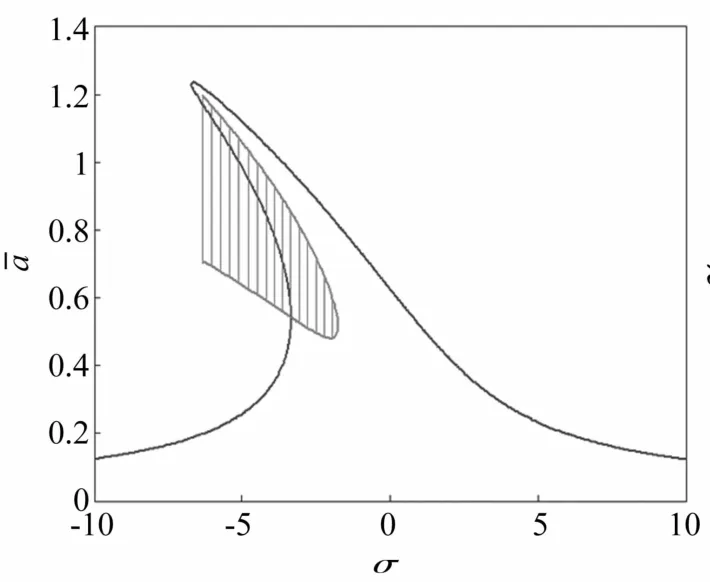
圖2 穩態主共振的幅頻響應及失穩域（陰影部分：不穩定）Fig．2 Proximate response of the primary resonance and its stability（shadow：unstable）

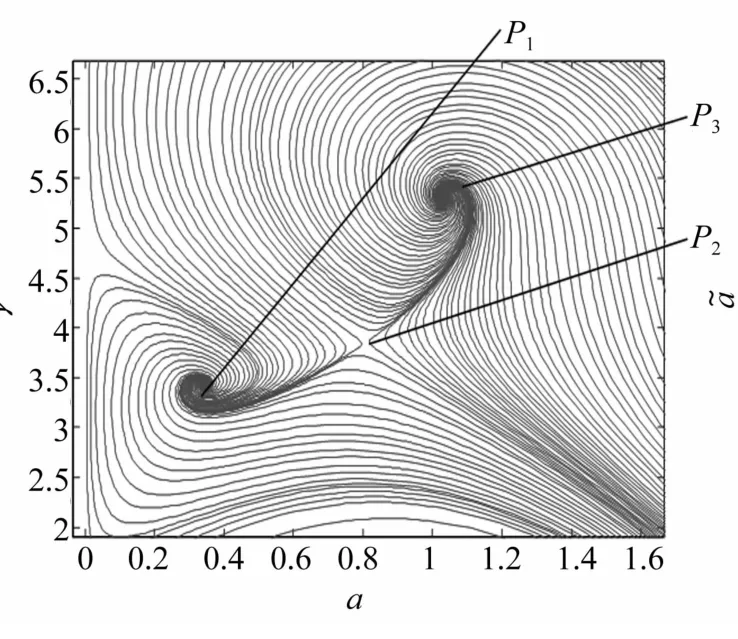
圖3 主共振響應解的吸引域（σ＝－4）Fig．3 Domain of attraction of primary resonance solution（σ＝－4）

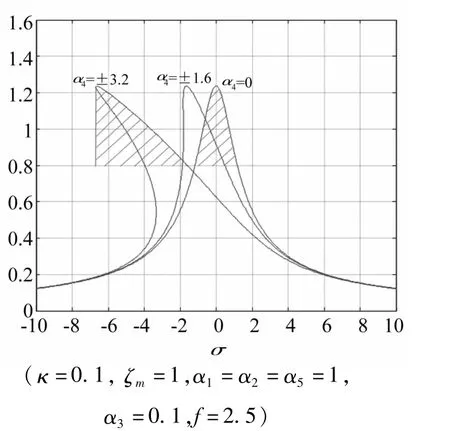
圖4 α4變化時穩態主共振的幅頻響應曲線Fig．4 Amplitude-frequency response of the primary resonance with differentα4

2．3 定常解響應分析

圖4給出主共振響應隨非線性剛度系數α4的變化曲線，當置方程二次非線性剛度系數α4＝0時，主共振只存在唯一解，且σ取0值附近時響應幅值較大（右邊陰影區域）；當α4不為0時，對于固定的σ，主共振存在多解現象；無論α4符號如何，近似解的共振峰總是左偏，呈現軟特性的非線性性質；隨著α4的增大，近似解的共振峰偏移增大，共振點對應頻率減小，且響應幅值隨頻率變化的速率變緩，這意味著在多值區域內，若能控制系統的響應解落在上解支，則系統的工作頻帶（左邊陰影區域）將明顯加寬。分析表明，壓電結構固有的材料非線性特性能有效降低結構的共振頻率，拓寬共振頻帶，這一點更有利于結構適應具有寬、低頻特點的環境振動。非線性是壓電材料的固有特性，在對壓電結構的設計中忽略這一特性，會導致結構的工作頻帶與環境振動頻帶的吻合性較差，發電效率降低。

取α4＝3．2，即考慮壓電材料非線性的影響，當激勵頻率調諧參數σ取不同值時，繪出激勵幅值f與響應幅值的關系曲線如圖5所示。當σ≥0時，不同的激勵振幅f對應唯一的響應幅值；而σ＜0時，當f取值較小時，a～出現多解和跳躍現象，隨著f的增大，a～恢復單解情況。因此，適當的增大外激勵幅值可避開多解區域，并有利于壓電結構發生較大的形變，從而提高發電量。

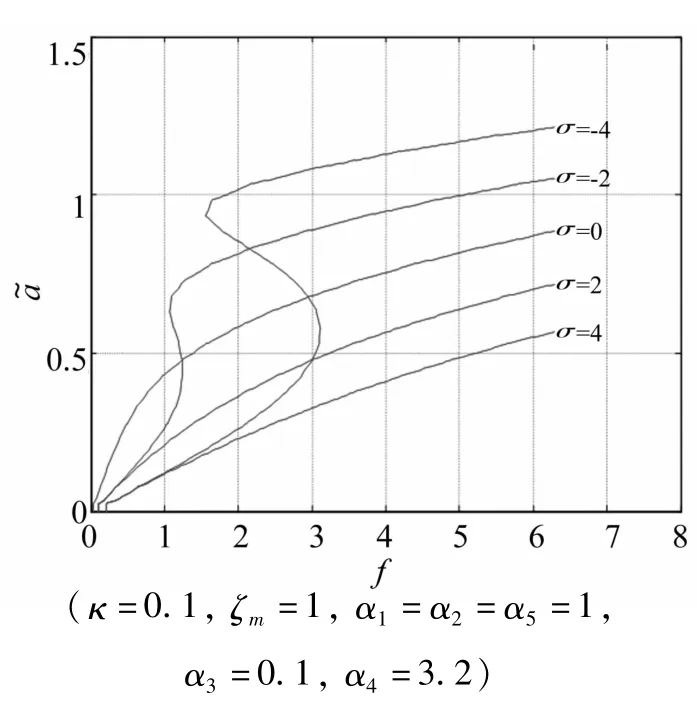
圖5 激勵幅值與穩態響應幅值的關系Fig．5 Steady state response-Excitation amplitude curves

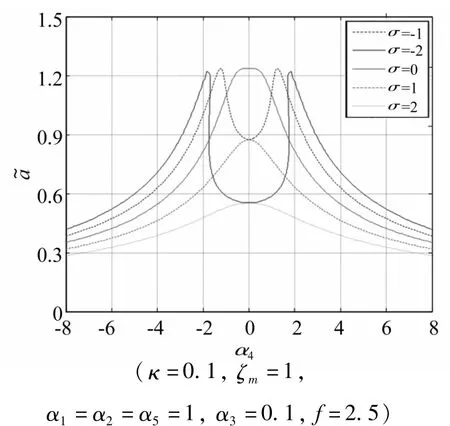
圖6 非線性剛度系數對穩態響應的影響Fig．6 The influence of nonlinear stiffness coefficients on the steady state response

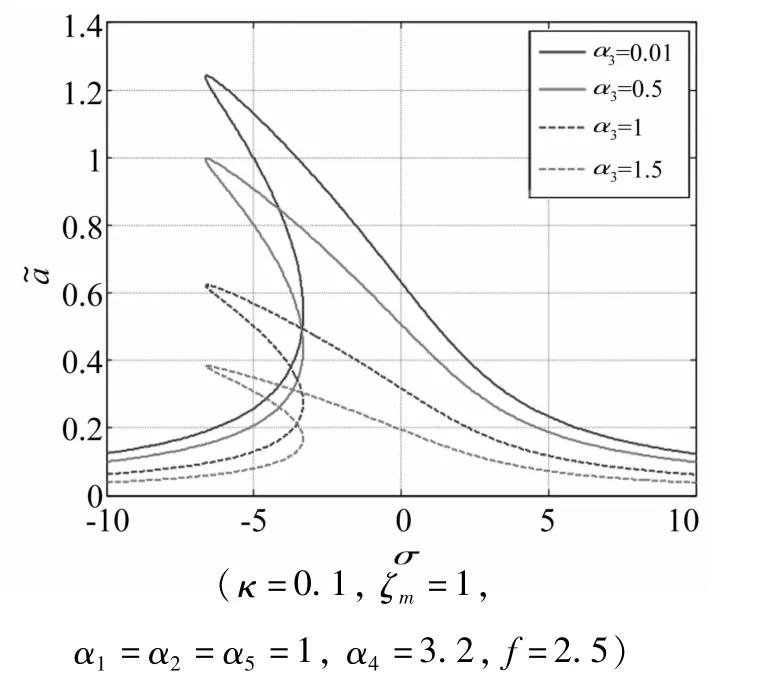
圖7 α3取不同值時系統的主共振響應Fig．7 Response of the primary resonance with differentα3

圖6則給出了激勵頻率調諧參數σ取不同值時，非線性剛度系數α4與響應幅值的關系曲線。從該圖可以看出，當外激勵頻率大于等于固有頻率，即σ≥0時，非線性的增強導致響應幅值減小；當σ＜0時，系統響應的峰值不再對應α4等于0處，而是發生偏移，隨著非線性的增強響應幅值先增后降。由此看出，當外激勵頻率大于系統固有頻率時，壓電材料非線性對系統響應起負面作用，而當外激勵頻率小于系統固有頻率時，二次非線性剛度系數α4取某特定值時系統響應最大。因此根據不同的應用場合選擇合適的壓電材料有利于提高發電量。

系數α3是與負載電阻成反比的參數，圖7給出了α3取不同值時系統的頻率響應曲線，圖8則給出了激勵頻率調諧參數σ取不同值時，負載電阻與系統輸出功率的關系。從圖中可以看出，隨著α3的增大，即負載電阻的減小，響應近似解的共振峰峰值減小，輸出功率則隨著負載電阻的增大先增后降，在60～100 kΩ時對應功率較大。分析表明，壓電發電系統存在一個最佳負載范圍，對應輸出功率較大，能量轉化效率較高。

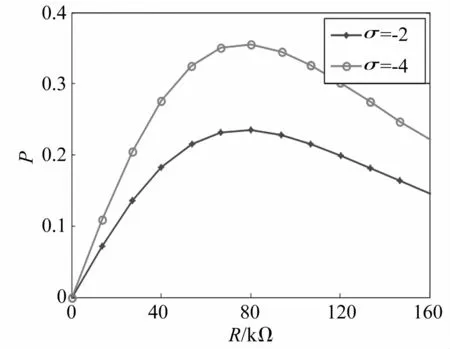
圖8 負載電阻與功率的關系曲線Fig．8 Power out-Load resistance curves

3 數值模擬驗證

通過數值方法驗證上述解析分析結論。取ε＝0．1，κ＝0．1，ζm＝1，α1＝1，α2＝1，α3＝0．1，α4＝3．2，α5＝1，f＝2．5，σ＝－4，對原方程（32）、（33）進行數值積分，得到系統穩態解的時間歷程圖并與求解所得的二次近似解（56）進行對比，如圖9所示。從圖上可以看出二次近似解析解與數值模擬的結果吻合較好。

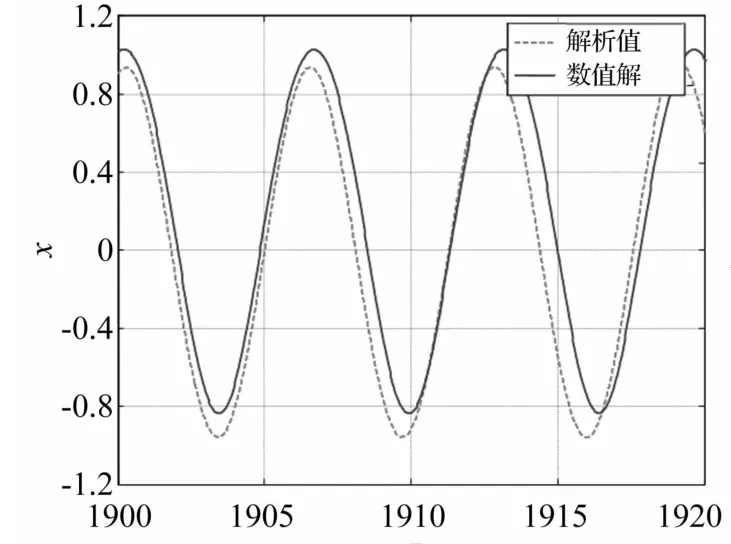
圖9 近似解與數值解對比（x（0），x·（0），u（0），u·（0））＝（1．5，0．5，0，0）Fig．9 Comparison of the approximate solution and numerical solution

圖10 系統主共振的跳躍現象（α1＝α2＝α5＝1，α4＝3．2）Fig．10 The jumping phenomenon of the primary resonance

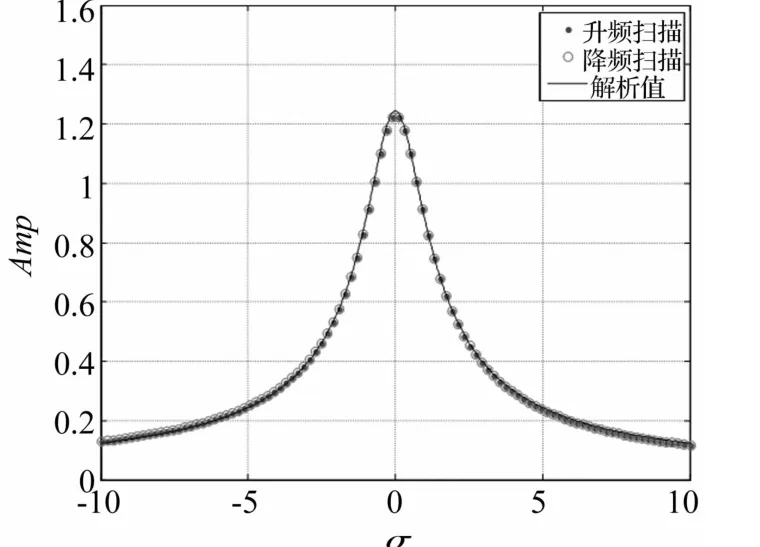
圖11 對應線性系統的主共振幅頻響應（α1＝α2＝α4＝α5＝0）Fig．11 Amplitude-frequency response of the primary resonance for linear system

為了驗證系統響應的多解及跳躍現象，搞清不同解支的穩定性，通過數值的方法對原方程（32）、（33）分別進行升、降頻掃描模擬，如圖10所示。從該圖可以看出，數值模擬的結果與解析分析的結果吻合較好。升頻掃描下系統響應在σ＝－3．737時向上跳躍；降頻掃描下則在σ＝－6．162處向下跳躍。在－3．737到－6．162區間內系統出現多解現象，上下兩個解支對應兩個穩定焦點，對于該區間內的某一固定σ而言，響應解落在上解支還是下解支取決于初始條件的選取。該結論與解析分析的結果一致。

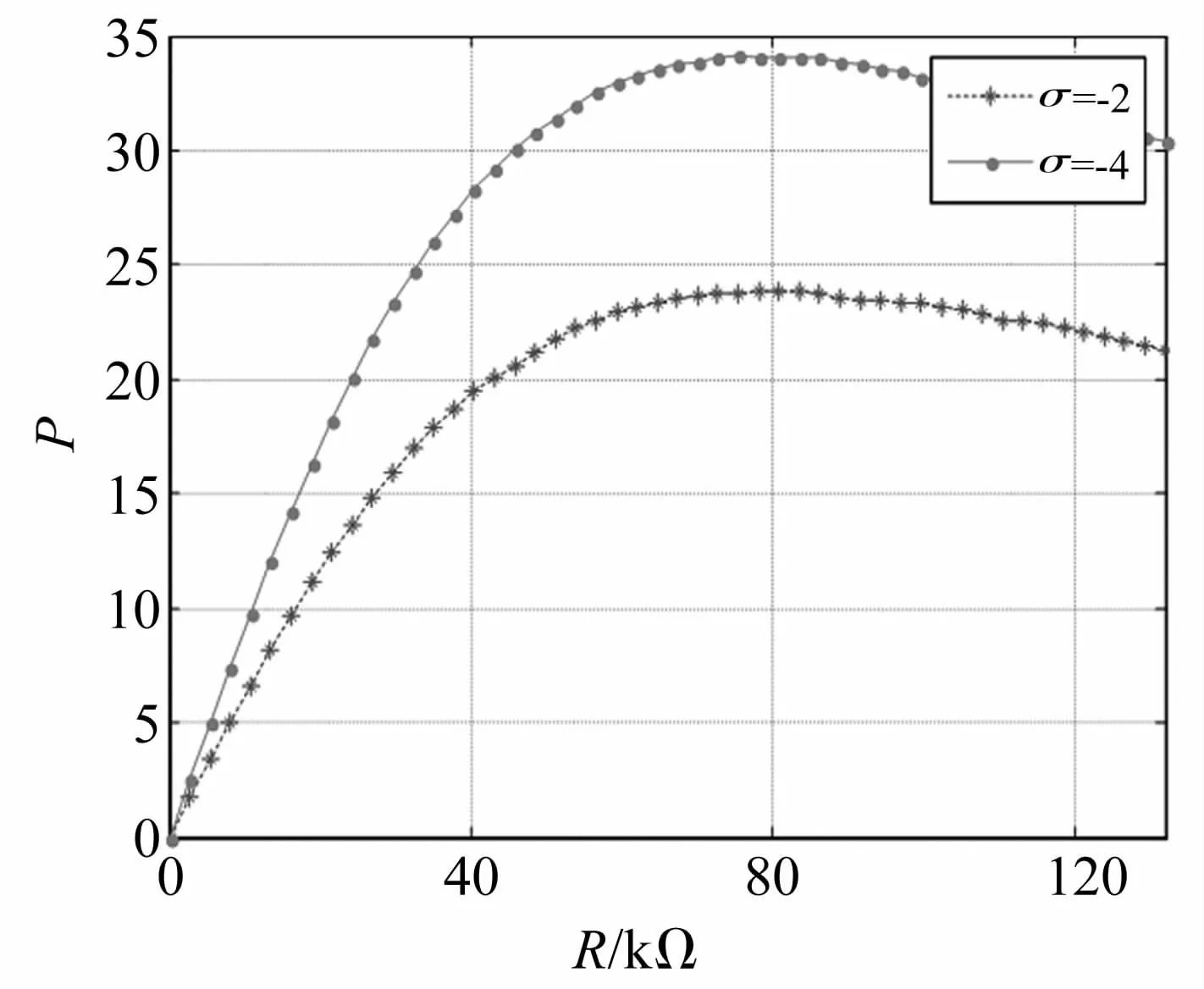
圖12 負載電阻與功率的關系曲線Fig．12 Power out-Load resistance curves

圖11給出了對應線性系統，即不考慮材料非線性影響時系統的主共振幅頻響應曲線，對比可以看出，正是由于壓電材料非線性的影響，系統主共振的幅頻響應曲線出現了共振峰偏移以及共振點附近的多解和跳躍現象，同時共振頻帶也明顯拓寬。由于壓電發電系統收集的是具有寬、低頻及隨機特點的周圍環境振動，拓寬共振頻帶有利于系統工作在近共振狀態，通過控制結構振動的初始條件，如加一個脈沖控制電路等方式使壓電結構在多解區域內的響應落在上解支，此時對應較大的響應幅值，從而提高發電量。

圖12給出了輸出功率隨負載電阻的變化曲線，如圖表明輸出功率隨負載電阻的增大先增后降，負載電阻在60－100 kΩ區間范圍內時輸出功率較大，具有較高的能量轉化效率，該結論與解析分析結論同樣一致。

4 結 論

本文考慮壓電材料的二次非線性本構關系，建立了帶有集中質量的懸臂式壓電發電結構的非線性動力學模型。利用多尺度法研究了系統的二次主共振響應，分析了系統的非線性項系數、外激勵參數及負載電阻對系統響應的影響規律，并通過數值分析對解析分析的結論進行了驗證，得到如下結論：

（1）壓電結構在主共振狀態下具有較大的振動幅值，可從外界提取更多的能量。此時壓電材料固有的非線性特性對結構主共振響應的影響較為突出，會導致系統的響應共振峰向左偏移，對應外激勵頻率小于系統的固有頻率。

（2）當外激勵頻率取不同值時，對應主共振響應解可能是唯一的，也可能是3個，分別對應2個穩定焦點和1個不穩定鞍點，由此解釋了外激勵頻率變化時響應振幅發生跳躍現象的原因；主共振響應解的真正實現取決于解的穩定性條件及初始條件的選取，通過控制系統工作的初始條件，使其工作在對應較大響應幅值的穩定解附近可提高發電量。

（3）壓電發電系統存在一個最佳負載電阻阻值范圍，對應輸出功率較大，能量轉化效率較高。

本文結論為深入研究壓電懸臂式發電系統的非線性動力學機理奠定一定的理論基礎，為結構設計中參數的選擇及發電性能的優化提供一定的理論依據。下一步將通過現場實驗測試，與解析和數值仿真的結果進行比較，并針對不同的振動環境，優化壓電懸臂梁的結構，以提高壓電發電系統的能量轉換效率。

［1］Williams C B，Yates R B．Analysis of a micro-electric generator for microsystems［J］．Sensors and Actuators A，1996，52：8－11．

［2］Glynne-Jones P， Tudor M J， Beeby S P， et al． An electromagnetic，vibration-powered generator for intelligent sensor systems［J］．Sensors and Actuators A，2004，110：344－349．

［3］Mitcheson P，Miao P，Start B，et al．MEMS electrostatic micro-power generator for low frequency operation［J］．Sensors and Actuators A，2004，115：523－529．

［4］Cook-Chennault K A，Thambi N，Sastry A M．Powering MEMS portable devices-a review of non-regenerative and regenerative power supply systems with special emphasis on piezoelectric energy harvesting systems［J］．Smart Materials and Structures，2008，17（4）：1－33．

［5］劉祥建，陳仁文．壓電振動能量收集裝置研究現狀及發展趨勢［J］．振動與沖擊，2012，31（16）：169－176．LIU Xiang-jian， CHEN Ren-wen． Current sitution and developing trend of piezoelectric vibration energy harvesters［J］．Journal of Vibration and Shock，2012，31（16）：169－176．

［6］邱清泉，肖立業，辛守喬，等．振動式微型發電機的研究進展［J］．振動與沖擊，2010，29（9）：191－195．QIU Qing-quan， XIAO Li-ye， XIN Shou-qiao，et al．Research progress on vibration powered microgenerator［J］．Journal of Vibration and Shock，2010，29（9）：191－195．

［7］Roundy S，Wright P K．A piezoelectric vibration based generator for wireless electronics［J］．Smart Materials and Structures，2004，13：1131－1142．

［8］Johnson T J，Charnegie D，Clark W W，et al．Energy harvesting from mechanical vibrations using piezoelectric cantilever beams［J］．International Society for Optical Engineering，2006，6169：61690D．

［9］Sodano H A，Park G，Inman D J．Estimation of electric charge output for piezoelectric energy harvesting［J］．Strain，2004，40：49－58．

［10］duToit N E．Modeling and design of a MEMS piezoelectric vibration energy harvester［D］．Cambridge：Massachusetts Institute of Technology，2005．

［11］Erturk A，Inman D J．An experimentally validated bimorph cantilever model for piezoelectric energy harvesting from base excitations［J］．Smart Materials and Structures，2009，18（2）：1－18．

［12］闞君武，唐可洪，王淑云，等．壓電懸臂梁發電裝置的建模與仿真分析［J］．光學精密工程，2008，16（1）：71－75．KAN Jun-wu，TANG Ke-hong，WANG Shu-yun，et al．Modeling and simulation of piezoelectic cantilever generators［J］．Optics and Precision Engineering，2008，16（1）：71－75．

［13］袁江波，謝濤，陳維山，等．懸臂梁壓電發電裝置的實驗研究［J］．振動與沖擊，2009，28（7）：69－72．YUAN Jiang-bo， XIE Tao， CHEN Wei-shan，et al．Experimental study on electricity-generating capacity for a piezoelectric cantilever［J］．Journal of Vibration and Shock，2009，28（7）：69－72．

［14］單小彪，袁江波，謝濤，等．不同截面形狀懸臂梁雙晶壓電振子發電能力建模與實驗研究［J］．振動與沖擊，2010，29（4）：177－180．SHAN Xiao-biao，YUAN Jiang-bo，XIE Tao，et al．Modeling and test of piezoelectric cantilever generators with different shapes［J］．Journal of Vibration and Shock，2010，29（4）：177－180．

［15］賀學鋒，杜志剛，趙興強，等．懸臂梁式壓電振動能采集器的建模及實驗驗證［J］．光學精密工程，2011，19（8）：1771－1778．HE Xue-feng， DU Zhi-gang， ZHAO Xing-qiang， et al．Modeling and experimental verification for cantilevered piezoelectric vibration energy harvester［J］．Optics and Precision Engineering，2011，19（8）：1771－1778．

［16］曹樹謙，高健．壓電層合圓板的非線性動力學模型與主共振響應［J］．天津大學學報，2007，40（2）：139－146．CAO Shu-qian，GAO Jian．Nonlinear dynamic model and primary resonance of piezoelectric laminated disk［J］．Journal of Tianjin University，2007，40（2）：139－146．

［17］Stanton S C，Erturk A，Mann B P，et al．Nonlinear piezoelectricity in electroelastic energy harvesters-Modeling and experimental identification［J］．Journal of Applied Physics，2010，108：1－9．

［18］Stanton S C， Erturk A， Mann B P， et al． On the manifestation and influence of material nonlinearity in electroelastic power generators［J］．Proceedings of the ASME conference on SMASIS，2010，3790：261－266．

［19］Abdelkefi A，Nayfeh A H，Hajj M R．Global nonlinear distributed-parameter model of parametrically excited piezoelectric energy harvesters［J］．Nonlinear Dynamic，2012，67：1147－1160．

［20］Joshi S P．Nonlinear constitutive relations for piezoceramic materials［J］． Smart Materials and Structures， 1992（1）：80－83．

［21］Gao J，Cao S Q．Second-order approximation of primary resonance of a disk-type piezoelectric stator for traveling wave vibration［J］．Nonlinear Dynamics，2010，61：591－603．

附錄