基于LMD的多尺度形態學在齒輪故障診斷中的應用

侯高雁，呂 勇，肖 涵，郝志強

（武漢科技大學 機械自動化學院，武漢 430081）

從非線性、非平穩信號中提取出旋轉機械的故障頻率一直是人們研究的熱點，齒輪故障振動信號是一種典型的非線性、非平穩信號。為了提取出齒輪的故障頻率，人們提出了很多有效的方法，如小波變換，希爾伯特變換，數學形態學等，小波變換在機械故障診斷中已經取得了較好的應用效果，但是對于小波基的選擇方面是一個難點，同時也存在傅里葉變換的局限性；Hilbert-Huang變換，由于Hilbert算子不可避免的加窗效應，使得解調結果出現非瞬時相應特性，增大解調誤差；數學形態學是由Matheron和Serra［1－2］共同創立的，是基于積分幾何和隨機集理論建立起來的有別于時域、頻域的數學方法。該方法在考察信號時使用結構元素探針，通過結構元素探針在信號中不斷移動，從而提取有用信號的沖擊特征。

雖然形態濾波算法具有很強的抑制脈沖干擾的能力，但抑制白噪聲的能力卻不足。針對這一不足，提出了一種基于局域均值分解（Local Mean Decomposition，LMD）的多尺度形態學解調方法，首先將采集的信號經過LMD分解，然后再用形態學濾波器提取故障頻率。LMD［3］方法是Smith新近提出的一種新的時頻分析方法，它將復雜的多分量信號分解為若干個乘積函數（Production Function，PF）的線性組合，每一PF分量由一個包絡信號和一個調頻信號相乘得到，包絡信號就是該PF分量的瞬時幅值，而PF分量的瞬時頻率可以由調頻信號求出［4］。通過LMD方法可以很好的濾除白噪聲信號，同時還可以獲得原始信號的全部調制信息，再用形態學差值濾波器提取出齒輪故障特征。結果表明該方法能夠有效的在含噪信號中提取出故障頻率特征。

1 多尺度形態學

數學形態學［2］分析是基于積分幾何和隨機集的不同于時域、頻域分析的非線性方法。該方法首先應用于圖像處理中，隨后在信號處理方面得到了廣泛的應用，如文獻［5－8］。

1.1 數學形態學基本運算

腐蝕和膨脹兩種算子是數學形態學的基本運算。設采樣得到的一維多值信號（待處理信號）f（n）和一維結構元素序列 g（n）的定義域分別為 Df＝｛0，1，2，…，N－1｝和 Dg＝｛0，1，2，…，M－1｝，其中 N和 M都是整數，且N＞M。

式中 m∈0，1，2，M－1。

數學形態學的開運算用于濾除信號上方的峰值噪聲，去除信號邊緣的毛刺；閉運算用于平滑或抑制信號下方的波谷噪聲，填補信號的漏洞和裂紋。

1.2 形態學濾波器和形態學結構元素

利用開運算和閉運算的組合可以構造形態學分析算法，本文將介紹兩種濾波器，AVG和DIF濾波器。

平均（AVG）濾波器：

差值（DIF）濾波器：

平均濾波器可以同時消除信號中的正、負沖擊，對信號起到平滑作用，而差值濾波器，可以提取信號中的正、負沖擊。

確定了形態學運算，結構元素的選取就起到了至關重要的作用，結構元素是形態學的基本算子，它的選擇在于其形狀和尺寸（大小）的確定。結構元素的形狀一般選擇對稱的結構，因為非對稱時運算會產生偏移，結構元素可以選擇為圓盤形、正方形、菱形、六邊形、線段形等，不同形狀的結構元素運算結果會有差異，應針對待處理信號的幾何形狀進行選擇。當確定了結構元素的形狀后，其尺寸大小就至關重要，結構元素尺寸太大，閉運算時目標之間互相干擾，造成過度粘連，開運算時造成假斷裂；過小時，閉運算不能實現裂口較大的斷裂邊緣連接，開運算不能實現較大凸起與粘連的去除。因此，為了有效地提取信號中不同尺度的形態特征，需要自適應地選擇結構元素及具有多尺度形態學分析的功能。

2 LMD方法

局域均值分解（Local Mean Decomposition，LMD）方法是JSmith［3］提出的一種新的信號分析方法LMD，該方法的實質就是將非平穩調制信號分解為若干個由包絡信號和純調頻信號乘積而得的PF分量，它能根據信號本身的特征進行自適應地分解，使得分解后的每個分量都具有一定的物理意義，能夠反映信號的內在本質，在機械故障診斷領域中得到了很好的應用［9－12］。對于任意原始信號 x（t），其具體分解算法如下［4］：

（1）找出x（t）所有的局部極值點ni，通過各極值點，分別計算出相鄰兩極值點ni和ni＋1的平均值mi和包絡估計值ai

（2）分別將所有相鄰兩個極值點的平均值mi和包絡估計值ai用直線連接，然后采用移動平均方法進行平滑處理，分別得到局部均值函數m11（t）和包絡估計函數 a11（t）。

（3）將局部均值函數 m11（t）從原始信號 x（t）中分離出來，得：

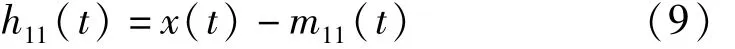
再用 h11（t）除以包絡估計函數 a11（t）以對 h11（t）進行解調，得：

對s11（t）重復上述步驟便能得到 s11（t）的包絡估計函數a12（t）。理想情況下，s11（t）是一個純調頻信號，它的包絡估計函數滿足 a12（t）＝1。如果 a12（t）不等于1，則將s11（t）作為原始數據重復以上迭代過程，直至s1n（t）為一個純調頻信號，即滿足 －1≤s1n（t）≤1，它的包絡估計函數滿足 a1（n＋1）（t）＝1。因此有以下公式：

式中：

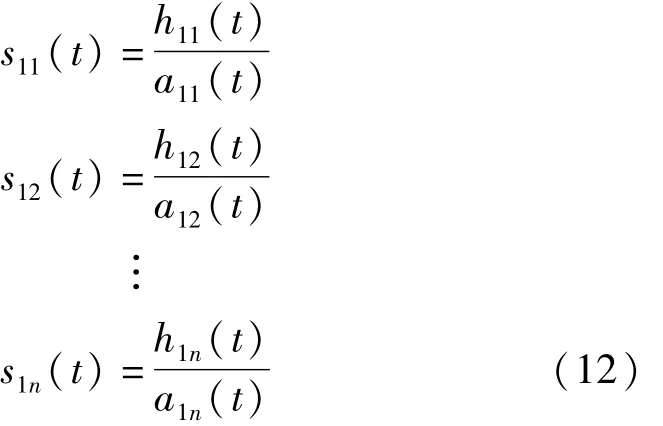
迭代終止條件為：

（4）把迭代過程中產生的所有局域包絡估計函數相乘便可以得到PF分量的包絡信號（瞬時幅值函數）。

（5）將包絡信號 a1（t）和純調頻信號 s1n（t）相乘便可以得到原始信號的第一個PF分量：

第一個PF分量包含了原始信號中最高的頻率成分，是一個單分量的調幅—調頻信號，而包絡信號a1（t）就是其瞬時幅值，其瞬時頻率 f1（t）可由純調頻信號 s1n（t）求出，即：

（6）PF的第一個分量PF1（t）從原始信號中分離出來，得到一個新的信號 u1（t），把 u1（t）作為原始數據重復上述步驟，循環 k次，直到uk為一個單調函數為止。

經過上述步驟，初始信號x（t）被分解為k個PF分量和uk（其中uk為殘余項）之和，即：

3 基于LMD的多尺度形態學

局部均值分解（LMD）是在EMD的基礎上提出的一種針對非線性非平穩信號的自適應時頻分析方法，它能根據信號自身的時間尺度特征自適應地將其分解，可將多分量的AM-FM信號分解為單分量的AM-FM信號，即由若干個PF分量組成，每一個PF分量都含有瞬時幅值和頻率，選取能量高的PF分量求和重構，采用多尺度形態學差值濾波器進行解調，提取出了故障頻率特征。此方法與EMD相比，LMD端點效應得到了一定的抑制，解決了欠包絡和過包絡的問題［13］。

數學形態學有很強的抑制脈沖干擾的能力，但濾除白噪聲的能力卻不足，LMD分解不僅可以濾除白噪聲，還可以有效地提取出故障特征頻率，將LMD與多尺度形態學相結合，用于提取故障信號的頻率特征，計算時間短，降噪效果好，能夠快速、準確地從故障信號中提取出故障頻率特征。

4 仿真實驗

為了驗證基于LMD的多尺度形態學解調方法提取信號沖擊成分，構造如下仿真信號進行分析：

其中，x1（t）＝cos（2*pi*30*t）＋1．5*cos（2*pi*50*t），頻率為 30和 50的諧波信號；x2（t）為標準差為1的高斯白噪聲；x3（t）為周期性的指數衰減沖擊信號（頻率為20 Hz，每周期內沖擊函數為exp（－20t）sin（20*pi*t）），對信號 y（t）進行采樣的頻率為 1 000 Hz，采樣點為10 000，得到的混合信號如下圖所示，圖1為混合信號的時域圖，圖2為混合信號的頻域圖。

圖1 混合信號的時域圖Fig．1 The time domain of Mixed signal

圖2 混合信號的頻域圖Fig．2 The frequency domain of Mixed signal

從圖1可以看出，沖擊信號淹沒在諧波信號和白噪聲信號中，圖2只能明顯的看出頻率為30 Hz和50 Hz的諧波信號，此實驗的目的是為了抑制諧波信號（30和50 Hz的余弦信號）和白噪聲，從而提取信號中的沖擊成分（即20 Hz的沖擊成分）。

先采用LMD對混合信號進行分解，LMD分解為6個PF分量，選取能量大的前三階PF分量，求和重構，便得到降噪后的信號，如圖3和圖4所示，圖3是經LMD降噪后的時域圖，圖4是相對應的頻域圖，將圖4與圖2對比，可以明顯的看到，經LMD處理后，達到了明顯的降噪效果。

圖3 混合信號經LMD降噪后的時域圖Fig．3 The time domain of Mixed signal after noise reduction by LMD

圖4 混合信號經LMD降噪后的頻域圖Fig．4 The frequency domain of Mixed signal after noise reduction by LMD

最后采用形態差值濾波器提取出沖擊頻率，如圖5所示，可以明顯的提取出20 Hz的沖擊信號及其2倍頻信號、3倍頻信號、4倍頻信號，證明了該方法的有效性。

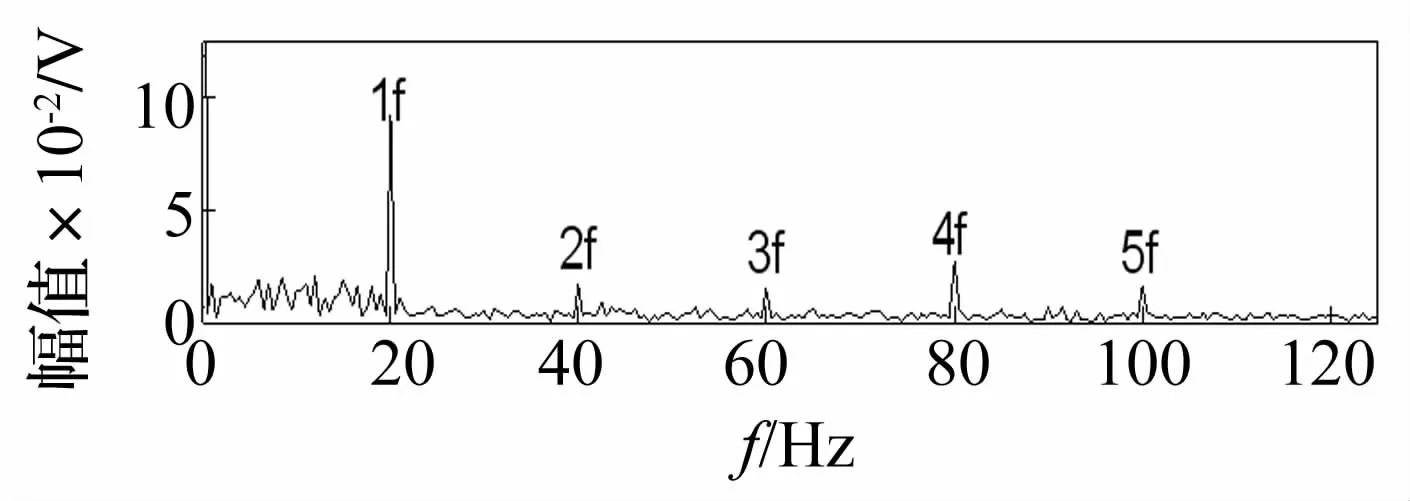
圖5 形態學提取后的結果Fig．5 The extraction result by the morphology

5 基于LMD的多尺度形態學在齒輪故障診斷中的應用

為了驗證所提出方法在齒輪箱故障特征提取中的有效性，在齒輪箱故障診斷試驗平臺上實驗。采用的齒輪箱變速為1級降速，該測試系統由調速電機、聯軸器、某型單級傳動齒輪箱、磁粉負載、傳感器和LMS分析儀組成。分別模擬齒輪斷齒和磨損兩種故障實驗，輸入軸和輸出軸的齒輪齒數分別為20和37，傳動比為1．85，齒輪模數為 3，高速軸的轉速為 363 r／min，采樣頻率為2 000 Hz，采樣點為10 000。

圖5（a）和圖5（b）分別為齒輪斷齒的時域圖和頻域圖，從圖中可以看出混有大量的噪聲，先對這些信號進行LMD分解，選取能量大的分量求和重構，然后用數學形態學差值濾波器來提取故障成分。

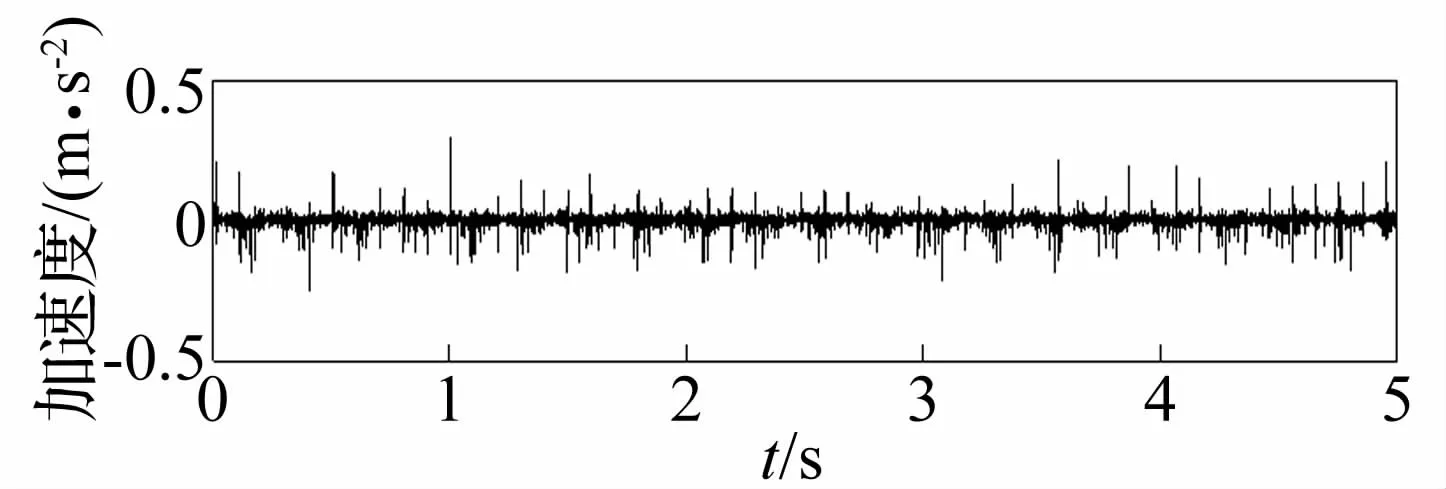
圖6（a） 齒輪斷齒時域圖Fig．6（a）The time domain of broken teeth of the gear

圖6（b） 齒輪磨損時域圖Fig．6（b）The frequency domain of broken teeth of the gear

圖7 斷齒信號經LMD分解后的前3項PF信息Fig．7 The former there PF information of the broken teeth signal after LMD decomposition

圖7為斷齒信號經LMD分解后形成的前3項能量較大的PF信息，將前3項PF信息求和重構，然后用形態學差值濾波器對重構的信息進行處理，提取出斷齒信號的故障頻率特征，如圖8所示，明顯的提取到了故障信號頻率為10 Hz的信息，以及2倍頻20 Hz，3倍頻30 Hz和1／2倍頻5 Hz等倍頻信息。

圖8 形態學提取后的結果Fig．8 The extraction result by the morphology

圖9（a）和圖9（b）分別為齒輪磨損信號的時域圖和頻域圖。齒輪磨損信號經LMD分解后，再用形態學差值濾波器處理后的結果，如圖10所示，提取到了故障信號的1倍頻（5 Hz）、2倍頻（10 Hz）和3倍頻（15 Hz）信號，證明了所提出的方法的有效性，能夠提取出信號的故障頻率特征。

圖9（a） 齒輪斷齒時域圖Fig．9（a）The time domain of wear and tear of the gear

圖9（b） 齒輪斷齒時域圖Fig．9（b）The frequency domain of wear and tear of the gear

圖10 形態學提取后的結果Fig．10 The extraction result by the morphology

6 結 論

LMD方法是一種自適應的時頻分析方法，該方法將多分量的振動信號自適應地分解得到一系列的PF分量，而每一個 PF分量實際上是一個單分量的調幅——調頻信號，它由一個包絡信號與一個純調頻信號相乘得到，從中選取能量大的PF分量進行求和重構，然后利用形態學差值濾波器提取故障信息。通過仿真試驗和模擬齒輪的斷齒和磨損實驗，證明了該方法的有效性。實驗表明，基于LMD多尺度形態學，可以有效提取齒輪的故障特征，實現齒輪的故障診斷。

［1］李兵，張培林，米雙山，等．機械故障信號的數學形態學分析與智能分類［M］．北京：國防工業出版社，2011．

［2］Serra J．Morphological filtering：an overwiew［J］．Signal Process，1994，38（4）：3－11．

［3］Smith SJ．The local mean decomposition and its application to EEG perception data［J］．Journal of the Royal Society Interface，2005，2（5）：443－454．

［4］程軍圣，楊怡，楊宇，等．基于LMD的能量算子解調機械故障診斷方法［J］．振動、測試與診斷，2012，32（6）：

915-919．CHENG Jun-sheng，YANG Yi，YANG Yu，et al．Energy operator demodulating machinery fault diagnosis method based on the LMD［J］．Vibration，test and diagnosis，2012，32（6）：915－919．

［5］Wang Jing， Xu Guang-hua， Application of improved morphological filter to the extraction of impulsive attenuation signals［J］．Mechanical Systems and Signal Processing，2009，23：236－245．

［6］章立軍，楊德斌，徐金梧，等．基于數學形態濾波的齒輪故障特征提取方法［J］．機械工程學報，2007，43（2）：71－75．ZHANG Li-jun，YANG De-bin，XU Jin-wu，et al．Approach to extracting gear fault feature based on mathematical morphological filtering［J］．Journal of Vibration and Shock，2007，43（2）：71－75．

［7］李兵，張培林，劉東升，等．基于自適應多尺度形態梯度變換的滾動軸承故障特征提取［J］．振動與沖擊，2011，30（10）：104－108．LI Bin，ZHANG Pei-lin，LIU Dong-sheng，et al．Feature extraction for roller bearing fault diagnosis based on adaptive multi-scale morphological gradient transformation［J］．Journal of Vibration and Shock，2011，30（10）：104－108．

［8］羅潔思，于德介，彭富強，等．基于EMD的多尺度形態學解調方法及其在機械故障診斷中的應用［J］．振動與沖擊，2009，28（11）：84－86．LUO Jie-si，YU De-jie，PENG Fu-qiang，et al．Multi-scale morphological demodulation method based on EMD and its application in mechanical fault diagnosis［J］．Journal of Vibration and Shock，2009，28（11）：84－86．

［9］程軍圣，史美麗，楊宇，等．基于LMD與神經網絡的滾動軸承故障診斷方法［J］．振動與沖擊，2010，29（8）：141－144．CHENG Jun-sheng，SHI Mei-li，YANG Yu，et al．LMD and neural network based fault diagnosis method of rolling bearing［J］．Journal of Vibration and Shock，2010，29（8）：141－144．

［10］何田，林意洲，郜普剛，等．局部均值分解在齒輪故障診斷中的應用研究［J］．振動與沖擊，2011，30（6）：196－201．HE Tian，LIN Yi-zhou，GAO Pu-gang，SHEN Yong-jun，et al．Local mean decomposition in the application of gear fault diagnosis research［J］．Journal of Vibration and Shock，2011，30（6）：196－201．

［11］Liu W Y，Zhang W H，Han JG，et al．A new wind turbine fault diagnosis method based on the local mean decomposition［J］．Renewable Energy，2012，48：411－415．

［12］張亢，程軍圣，楊宇．基于局部均值分解與形態學分形維數的滾動軸承故障診斷方法［J］．振動與沖擊，2013，32（9）：90－94．ZHANG Kang，CHENG Jun-sheng，YANG Yu．Roller bearing fault dignosis based on local mean decomposition and morphological fractal dimension［J］．Journal of Vibration and Shock，2013，32（9）：90－94．

［13］程軍圣，張亢，楊宇，等．局部均值分解與經驗模式分解的對比研究［J］．振動與沖擊，2009，28（5）：13－16．CHENG Jun-sheng， ZHANG Kang， YANG Yu， et al．Comparative study between local mean decomposition and empirical mode decomposition［J］．Journal of Vibration and Shock，2009，28（5）：13－16．