雙Y移30°PMSM兩電機(jī)串聯(lián)系統(tǒng)的諧波效應(yīng)

劉陵順， 張少一， 劉華菘

(海軍航空工程學(xué)院控制工程系，山東煙臺(tái) 264001)

0 引言

全電艦船、多電飛機(jī)概念的提出，以及機(jī)車牽引、機(jī)器人、紡織、造紙等工業(yè)用電系統(tǒng)的應(yīng)用要求，需要研究解耦運(yùn)行的多電機(jī)交流傳動(dòng)系統(tǒng)，為此提出了一種基于廣義零序諧波分量的單逆變器驅(qū)動(dòng)雙Y移30°PMSM兩電機(jī)串聯(lián)系統(tǒng)。該系統(tǒng)是由兩臺(tái)雙Y移30°PMSM按照一定的定子繞組聯(lián)結(jié)規(guī)則串聯(lián)而成，可在同一逆變器和同一套控制平臺(tái)下實(shí)現(xiàn)各臺(tái)電機(jī)的解耦運(yùn)行，有助于節(jié)省控制驅(qū)動(dòng)裝置及其外圍電路，降低了系統(tǒng)的體積、重量與成本。目前對(duì)于單逆變器驅(qū)動(dòng)多電機(jī)串聯(lián)系統(tǒng)的研究多以原理可行性探索為主，研究對(duì)象主要集中在多相感應(yīng)電動(dòng)機(jī)串聯(lián)系統(tǒng)，對(duì)于多相PMSM串聯(lián)系統(tǒng)的研究還較為少見［1］，已有文獻(xiàn)主要研究了理想正弦波磁場(chǎng)分布下多電機(jī)串聯(lián)系統(tǒng)的基本原理和控制策略［2－5］。由于電機(jī)的實(shí)際氣隙磁場(chǎng)通常存在著一系列的高次諧波，將對(duì)串聯(lián)系統(tǒng)的解耦控制產(chǎn)生影響。為此，文獻(xiàn)［6］采用虛擬多電機(jī)機(jī)電耦合的概念就五相PMSM反電動(dòng)勢(shì)諧波對(duì)串聯(lián)系統(tǒng)矢量控制的影響進(jìn)行了分析，文獻(xiàn)［7］分別研究了2臺(tái)五相電機(jī)串聯(lián)系統(tǒng)以及對(duì)稱六相串聯(lián)三相電機(jī)系統(tǒng)的定子繞組設(shè)計(jì)特點(diǎn)。考慮到雙Y移電機(jī)可靠性更強(qiáng)，其力矩脈動(dòng)平均值只有對(duì)稱六相電機(jī)的14%，諧波電流較小，雙Y移30°PMSM兩電機(jī)串聯(lián)系統(tǒng)具有更大的軍事應(yīng)用價(jià)值。本文以定子集中繞組的雙Y移30°PMSM為研究對(duì)象，利用繞組函數(shù)的概念，研究了不同類別的高次空間諧波與另一臺(tái)相串聯(lián)的雙Y移30°PMSM基波磁動(dòng)勢(shì)相互作用對(duì)系統(tǒng)解耦運(yùn)行產(chǎn)生的影響規(guī)律，建立了該串聯(lián)系統(tǒng)中其中一臺(tái)PMSM包含5、7次空間諧波的多維空間數(shù)學(xué)模型，進(jìn)行了變速、變負(fù)載的仿真研究，揭示了該串聯(lián)系統(tǒng)多相PMSM定子繞組必須為正弦波分布的根本原因。

1 高次空間諧波的耦合效應(yīng)分析

正弦波分布的雙Y移30°PMSM基于自然坐標(biāo)系下的數(shù)學(xué)模型經(jīng)過全維空間解耦矩陣運(yùn)算后，變換到由dq－xy－o1o23個(gè)正交基組成的正交平面上，其中電機(jī)的電磁轉(zhuǎn)矩完全是由dq電流分量決定，而與它們的xy電流分量和o1o2零序分量無(wú)關(guān)［8－12］。因此，雙Y移30°PMSM的磁通和轉(zhuǎn)矩控制只需要dq平面上的兩個(gè)電流分量即可，而xy平面的2個(gè)電流分量可以用來(lái)控制另一臺(tái)雙Y移30°PMSM，為此需將另一臺(tái)電機(jī)的定子繞組與第一臺(tái)電機(jī)的定子繞組通過適當(dāng)?shù)南嘈蜣D(zhuǎn)換串聯(lián)在一起，保證第一臺(tái)電機(jī)的磁通和轉(zhuǎn)矩生成電流分量不會(huì)在在第二臺(tái)電機(jī)中生成磁通和轉(zhuǎn)矩，反之亦然。2臺(tái)雙Y移30°PMSM串聯(lián)系統(tǒng)與逆變器的聯(lián)結(jié)圖如圖1所示。

為了分析圖1串聯(lián)PMSM定子繞組必須為正弦分布，下面利用PMSM1含有所有諧波的集中繞組研究各類諧波對(duì)解耦運(yùn)行的影響情況，假設(shè)定子繞組分布不對(duì)稱，則PMSM1中的高次諧波主要有:12i±1次(i=1，2，3，…)以及6i±1次(i=1，3，5，…)兩大類奇次諧波以及各偶次諧波。

圖1 兩臺(tái)雙Y移30°PMSM串聯(lián)系統(tǒng)Fig.1 Dual Y shift 30°PMSM series-connected system

根據(jù)圖1中的聯(lián)結(jié)關(guān)系，假設(shè)兩臺(tái)電機(jī)的基波電流的初始相位為零，則可得逆變器輸出電流與2

臺(tái)串聯(lián)電機(jī)電流的關(guān)系為［7］

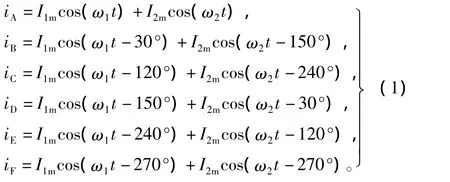
其中，I1m，I2m分別為2臺(tái)電機(jī)基波電流分量的幅值，ω1，ω2分別為2臺(tái)電機(jī)基波電流分量的角頻率。

假定PMSM1短距集中繞組下a相的繞組函數(shù)如圖2所示。

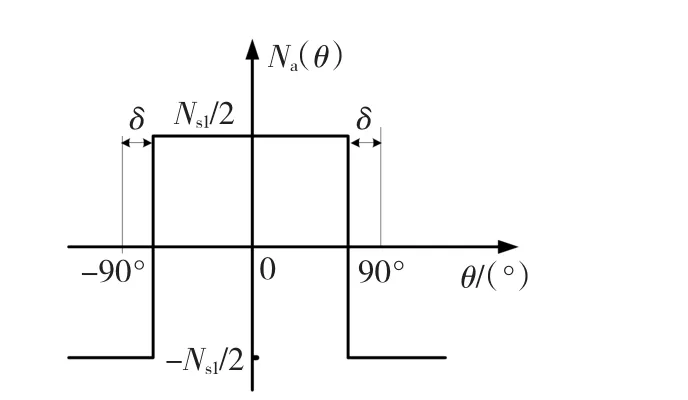
圖2 短距集中繞組下a相的繞組函數(shù)波形Fig.2 Winding function waveform of short-pitched concentrated coil

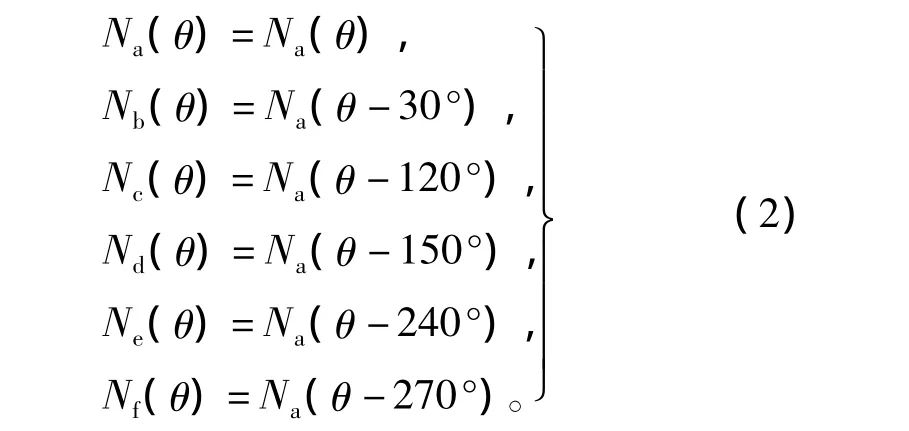
設(shè)PMSM1每相繞組的總有效匝數(shù)為Ns1，δ為短距角度，各相繞組函數(shù)之間的關(guān)系為

所以PMSM1定子繞組的傅里葉函數(shù)推導(dǎo)為

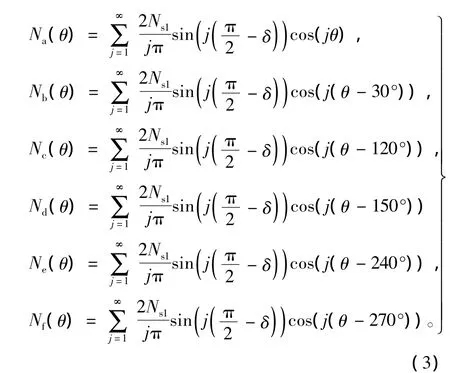
利用式(1)中PMSM2的磁通、轉(zhuǎn)矩基波電流以及式(3)，可得PMSM1中的第j次諧波與PMSM2基波電流產(chǎn)生的磁動(dòng)勢(shì)表達(dá)式為

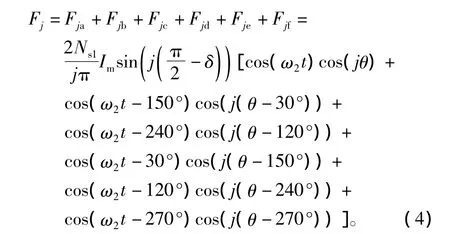
據(jù)此可以推導(dǎo)出PMSM1氣隙磁場(chǎng)中各類諧波與PMSM2的耦合作用，具體討論如下:

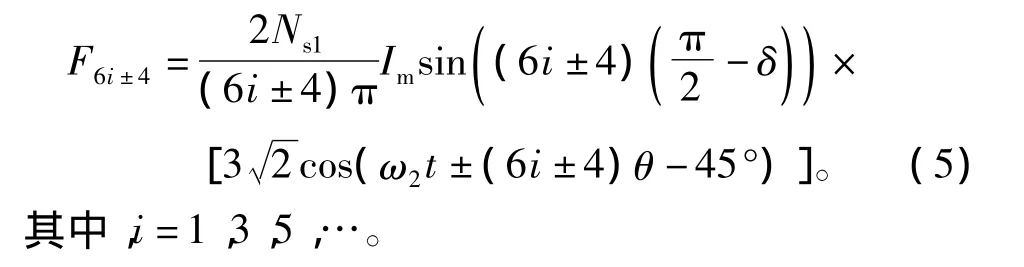
據(jù)此，PMSM1的(6i±4)次諧波(i=1，3，5，…)與PMSM2的基波電流耦合在PMSM1內(nèi)產(chǎn)生旋轉(zhuǎn)磁場(chǎng)。(6i+4)次諧波產(chǎn)生的旋轉(zhuǎn)磁場(chǎng)轉(zhuǎn)向與PMSM2的基波磁場(chǎng)相反，(6i－4)次諧波產(chǎn)生的旋轉(zhuǎn)磁場(chǎng)轉(zhuǎn)向與PMSM2的基波磁場(chǎng)相同。

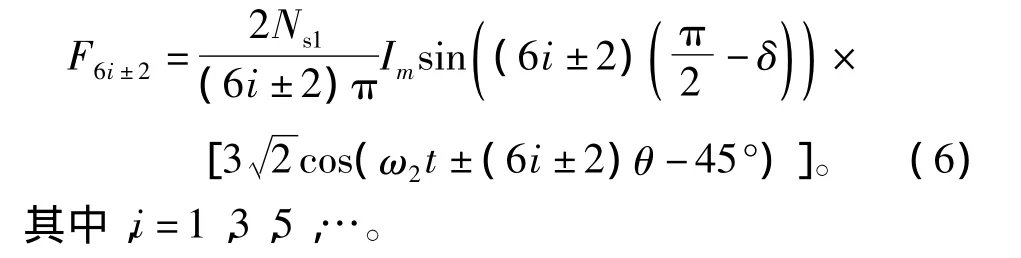
據(jù)此，PMSM1的(6i±2)次諧波(i=1，3，5，…)，與PMSM2的基波電流耦合在PMSM1內(nèi)產(chǎn)生旋轉(zhuǎn)磁場(chǎng)。(6i+2)次諧波產(chǎn)生的旋轉(zhuǎn)磁場(chǎng)轉(zhuǎn)向與PMSM2基波磁場(chǎng)相同。(6i－2)次諧波產(chǎn)生的旋轉(zhuǎn)磁場(chǎng)轉(zhuǎn)向與PMSM2基波磁場(chǎng)相反。

同理，對(duì)于PMSM1中的奇次諧波與PMSM2的

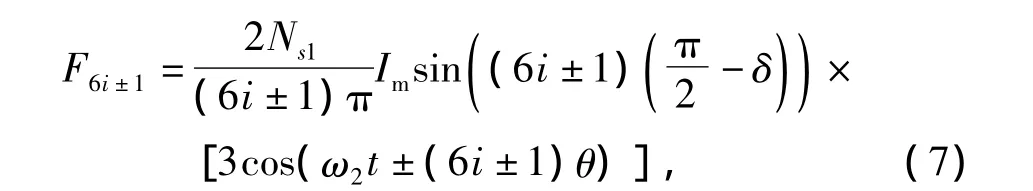
其中，i=1，3，5，…。

(6i±1)次諧波(i=1，3，5，…)與PMSM2的基波電流耦合在PMSM1內(nèi)產(chǎn)生旋轉(zhuǎn)磁場(chǎng)。其中(6i+1)次諧波產(chǎn)生的旋轉(zhuǎn)磁場(chǎng)轉(zhuǎn)向與PMSM2的基波磁場(chǎng)相反，(6i－1)次諧波產(chǎn)生的旋轉(zhuǎn)磁場(chǎng)轉(zhuǎn)向與PMSM2基波磁場(chǎng)相同。

此外，(12i±1)次奇次諧波(1，11，13，23，25…)以及3的倍數(shù)次諧波，將不會(huì)與PMSM2的基波電流產(chǎn)生耦合，因而，其產(chǎn)生的旋轉(zhuǎn)磁動(dòng)勢(shì)為零。

由此可見，PMSM2的基波電流與PMSM1的某些高次諧波互相耦合，在PMSM1中產(chǎn)生旋轉(zhuǎn)磁動(dòng)勢(shì)，其旋轉(zhuǎn)速度由兩臺(tái)串聯(lián)電機(jī)的同步轉(zhuǎn)速ω1和ω2共同控制，通常情況下 ω2與 ω1不相等，會(huì)在PMSM1中產(chǎn)生電磁轉(zhuǎn)矩脈動(dòng)，從而影響PMSM1的正常運(yùn)行。因此，在該串聯(lián)系統(tǒng)中，務(wù)必要求兩臺(tái)串聯(lián)電機(jī)的磁場(chǎng)分布呈正弦波，且在空間對(duì)稱分布，從而消除各偶次諧波以及(6i±1)次奇次諧波，i=1，3，5，…。

另外，盡管PMSM1中的(12i±1)次諧波不與PMSM2的基波電流耦合產(chǎn)生旋轉(zhuǎn)磁動(dòng)勢(shì)，但它們會(huì)與自身的基波電流分量作用產(chǎn)生高次轉(zhuǎn)矩紋波，因此，在電機(jī)設(shè)計(jì)中需要消除這些諧波。基波電流相互耦合的效果分析如下:

25 、7次空間諧波對(duì)解耦控制的影響仿真

2.1 含5、7次諧波的串聯(lián)系統(tǒng)數(shù)學(xué)模型

通常電機(jī)的定子繞組呈對(duì)稱分布，偶次諧波自然消失。為了驗(yàn)證串聯(lián)電機(jī)的(6i±1)奇次諧波(i=1，3，5，…)，對(duì)該串聯(lián)系統(tǒng)運(yùn)行存在的耦合問題，假定PMSM1中包含5、7次諧波(其他更高次諧波由于幅值過小可忽略)，PMSM2中氣隙磁場(chǎng)只有基波，不存在高次諧波。

設(shè)Ns1Ns1為PMSM1的每相定子繞組匝數(shù)，φfm1φfm1為PMSM1永磁主磁通，θr1為PMSM1轉(zhuǎn)子磁場(chǎng)軸線與定子A相繞組軸線之間的電角度，φfm1－5為PMSM1的5次諧波磁通，φfm1－7為PMSM1的7次諧波磁通，Ns1－5為PMSM1的5次諧波等效繞組匝數(shù)，Ns1－7為PMSM1的7次諧波等效繞組匝數(shù)，Ns2為PMSM2的定子繞組匝數(shù)，φfm2為PMSM2永磁主磁通，θr2為PMSM2轉(zhuǎn)子磁場(chǎng)軸線與定子A相繞組軸線之間的電角度。

PMSM1的轉(zhuǎn)子磁場(chǎng)與定子繞組交鏈的磁鏈為

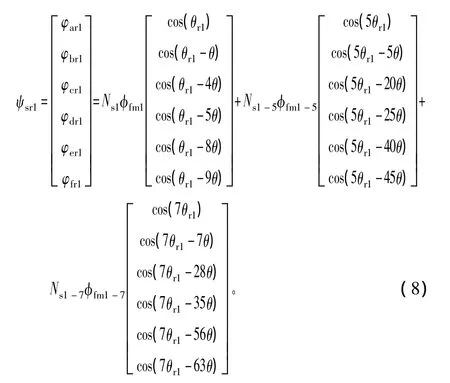
PMSM2轉(zhuǎn)子磁場(chǎng)交鏈在定子各相繞組中的磁鏈為

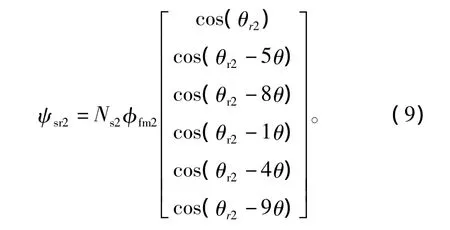
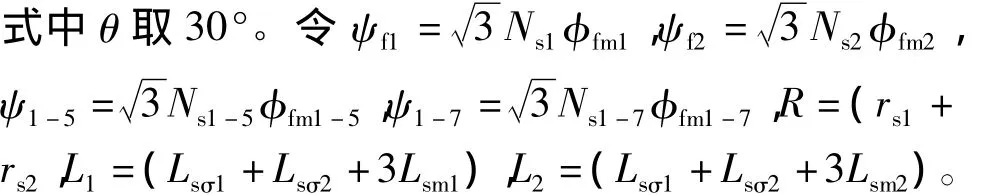
經(jīng)同步旋轉(zhuǎn)坐標(biāo)變換后，可推出PMSM1和PMSM2電壓方程為

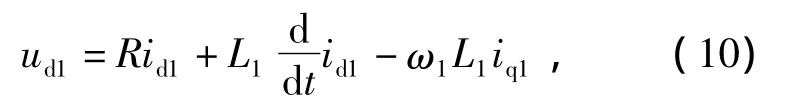
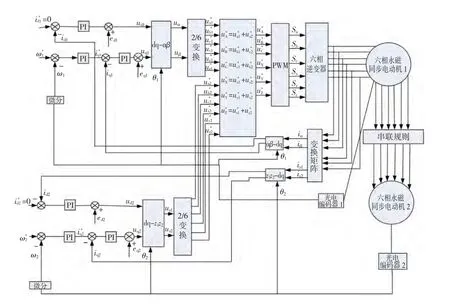
圖3 串聯(lián)系統(tǒng)基于id=0的矢量控制系統(tǒng)圖Fig.3 Vector control system based on id=0 for series-connected system

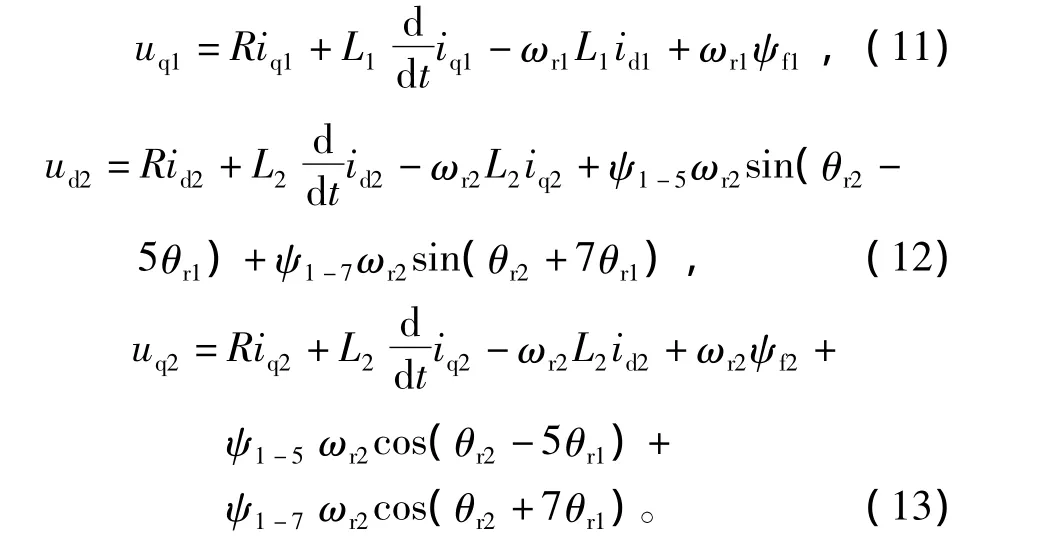
PMSM1和PMSM2的轉(zhuǎn)矩方程分別為

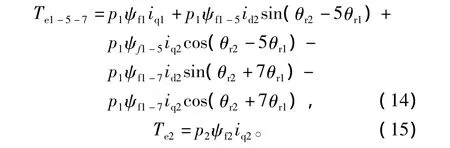
分析式(14)、式(15)可見，在PMSM2的id2或iq2id2非零時(shí)，PMSM1的電磁轉(zhuǎn)矩必有脈動(dòng)，脈動(dòng)幅值主要與id2、iq2以及空間諧波 ψ1－5、ψ1－7的大小相關(guān)，脈動(dòng)的頻率和2臺(tái)電機(jī)的轉(zhuǎn)速都相關(guān)。PMSM2的轉(zhuǎn)矩只與自身的iq2和ψf2有關(guān)，不受PMSM1的空間諧波影響。

2.2 PMSM1含5、7次諧波串聯(lián)系統(tǒng)耦合性能仿真

為了驗(yàn)證PMSM1含有的5、7次空間諧波會(huì)影響串聯(lián)系統(tǒng)的解耦控制，采用id=0的載波調(diào)制

PWM矢量控制策略對(duì)2臺(tái)雙Y移30°PMSM串聯(lián)系統(tǒng)建模仿真，如圖3所示。參數(shù)設(shè)置:極數(shù)p1=p2=4，磁通 ψf1=ψf2=0.2 Wb，ψ1－5=0.08 Wb，ψ1－7=0.06 Wb，摩擦系數(shù)B1=B2=0.05，轉(zhuǎn)動(dòng)慣量J1=J2=0.1 kg·m2，R1=R2=2.875 Ω，L1=L2=0.12 H。

PMSM1變負(fù)載仿真如圖4所示:PMSM1含5、7次空間諧波，初始負(fù)載為1 N·m，在1 s從1 N·m增加到10 N·m，轉(zhuǎn)速為200 r/min;PMSM2不含諧波，負(fù)載為2 N·m不變，轉(zhuǎn)速為250 r/min。

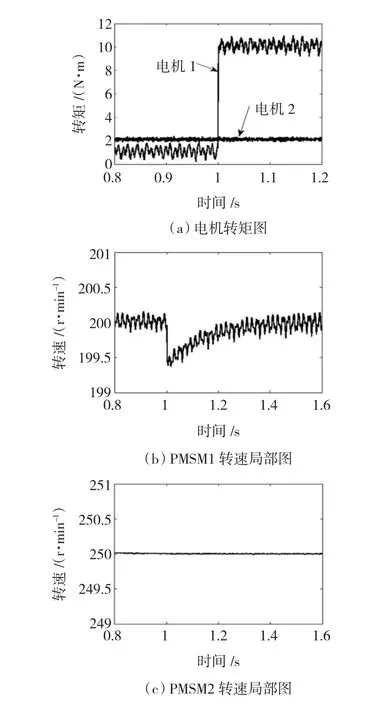
圖4 PMSM1變負(fù)載運(yùn)行Fig.4 Variable load operating of PMSM1

由以上仿真可知:

1)當(dāng)PMSM1含5、7次空間諧波，PMSM2只有基波時(shí)，只要PMSM2帶負(fù)載，即iq2存在，PMSM1就存在轉(zhuǎn)矩和轉(zhuǎn)速脈動(dòng)，脈動(dòng)的頻率和幅值與PMSM1的負(fù)載變化無(wú)關(guān)。

2)PMSM1的負(fù)載增加對(duì)PMSM2的轉(zhuǎn)速和轉(zhuǎn)矩均無(wú)影響，這說明不含空間諧波的PMSM2在該串聯(lián)系統(tǒng)中不受PMSM1的變載影響。

3)PMSM1的負(fù)載在1 s增加時(shí)，其轉(zhuǎn)速小幅下降并迅速恢復(fù)。

PMSM2變負(fù)載仿真如圖5所示:PMSM1含5、7次空間諧波，空載不變，轉(zhuǎn)速設(shè)為200 r/min;PMSM2不含諧波，負(fù)載為2 N·m，在1 s時(shí)從2 N·m變?yōu)?0 N·m，轉(zhuǎn)速設(shè)為250 r/min。

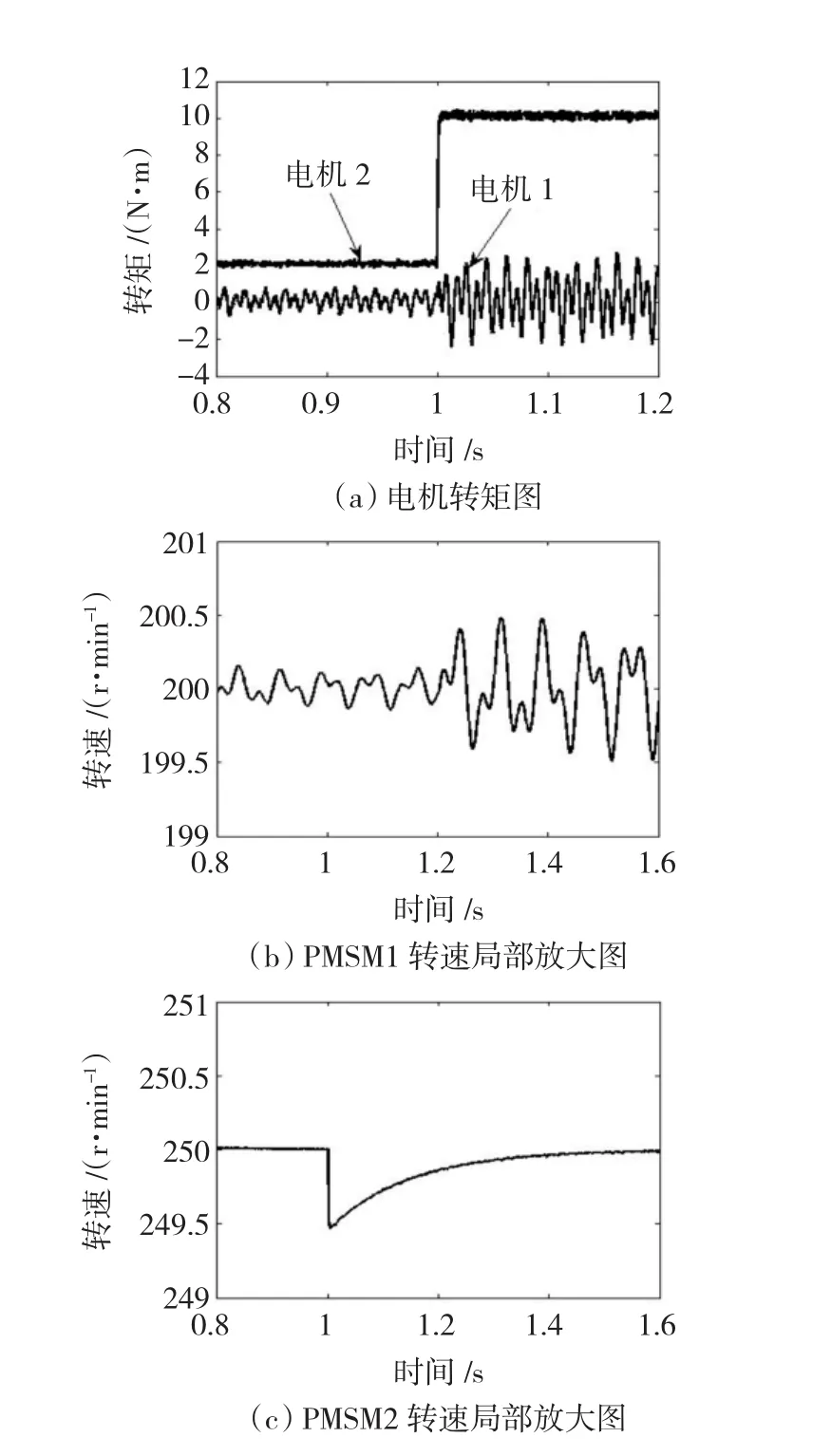
圖5 PMSM2變負(fù)載運(yùn)行Fig.5 Variable load operating of PMSM2

1)PMSM2的負(fù)載增大后，PMSM1的轉(zhuǎn)矩和轉(zhuǎn)速脈動(dòng)幅值都增大，即PMSM1的轉(zhuǎn)矩和轉(zhuǎn)速脈動(dòng)幅值受PMSM2的負(fù)載影響，脈動(dòng)頻率與PMSM2的負(fù)載大小無(wú)關(guān)。

2)PMSM2在1s負(fù)載增加后轉(zhuǎn)速小幅下降，并迅速恢復(fù)。且不含諧波的PMSM2負(fù)載變化時(shí)，其自身的轉(zhuǎn)矩和轉(zhuǎn)速不存在任何脈動(dòng)。

PMSM1變速仿真如圖6所示:PMSM1含5、7次空間諧波，且空載運(yùn)行，初始給定為200 r/min，在0.9 s從200 r/min加速到350 r/min;PMSM2不含諧波，其負(fù)載為2 N·m，給定轉(zhuǎn)速為250 r/min。

1)PMSM1的轉(zhuǎn)速增加對(duì)PMSM2的轉(zhuǎn)速、轉(zhuǎn)矩均無(wú)影響，這說明不含空間諧波的PMSM2在該串聯(lián)系統(tǒng)中不受PMSM1的變速影響。

2)比較PMSM1變速前后的轉(zhuǎn)速圖，PMSM1的轉(zhuǎn)速增加使其轉(zhuǎn)速脈動(dòng)的頻率有所升高。

PMSM2變速仿真如圖7所示:PMSM1含5、7次空間諧波，且空載運(yùn)行，給定轉(zhuǎn)速為200 r/min;PMSM2不含諧波，其負(fù)載為2 N·m，在0.9 s從100 r/min加速到400 r/min。

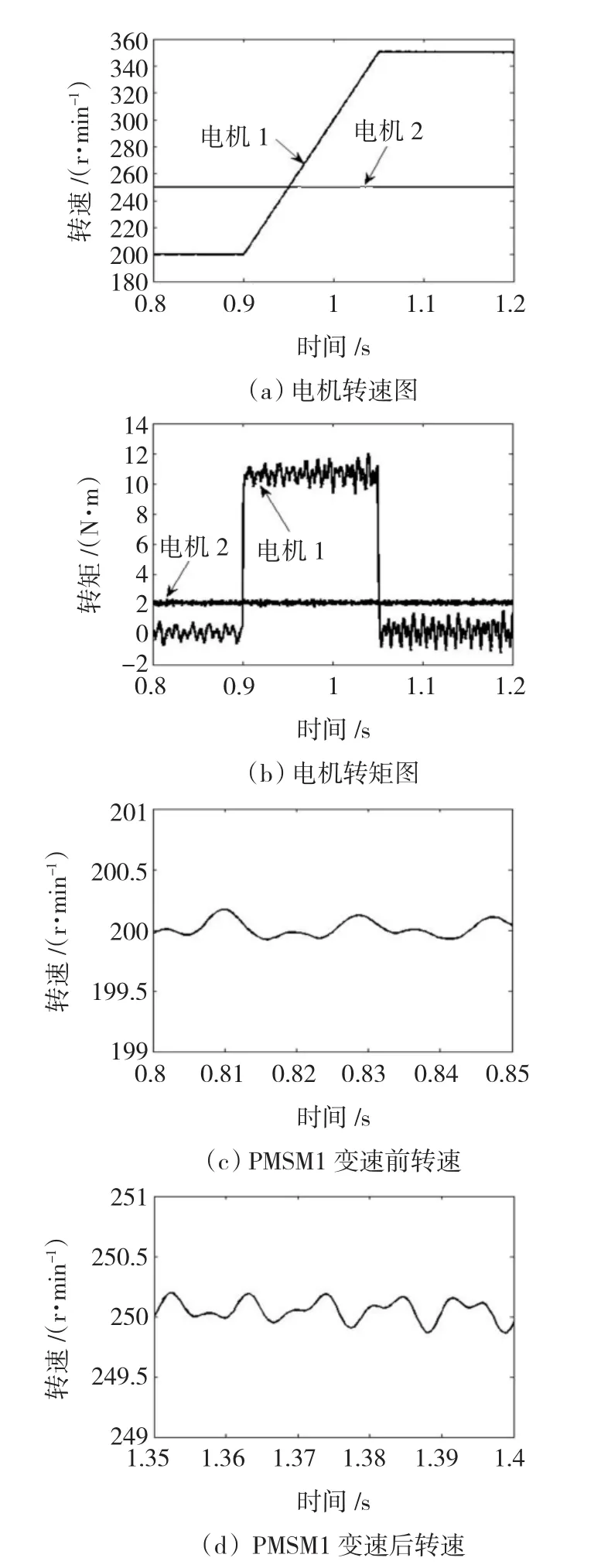
圖6 PMSM1變速運(yùn)行Fig.6 Variable speed operating of PMSM1

在PMSM2的轉(zhuǎn)速增加過程中，PMSM1的轉(zhuǎn)矩脈動(dòng)幅值和頻率均有所增大。但PMSM2的轉(zhuǎn)速和轉(zhuǎn)矩均不存在脈動(dòng)。

從以上仿真可以得出結(jié)論:

1)含5、7次空間諧波的PMSM1轉(zhuǎn)矩脈動(dòng)與PMSM2的負(fù)載大小有關(guān)，脈動(dòng)頻率與PMSM1以及PMSM2的轉(zhuǎn)速都相關(guān)，因此該串聯(lián)系統(tǒng)中PMSM1的運(yùn)行是不解耦的。

2)若PMSM2不含空間諧波，其運(yùn)行不受PMSM1變載變速的影響。因此，若實(shí)現(xiàn)該串聯(lián)系統(tǒng)中2臺(tái)電機(jī)的解耦運(yùn)行，每臺(tái)電機(jī)均不能包含(6i±1)奇次諧波(i=1，3，5，…)。

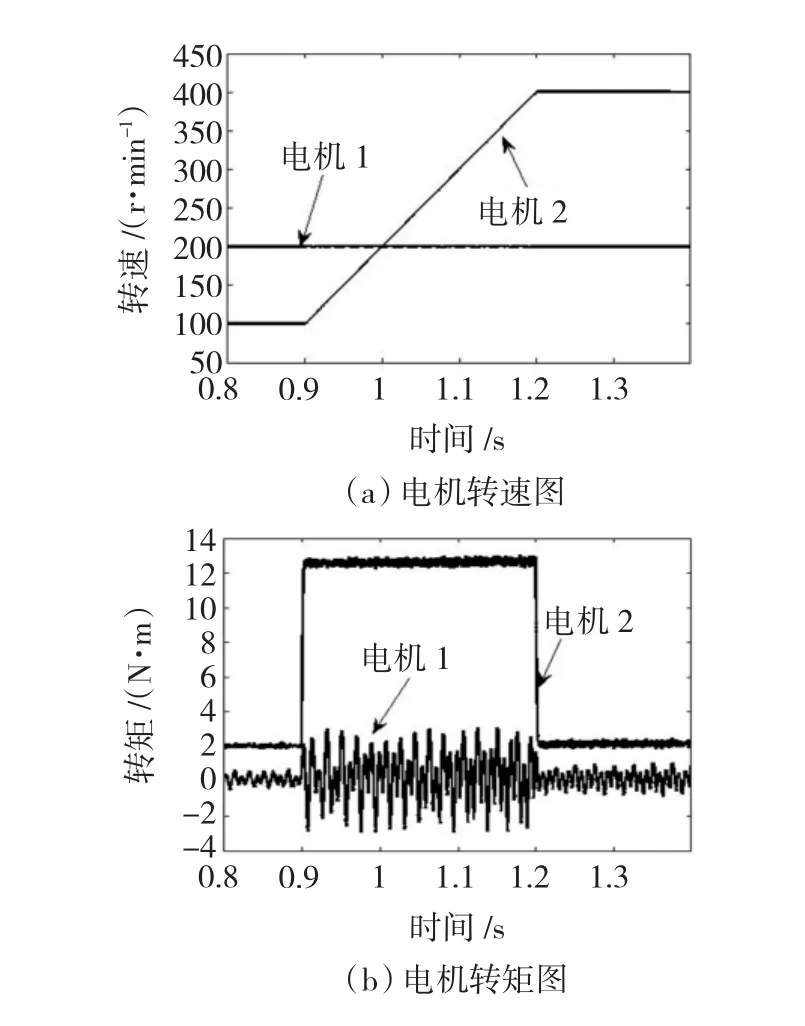
圖7 PMSM2變速運(yùn)行Fig.7 Variable speed operating of PMSM2

3 結(jié)語(yǔ)

為了分析電機(jī)高次空間諧波對(duì)串聯(lián)系統(tǒng)解耦運(yùn)行的影響規(guī)律，本文建立了雙Y移30°六相PMSM集中繞組函數(shù)的傅里葉變換式，利用PMSM1高次諧波與PMSM2基波電流耦合的磁動(dòng)勢(shì)關(guān)系式，分析了不同類別的高次諧波對(duì)串聯(lián)系統(tǒng)解耦運(yùn)行的影響規(guī)律，建立了該串聯(lián)系統(tǒng)的數(shù)學(xué)模型并進(jìn)行了變速、變負(fù)載仿真，提出了串聯(lián)系統(tǒng)多相PMSM定子繞組必須為正弦波分布的必然要求，為電機(jī)的優(yōu)化設(shè)計(jì)及空間諧波補(bǔ)償?shù)慕怦羁刂铺峁├碚摶A(chǔ)。

［1］LEVI E.Multiphase electric machines for variable-speed applications［J］.IEEE Transactions on Industrial Electronics，2008，55(5):1893－1909.

［2］LEVI E，JONES M.A novel concept of a multiphase multimotor vector controlled drive system supplied from a single voltage source inverter［J］.IEEE Transactions on Power Electronics，2004，19(2):320－335.

［3］LEVI E，JONES M，VUKOSAVIC S N，et al.Operating principles of a novel multiphase multimotor vector-controlled drive［J］.IEEE Transactions on Energy Conversion，2004，19(3):508－517.

［4］IQBAL A，LEVI E.Space vector PWM for a five-phase VSI supplying two five-phase series-connected machines［C］//12th International Power Electronics and Motion Control Conference，August 30－September 1，2006，Portoroz，Slovenia.2006:222－227.

［5］LEVI E.Even-phase multi-motor vector controlled driver with single inverter supply and series connection of stator windings［J］.IEE Proceedings-Electric Power Applications，2003，150(5):580－591.

［6］SEMAIL E，LEVI E，BOUSCAYROL A，et al.Multi-machine modeling of two series connected 5-phase synchronous machines:effect of harmonics on control［C］//European Conference on Power Electronics and Applications，September 11－14，2005，Dresden，Germany.2005:1－10.

［7］LEVI E，JONES M，VUKOSAVIC S N，et al.Stator winding design for multi-phase two-motor drives with single VSI supply［C］//International Conference on Electrical Machines，September 2－5，2006，Chania，Greece.2006:CD－ROM Paper No.OMM2－1.

［8］艾永樂，王玉梅，KAMPER Marrten.梯形波相電流控制的六相感應(yīng)電機(jī)建模與控制［J］.電機(jī)與控制學(xué)報(bào)，2012，16(3):71－76.

AI Yongle，WANG Yumei，KAMPER Marrten.Modeling and controlling of six-phase induction machine driven trapezoidal phase current waveform［J］.Electric Machines and Control，2012，16(3):71－76.

［9］彭兵，王成元，夏加寬.六相永磁力矩伺服電機(jī)氣隙磁場(chǎng)優(yōu)化［J］.電機(jī)與控制學(xué)報(bào)，2011，15(12):39－42.

PENG Bing，WANG Chengyuan，XIA Jiakuan.Air-gap magnetic field optimization for six-phase permanent magnet torque servo motor［J］.Electric Machines and Control，2011，15(12):39－42.

［10］楊金波，楊貴杰，李鐵才.雙三相永磁同步電機(jī)的建模與矢量控制［J］.電機(jī)與控制學(xué)報(bào)，2010，14(6):1－7.

YANG Jinbo，YANG Guijie，LI Tiecai，Modeling and vector control for dual three-phase PMSM［J］.Electric Machines and Control，2010，14(6):1－7.

［11］歐陽(yáng)紅林，成蘭仙.多相永磁同步電機(jī)模糊神經(jīng)網(wǎng)絡(luò)控制調(diào)速系統(tǒng)［J］.電機(jī)與控制學(xué)報(bào)，2007，11(2):111－115.

OUYANG Honglin，CHENG Lanxian.Multiple phase permanent magnet synchronous motor speed control system based on fuzzy neural network control［J］.Electric Machines and Control，2007，11(2):111－115.

［12］趙品志，楊貴杰，李勇.三次諧波注入式五相永磁同步電機(jī)轉(zhuǎn)矩密度優(yōu)化［J］.中國(guó)電機(jī)工程學(xué)報(bào)，2010，30(33):71－77.

ZHAO Pinzhi，YANG Guijie，LI Yong.Torque density optimization for five-phase PMSM with third harmonic injection［J］.Proceedings of the CSEE，2010，30(33):71－77.