讓數學教學充滿邏輯的力量

張衛星

數學邏輯力量是指一種至高無上的、合乎思維規律與數學發展規律、蘊含著邏輯必然的力量，是一種數學地、有條理地思考和解決問題的力量，是一種扎根于數學靈魂深處的理性精神。只有讓數學教學充滿邏輯的力量，才能讓數學教學嚴謹有序，彰顯“數學味”，從而達到用數學知識本身的魅力吸引學生的目的。那么，怎樣才能讓數學教學充滿邏輯的力量呢？下面，筆者以兩次教學實踐為例闡述自己的粗淺看法。

一、 讓例題之間充滿邏輯力量

“用比例解決問題”是學生在對比例的基本性質有了一定的建構基礎以及掌握了正、反比例的意義的背景下進行探索學習的。教材中的例1是有關繳水費的實際問題（如圖1），例2是有關圖書打包的實際問題（如圖2）。例1側重于用正比例方法解決，例2側重于用反比例方法解決。課后的“做一做”安排了兩道有關購買圓珠筆的實際問題（如圖3）。

教材的本意是通過對一些生活實際問題的解決，讓學生領悟到用比例解決問題的必要性及一般方法，但筆者始終認為上述兩個例題存在一定的缺陷。第一個缺陷是例題中的素材與學生生活實際存在嚴重脫節。例1中的“求水費”，即使對城市學生來說，也是比較陌生的。因為現如今的水費都是自來水公司給你算好了，用戶只要到銀行繳費就行了。對農村學生來說，更是沒有一點印象。因為農村的用水基本上是地下水，無須繳水費。例2中的“圖書打包”，對城市及農村的學生來說都是陌生的，因為圖書打包是成人的工作，對小學生特別是農村的小學生來說根本就沒有看到過。第二個缺陷是兩個例題之間的素材缺乏內在的邏輯聯系。“求水費”和“圖書打包”之間沒有關聯性，不利于學生對兩個例題進行比較、分析與思考。而“做一做”中的兩個習題卻完全消除了上述的兩個缺陷，“買圓珠筆”素材學生非常熟悉，而且兩個習題用同一素材，使兩個例題之間具有可比性。更為可喜的是題1是單價一定，而題2是總價一定，兩個數量關系之間有著緊密的內在的邏輯聯系，容易組織學生對這兩個例題進行比較、分析與思考。

基于上述解讀，筆者對教材進行了適當處理：把“做一做”中的兩個習題當做例題進行教學，而把例1、例2當作學生自學的材料，在學生自學的基礎上進行解疑問難。為了讓學生感悟例題之間的內在邏輯聯系，筆者經歷了如下的教學片斷：

師：例1是用正比例方法解決的，例2是用反比例方法解決的，你們認為這兩個例題之間有什么聯系？

生1：例1和例2都是講買圓珠筆的事情。

生2：例1是單價一定，所以用正比例方法解決。例2是總價一定，所以用反比例方法解決。

生3：單價一定，就是總價和數量的比值一定，所以用正比例方法解決。總價一定，就是單價和數量的積一定，所以用反比例方法解決。

生4：兩道例題中三個相關聯的量是相同的。

生5：兩道例題都是先找相關聯的量，接著確定哪個量一定，然后決定兩個量成什么比例，最后決定用什么比例方法解決。

生6：兩個例題的解題步驟也差不多。

……

通過學生“你一言，我一語”的發言，學生對兩個例題之間的內在聯系——邏輯聯系有了本質的認識。在此基礎上，再去自學原先教材中的兩個例題，大部分學生都能學懂。可見，讓例題之間充滿邏輯的力量，可以產生意想不到的效果。

二、 讓知識之間充滿邏輯力量

“24時記時法”是在學生認識了鐘面，學習了時、分、秒等有關知識后學習的一種記時法。它在現實生活中的用途比較廣泛，與學生的生活聯系非常密切，通過學習可以幫助學生建立正確的時間觀念，養成合理安排時間、珍惜寶貴時間的好習慣。此課教學的難點是讓學生厘清“24時記時法”和“普通記時法”之間的內在聯系與區別。教材用如下這段話（如圖4）來說明兩者之間的關系。

教材的本意是讓學生知道上午的時刻改成24時記時法，時刻數保持不變，下午和晚上的時刻改成24時記時法，要把時刻數加12，才等于新的時刻數。同時也告訴學生普通計時法的時刻前面有時間定語，而24時記時法的時刻前面不能加時間定語。因此，在把普通計時法改成24時記時法后，時刻前面的時間定語全部取消。教材中的三個例子雖然很有代表性，但對三年級學生來說，例子的數量實在太少了，學生很難自己領會到。而且教材中也沒有涉及普通記時法，兩種記時法之間的邏輯聯系無法有效溝通，學生也無法對普通記時法和24時記時法進行全面比較。

基于對教材的深入分析，筆者認為教學時必須將普通記時法和24時記時法進行全面比較，促使學生在解讀兩者的區別與聯系中領會兩者之間固有的、內在的邏輯聯系，從而深刻把握24時記時法的本質。為此，筆者經歷了如下的教學片斷：

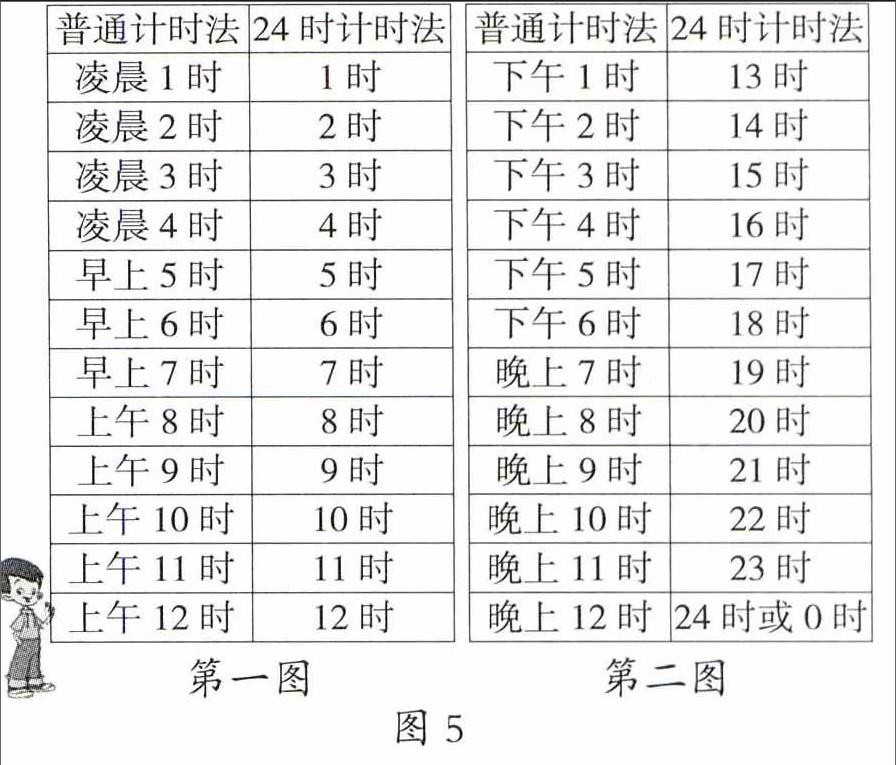
師生一起完成下圖（圖5）：

師：觀察這幅圖，你有什么話要說？

生1：普通記時法都有時間詞語，而24時記時法沒有。

生2：1～4時是指凌晨；5～7時是指早上；8～11時是指上午；12時指中午；13時～18時是指下午；19時～24時是指晚上。

生3：晚上12時就是24時或0時。

生4：凌晨到中午的普通記時法的時刻數和24時記時法中的時刻數是相同的。

生5：下午和晚上的24時記時法的時刻數都比普通記時法的時刻數大12時。

生6：1時～12時是鐘面的第一圈刻度；13時～24時是鐘面的第二圈刻度。

生7：24時記時法不能有時間詞語。如果有時間詞語，就表示是普通記時法。

生8：24時記時法改成普通記時法，要加上時間詞語。

生9：24時記時法改成普通記時法，下午和晚上的時刻數要減去12時。

……

多好的回答！在學生點點滴滴的感悟中，24時記時法和普通計時法的內在聯系已經厘清。可見，在處理教材時適當拓展教材意圖，努力讓知識間充滿邏輯聯系并讓學生感悟，就可能讓學生學到比較系統的數學知識，從而建構起邏輯性更強的知識結構，為后續教學提供方便。

總之，讓數學教學充滿邏輯的力量是由數學學科特點決定的，是實現數學教育目標與價值的根本途徑之所在，是數學教學方法之“大道”與“王道”。同時，讓數學教學充滿邏輯的力量也是培養學生邏輯思維能力的重要手段，可以為其他學科提供借鑒。【責任編輯：陳國慶】