基于入侵性雜草優化算法的有噪獨立分量分析方法
孔祥翠,王微微,陳靜靜,陳 宇
(中國石油大學(華東)信息與控制工程學院,山東 青島 266580)
0 引言
獨立分量分析(ICA)[1-2]作為有效的盲源分離[3]技術,是信號處理領域的熱點,在無線通訊、生物醫學[4]、圖像語音[5]、流型識別[6]、故障診斷[7]等領域應用廣泛.入侵性雜草優化(IWO)[8-10]算法是由 Mehrabian和Lucas受自然界雜草入侵農作物啟示提出來的一種新的優化智能算法.IWO算法簡單,易于實現,最大的優點是不需要遺傳操作算子,就可以簡單且有效地收斂到問題的全局最優解.
20世紀90年代,ICA理論得到較快發展[11-13],最具有代表性的是Fast ICA算法,穩定、快速的算法特性使得ICA技術實用化.此類算法大都假設無噪聲模型或把噪聲看作一個獨立信號,但在實際環境中,觀測信號往往摻雜各種各樣的噪聲,導致分離性能下降.Zhang H、Shi Z等利用信號的時序特性分離含噪信號,可以減小噪聲的影響,但信號時序特性不明顯時,分離效果較差[14-15].Hyvarinen A利用信號的非高斯特性,采用去偏技術對有噪ICA算法進行修正,減少由噪聲引起的偏差,適用性強[16].這些方法多采用梯度算法和牛頓法求解最優混合矩陣,容易陷入局部最優,很難獲得理想的分離結果.
文中算法以所有分離信號負熵和為目標函數,選用高斯密度函數估計負熵,簡化目標函數,保證穩定性,引入偏差去除技術對負熵進行去偏處理,以減少由噪聲引起的偏差,采用具有全局尋優性能的IWO算法估計混合矩陣;然后采用SVD-ICA算法得到源信號的無噪估計.
1 基于IWO的有噪ICA算法
1.1 有噪ICA模型
線性瞬時混合有噪ICA模型為

式中:x為觀測信號,x=[x1(t),x2(t),…,xM(t)]T;s為源信號,s=[s1(t),s2(t),…,sN(t)]T;t為時間;A為M×N維的混合矩陣,M=N;n為加性噪聲.
有噪ICA模型通常假設:(1)噪聲與源信號相互獨立;(2)噪聲n是高斯噪聲;(3)噪聲協方差矩陣Σ已知.
為了增強算法穩定性,需要對觀測信號進行魯棒白化處理[16],得到白化數據:

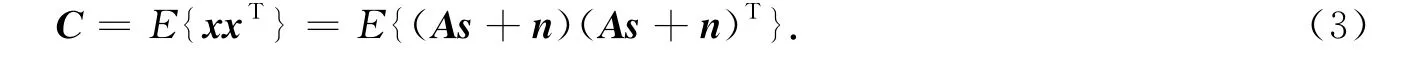
因為獨立分量s與噪聲n相互獨立,可得
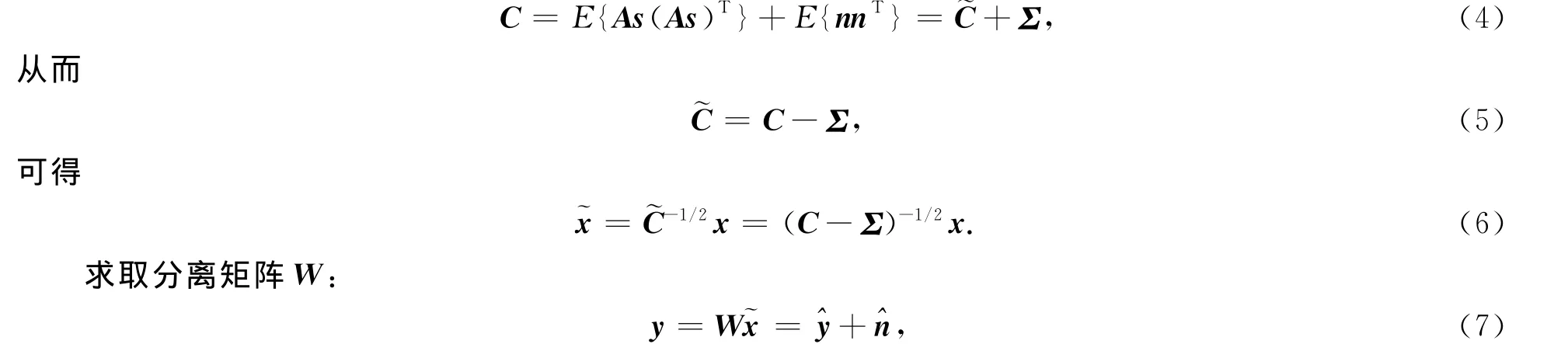
1.2 采用IWO算法優化的有噪ICA目標函數
入侵性雜草優化(Invasive Weed Optimization,IWO)算法模仿雜草入侵的種子空間擴散、占地生長、繁殖和競爭淘汰的基本過程,穩定性和自適應性較強.在IWO中,雜草表示問題產生的隨機可行解,種子是雜草的后代,種群是所有雜草的集合.算法中產生的子代按正態分布隨機分布于雙親周圍,種子在進化過程中早期和中期以較大步長分布于雜草空間,保持種群的多樣性,經過若干次迭代后,算法的種群個體競爭淘汰,適者生存.IWO算法具有良好的全局尋優性能,采用該算法對線性瞬時混合有噪ICA模型進行尋優.
根據中心極限定理[2]可知,信號越獨立,非高斯性越強.通常用負熵衡量信號的非高斯性,選用無噪分離信號的負熵作為目標函數:

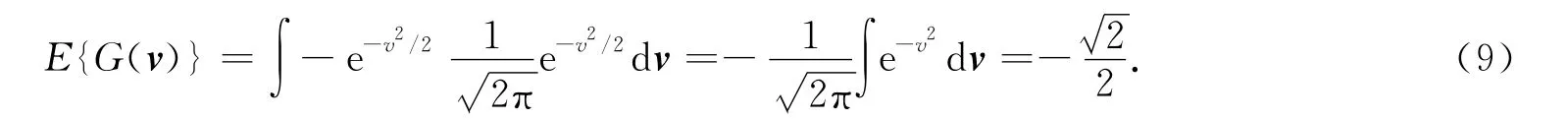
設z為任意非高斯隨機變量,n為方差為σ2的高斯噪聲變量[16],定義高斯函數φ,則對任意常數c>σ2,有


式中:ci與一一對應,di與+一一對應,di為第i個分量+對應下標d 的值.
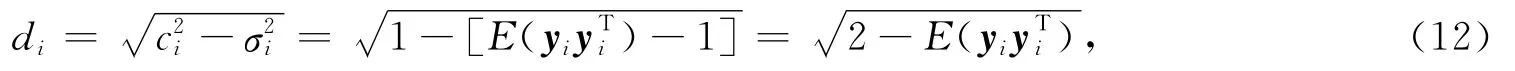
從而得到一個較為穩定的目標函數:
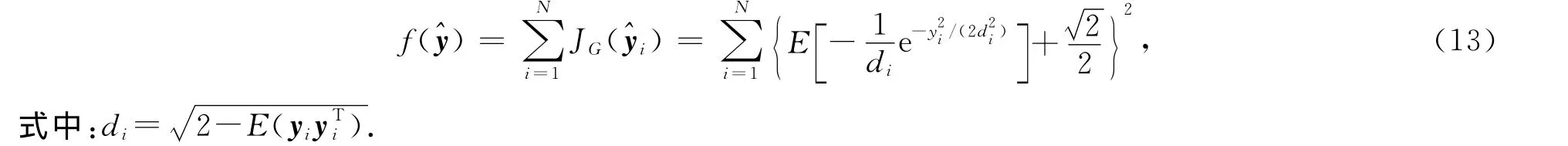
建立目標函數后,對目標函數進行優化.Fast ICA和Fast NoisyICA算法采用固定點算法對分離矩陣尋優,易陷入局部最優.文中采用具有全局尋優性能的IWO算法對分離矩陣W 尋優,并通過式(7)得到分離信號y.由于y中含有高斯噪聲,采用單路SVD-ICA方法[17]分離出無噪源信號估計基于IWO的有噪獨立分量分析算法流程見圖1.

2 仿真實驗
2.1 初始設置
以Mehrabian A R等[8]提出的參數作為變量初始值,應用2個亞高斯信號s1、s2和1個超高斯信號s3,分別對Fast ICA算法[13]、Fast NoisyICA算法[16]和文中算法進行仿真實驗.IWO變量初始值見表1.
仿真測試3路源信號均值為0,方差為1,采樣點數為8 000點;線性瞬時混合矩陣A為隨機生成:


表1 IWO變量初始值Table 1 IWO variables and the corresponding initial values
3路源信號從上至下分別為s1,s2和s3(見圖2).表達式分別為:s1=sin(2π×0.003t)、s2=sin(2π×0.01t)×sin(2π×0.000 7t)和s3=((rem(t/20,22)-11)/9)5,其中rem為求余運算.對源信號按式(1)進行混合,并且添加噪聲,得到有噪混合信號,信噪比為10dB(見圖3).

2.2 算法性能分析
Fast ICA算法、Fast NoisyICA算法和文中算法對信噪比為10dB的有噪混合信號分離結果見圖4.由圖4(a)和圖4(b)可以看出,Fast ICA和Fast NoisyICA算法對有噪混合信號的分離效果較差,分離信號中含有較多噪聲.由圖4(c)可看出,文中算法分離的信號與源信號除了在順序和幅度上不同外,波形基本一致,表明文中算法對源信號的估計較為準確.這是因為文中算法在估計負熵時,以高斯密度函數作為非線性函數,固定負熵中的不穩定項,增強算法的魯棒性,同時采用具有全局尋優性能的IWO算法,可較好地消除噪聲對源信號的影響.

采用獨立分量分析算法中常用的評價指標PI[1]衡量不同算法對有噪信號的分離性能:

式中:M為源信號個數;pij為位于矩陣P=W(C-Σ)-1/2A第i行第j列的元素.PI≥0,PI值越小,表示分離信號與源信號越相似,算法分離噪聲信號的性能越好.
采用相似因數[18]作為檢驗指標:

式中:T為采樣點數;β為相似因數,β越接近于1,表示分離效果越好,即分離信號與源信號的近似程度越高.
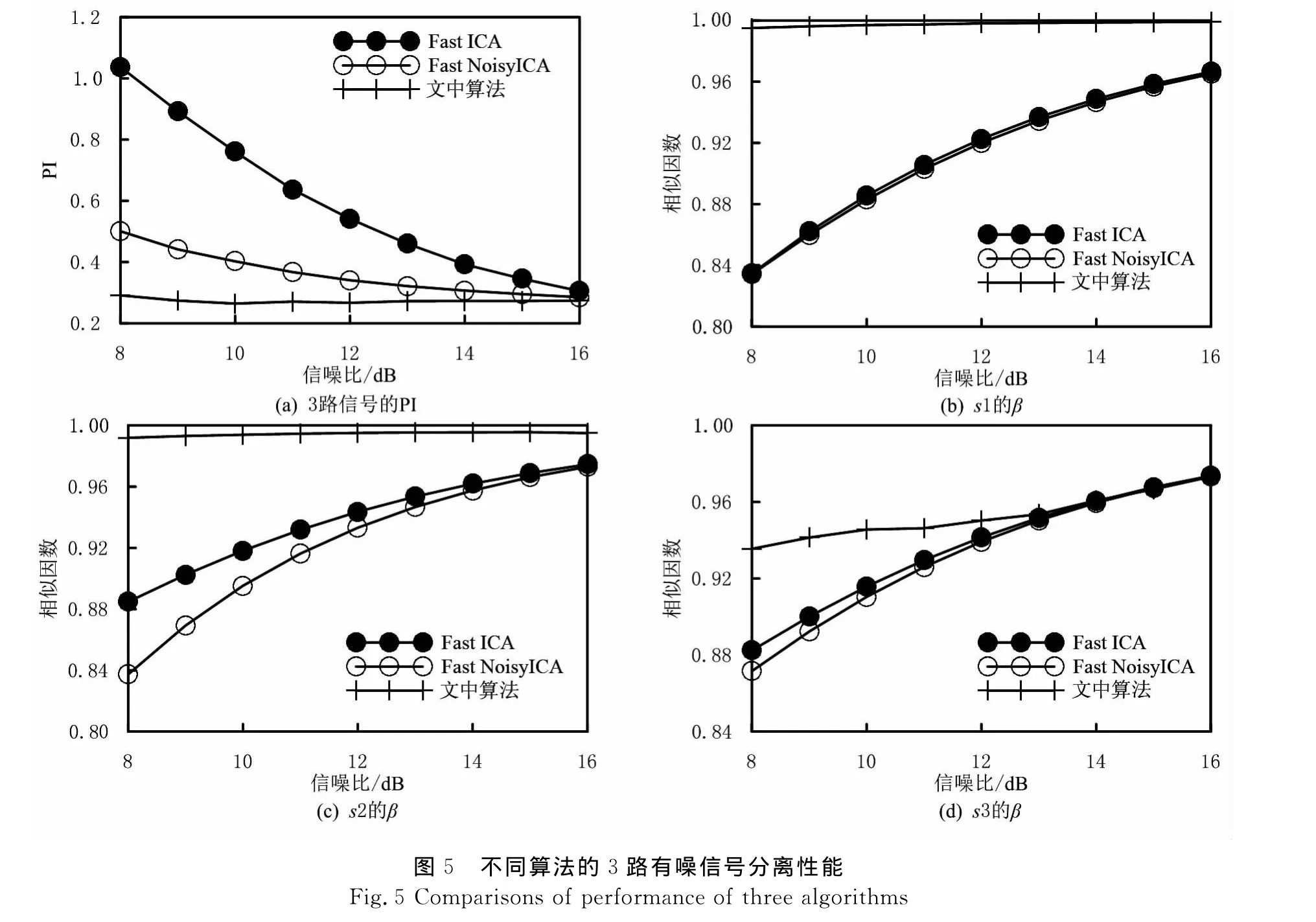
在信噪比為8~16dB時,不同算法對3路有噪信號分離性能見圖5(a).文中算法采用去偏處理,引入IWO算法尋優,減小由噪聲引起的影響,在較低信噪比下,文中算法的PI明顯小于其他2種算法的;在較高信噪比下,文中算法估計效果也優于其他2中算法的,文中算法同時消除目標函數中的不穩定項,使波動小、穩定性好.文中算法對混合矩陣的估計較為準確,對源信號波形恢復更好,由圖5(b)和圖5(c)可以看出:分離的前2路信號的相似因數要明顯大于其他2兩種算法的,并且比較接近于1;由圖5(d)可以看出:文中算法在較低信噪比下分離的第三路信號的相似因數大于其他2兩種算法的,隨著信噪比增加,相似因數逐漸增大.
為確保算法的穩定性和有效性,分別采用Fast ICA算法、Fast NoisyICA算法和文中算法進行30次仿真實驗,計算3種算法性能指標,比較最大、最小和平均值(見表2).由表2可以看出,文中算法的最大、最小和平均值明顯小于其他2種算法的,表明文中算法可以較精確地估計混合矩陣,分離精度較高.3種算法的相似因數見表3.由表3可以看出:文中算法的相似因數高于Fast ICA算法和Fast NoisyICA算法的,特別是第1路和第2路分離信號的相似因數明顯高于其他2種算法的,說明文中算法對源信號的估計更為準確.

表2 3種算法的PITable 2 PI values of three algorithms

表3 3種算法的相似因數Table 3 Similarities of three algorithms
3 結束語
提出基于IWO的有噪ICA算法,建立以分離信號負熵和為目標函數的優化模型,對目標函數去偏并修正不穩定項,保證目標函數的準確性和穩定性,采用的IWO尋優算法確保獲得全局最優分離矩陣.仿真實驗結果表明:文中算法有效地提高含噪聲情況下獨立分量分析算法的性能,與Fast ICA算法和Fast NoisyICA算法相比,該算法對混合矩陣估計更為精確,分離信號更接近源信號,是解決有噪獨立分量分析問題的一種有效算法.
(References):
[1]Hyv?rinen A,Karhunen J,Oja E.獨立成分分析[M].周宗潭,董國華,徐昕,等譯.北京:電子工業出版社,2007.Hyv?rinen A,Karhunen J,Oja E.Independent components analysis[M].Zhou Zongtan,Dong Guohua,Xu Xin,et al,trans.Beijing:Publishing House of Electronics Industry,2007.
[2]楊福生,洪波.獨立分量分析的原理與應用[M].北京:清華大學出版社,2006.Yang Fusheng,Hong Bo.The theory and application of independence component analysis[M].Beijing:Tsinghua University Press,2006.
[3]張發啟,張斌,張喜斌.盲信號處理及應用[M].西安:西安電子科技大學出版社,2006.Zhang Qifa,Zhang Bin,Zhang Xibin.Operation and application of blind signal[M].Xi'an:Xi'an University of Electronic Science and Technology Press,2006.
[4]LeVan P,Tyvaert L,Moeller F.Independent component analysis reveals dynamic ictal BOLD responses in EEG-fMRI data from focal epilepsy patients[J].Neuroimage,2010,49(1):366.
[5]李大輝,李長榮,楊陽.一種改進的瞬時混合語音信號盲分離算法[J].大慶石油學院學報,2007,31(4):80-83.Li Dahui,Li Changrong,Yang Yang.An improved algorithm for blind signal separation of instantaneous speech mixtures[J].Journal of Daqing Petroleum Institute,2007,31(4):80-83.
[6]周云龍,顧楊楊.基于獨立分量分析和RBF神經網絡的氣液兩相流流型識別[J].化工學報,2012,63(3):796-799.Zhou Yunlong,Gu Yangyang.Flow regime identification of gas/liquid two-phase flow based ICA and RBF neural networks[J].Ciesc Journal,2012,63(3):796-799.
[7]孟宗,梁智.基于EMMD和BSS的單通道旋轉機械故障診斷方法[J].儀器儀表學報,2013,34(3):635-642.Meng Zong,Liang Zhi.Fault diagnosis method for single channel rotating machinery based on EMMD and BSS[J].Chinese Journal of Scientific Instrument,2013,34(3):635-642.
[8]Mehrabian A R,Lucas C.A novel numerical optimization algorithm inspired from weed colonization [J].Ecological Informatics,2006,1(4):355-366.
[9]張氫,陳丹丹,秦仙蓉,等.雜草算法收斂性分析及其在工程中的應用[J].同濟大學學報:自然科學版,2010,38(11):1689-1693.Zhang Qing,Chen Dandan,Qin Xianrong,et al.Convergence analysis optimization algorithm in engineering of invasive weed and its application[J].Journal of Tongji University:Natural Science Edition,2010,38(11):1689-1693.
[10]Roy G G,Das S,Chakraborty P,et al.Design of non-uniform circular antenna arrays using a modified invasive weed optimization algorithm [J].Antennas and Propagation,IEEE Transactions on,2011,59(1):110-118.
[11]Yang H H,Amari S.Adaptive online learning algorithms for blind separation:maximum entropy and minimum mutual information[J].Neural Computation,1997,9(7):1457-1482.
[12]Cardoso J F,Laheld B H.Equivariant adaptive source separation[J].IEEE Transactions on Signal Processing,1996,44(12):3017-3030.
[13]Hyvarinen A.Fast and robust fixed-point algorithms for independent component analysis[J].IEEE Transactions on Neural Networks,1999,10(3):626-634.
[14]Zhang H,Shi Z,Guo C,et al.Blind source extraction for noisy mixtures by combining gaussian moments and generalized autocorrelations[J].Neural Processing Letters,2008,28(3):209-225.
[15]Shi Z,Tan X,Jiang Z,et al.Noisy blind source separation by nonlinear autocorrelation[C]//2010 3rd International Congress on Image and Signal Processing(CISP),2010:3152-3156.
[16]Hyvarinen A.Gaussian moments for noisy independent component analysis[J].IEEE Signal Processing Letters,1999,6(6):145-147.
[17]申永軍,楊紹普,孔德順.基于奇異值分解的欠定盲信號分離新方法及應用[J].機械工程學報,2009,45(8):64-70.Shen Yongjun,Yang Shaopu,Kong Deshun.New method of blind source separation in under-determined mixtures based on singular value decomposition and application[J].Journal of Mechanical Engineering,2009,45(8):64-70.
[18]成謝鋒,陶冶薇,張少白,等.獨立子波函數和小波分析在單路含噪信號盲分離中的應用研究:模型與關鍵技術[J].電子學報,2009,37(7):1522-1528.Cheng Xiefeng,Tao Yewei,Zhang Shaobai,et al.Applications of independent sub-band functions and wavelet analysis in singlechannel noisy signal BSS:model and crucial technique[J].Acta Electronic Signal,2009,37(7):1522-1528.

