風機葉片表面分離渦與寬頻噪聲輻射特性的分析

萬劍峰， 楊愛玲， 戴 韌

（1.上海理工大學 能源與動力工程學院，上海200093；2.河南理工大學 機械與動力工程學院，河南焦作454000）

風機葉輪的氣動噪聲包括離散噪聲和寬頻噪聲.離散噪聲來自于旋轉葉片周期性擊打氣流，它是以葉片通過頻率為基頻的氣動噪聲.寬頻噪聲主要來源于葉片表面的氣流壓力脈動.

葉片表面的氣流壓力脈動（聲源）主要來自3個部分：來流沖擊前緣的壓力脈動、尾緣渦脫落形成的壓力脈動［1］和葉片表面分離渦產生的壓力脈動［2］.Fukano等［3］建立了葉片表面附面層尾緣渦脫落引起的升力脈動的聲能量預測模型.Brooks［4］測量了3類聲源形成的噪聲，統計后建立了噪聲預測的半經驗公式.Tomimatsu等［5］和 Nakano等［6］通過實驗研究了不同葉型下攻角對分離渦產生的噪聲影響.居鴻賓等［7］通過實驗研究了風機的氣動聲場，得到寬頻噪聲來自于紊流邊界層和尾緣渦脫落，并分析了尾跡特性.Gaster［8］通過模擬和實驗發現，在低雷諾數（＜106）下，葉型表面出現分離，表面壓力脈動出現較大變化.

目前，對風機噪聲機理的研究基本源于對實驗結果的關聯分析，限于實驗能力，尚無能力得到流場結構與氣動噪聲的直接關聯.采用直接模擬（DNS）來計算氣動噪聲（CAA）在理論上是可行的，但是限于當今計算機條件，目前還難以實現.大渦模擬（LES）具有模擬大尺度分離渦流和非定常湍流的能力，成為當前研究氣動噪聲機理的基本途徑［9－10］.

如果計算流體力學軟件（CFD）能比較準確地模擬湍流的脈動與局部分離渦流，捕捉到形成氣動噪聲的壓力脈動源，了解每種聲源（脈動源）的特性，那么僅需要氣動設計即可達到很好的降噪效果.

筆者以常用的風機葉片Clark－Y葉型為模型，對葉片進行數值模擬來分析葉片表面分離渦的形成與發展規律，對比多種工況下葉片表面壓力脈動的特征及其所產生的聲壓指向圖和聲壓頻譜圖，分析葉型氣動聲源的遠場輻射能力，為設計風機時的氣動降噪提供思路.

1 流動和噪聲的數值模擬

1.1 流場計算

流場和聲場計算都采用Ansys V13.0軟件下的Fluent.流動模擬采用基于Smagorinsky模型的大渦模擬進行計算，其控制方程表示為［11－12］

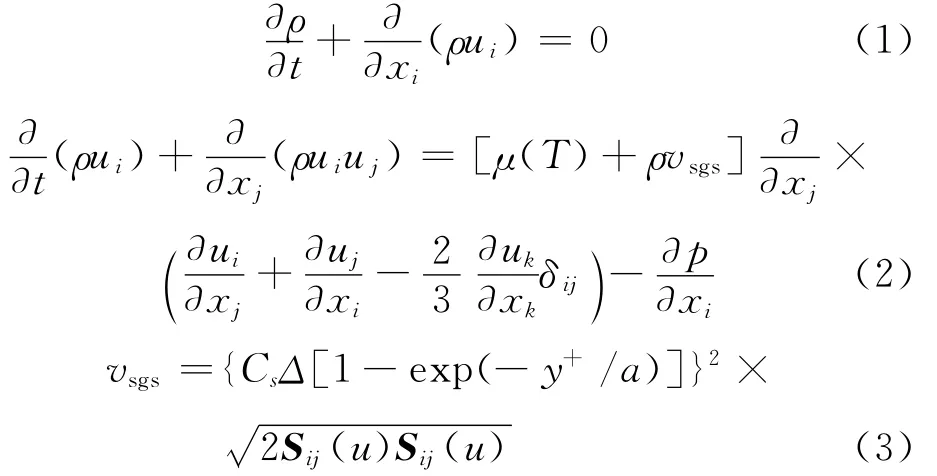
式中：ui、uj為過濾后的大尺度速度分量；μ（T）為動力黏度；l為密度；vsgs為亞格子渦黏系數；Sij為可解尺度的變形率張量；Δ為過濾尺度；Cs為模型常數，本模擬中取Cs＝1.0；δij為克羅內克符號；p 為靜壓；a為模型常數，a＝12.

為了加快LES的收斂速度，以定常RANS計算收斂值作為大渦模擬的初場.采用有限體積法離散方程，時間項離散采用二階隱式格式，對流項采用二階迎風格式，擴散項采用二階中心差分格式，壓力速度耦合迭代采用Simple算法.當數值計算的結果隨時間周期性變化時，認為LES計算收斂.

1.2 聲場計算

在遠場線性化假設和控制面為固壁邊界的條件下，由N－S方程可導出聲輻射FW－H方程：

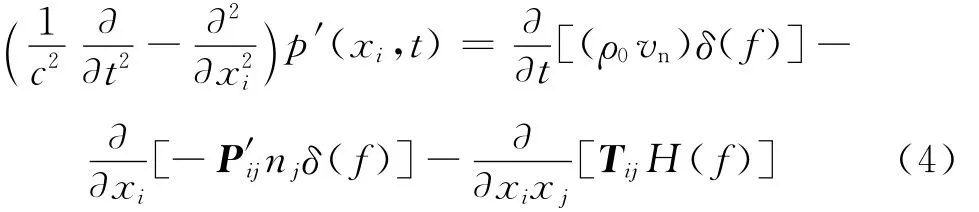
式中：c為當地聲速；p′（xi，t）為觀測點在t時刻的聲壓值；Pij為應力張量；vn為控制面法向速度；Tij為Lighthill張量；f為某一時刻的封閉控制面函數；H（f）為亥維賽德函數；下標0表示未擾動量，下標n表示在控制面外法向的方向，上標“’”表示擾動量.

式（4）等號右邊為聲源，依次表示單極子聲源、偶極子聲源和四極子聲源.在低馬赫數下，四極子聲源噪聲占總噪聲的比例低，且計算繁瑣，因此計算遠場聲壓時僅需考慮單極子聲源和偶極子聲源［13］.

1.3 計算方法的驗證

為了驗證計算方法的正確性，采用二維圓柱繞流模型［14］進行測算.圓柱直徑D為19mm，矩形計算區域為25D×11D，模型上游區域為5D，下游區域為19D.采用結構化分區劃分網格，邊界層第一層網格y＋＝1，在黏性底層內，主流區網格符合泰勒尺度［15］（λ≈（10vk／ε））.流體介質為溫度27℃的不可壓縮理想氣體，黏度μ＝1.789 4×10－5kg／（m·s）.

模擬值與實驗值的對比如表1所示.定義斯特勞哈爾數Sr＝fsD／u∞，其中fs表示渦脫落頻率.由表1可知，隨著流動Re的增大，Sr模擬值與實驗值的誤差逐步減小.考慮到風機葉片繞流的Re范圍為105～106，預計模擬的誤差可以控制在3%以下.

關于氣動噪聲方面的驗證，在Re＝9×104時測量點在距圓柱圓心35D、方位角度90°（尾流為0°，逆時針為正）處，總聲壓級的模擬值為115.12dB，實驗測量值［14］為117dB，誤差為1.6%.綜合流動和噪聲的測量結果可知，應用大渦模擬預測氣動噪聲的結果是可信的.

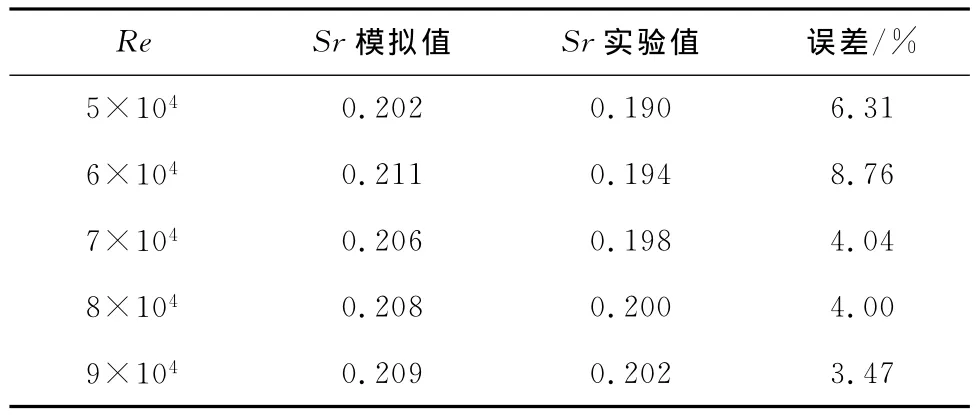
表1 斯特勞哈爾數Sr模擬值與實驗值的對比Tab.1 Comparison of Sr between simulated results and experimental data

2 計算結果與分析

2.1 計算模型

設定模型來流速度為100m／s，葉片弦長為0.06m，來流Re＝3.3×105.計算域為矩形區域，最遠來流（矩形區域入口邊）距前緣點8倍弦長，矩形區域出口邊距尾緣16倍弦長，壓力面和吸力面分別距另兩條邊5倍弦長.計算域外部邊界設置為速度遠場條件，葉型表面為無滑移邊界條件.流體介質為溫度27℃的不可壓縮理想氣體.

圖1給出了氣流方向、方位角以及葉片聲壓測點P的位置.A點為5°攻角下流動發生分離的分離點，C點為尾緣點，B點為A 點和C點之間的點，D點為5°攻角下前緣點，且A點、B點和C點在葉型的上表面，D點在葉型的下表面.

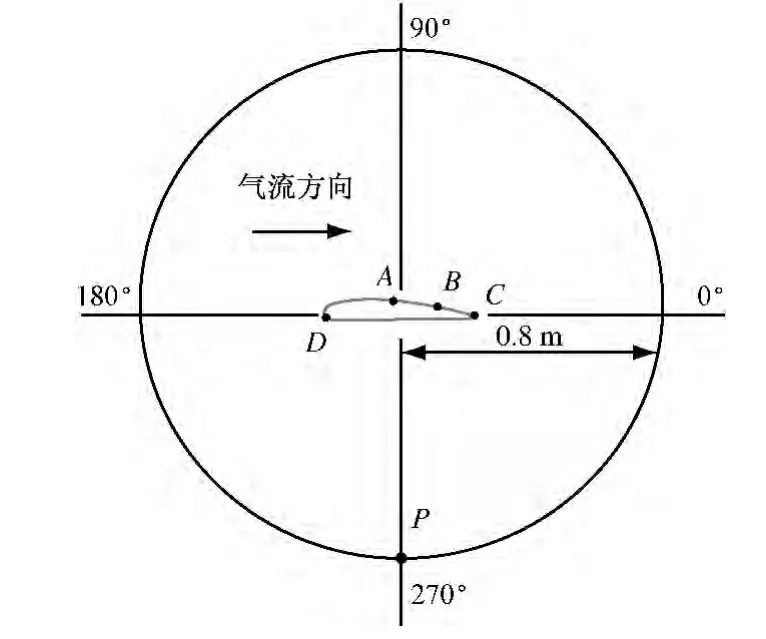
圖1 聲壓監測點位置Fig.1 Arrangement of sound pressure measuring points

2.2 網格無關性驗證

關于網格無關性驗證，采用表2中的3類網格，對5°攻角下Clark－Y葉型的流動進行計算.

圖2給出了穩態升力系數與尾緣點C點的瞬態壓力譜圖.升力系數實驗值為0.9，計算值與實驗值的最大誤差為4.4%，說明網格對穩態結果的影響小.但是圖2中，圖2（a）與圖2（b）差別很小且變化趨勢一致，圖2（c）與圖2（a）和圖2（b）的變化趨勢一致，但細節差異明顯.故網格種類1和網格種類2均可行，選取網格種類2進行計算.

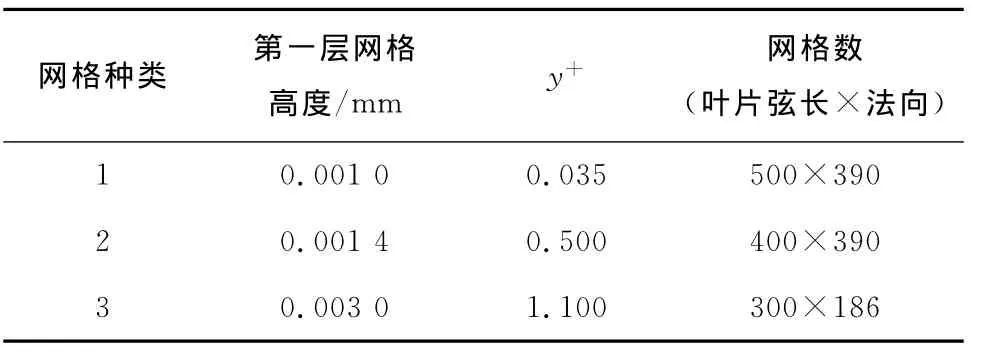
表2 網格無關性驗證Tab.2 Verification of grid independence

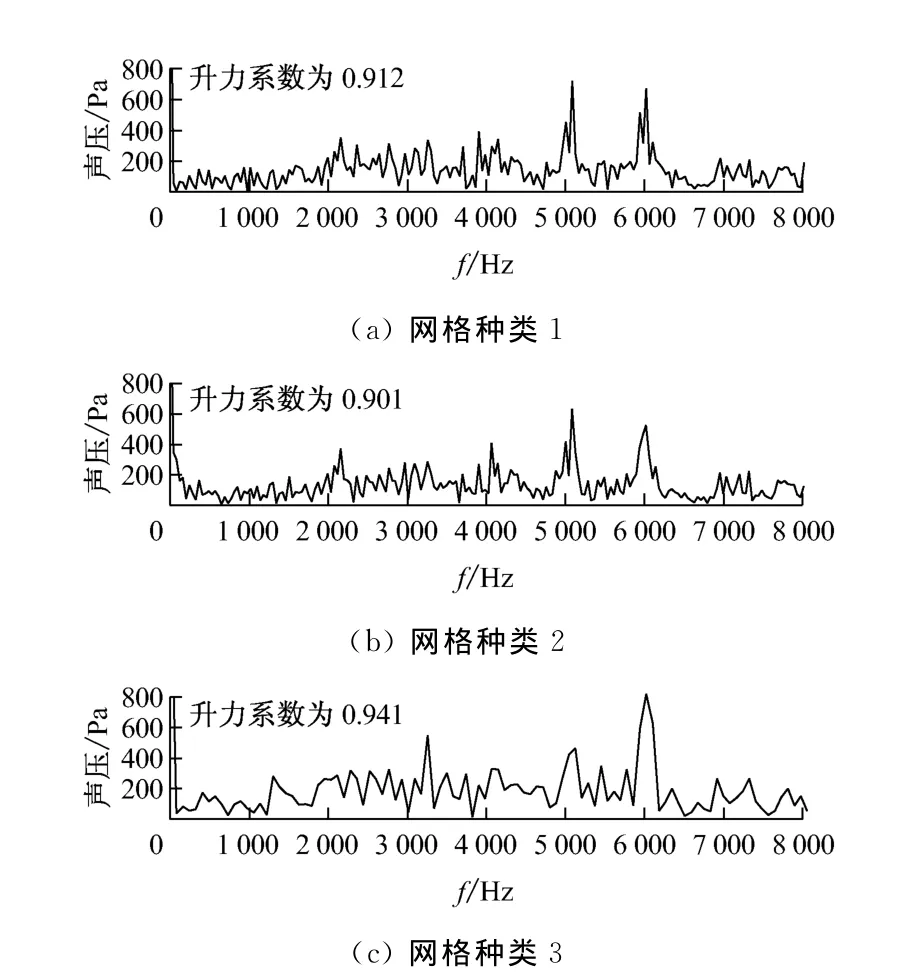
圖2 網格無關性驗證Fig.2 Verification of grid independence

2.3 葉片表面分離渦與壓力脈動的對應

圖3給出了8°攻角下，葉片吸力面的流動壓力和渦量分布圖，其中x，y為無量綱坐標，弦長定義為1.定義壓力系數Cp為

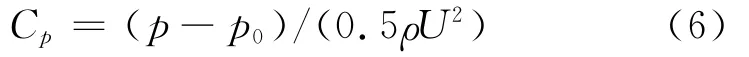
式中：p0為來流平均靜壓；U為來流平均速度.

在圖3中，第一個壓力波谷處（x＝0.18）分離點渦太小，在圖中較難分辨.尾緣處，分離渦已開始遠離葉片壁面，壓力波谷略偏離渦心位置.其他渦量集中的地方，葉片表面都會對應地產生一個波谷.隨著葉型表面各點分離渦的不斷“猝發”并從葉片表面脫落進入主流區，造成葉片表面各點持續的間歇性脈動.

圖4為8°攻角下流動速度流線圖.由圖4可知，葉片表面分離渦的流動速度要低于流體流動的速度，導致流體流動被分離渦阻礙.流體繞過分離渦時，流體速度提高，動壓上升，靜壓下降，使得分離渦處的葉片表面壓力下降.

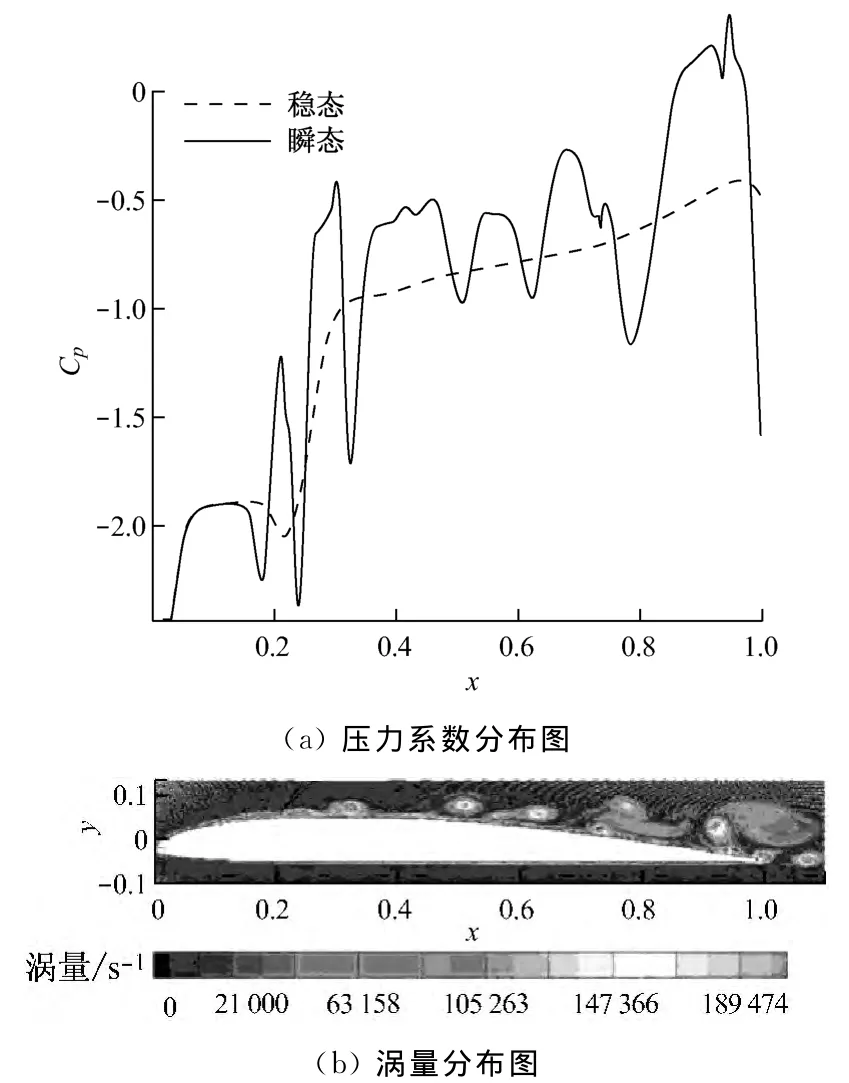
圖3 8°攻角下的吸力面壓力系數和渦量分布圖Fig.3 Pressure and vorticity distribution on suction surface at 8°angle of attack

圖4 8°攻角下的速度分布圖Fig.4 Velocity distribution at 8°angle of attack

2.4 不同攻角下的葉片表面壓力脈動

葉片表面氣流Cp的脈動值定義為

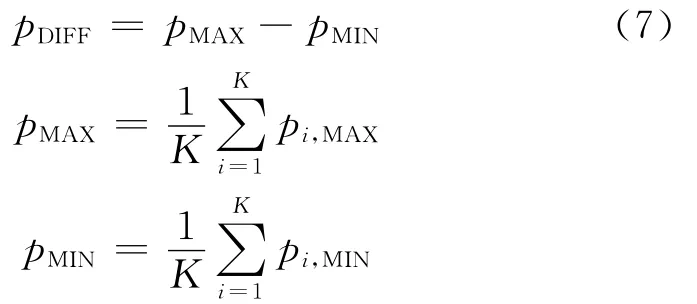
式中：pi，MAX和pi，MIN分別為某一Cp的極大值和極小值；K為極值個數.

圖5和圖6分別給出了5°攻角時，葉片吸力面和壓力面的pMEAN和脈動值分布，其中pMEAN為葉片表面每點對應的Cp時均值.由圖5和圖6可知，吸力面壓力脈動最大值處在分離點附近（x＝0.5）和葉片尾緣（x＝1），并且在分離點到尾緣之間的區域（0.5＜x＜1）都保持較大的壓力脈動.對于壓力面來說，尾緣（x＝1）壓力脈動大小相當于吸力面尾緣（x＝1）的壓力脈動，同時，在壓力面的前緣點（x＝0）也有一個較小的壓力脈動極值.

圖5 5°攻角時葉片吸力面的pMEAN和脈動值分布Fig.5 Profiles on blade suction surface at 5°angle of attack

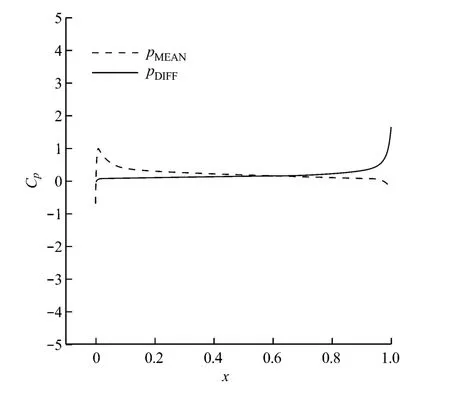
圖6 5°攻角時葉片壓力面的pMEAN和脈動值分布Fig.6 Profiles on blade pressure surface at 5°angle of attack

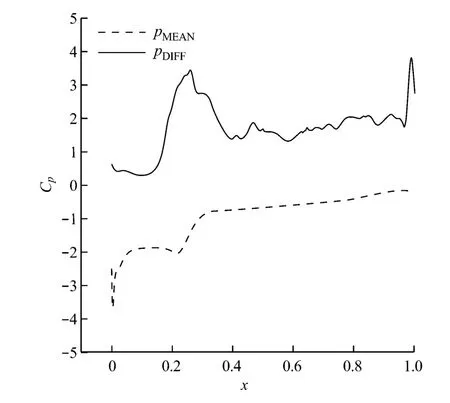
圖7 8°攻角時葉片吸力面的pMEAN和脈動值分布Fig.7 Profiles on blade suction surface at 8°angle of attack

圖7和圖8給出了8°攻角時，葉片吸力面和壓力面的pMEAN和脈動值分布.由圖7和圖8可知，在分離點附近和尾緣處壓力脈動極大，在它們之間的

區域壓力脈動較大，前緣點的壓力脈動極值比5°攻角時更大.

由以上模擬結果可以看出，葉型表面的壓力脈動（聲源）主要有3個：（1）前緣點的壓力脈動；（2）尾緣區的壓力脈動；（3）分離渦在吸力面產生的壓力脈動.從脈動幅值判斷，前2個的脈動強度相當，而第3個的脈動強度最低.

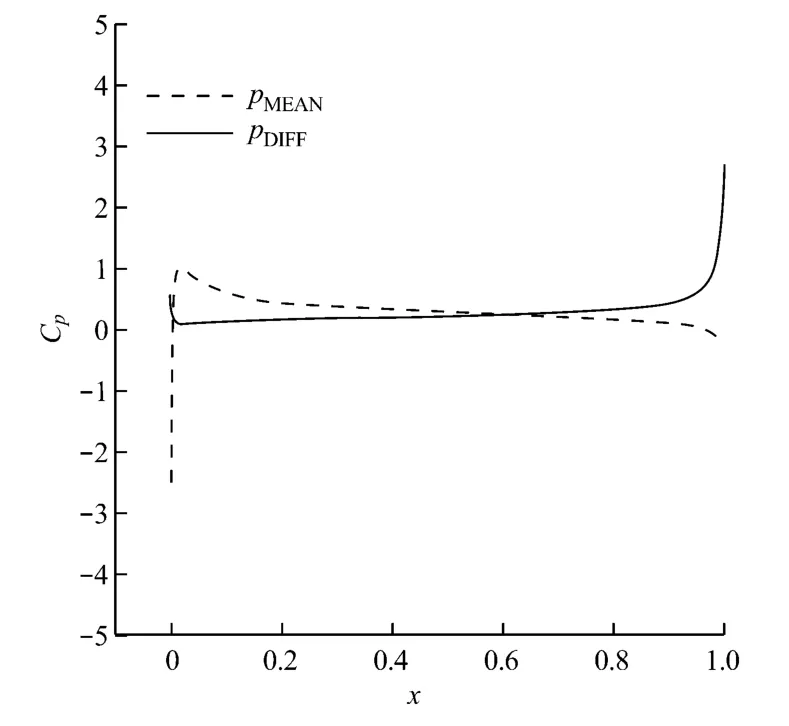
圖8 8°攻角時葉片壓力面的pMEAN和脈動值分布Fig.8 Profiles on blade pressure surface at 8°angle of attack

2.5 特征點壓力頻域分析

圖9給出了5°攻角時葉片表面3個點的壓力脈動頻譜域分布圖.從圖9可以看出，A點和B點在6 500Hz以上頻率時壓力仍有較大值（見圖9細線框），但C點卻沒有，故此特征由分離渦產生.其他兩處尖峰5 080Hz和6 100Hz（見圖9小圓圈），A點和B點來源于分離渦，C點來源于尾緣渦脫落，是共有特征.

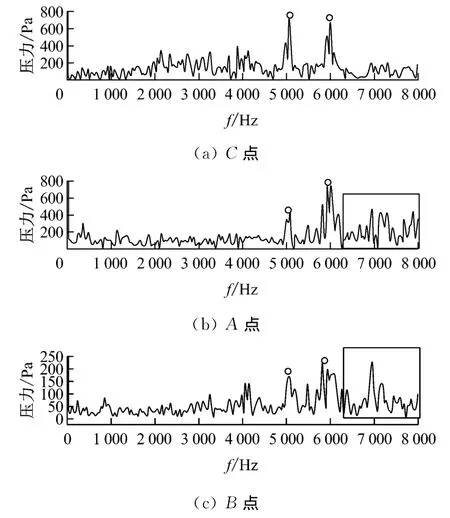
圖9 A點、B點和C點的壓力脈動頻域分布Fig.9 Pressure spectrums at points A，Band C

圖10給出了5°攻角時D點的壓力脈動頻域分布圖.從圖10可以看出，D點出現240Hz的尖峰（見圖10小圓圈），但吸力面的點（A點，B點和C點）卻沒有，故240Hz的尖峰是前緣點的特征.

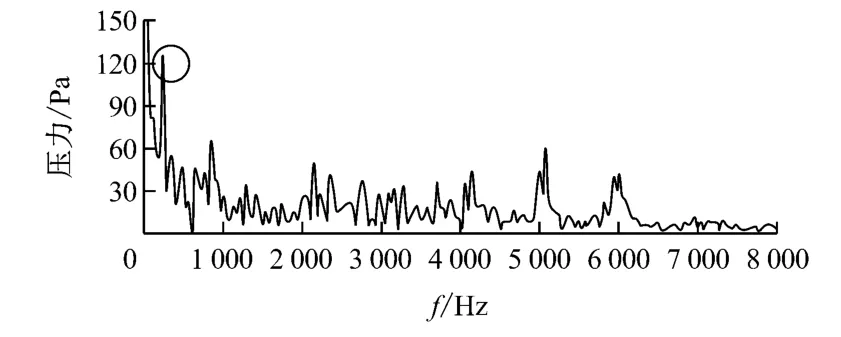
圖10 D點的壓力脈動頻域分布Fig.1 0 Pressure spectrums at point D

圖11給出了5°攻角時吸力面和壓力面分別對P點的聲壓頻域分布圖.由圖11可知，壓力面聲壓頻域分布有前緣點特征，注意到前緣點的壓力脈動要遠小于其他區域，可知前緣點的聲輻射能力最強；吸力面聲壓頻域分布圖僅有共有特征并無分離渦特征，故共有特征能產生較強的輻射；分離渦在6 500 Hz以上頻率的輻射能力低.

圖11 吸力面與壓力面的聲壓頻域分布（0.8m，270°）Fig.1 1 Spectrums of sound pressure on both suction and pressure surface（0.8m，270°）

2.6 表面聲源的輻射分析

圖12給出了在5°攻角、5 080Hz頻率下，在r／c＝13（r為接收點到葉片中心距離，c為弦長）處觀察到的聲壓指向圖.對比圖12的2個表面聲源聲壓指向圖，二者均有90°指向，不同的是壓力面還有140°和220°指向.對比兩表面的壓力脈動，二者均有尾緣的渦脫落壓力脈動，不同的是吸力面有分離渦脈動，壓力面有前緣脈動.相同部分脈動產生了90°指向，不同部分前緣脈動產生了140°和220°指向，另外分離渦脈動卻沒有產生明顯特征.故分離渦的共有特征為聲輻射能力低于前緣和尾緣壓力脈動的聲輻射能力.

綜上所述，前緣點壓力脈動非常集中，幾乎是一個前緣壁面上的點聲源.尾緣區壓力脈動都是源于同一渦脫落，各點壓力脈動相位差小.分離渦產生的壓力脈動雖大，但各點相位都不同.因此，前緣點壓力脈動聲輻射能力最強，而相位差小、分布區域小的尾緣壓力脈動聲輻射能力次之，分布區域大、各點相位差大的分離渦產生的壓力脈動聲輻射能力最低.

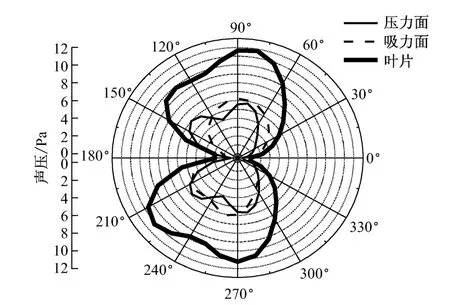
圖12 13倍弦長處的聲壓指向圖Fig.1 2 Sound pressure direction diagram at 13times the chord length

3 結 論

（1）在小攻角葉型發生分離時，分離渦沿葉片表面形成渦束，在分離渦與葉片表面的接觸處形成表面壓力低谷，這些表面壓力脈動形成了流動寬頻噪聲的一個新聲源.

（2）葉片寬頻噪聲的3個來源中，前緣點的壓力脈動聲輻射能力最強，尾緣區壓力脈動聲輻射能力次之，葉片表面的渦流產生的壓力脈動最大，但其聲輻射能力最低.寬頻噪聲主要來源于前緣點壓力脈動和尾緣區壓力脈動，控制前緣噪聲與尾緣邊界層脫落噪聲，對風機的降噪設計更有意義.

［1］YANG Zhiyin，VOKE P R.Large－eddy simulation of boundary－layer separation and transition at a change of surface curvature［J］.Journal of Fluid Mechanics，2001，439：305－333.

［2］LIN J C M，PAULEY L L.Low－reynolds－number separation on an airfoil［J］.AIAA Journal，1996，34（8）：1570－1577.

［3］FUKANO T，KODAMA Y，SENOO Y.Noise generated by low pressure axial flow fans，I：modeling of the turbulent noise［J］.Journal of Sound and Vibration，1977，50（1）：63－74.

［4］BROOKS T F，POPE D S，MARCOLINI M A.Airfoil self－noise prediction［M］.Washington DC，USA：NASA，1989：36－45.

［5］TOMIMATSU S，FUJISAWA N.Measurement of aerodynamic noise and unsteady flow field around a symmetrical airfoil［J］.Journal of Visualization，2002，5（4）：381－388.

［6］NAKANO T，FUJISAWA N，OGUMA Y，et al.Experimental study on flow and noise characteristics of NACA0018airfoil［J］.Journal of Wind Engineering and Industrial Aerodynamics，2007，95（7）：511－531.

［7］居鴻賓，鐘芳源.風機氣動聲場及其相似性實驗研究［J］.流體機械，1995，23（7）：3－6.JU Hongbin，ZHONG Fangyuan.Experiment study on fans＇aerodynamic sound field and its similarity［J］.Fluid Machinery，1995，23（7）：3－6.

［8］GASTER M.The structure and behavior of laminar separation bubble［M］.London，UK：AGARD CP－4，1969.

［9］傅慧萍，繆國平.大渦模擬在噪聲計算中的應用［J］.上海交通大學學報，2009，43（8）：1307－1311.FU Huiping，MIAO Guoping.Application of LES method to flow noise calculation［J］.Journal of Shanghai Jiaotong University，2009，43（8）：1307－1311.

［10］卓文濤，季锃釧，陳二云，等.翼型氣動性能與噪聲的綜合優化設計方法［J］.動力工程學報，2012，32（6）：481－486.ZHUO Wentao，JI Zengchuan，CHEN Eryun，et al.Comprehensive optimization on aerodynamic and aeroacoustic performance of airfoils［J］.Journal of Chinese Society of Power Engineering，2012，32（6）：481－486.

［11］LARCHEVêQUE L，SAGAUT P，MARY I，et al.Large－eddy simulation of a compressible flow past a deep cavity［J］.Physics of Fluids，2003，15（1）：193－211.

［12］LENORMAND E，SAGAUT P，COMTE P，et al.Subgrid－scale models for large－eddy simulations of compressible wall bounded flows［J］.AIAA Journal，2000，38（8）：1340－1350.

［13］CURLE N.The influence of solid boundaries upon aerodynamic sound［J］.Proceedings of the Royal Society，1955，231（1187）：505－514.

［14］REVELL J D，PRYZD R A，HAYS P A.Experimental study of airframe noise vs.drag relationship for circular cylinders［R］.Washington DC，USA：NASA，1977：120－122.

［15］張兆順，崔桂香，許曉陽.湍流大渦數值模擬的理論和應用［M］.北京：清華大學出版社，2008：118.