帶有p-Laplacian算子的分?jǐn)?shù)階多點(diǎn)邊值問(wèn)題單調(diào)正解的存在性

張 瑜，侯成敏

（延邊大學(xué)數(shù)學(xué)系，吉林延吉 133002）

帶有p-Laplacian算子的分?jǐn)?shù)階多點(diǎn)邊值問(wèn)題單調(diào)正解的存在性

張 瑜，侯成敏

（延邊大學(xué)數(shù)學(xué)系，吉林延吉 133002）

考慮一類(lèi)帶有p-Laplacian算子的分?jǐn)?shù)階多點(diǎn)邊值問(wèn)題.首先，通過(guò)變換將分?jǐn)?shù)階多點(diǎn)邊值問(wèn)題轉(zhuǎn)化為整數(shù)階差分方程多點(diǎn)邊值問(wèn)題；其次，利用方程及其邊界條件得到表達(dá)式及一些性質(zhì)；最后，利用單調(diào)迭代方法研究變換后的方程，得到原方程非增正解的存在性.

分?jǐn)?shù)階差分方程；多點(diǎn)邊值問(wèn)題；正解的存在性；單調(diào)迭代

0 引言

整數(shù)階差分方程包括帶有p-Laplacian算子的整數(shù)階差分方程，已廣泛應(yīng)用于計(jì)算機(jī)信息控制、工程控制、神經(jīng)網(wǎng)絡(luò)等領(lǐng)域中，受到眾多學(xué)者的關(guān)注并得到許多結(jié)果[1-7].如苑成軍等[3]通過(guò)不動(dòng)點(diǎn)定理研究奇異四階p-Laplacian差分方程邊值正解的存在惟一性；Candito P等[4]利用臨界點(diǎn)定理研究帶有p-Laplacian算子的兩點(diǎn)邊值問(wèn)題正解的存在；Kuang J H[5]和Gao Chenghua分別利用臨界點(diǎn)定理研究帶有p-Laplacian算子離散邊值問(wèn)題解的存在性.這些研究結(jié)果是對(duì)整數(shù)階差分方程給出的，而帶有p-Laplacian算子的分?jǐn)?shù)階差分方程的研究成果相對(duì)較少，如李寶玲等[8]利用變分法和帶有強(qiáng)制條件的臨界點(diǎn)定理，研究一類(lèi)帶有p-Laplacian算子的分?jǐn)?shù)階差分方程邊值問(wèn)題至少有3個(gè)解的存在性；Lv Weidong[9]利用不動(dòng)點(diǎn)定理研究帶有p-Laplacian算子的離散分?jǐn)?shù)階解的存在性；He Yansheng等[10]利用臨界點(diǎn)定理研究帶有p-Laplacian算子的離散分?jǐn)?shù)階邊值問(wèn)題解的存在性.利用單調(diào)迭代方法研究帶有p-Laplacian算子的分?jǐn)?shù)階多點(diǎn)邊值問(wèn)題單調(diào)正解的存在性少見(jiàn)，筆者考慮帶有p-Laplacian算子的分?jǐn)?shù)階多點(diǎn)邊值問(wèn)題（簡(jiǎn)稱(chēng)FBVP），即

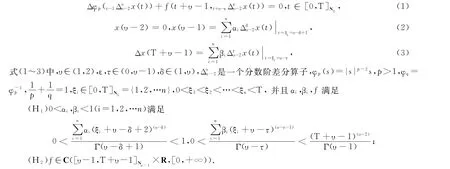
通過(guò)變換y（t）=Δυ-1υ-2x（t）把原問(wèn)題轉(zhuǎn)化為整數(shù)階差分方程邊值問(wèn)題，利用單調(diào)迭代方法證明轉(zhuǎn)化后的方程存在2個(gè)非增正解，從而得到原方程存在2個(gè)非增正解.

1 預(yù)備知識(shí)

2 主要結(jié)果

由Arzela-Ascoli定理可知QΩ是相對(duì)緊的，即Q是緊的.

最后，證明在[υ-1，T+υ-1]Nυ-1火R上，若f（s+υ-1，·）關(guān)于第二個(gè)變量是非減的，對(duì)任意yi∈P（i =1，2）且y1＞y2.設(shè)Ayi（i=1，2）關(guān)于yi（i=1，2）是滿足式（9）的2個(gè)常數(shù)，由引理2.3得Ay1≤Ay2.在通過(guò)Qy的定義，易證Qy1＞Qy2.證畢.

3 解的存在性

4 結(jié)束語(yǔ)

單調(diào)迭代方法是研究整數(shù)階差分方程邊值問(wèn)題及分?jǐn)?shù)階微分方程邊值問(wèn)題的有效方法之一，在研究分?jǐn)?shù)階差分方程邊值問(wèn)題中還沒(méi)有被應(yīng)用.文中首次采用單調(diào)迭代方法研究一類(lèi)帶有p-Laplacian算子的分?jǐn)?shù)階多點(diǎn)邊值問(wèn)題單調(diào)正解的存在性，因此結(jié)果具有一定創(chuàng)新意義.

[1] Goodrich C S.Existence and uniqueness of solutions to a fractional difference equation with nonlocal conditions[J].Comput Math Appl，2011，61（2）：191-202.

[2] Holm M T.The theory of Discrete fractional calculus：Development and application[D].Lincoln：University of Nebraska，2011：5-32.

[3] 苑成軍，文香丹，孟慶元.奇異四階p-Lapacian差分方程邊值正解的存在惟一性[J].東北師大學(xué)報(bào)：自然科學(xué)版，2010，42（1）：5-9.

Yuan Chengiun，Wen Xiangdan，Meng Qinyuan.Existence and uniqueness of positive solutions of difference equation boundary value with singular four order p-Lapacian[J].Journal of Northeast Normal University：Natural Science Edition，2010，42（1）：5-9

[4] Candito P，Giovannelli N.Multiple solutions for adiscrete boundary value problem involving the p-Laplacian[J].Comput Math Appl， 2008（56）：959-964.

[5] Kuang J H.Existence of homoclinic solutions for higher-order periodic difference equations with p-Laplacian[J].J.Math.Anal.Appl，2014（417）：904-917.

[6] Gao Chenghua.Solutions to discrete multiparameter periodic boundary value problems involving the p-Laplacian via critical point theory[J].Acta Mathematica Scientia：English Series，2014，34（4）：1225-1236.

[7] Parka J H，Chung S Y.Positive solutions for discrete boundary value problems involving the p-Laplacian with potential terms[J]. Comput Math Appl，2011（61）：17-29.

[8] 李寶玲，葛琦.一類(lèi)帶有p-Laplacian算子的分?jǐn)?shù)階差分方程的多重解[J].延邊大學(xué)學(xué)報(bào)：自然科學(xué)版，2014，114（2）：104-108. Li Baoling，Ge Qi.Multiple solutions for a class offractional difference equations involving the p-Laplacian operator[J].Journal of Yanbian University：Natural Science Edition，2014，114（2）：104-108.

[9] Lv Weidong.Existence of solutions for discrete fractional boundary value problems with a p-Laplacian operator[J].Advances in Difference Equations，2012，163：1-10.

[10] He Yansheng，Chengmin Hou.Existence of solutions for discrete fractional boundary value problems with p-Laplacian operator[J]. Journal of Mathematical Research with Applications，2014，34（2）：197-208.

O175.7

A

2095-4107（2014）06-0116-11

DOI 10.3969/i.issn.2095-4107.2014.06.015

2014-10-09；編輯：關(guān)開(kāi)澄

國(guó)家自然科學(xué)基金項(xiàng)目（11161049）

張 瑜（1989-），女，碩士研究生，主要從事微分方程理論及其應(yīng)用方面的研究.

侯成敏，E-mail：cmhou@foxmail.com