水平井“多段分簇”壓裂簇間干擾的數(shù)值模擬

潘林華 張士誠(chéng) 程禮軍 陸朝暉 柳凱譽(yù)

1.國(guó)土資源部頁(yè)巖氣資源勘查重點(diǎn)實(shí)驗(yàn)室·重慶地質(zhì)礦產(chǎn)研究院

2.重慶市頁(yè)巖氣資源與勘查工程技術(shù)研究中心·重慶地質(zhì)礦產(chǎn)研究院

3.油氣資源與探測(cè)國(guó)家重點(diǎn)實(shí)驗(yàn)室·重慶頁(yè)巖氣研究中心

4.中國(guó)石油大學(xué)（北京）石油工程學(xué)院 5.中國(guó)石油長(zhǎng)城鉆探公司井下作業(yè)分公司

水平井分段壓裂已經(jīng)成為低滲透油氣藏開(kāi)發(fā)的關(guān)鍵技術(shù)［1］，常規(guī)水平井壓裂一般采用單簇射孔、多段壓裂的施工模式，形成的壓裂裂縫體積有限。國(guó)內(nèi)外學(xué)者在常規(guī)的水平井壓裂的基礎(chǔ)上，對(duì)壓裂工具和壓裂工藝進(jìn)行改進(jìn)，形成了水平井“多段分簇”壓裂方法，每個(gè)壓裂段射多簇孔，每段能形成多條壓裂裂縫，這樣能盡可能增加改造體積［2－4］，保證低滲透油氣藏和非常規(guī)油氣藏的壓裂增產(chǎn)效果。

水平井分段壓裂方面，目前主要集中在壓裂裂縫條數(shù)、裂縫長(zhǎng)度和裂縫間距對(duì)水平井產(chǎn)能的影響［5－10］。但是，在水平井“多段分簇”壓裂過(guò)程中，壓裂裂縫間的相互干擾是一個(gè)無(wú)法回避的問(wèn)題，裂縫干擾的存在可能導(dǎo)致中間的射孔簇?zé)o法形成有效的壓裂裂縫［11－13］。

筆者基于流—固耦合的基本方程和損傷力學(xué)原理，建立了水平井“多段分簇”壓裂的三維有限元模型，利用該模型研究了儲(chǔ)層物性、施工參數(shù)、射孔簇?cái)?shù)等對(duì)水平井“多段分簇”壓裂裂縫干擾的影響。利用所建立的模型對(duì)西南某區(qū)塊的一口水平井進(jìn)行了壓裂設(shè)計(jì)優(yōu)化，優(yōu)化后壓裂井的產(chǎn)量增加明顯，表明本模型對(duì)現(xiàn)場(chǎng)壓裂具有指導(dǎo)和借鑒意義。

1 水平井“多段分簇”壓裂裂縫擴(kuò)展數(shù)學(xué)模型

水平井“多段分簇”壓裂，從力學(xué)方面分析，可以分成以下3個(gè)流場(chǎng)［13］：①液體流場(chǎng)——壓裂液在裂縫中的流動(dòng)，對(duì)裂縫面產(chǎn)生應(yīng)力、應(yīng)變的影響；②巖石應(yīng)力場(chǎng)——儲(chǔ)層基質(zhì)承受一定的應(yīng)力并產(chǎn)生應(yīng)變；③孔隙中滲流場(chǎng)——孔隙中充滿流體，在壓裂過(guò)程中會(huì)發(fā)生流動(dòng)和交換，反過(guò)來(lái)會(huì)影響儲(chǔ)層基質(zhì)的應(yīng)力和應(yīng)變。水平井“多段分簇”壓裂裂縫干擾主要通過(guò)這3個(gè)流場(chǎng)的變化而產(chǎn)生。

1.1 流—固耦合基本方程

儲(chǔ)層基質(zhì)的應(yīng)力遵循有效應(yīng)力原理為：

根據(jù)虛功原理，壓裂儲(chǔ)層巖石的平衡方程為［14］：

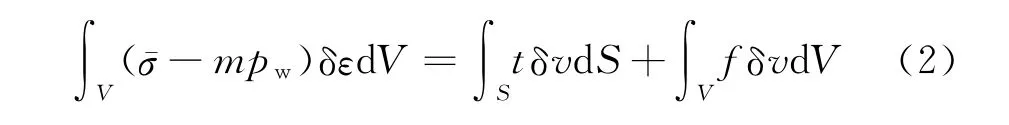
式中δε為儲(chǔ)層基質(zhì)的虛應(yīng)變率，s－1；t為單元面載荷，N／m2；δv為儲(chǔ)層基質(zhì)的虛運(yùn)動(dòng)速度，m／s；f為體力載荷，N／m3；dS為面載荷的作用面積，m2；dV 為計(jì)算單元的體積，m3。

根據(jù)流體質(zhì)量守恒原理，流體介質(zhì)的連續(xù)性方程為［14］：

式中J為儲(chǔ)層孔隙的體積改變率，無(wú)因次；nw為孔隙中液體體積與儲(chǔ)層總體積的比值，無(wú)因次；ρw為儲(chǔ)層液體密度，kg／m3；x為液體流動(dòng)的方向向量，m；dt為時(shí)間步，s；vw為儲(chǔ)層液體的流動(dòng)速度，m／s。

孔隙液體流動(dòng)速度的計(jì)算公式為［15］：

式中a為單位轉(zhuǎn)換常量；g為重力加速度，m／s2；μ為孔隙液體黏度，Pa·s；K 為儲(chǔ)層的動(dòng)態(tài)滲透率，mD；pw為儲(chǔ)層孔隙壓力增量，Pa。

儲(chǔ)層的孔隙壓力和應(yīng)力相互耦合，儲(chǔ)層孔隙壓力和有效應(yīng)力的變化對(duì)孔隙度和滲透率產(chǎn)生影響。本計(jì)算模型中，孔隙度和滲透率在計(jì)算過(guò)程中動(dòng)態(tài)變化，變化方式如下所示［16］：

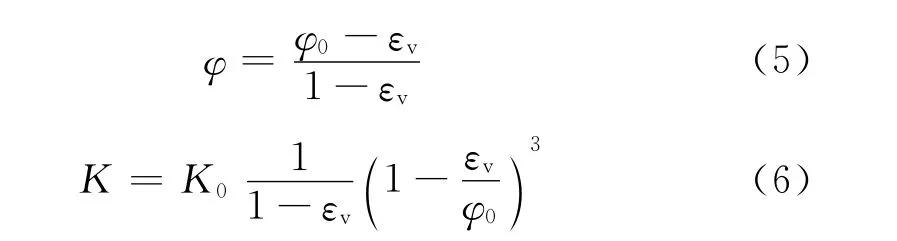
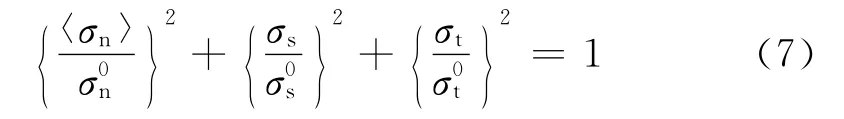
式中σn為垂直于黏結(jié)單元的法向應(yīng)力，Pa；符號(hào)〈〉表示黏結(jié)單元不抗壓；σs、σt分別為平行于黏結(jié)單元的兩個(gè)切向應(yīng)力，Pa；σ0n為黏結(jié)單元的法向損傷極值，Pa；σ0s、σ0t分別為黏結(jié)單元的切向損傷的極值，Pa。

裂縫擴(kuò)展過(guò)程中，裂縫擴(kuò)展造成黏結(jié)單元的損傷采用彈性模量線性退化準(zhǔn)則：

式中E0為儲(chǔ)層的初始彈性模量，Pa；E為儲(chǔ)層的動(dòng)態(tài)彈性模量，Pa；d為裂縫擴(kuò)展造成的損傷因子，無(wú)因次，根據(jù)裂縫的位移計(jì)算獲得。

式中φ為儲(chǔ)層的動(dòng)態(tài)孔隙度，無(wú)因次；φ0為儲(chǔ)層的初始孔隙度，無(wú)因次；εv為計(jì)算單元的體積應(yīng)變，無(wú)因次；K0為巖石的初始滲透率，mD。

1.2 裂縫擴(kuò)展模型

采用零厚度黏結(jié)單元模擬水平井“多段分簇”壓裂的裂縫擴(kuò)展過(guò)程，利用黏結(jié)單元的損傷表征壓裂裂縫擴(kuò)展。

根據(jù)張應(yīng)力和剪切應(yīng)力的復(fù)合判斷準(zhǔn)則評(píng)價(jià)裂縫的起裂、擴(kuò)展，判斷準(zhǔn)則為［17］：

式中Qt為黏結(jié)單元切向流量，m3／s；topen為張開(kāi)位移，m；Δp為黏結(jié)單元間的壓差，Pa。

壓裂液沿黏結(jié)單元表面的法向流量［19］：

式中Qn為黏結(jié)單元的法向流量，m3／s；cn為壓裂液的濾失系數(shù)，m3／（Pa·s）；pb為黏結(jié)單元相鄰的基質(zhì)單元的孔隙壓力，Pa；pi為黏結(jié)單元流壓，Pa。

模擬過(guò)程中，將混合支撐劑和壓裂液的攜砂液等效為一種流體，液體等效黏度與支撐劑濃度關(guān)系為［20］：

壓裂液流動(dòng)分解為切向流動(dòng)和法向流動(dòng)。壓裂液沿水力裂縫單元切向流動(dòng)的計(jì)算公式為［18］：

式中μ為等效后的液體的黏度，Pa·s；μ0為無(wú)支撐劑的液體黏度，Pa·s；c為攜砂液中支撐劑的體積濃度，無(wú)因次。

2 水平井“多段分簇”壓裂裂縫擴(kuò)展計(jì)算模型

根據(jù)西南某地區(qū)的部分壓裂井的微地震監(jiān)測(cè)和測(cè)井解釋結(jié)果，發(fā)現(xiàn)該區(qū)塊的天然裂縫不發(fā)育，壓裂過(guò)程中，壓裂裂縫以平面裂縫為主，因此，本計(jì)算模型假設(shè)壓裂裂縫為平面縫。

所建立的計(jì)算模型示意圖如圖1所示，計(jì)算模型的總厚度為60.0m，壓裂目的層厚度為40.0m，上下隔層的厚度為10.0m，計(jì)算模型的寬度為200.0m，長(zhǎng)度（壓裂裂縫長(zhǎng)度方向）為300.0m。

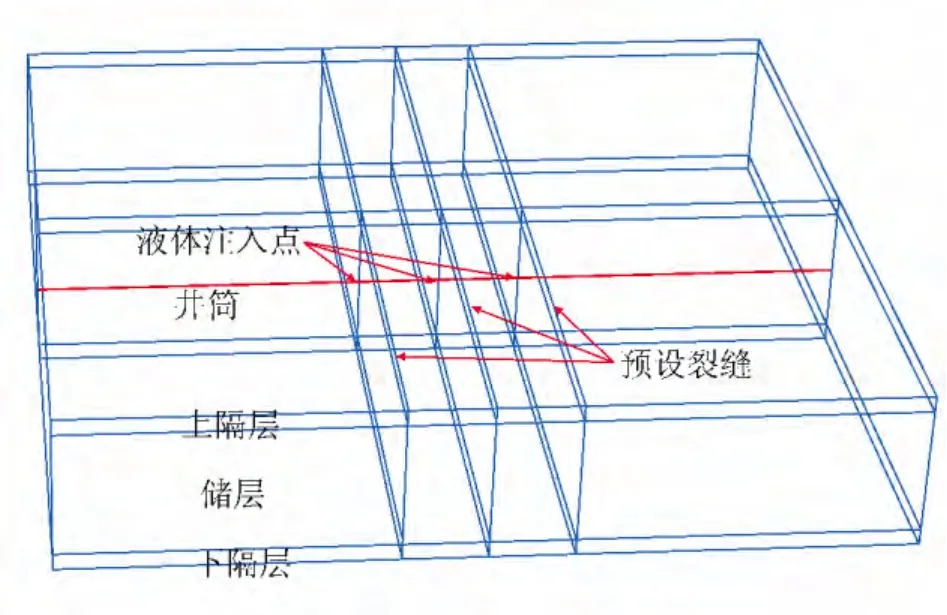
圖1 水平井“分段多簇”射孔壓裂計(jì)算模型示意圖

計(jì)算模型的參數(shù)如表1所示，計(jì)算模型主要包括巖石力學(xué)、孔隙度、滲透率、地應(yīng)力、壓裂液黏度、施工排量等參數(shù)。為了研究某些參數(shù)對(duì)裂縫干擾的影響，部分參數(shù)可能會(huì)發(fā)生改變。

表1 計(jì)算模型參數(shù)表

3 模擬結(jié)果分析

水平井“分段多簇”壓裂過(guò)程中，由于采用多簇射孔，每個(gè)壓裂段可能形成多條壓裂裂縫，施工參數(shù)、儲(chǔ)層參數(shù)和射孔簇間距等都會(huì)對(duì)多裂縫的形成產(chǎn)生影響，如果部分可控參數(shù)設(shè)置不合理，可能導(dǎo)致部分射孔簇不能開(kāi)啟或不能形成有效的壓裂裂縫，從而降低改造體積，減少壓裂施工的效率。

利用上述計(jì)算模型，主要研究了射孔簇?cái)?shù)、射孔簇間距、儲(chǔ)層參數(shù)、施工參數(shù)等對(duì)水平井“多段分簇”壓裂裂縫干擾規(guī)律的影響。

3.1 射孔簇?cái)?shù)及簇間距

射孔簇?cái)?shù)和簇間距的確定是水平井“多段分簇”壓裂設(shè)計(jì)的核心部分。壓裂段長(zhǎng)度相同，射孔簇?cái)?shù)對(duì)壓裂裂縫有重要影響，射孔簇?cái)?shù)越多，中間的射孔簇越難形成有效壓裂裂縫。

筆者模擬了2簇、3簇和4簇射孔在不同的射孔簇間距條件下的裂縫擴(kuò)展，圖2所示為3簇射孔、不同的射孔簇間距條件下的擴(kuò)展結(jié)果，圖2－a為射孔簇間距為20.0m時(shí)的裂縫擴(kuò)展結(jié)果，中間的射孔簇只能開(kāi)啟小段距離后就發(fā)生止裂，不能形成有效裂縫；圖2－b所示的為射孔簇間距為26.0m時(shí)的裂縫寬度圖，中間的射孔簇產(chǎn)生的壓裂裂縫能擴(kuò)展一段距離，但是裂縫的長(zhǎng)度有限，不到兩端射孔壓裂裂縫的一半；圖2－c所示的是射孔簇間距為30.0m時(shí)的裂縫擴(kuò)展結(jié)果，中間的裂縫長(zhǎng)度只比兩端的裂縫略短，形成了有效裂縫。

假設(shè)中間射孔簇形成的壓裂裂縫長(zhǎng)度達(dá)到兩端裂縫的一半以上，認(rèn)為中間裂縫形成了有效裂縫。不同射孔簇?cái)?shù)、簇間距條件下的裂縫擴(kuò)展情況如圖3所示，從圖3可以看出：射孔簇?cái)?shù)增加，能形成有效裂縫的極限間距增加，且增加幅度較大；射孔簇?cái)?shù)為2簇，極限干擾距離為13.0m；射孔簇?cái)?shù)增加到4簇，極限干擾距離增加到38.0m。

圖2 3簇射孔不同射孔簇間距條件下的裂縫擴(kuò)展模擬結(jié)果圖

圖3 不同射孔簇?cái)?shù)和間距條件下裂縫擴(kuò)展結(jié)果圖

壓裂段的射孔簇?cái)?shù)不同，每簇射孔能形成有效裂縫的最小間距與射孔簇?cái)?shù)密切相關(guān)。射孔簇?cái)?shù)越多，中間裂縫能形成有效裂縫的最小射孔簇間距越大，壓裂裂縫間的干擾越大，中間的射孔簇越難形成有效裂縫。

3.2 儲(chǔ)層參數(shù)

儲(chǔ)層的彈性模量增大，壓裂裂縫寬度降低，這樣會(huì)降低射孔簇間的干擾，增加中間射孔簇壓裂裂縫的長(zhǎng)度。圖4所示的是3簇射孔、彈性模量為5.5×1010Pa時(shí)的裂縫擴(kuò)展情況，圖2－b所示的是3簇射孔、彈性模量為3.5×1010Pa時(shí)的裂縫擴(kuò)展情況，可以發(fā)現(xiàn)：儲(chǔ)層彈性模量增大2.0×1010Pa時(shí)，中間射孔簇的裂縫長(zhǎng)度增加了53.0m，中間裂縫形成了有效裂縫。

圖4 彈性模量為5.5×1010 Pa時(shí)，3簇射孔壓裂的擴(kuò)展結(jié)果圖

彈性模量增大，所有的壓裂裂縫的寬度有一定的降低，但是裂縫寬度降低有助于減少裂縫間的干擾，能增加中間射孔簇裂縫的裂縫長(zhǎng)度。

儲(chǔ)層的抗張強(qiáng)度增加，中間裂縫由于會(huì)受到兩端裂縫的擠壓和干擾，會(huì)導(dǎo)致中間裂縫的開(kāi)啟難度增大，這樣會(huì)加劇射孔簇間的干擾，導(dǎo)致射孔簇間的極限干擾距離增大。

3.3 施工參數(shù)

施工排量較大時(shí)，壓裂裂縫初期的裂縫寬度增加速度較快，會(huì)加劇裂縫間的干擾，特別是射孔簇?cái)?shù)為4簇時(shí)，施工排量的影響尤為明顯。

圖5所示的是4簇射孔、射孔簇間距為38.0m，施工排量分別為12.0m3／min和16.0m3／min時(shí)的裂縫擴(kuò)展情況，施工排量增大4.0m3／min，中間裂縫的長(zhǎng)度發(fā)生了明顯變化；施工排量為16.0m3／min、4簇射孔條件下，中間射孔簇?zé)o法形成有效裂縫。

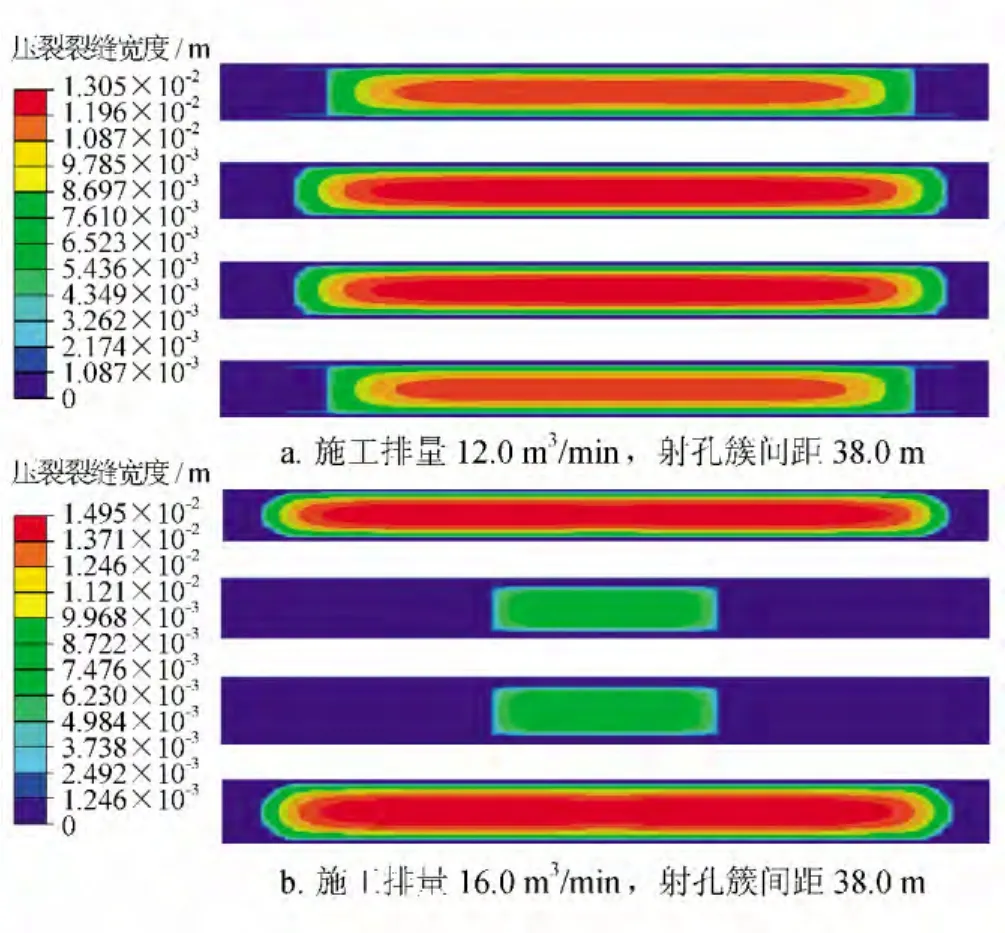
圖5 4簇射孔，不同施工排量下的裂縫擴(kuò)展結(jié)果圖

施工排量增大，壓裂的初始階段各射孔簇形成的裂縫的寬度比低排量形成的裂縫的寬度大，這樣會(huì)加劇裂縫間的干擾，導(dǎo)致中間射孔簇?zé)o法形成有效裂縫。

壓裂液黏度增加，壓裂裂縫的寬度和長(zhǎng)度發(fā)生變化，但是變化不明顯，對(duì)水平井“多段分簇”射孔壓裂的干擾的影響較小。

4 現(xiàn)場(chǎng)應(yīng)用

利用所建立的力學(xué)模型，對(duì)西南某區(qū)塊的一口水平井的每個(gè)壓裂段長(zhǎng)度和射孔簇間距進(jìn)行了優(yōu)化。優(yōu)化的水平井的儲(chǔ)層深度參數(shù)如表2所示，水平井在儲(chǔ)層1的中下部，離該儲(chǔ)層的頂部10.0m，水平井井段長(zhǎng)度為1 000.0m。

表2 優(yōu)化井儲(chǔ)層的深度數(shù)據(jù)表

該水平井的鄰井已進(jìn)行過(guò)壓裂施工，水平段長(zhǎng)為1 000.0m，與將要優(yōu)化的水平井的水平段長(zhǎng)度相同，壓裂總計(jì)15段，每段長(zhǎng)度為66.0m，每個(gè)壓裂段射3簇孔，射孔簇間距為22.0m，壓裂施工后，產(chǎn)量遠(yuǎn)沒(méi)有達(dá)到設(shè)計(jì)的預(yù)期值，通過(guò)對(duì)每簇射孔的流量監(jiān)測(cè)發(fā)現(xiàn)：大部分壓裂段中間的射孔簇幾乎沒(méi)有產(chǎn)量或者產(chǎn)量較小，每個(gè)壓裂段兩端的射孔的產(chǎn)量占總產(chǎn)量的80%以上。產(chǎn)量監(jiān)測(cè)結(jié)果證明中間射孔簇沒(méi)有形成有效的壓裂裂縫。

根據(jù)改造儲(chǔ)層的物性參數(shù)以及相鄰水平井的壓裂施工參數(shù)，對(duì)要優(yōu)化的水平井進(jìn)行了“分段多簇”壓裂裂縫擴(kuò)展模擬，不同射孔簇間距條件下得到的壓裂裂縫長(zhǎng)度如圖6所示（考慮對(duì)稱性，兩端射孔簇的裂縫在圖中只畫(huà)一條曲線）：當(dāng)射孔間距為22.0m時(shí)，中間射孔簇的壓裂裂縫基本沒(méi)有壓開(kāi)，只形成了很短的壓裂裂縫。當(dāng)射孔簇間距為30.0m時(shí)，中間的射孔簇形成的壓裂裂縫和兩端射孔簇形成的壓裂裂縫基本相當(dāng)。因此，壓裂設(shè)計(jì)過(guò)程中，射孔簇的間距設(shè)定在30.0m左右比較合適，根據(jù)射孔簇間距參數(shù)，每個(gè)壓裂段的長(zhǎng)度確定為90.0m，壓裂段數(shù)為11段。

壓裂施工后，通過(guò)對(duì)每段射孔簇的產(chǎn)量進(jìn)行監(jiān)測(cè)發(fā)現(xiàn)：每簇中間射孔都有一定的產(chǎn)量，且差別不是很大。壓裂過(guò)程中減少了4個(gè)壓裂段，但是，優(yōu)化后的井的油氣總產(chǎn)量比鄰井的總產(chǎn)量更高。這樣也證明了設(shè)計(jì)的每簇射孔都形成了比較長(zhǎng)的有效裂縫，間接驗(yàn)證了計(jì)算模型的正確性和指導(dǎo)性。

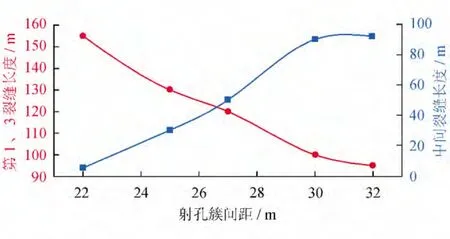
圖6 不同射孔簇間距條件下的裂縫長(zhǎng)度結(jié)果圖

5 結(jié)論

基于流—固耦合的基本方程和損傷力學(xué)的基本原理，建立了水平井“多段分簇”壓裂裂縫擴(kuò)展的三維有限元力學(xué)模型，利用該模型對(duì)水平井“多段分簇”壓裂簇間裂縫干擾進(jìn)行了模擬計(jì)算，通過(guò)模擬發(fā)現(xiàn)：

1）射孔簇?cái)?shù)和射孔簇間距是影響水平井“多段分簇”射孔壓裂簇間裂縫干擾的主要影響因素。射孔簇?cái)?shù)越多，每個(gè)壓裂段裂縫間的干擾越嚴(yán)重，射孔簇間距越小，裂縫間的干擾越嚴(yán)重。

2）施工參數(shù)和儲(chǔ)層參數(shù)會(huì)對(duì)裂縫擴(kuò)展結(jié)果產(chǎn)生一定的影響，其中施工排量對(duì)4簇射孔的影響較大。

3）利用所建立的計(jì)算模型，可以為現(xiàn)場(chǎng)壓裂施工確定射孔簇?cái)?shù)和射孔簇間距提供一定的指導(dǎo)和借鑒。

［1］ 李春芹.水平井分段壓裂在特低滲透油藏開(kāi)發(fā)中的應(yīng)用［J］.西南石油大學(xué)學(xué)報(bào)：自然科學(xué)版，2011，33（6）：85－88.LI Chunqin.Application of horizontal well fracturing technology in thin layer and ultra－low permeability reservoir development［J］.Journal of Southwest Petroleum University：Science ＆ Technology Edition，2011，33（6）：85－88.

［2］ 程遠(yuǎn)方，李友志，時(shí)賢，等.頁(yè)巖氣體積壓裂縫網(wǎng)模型分析及應(yīng)用［J］.天然氣工業(yè)，2013，33（9）：53－59.CHENG Yuanfang，LI Youzhi，SHI Xian，et al.Analysis and application of fracture network models of volume fracturing in shale gas reservoirs［J］.Natural Gas Industry，2013，33（9）：53－59.

［3］ 吳奇，胥云，王騰飛，等.增產(chǎn)改造理念的重大變革——體積改造技術(shù)概論［J］.天然氣工業(yè)，2011，31（4）：7－12.WU Qi，XU Yun，WANG Tengfei，et al.The revolution of reservoir stimulation：An introduction of volume fracturing［J］.Natural Gas Industry，2011，31（4）：7－12.

［4］ 李勇明，彭瑀，王中澤.頁(yè)巖氣壓裂增產(chǎn)機(jī)理與施工技術(shù)分析［J］.西南石油大學(xué)學(xué)報(bào)：自然科學(xué)版，2013，35（2）：90－96.LI Yongming，PENG Yu，WANG Zhongze.Analysis of shale gas fracture stimulation mechanism and operating techniques［J］.Journal of Southwest Petroleum University：Science ＆ Technology Edition，2013，35（2）：90－96.

［5］ 鄒雨時(shí)，張士誠(chéng)，馬新仿.頁(yè)巖氣藏壓裂支撐裂縫的有效性評(píng)價(jià)［J］.天然氣工業(yè)，2012，32（9）：52－55.ZOU Yushi，ZHANG Shicheng，MA Xinfang.Assessment on the effectiveness of propped fractures in the fracturing of shale gas reservoirs［J］.Natural Gas Industry，2012，32（9）：52－55.

［6］ 趙金洲，任嵐，胡永全.頁(yè)巖儲(chǔ)層壓裂縫成網(wǎng)延伸的受控因素分析［J］.西南石油大學(xué)學(xué)報(bào)：自然科學(xué)版，2013，35（1）：1－9.ZHAO Jinzhou，REN Lan，HU Yongquan.Controlling factors of hydraulic fractures extending into network in shale formations［J］.Journal of Southwest Petroleum University：Science ＆ Technology Edition，2013，35（1）：1－9.

［7］ AYERS K L，AMINIAN K，AMERI S.The impact of multistage fracturing on the production performance of the horizontal wells in shale formations［C］∥paper 161347 presented at the SPE Eastern Regional Meeting，3－5October 2012，Lexington，Kentucky，USA.New York：SPE，2012.

［8］ 郭肖，杜志敏.非均質(zhì)性對(duì)水平井產(chǎn)能的影響［J］.石油勘探與開(kāi)發(fā)，2004，31（1）：91－93.GUO Xiao，DU Zhimin.Impacts of permeability heterogeneity on horizontal well productivity［J］.Petroleum Exploration and Development，2004，31（1）：91－93.

［9］ 曾凡輝，郭建春，何頌根，等.致密砂巖氣藏壓裂水平井裂縫參數(shù)的優(yōu)化［J］.天然氣工業(yè)，2012，32（11）：54－58.ZENG Fanhui，GUO Jianchun，HE Songgen，et al.Optimization of fracture parameters of fractured horizontal wells in tight sandstone gas reservoirs［J］.Natural Gas Industry，2012，32（11）：54－58.

［10］ WONG S W，GEILIKMAN M，XU G S.Interaction of multiple hydraulic fractures in horizontal wells［C］∥paper 163982presented at the SPE Middle East Unconventional Gas Conference and Exhibition，28－30January 2013，Muscat，Oman.New York：SPE，2013.

［11］ 趙金洲，王松，李勇明.頁(yè)巖氣藏壓裂改造難點(diǎn)與技術(shù)關(guān)鍵［J］.天然氣工業(yè)，2012，32（4）：46－49.ZHAO Jinzhou，WANG Song，LI Yongming.Difficulties and key techniques in the fracturing treatment of shale gas reservoirs［J］.Natural Gas Industry，2012，32（4）：46－49.

［12］ 胡永全，賈鎖剛，趙金洲，等.縫網(wǎng)壓裂控制條件研究［J］.西南石油大學(xué)學(xué)報(bào)：自然科學(xué)版，2013，35（4）：126－132.HU Yongquan，JIA Suogang，ZHAO Jinzhou，et al.Study on controlling conditions in network hydraulic fracturing［J］.Journal of Southwest Petroleum University：Science ＆ Technology Edition，2013，35（4）：126－132.

［13］ 彪仿俊，劉合，張士誠(chéng)，等.水力壓裂水平裂縫影響參數(shù)的數(shù)值模擬研究［J］.工程力學(xué)，2011，28（10）：228－235.BIAO Fangjun，LIU He，ZHANG Shicheng，et al.A numerical study of parameter influences on horizontal hydraulic fracture［J］.Engineering Mechanics，2011，28（10）：228－235.

［14］ ZIENKIEWICZ O C，TAYLOR R L.The finite element method：An introduction with partial differential equations［M］.Burlington：Elsevier，2005：42－45.

［15］ 董平川，徐小荷.儲(chǔ)層流固耦合的數(shù)學(xué)模型及其有限元方程［J］.石油學(xué)報(bào)，1998，19（1）：64－70.DONG Pingchuan，XU Xiaohe.The fully coupled mathematical model of the fluid－solid in an oil reservoir and its finite element equations［J］.Acta Petrolei Sinica，1998，19（1）：64－70.

［16］ 冉啟全，李士倫.流固耦合油藏?cái)?shù)值模擬中物性參數(shù)動(dòng)態(tài)模型研究［J］.石油勘探與開(kāi)發(fā)，1997，24（3）：61－65.RAN Qiquan，LI Shilun.Study on dynamic models of reservoir parameters in the coupled simulation of multiphase flow and reservoir deformation［J］.Petroleum Exploration and Development，1997，24（3）：61－65.

［17］ ADACHI J，SIEBRITS E，PERICE A.Computer simulation of hydraulic fractures［J］.International Journal of Rock Mechanics ＆ Mining Sciences，2007，44（5）：739－757.

［18］ CAMANHO P P，DAVILA C G.Mixed－mode decohesion finite elements for the simulation of delamination in composite materials［R］.NASA／TM－2002－211737，Hampton，Virginia：Langley Research Center，2002：1－37.

［19］ 李宗利，王亞紅，任青文.自然營(yíng)造力作用下巖石單裂紋水力劈裂數(shù)值仿真模型［J］.巖石力學(xué)與工程學(xué)報(bào)，2007，26（4）：727－733.LI Zongli，WANG Yahong，REN Qingwen.Numerical simulation model of hydraulic fracturing of rock with a single fracture under natural hydraulic power［J］.Chinese Journal of Rock Mechanics and Engineering，2007，26（4）：727－733.

［20］ 張廣明，劉合，張勁.油井水力壓裂流—固耦合非線性有限元數(shù)值模擬［J］.石油學(xué)報(bào)，2009，30（1）：113－116.ZHANG Guangming，LIU He，ZHANG Jin.Simulation of hydraulic fracturing of oil well based on fluid－solid coupling equation and non－linear finite element［J］.Acta Petrolei Sinica，2009，30（1）：113－116.