靜電陀螺監控器低緯度避免標定重置的快速預測方法

（1. 中國衛星海上測控部，江陰 214431；2. 天津航海儀器研究所，天津 300131）

（1. 中國衛星海上測控部，江陰 214431；2. 天津航海儀器研究所，天津 300131）

在低緯度地區，靜電陀螺監控器48 h標定階段易出現上陀螺高度角低于限定值，導致標定重置的問題。為了避免標定重置問題的出現，根據轉子自轉軸空間指向的變化特點，利用上陀螺的測角數據、慣導航向和位置數據，綜合船舶運動、地球自轉、殼體旋轉的影響，推導出了預測上陀螺高度角的計算方法，并提出了適時調整載體所處緯度的規避方案。根據計算結果繪制了轉子自轉軸空間運動軌跡，實現了標定重置時間點的預測，預測誤差小于3 min。該方法只需要很少的原始測量數據，預測精度高，提出的規避方案可操作性強，具有一定的推廣應用價值。

靜電陀螺儀；高度角；方位角；標定

靜電陀螺監控器是當前導航精度最高的慣性設備，平臺式靜電陀螺監控器在低緯度地區（5°S～5°N）啟動運行時，48 h標定階段易出現標定重置的問題，導致系統無法轉入導航狀態[1-2]。

受標定方案的約束，當靜電陀螺監控器上陀螺的高度角小于hp時，濾波器和標定時間均會重置[3]。通過對數據分析，發現標定重置時上陀螺的高度角剛好滿足約束條件。

平臺式靜電陀螺儀轉子在軸向質量不平衡擺性力矩的影響下，其空間指向并非恒定的，主要漂移誤差源是轉子非球形的奇次諧波，即為一次靜電力力矩產生的g1項漂移。g1項漂移主要表現形式為轉子自轉軸在慣性空間做勻速錐擺運動，每一個陀螺儀對應的錐角以及運動的角速度各異[4]。當靜電陀螺監控器處于低緯度地區時，由于g1項漂移的影響，隨著時間的推移很容易使上陀螺高度角滿足標定重置條件。

調整載體所處緯度是改變上陀螺高度角的直接而有效的方法，但是調整時機和緯度調整范圍必須要充分考慮陀螺儀的實際漂移特性[5]。

本文對上陀螺轉子自轉軸空間指向的計算公式進行了推導，給出了利用靜電陀螺監控器有限時段的測量數據計算g1項漂移對應錐角和角速度的方法，并結合地球自轉角速度，完成了系統標定重置時間點的快速預測和載體最小緯度調整范圍的確定。

1 陀螺儀支撐框架坐標系與慣性坐標系

1.1 陀螺儀支撐框架坐標系

1.1.1 陀螺儀支撐框架坐標系

靜電陀螺儀安裝于由方位環和高度環所確定的支撐框架內，靜電陀螺監控器系統所能提供的陀螺儀測量數據主要有高度角和方位角，為確定靜電陀螺儀轉子自轉軸在慣性空間的指向，首先應當確定其在陀螺儀支撐框架內的坐標。在陀螺儀高度角和方位角均為0°時，高度環兩軸端的連線與方位環兩軸端的連線的交點即為陀螺儀支撐框架坐標系的原點oc；高度環兩軸端連線為xc軸，指向船右弦；方位環兩軸端連線為zc軸，指向上；由右手法則可知yc軸，指向船艏向。

1.1.2 上陀螺高度角和方位角

上陀螺高度角和方位角的定義如圖1所示。在陀螺儀支撐框架坐標系中，從右弦側向左看，高度環逆時針旋轉一周，上陀螺高度角由0°遞增至360°；從上向下俯視，方位環逆時針旋轉一周，上陀螺方位角由0°遞增至360°。

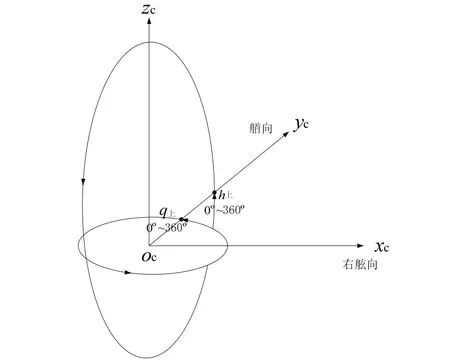
圖1 上陀螺高度角和方位角Fig.1 h angle and q angle of polar axis gyroscope

1.1.3 陀螺儀支撐框架坐標系中的三維坐標

根據靜電陀螺監控器所測量的陀螺儀高度角和方位角可知，陀螺儀殼體幾何中心軸在陀螺儀支撐框架坐標系的指向，假設該中心軸上的一點a到坐標原點的距離為1，則該點在上陀螺支撐框架坐標系中的三維坐標如式(1)所示：

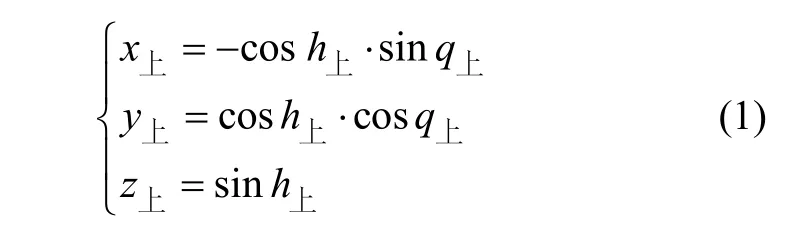
1.2 慣性坐標系

1.2.1 慣性坐標系

為便于后續計算，某一時刻慣性坐標系定義如圖2所示。

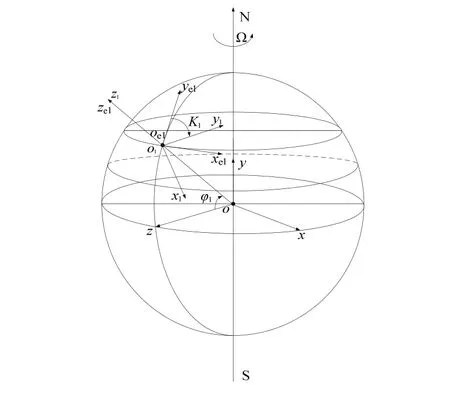
圖2 慣性坐標系的定義Fig.2 The definition of inertial coordinate system

圖2中，地心為慣性坐標系的原點o，y軸與地球自轉軸重合，x軸與z軸均在赤道面上，其中z軸指向靜電陀螺監控器慣性平臺所處位置對應經度線與地球赤道的交點，x軸的指向遵循右手法則。

1.2.2 陀螺儀支撐框架坐標系與慣性坐標系的關系

靜電陀螺監控器通過無減速隨動系統控制平臺的橫搖環和縱搖環跟蹤慣導水平，為靜電陀螺儀提供了良好的工作環境，保證了圖1中陀螺儀支撐框架坐標系x1o1y1平面與當地地理水平面平行。

在圖2中，o1-x1y1z1為陀螺儀支撐框架坐標系，假設在t1時刻船舶航向為K1，所處經度為λ1，緯度為φ1，在忽略復示平臺復示水平誤差和慣導航向測量誤差的情況下，陀螺儀支撐框架坐標系通過兩次坐標旋轉即可得到慣性坐標系：

① o1-x1y1z1繞z1軸逆時針旋轉K1，可以得到當地地理水平坐標系oe1-xe1ye1ze1；

② oe1-xe1ye1ze1繞xe1軸逆時針旋轉φ1，即可得到慣性坐標系o-xyz。

假設在t1時刻，1.1.3中a點在陀螺儀支撐框架坐標系中的三維坐標為(x1, y1, z1)，則a點在慣性坐標系的坐標為：

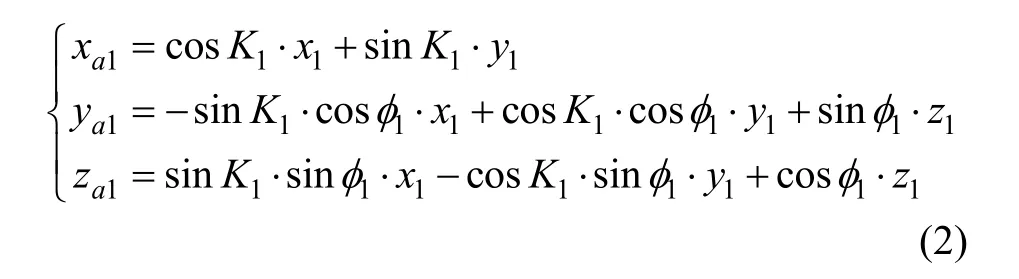
2 陀螺儀轉子自轉軸空間指向

2.1 船舶運動和地球自轉對陀螺儀的影響

在t2時刻，船舶航向為K2，所處經度為λ2，緯度為φ2，相對于t1時刻經度變化量為：

該時段內地球在慣性空間內轉動的角度為：

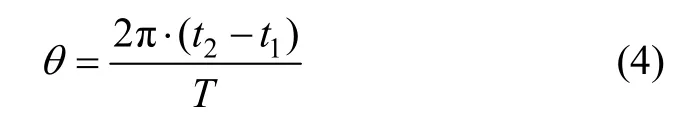
式中，T為地球在慣性空間內自轉一周的時間，為23∶56∶4。則t2時刻陀螺儀支撐框架坐標系o2-x2y2z2需要經過三次坐標旋轉方可得到1.2節定義的慣性坐標系：

① o2-x2y2z2繞z2軸逆時針旋轉K2，得到地理水平坐標系oe2-xe2ye2ze2；

② oe2-xe2ye2ze2繞xe2軸逆時針旋轉φ2，得到坐標系oe3-xe3ye3ze3；

③ oe3-xe3ye3ze3繞ye3軸順時針旋轉δλ+ θ即可得到慣性坐標系o-xyz。

假設在t2時刻，1.1.3中a點在陀螺儀支撐框架坐標系中的三維坐標為(x2, y2, z2)，則a點在慣性坐標系的坐標為：

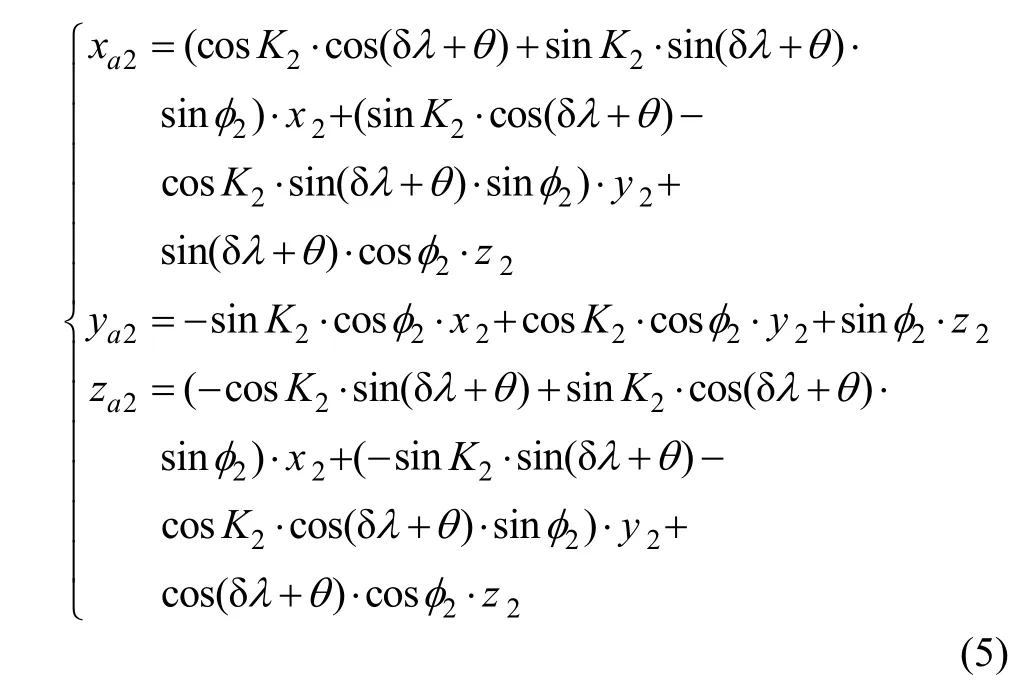
2.2 殼體旋轉對陀螺儀的影響

靜電陀螺儀在工作的過程中，殼體繞其幾何中心軸旋轉，約4 min轉一周。靜電陀螺儀殼體自轉的過程中，設備通過減速器隨動系統控制高度環和方位環轉動，以保證殼體光電傳感器中心點m始終對準轉子的自轉軸。該點與陀螺儀支撐框架坐標系原點的連線和陀螺儀自轉軸重合。若以該點為參考點，則陀螺儀幾何中心軸繞轉子轉動的角度與殼體旋轉角度大小相等。如圖3所示，om與a1ma2平面相垂直，若a1、a2對應的殼體旋轉角分別為ρ1、ρ2，則：

2.3 陀螺儀轉子自轉軸的實際空間指向

圖 3中在|oa1|、|oa2|均為1的情況下，且 a1、a2在慣性坐標系 o-xyz中的坐標分別為(xa1, ya1, za1)和 (xa2, ya2, za2)，則：

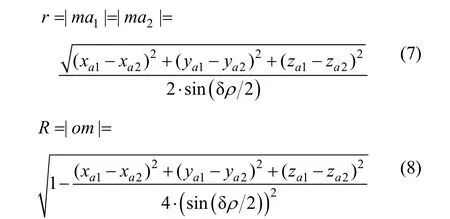
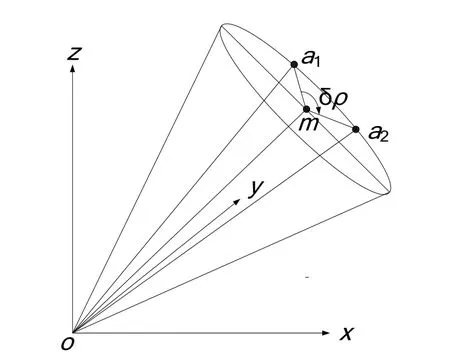
圖3 殼體旋轉相對關系Fig.3 The relationship of shell rotations

設m點在慣性坐標系o-xyz中的坐標為(xm, ym, zm)，可以建立如下以xm、ym、zm為未知數的三元方程組[6]：

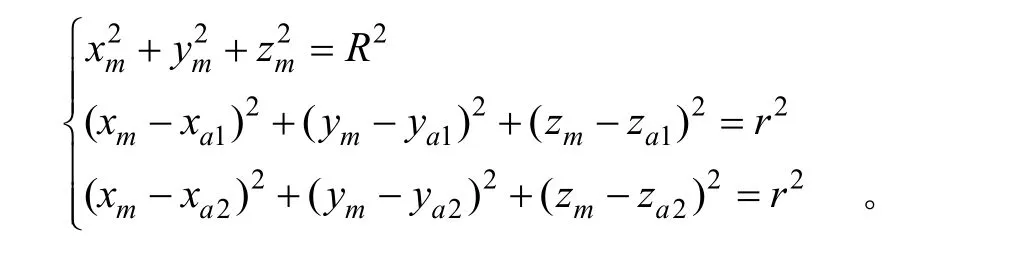
通過Matlab等計算工具可以方便地求得方程組的解，由于方程組解的表達式過長，文中沒有列出。利用方程組解的表達式，對某型靜電陀螺監控器25.5 h的數據進行了處理，完成了上陀螺m點在慣性空間坐標計算，繪制了 m點在慣性坐標系下的運動軌跡以及轉子自轉軸與赤道面的夾角變化情況，分別如圖4、圖5所示。

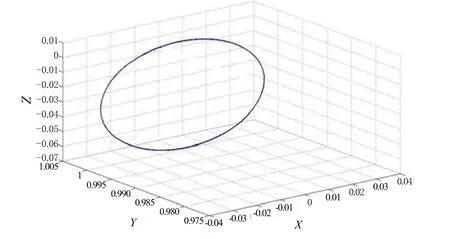
圖4 上陀螺m點在慣性坐標系下的運動軌跡Fig.4 Trajectory of point m of up gyro in inertial coordinates

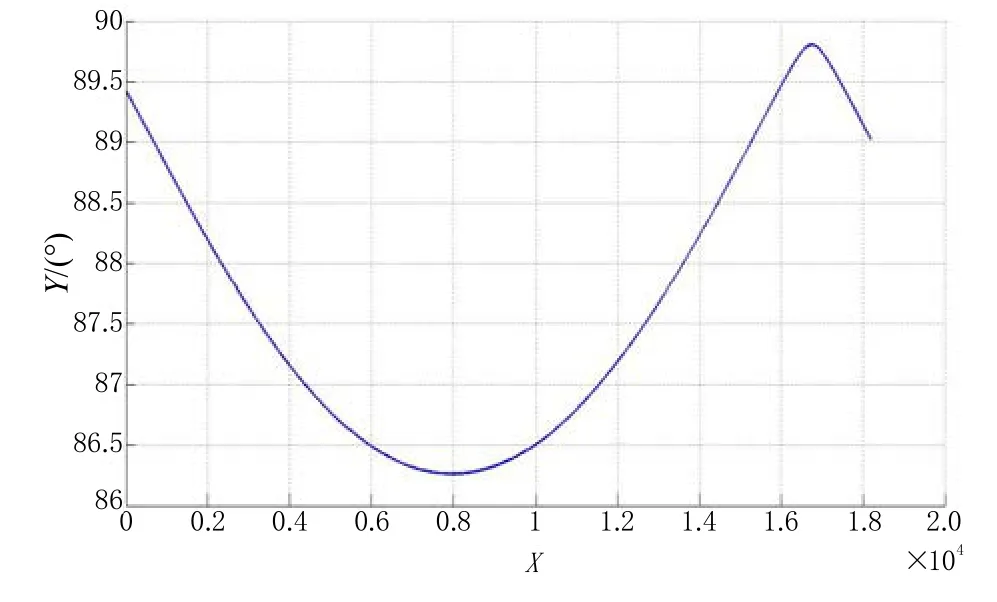
圖5 上陀螺轉子自轉軸與赤道面夾角變化情況Fig.5 Rotor shaft of up gyro vs. equatorial plane angle

3 陀螺儀高度角的計算與預測

3.1 錐角和錐擺角速度

如圖4所示，m點在空間中做圓周運動，假設圓心坐標為(xo, yo, zo)，根據2.3節計算出m點運動過程中四點的三維坐標，利用圓周上的點到圓心距離相等的關系，建立三元二次方程組，便可求解出圓心的坐標，則錐角為：

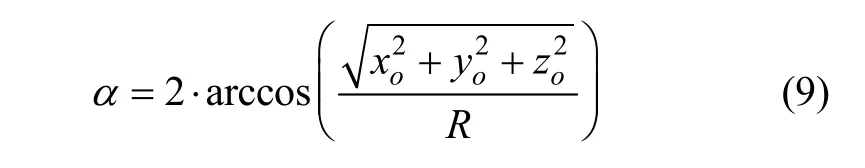
根據2.3節計算出m點在任意兩時刻的坐標分別為(x1, y1, z1)、(x2, y2, z2)，時間間隔為t，則錐擺的角速度為：

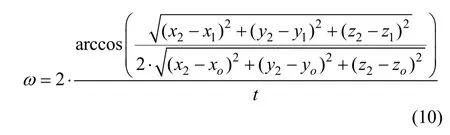
據此可以計算出任意時刻m點的坐標(xm, ym, zm)。

3.2 陀螺儀高度角的計算與預測

根據2.3可知，陀螺儀殼體幾何中心軸與轉子自轉軸的夾角應為：

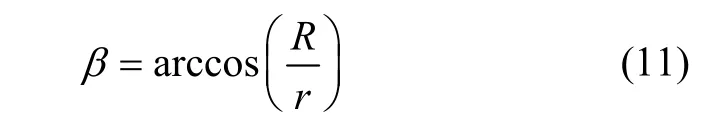
參考2.1節，對慣性坐標系按照下列順序進行旋轉即可由慣性坐標系得到陀螺儀支撐框架坐標系：

① o-xyz繞y軸逆時針旋轉δλ+ θ，得到坐標系oe3-xe3ye3ze3；

② oe3-xe3ye3ze3繞xe3軸順時針旋轉φ2，得到地理水平坐標系oe2-xe2ye2ze2；

③ oe2-xe2ye2ze2繞ze2軸順時針旋轉K2，可以得到陀螺儀支撐框架坐標系o2-x2y2z2。

m點在陀螺儀支撐框架坐標系下的坐標為：

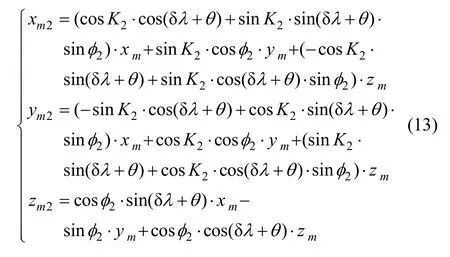
陀螺儀殼體旋轉周期約為4 min，陀螺漂移對應的錐擺運動屬于緩動，故4 min時間內上陀螺高度角h上的變化范圍為：

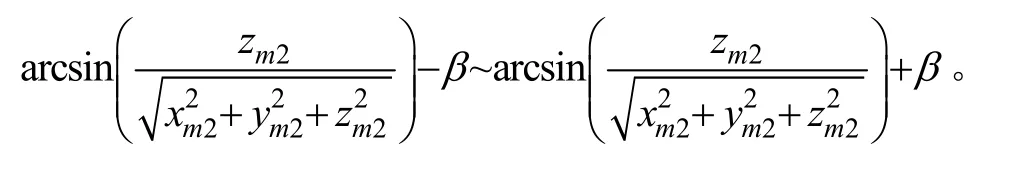
4 陀螺儀高度角預測結果驗證

某型靜電陀螺監控器工作于低緯度地區出現過多次標定重置的情況，根據推導出的預測計算方法，利用設備記錄的陀螺儀隨動后 10 min的數據對標定重置時間進行了預測。預測時間點和實際重置時間點的比較見表1。

表1 標定重置預測情況統計Tab.1 Prediction statistics of calibration reset

從表1統計情況看，標定重置時間點的預測誤差小于3 min。h上≤hp時系統標定將重置，由于地球自轉和陀螺儀的錐擺運動具有規律性，屬不可控因素。若載體在地球上靜止不動，陀螺儀隨動后任意時刻，上陀螺的高度角按照文中推導的方法進行計算是準確的，系統標定重置的時間點可據此進行準確預測，這與統計結果相符。根據陀螺儀的運動特性，通過調整載體的位置，特別是所處的緯度，可以使得系統在標定的過程中上陀螺高度角始終大于hp，在實際應用中，有效保證了系統標定的順利進行。

5 結束語

根據靜電陀螺儀自轉軸在慣性空間的漂移特性，結合工程應用中靜電陀螺監控器內部高度角和方位角定義方式和殼體旋轉的特點，深入分析了靜電陀螺儀高度角、方位角與陀螺儀轉子自轉軸之間的對應關系，利用轉子自轉軸的錐擺特性，推導出任意時刻點靜電陀螺儀高度角的計算方法。提出了調整載體所處緯度規避靜電陀螺監控器標定重置的方案，該方案具有一定的推廣應用價值。

（References）：

[1] 吳旭賢，周海淵，程龍，等. 航天測量船靜電陀螺監控器海上動態標定[J]. 中國慣性技術學報，2012，20(4)：399-404.

WU Xu-xian, ZHOU Hai-yuan, CHENG Long, et al. Dynamic calibration of ESGM on TT&C ship at sea area [J]. Journal of Chinese Inertial Technology, 2012, 20(4): 399-404.

[2] 孫昊，吳旭賢，李長波. 航天測量船靜電陀螺監控器標定分析與應用[J]. 中國慣性技術學報，2013，21(2):: 159-163.

SUN Hao, WU Xu-xian, LI Chang-bo. ESGM calibration analysis and application on TT&C ship[J]. 2013, 21(2): 159-163.

[3] 劉新明，孫學成，周琳琦，等. 靜電陀螺監控器海上“六次校”方法[J]. 中國慣性技術學報，2011，19(4)：399-402.

LIU Xin-ming, SUN Xue-cheng, ZHOU Lin-qi, et al. Method of electrostatic gyroscope monitor’s maritime sixtimes calibration[J]. Journal of Chinese Inertial Technology, 2011, 19(4): 399-402.

[4] Sun Feng, Sun Wei, Gao Wei, et al. Research on the technology of rotation motion for FOG strapdown inertial navigation system[C]//Processing of the 2009 IEEE International Conference on Mechatronics and Automation. Changchun, China, 2009: 4913-4918.

[5] Landau B E, Yemelyantsev G I, Odinstsov B V. Electrostatic gyroscopes in attitude reference systems for orbital spacecrafts: The results of flight tests[C]//Proceedings of 2010 International Symposium on Inertial Technology and Navigation. Nanjing, China, 2010: 18-28.

[6] Zhang Kezhi, Tian Weifeng, Qian Feng. Combination of distributed Kalman filter and BP neural network for ESG bias model identification[J]. Transactions of Nanjing University of Aeronautics & Astronautics, 2010, 27(3): 226-231.

靜電陀螺監控器低緯度避免標定重置的快速預測方法

王前學1，倪文秀2，劉新明1，周海淵1

Rapid prediction method for avoiding ESGM’s calibration reset in low latitude area

WANG Qian-xue1, NI Wen-xiu2, LIU Xin-ming1, ZHOU Hai-yuan1
(1. China Satellite Maritime Tracking & Controlling Department, Jiangyin 214431, China; 2. Tianjin Navigation Instrument Research Institute, Tianjin 300131, China)

During ESGM’s 48 h calibration phase at low latitudes, it may occur that the altitude angle of pole gyro is below the threshold, resulting in the problem of calibration reset. In order to solve this problem, a calculation method for predicting the altitude angle was derived based on the directive characteristics of rotor shaft by using various navigation data and taking account of various influences. In addition, an avoidance scheme for timely adjusting the vehicle at a latitude was put forward. The method requires only a few original measurement data and possesses such advantages as high forecast precision and high maneuverability, showing that it is worthy of broad application.

electrostatic suspended gyroscope; h angle; q angel; calibration

1005-6734(2014)06-0707-04

10.13695/j.cnki.12-1222/o3.2014.06.002

U666.1

A

2014-07-27；

2014-10-23

王前學（1984—），男，工程師，從事慣性導航設備應用研究。E-mail：qianxuewang@163.com