邊緣CPF算法及在重力梯度輔助導航中應用

（1. 哈爾濱工程大學 理學院，哈爾濱 150001；2. 哈爾濱工程大學 自動化學院，哈爾濱 150001）

（1. 哈爾濱工程大學 理學院，哈爾濱 150001；2. 哈爾濱工程大學 自動化學院，哈爾濱 150001）

慣導固有原因使得載體長時間航行累積大量誤差。可通過重力梯度量測與慣導組合導航方法來修正導航誤差。先對重力梯度儀與慣導組合導航原理進行闡述，提出重力梯度儀輔助 INS (GAINS)的系統框架圖，對導航用重力梯度圖和重力梯度儀進行分析，設定組合量測方程。然后根據狀態空間方程的特點，提出使用邊緣Cubature粒子濾波(CPF)進行融合估值。通過理論方法證明其對方差的減小，同時給出算法流程。相同條件下與已有APO-PF算法仿真進行經緯度RMSE結果對比，表明該算法估值精度更高；并用CEP對導航誤差研究，得到在性能較低的慣導條件下、在梯度儀1E2和10 E2噪聲下4h的CEP數值分別為0.044 n mile和0.072 n mile的結果。最后對狀態方程簡化，定性分析出其余狀態量的估值效果。

重力梯度儀輔助慣性導航系統；邊緣濾波；狀態分解；Cubature粒子濾波；圓誤差概率

精確可靠的導航系統是運載器航行關鍵技術。潛艇長時間水下航行會累積導航誤差，而常用的矯正手段GPS信號在水下無法接收，所以需要增加其它的輔助手段。現在有重力/慣性、地形/慣性組合均為研究熱點。但理想導航系統工作將是無源的、自動的，不需要發射和接收信號，其中，重力儀和重力梯度儀量測完全是無源的，不易受到外界干擾源干擾，且重力場空間分布特征比較穩定。因此重力和重力梯度輔助導航是水下無源輔助導航的重要方法。

重力輔助導航目前廣泛采用的是基于最近等值線點匹配的(ICCP)方法，然而這種方法是在航行一段時間后對狀態調整的方法，并且在較大初始誤差下就發散[1]，即便不發散也常會收斂到局部極小。重力的濾波方法由于重力圖在重力變化平緩區域的相似性，經常造成誤匹配而誤差較大。與重力異常相比，重力梯度能反映重力場(重力加速度矢量)全空間變化率，有5個相互獨立的張量。從技術發展角度看，重力量測很難再獲得更高分辨率的重力場特征，重力梯度測量則可進一步提高重力場測量的精度和空間分辨率，量測高精度必然使組合導航精度進一步提高。高精度重力梯度圖的實現目前在海洋測量領域越來越成熟，逼近程度也越來越精細。

已有重力梯度融合研究較少。非線性濾波方法主要有基于EKF的SITAN算法[2]，但該算法在遠離真值的位置進行線性化時經常發散；還有使用UKF直接進行非線性傳遞[3]，但UKF使用Sigma樣本點數量有限，并不能總是包含真正位置點。近期人工物理優化濾波方法被提出，它采用粒子濾波方法，通過調整在重采樣階段粒子間作用力，改變狀態后驗分布，克服粒子退化問題，取得了較穩定效果，位置定位誤差在140 m左右[4]。雖然誤差仍然較大，但說明非線性粒子濾波的可行性。

1 重力梯度輔助導航

重力梯度是重力加速度g的全空間導數，也是重力勢的二階導數[5]，單位為厄特弗斯，用E或EU表示，1 E= 1 mGal/10 km。由于重力梯度具有對稱性和泊松方程的存在，所以實際上有五個獨立的張量Γij(i=x,y,z;j=x,y,z)，分別對應不同方向上重力梯度分量。相比于重力異常，它包含了重力場高階分量，“區別”和“特征”也更明顯。已有重力異常濾波輔助導航定位精度不高，在300～500m之間，就是重力異常包含信息量少的緣故。

忽略垂直通道誤差，GAINS導航原理說明如下：INS加速度計量測載體想要的加速度里含有重力分量，其中法向分量能夠計算補償，但異常分量無法獲取，所以這時的加速度由于加速度計與陀螺儀誤差使誤差隨時間的增長而發散。

重力梯度儀獨立于運載器加速度而量測重力場，不含重力儀的厄特弗斯效應，所以其值可用來糾正慣導加速度計輸出中異常重力分量。重力梯度儀結合 INS的導航性能相比于傳統純慣導情形有較大幅度提高。但由于慣導和重力梯度儀誤差，無圖情況下GAINS的東向位置誤差仍然會有不斷增長的情況。

重力梯度圖獲得條件下，實現慣導與重力梯度圖匹配模式，這種情況下能將實時采集的重力場值和組合系統提供的指示位置在圖上得到的計算值做差比較，通過相應濾波算法給出載體實時位置估計，以來限定位置和速度誤差。所以圖匹配模式是被廣泛研究的組合方式[2-4]。

圖模式間接反饋的系統框架圖如圖1所示。

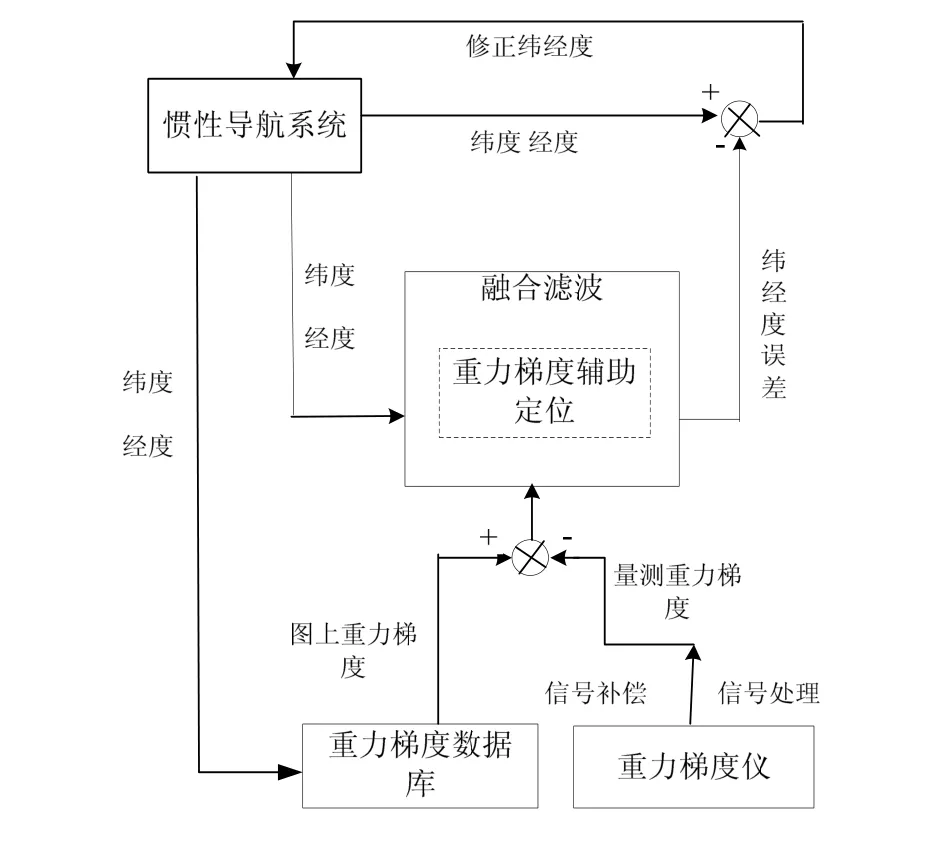
圖1 慣導/重力梯度儀導航結構圖Fig.1 Configuration for INS/gravity gradiometer navigation

可見 GAINS系統三個重要組成部分為重力梯度數據庫、重力梯度儀和數據融合算法。

導航重力梯度庫圖需事先存儲裝配到載體上，一般采用離散網格化的形式存儲，量值與位置坐標一一對應。當前輔助定位基準梯度圖采用實際量測完成的較少，主要是通過理論方法逼近重力梯度。數字高程模型(DEM)正演重力梯度是理論方法逼近重力梯度一種重要形式。DEM主要下載自美國國家地球物理數據中心，它通過假定地面密度常值獲得重力場。另外一種是通過自由空間重力異常轉化。由于自由空間重力異常包含了周圍地形和地下介質共同作用引起的重力梯度，特征更明顯。若自由空間重力異常數據分辨率較低時，單獨構圖反映不了梯度高頻特征，這時可與DEM聯合構圖能取得精細效果[6]。本文所用導航梯度圖示例如圖3所示。

GAINS的重力梯度儀當前主要使用的是貝爾公司的一種旋轉加速度計重力梯度儀。它安裝在慣導組件平臺上一個緩慢旋轉的固定平臺裝置上，每一個重力梯度儀包含4～8個加速度計，加速度計垂直于旋轉軸，其值通過對提取加速度計信號放大處理獲取。為了量測5個獨立重力梯度分量，需要3個重力梯度儀，單重力梯度儀只能量測重力梯度中的兩個分量。

目前國外重力梯度儀有較快的發展和較高的精度。與國外相比，國內部分科研院所從2000年開始對國外重力梯度儀及相關技術跟蹤論證和實驗研究。但由于技術復雜，從目前已有文獻看，國內還不具備制造能實際使用有較高精度重力梯度儀的能力。

融合就是濾波部分。融合算法本文仍然以粒子濾波為基礎，根據重力梯度導航系統狀態方程線性、量測方程是狀態量非線性特點，提出采用邊緣Cubature粒子濾波進行狀態估計。CKF算法與粒子濾波結合在導航上能使粒子群更快向高似然區移動。

2 邊緣Cubature 粒子濾波

2.1 Rao-Blackwell理論

邊緣濾波又稱Rao-Blackwellised濾波，它是根據統計上的Rao-Blackwell理論[7]。該理論說明統計量在某個函數條件下，通過計算條件均值能提高其估值。它的核心是表示統計量條件和非條件方差之間的關系。具體如下：

對兩個變量 U,Y的估計量τ ( U,Y)，非條件方差可以表示為條件方差的和：

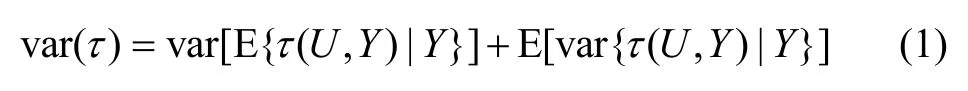
此公式的理論依據是條件均值性質：

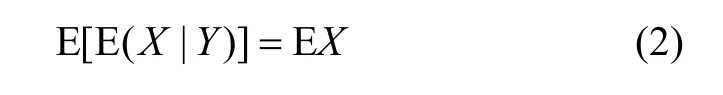
2.2 線性/非線性模型

包括重力梯度導航用一類線性非線性模型為：

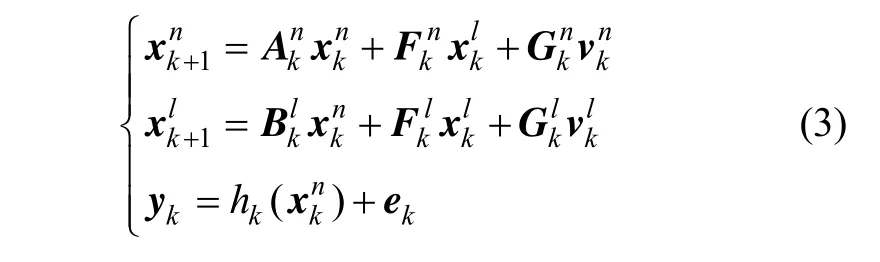
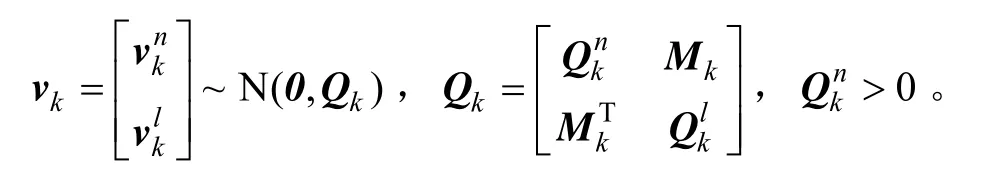
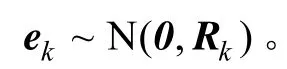
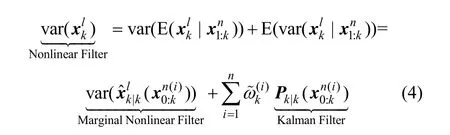
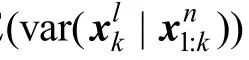
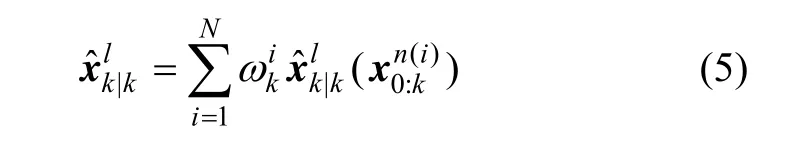
2.3 狀態估計過程推導

粒子濾波雖然可以全空間采樣而且計算快捷，但會出現樣本貧化問題。這里將CKF引入時間更新的重要性采樣函數中。CKF是根據Spherical-Radial Cubature準則，通過一組具有相同權重的點結合最新量測，經非線性系統轉換后產生新的點給出下一時刻系統狀態的預測，其精度可達到三階[9]。該濾波方法與粒子濾波結合使粒子更快向高似然區移動，在導航應用中得到很高的精度。下面對兩種濾波的結合進行推導。

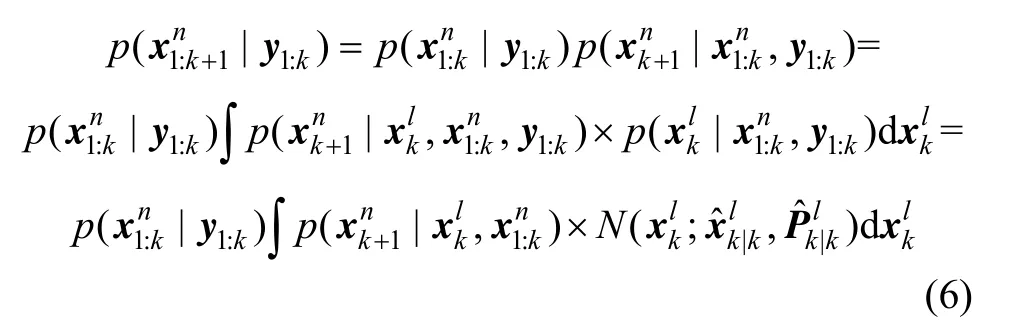
線性狀態估值在時間更新階段為額外的噪聲，時間更新分布是：

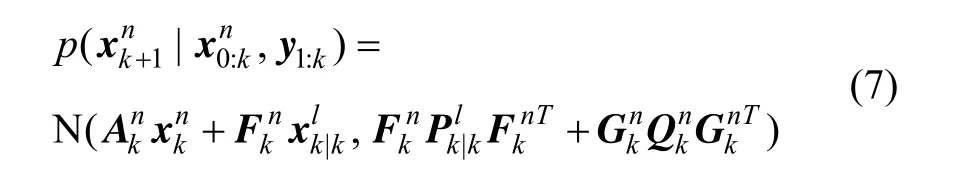
在時間更新階段引入CKF，CKF作用的模型為：

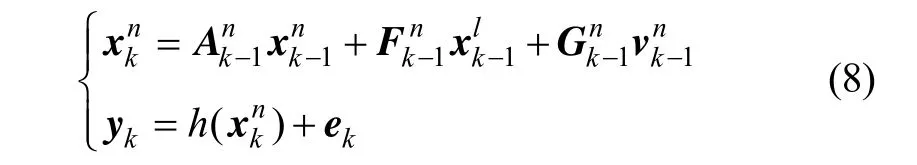
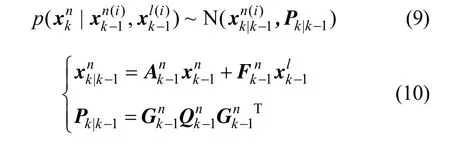
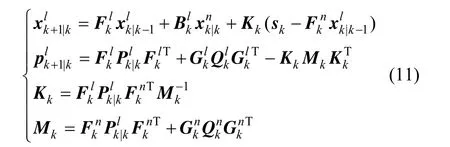
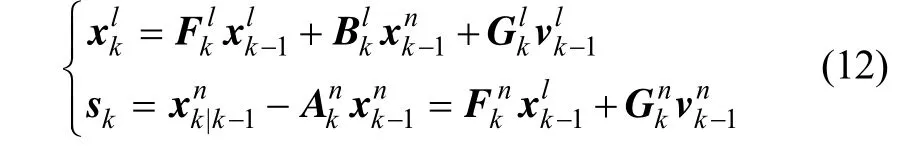
① 計算Cubature點：

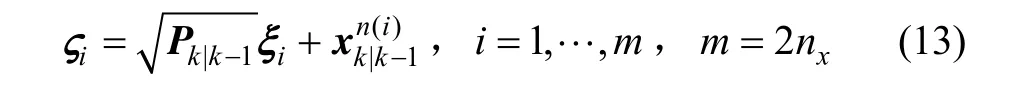
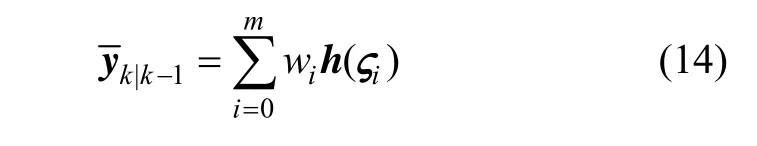
③ 自相關協方差陣：

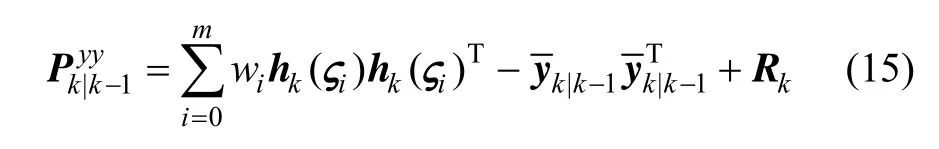
④ 互相關協方差陣：

⑤ 近似卡爾曼增益：

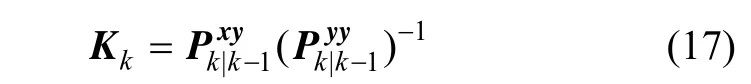
⑥ 后驗均值和協方差：

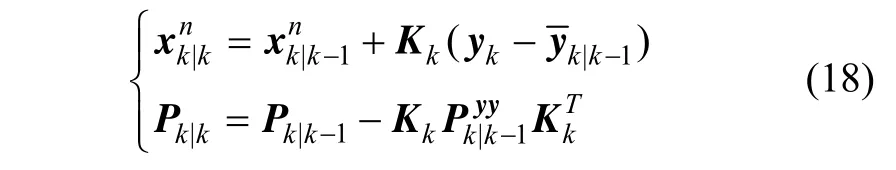
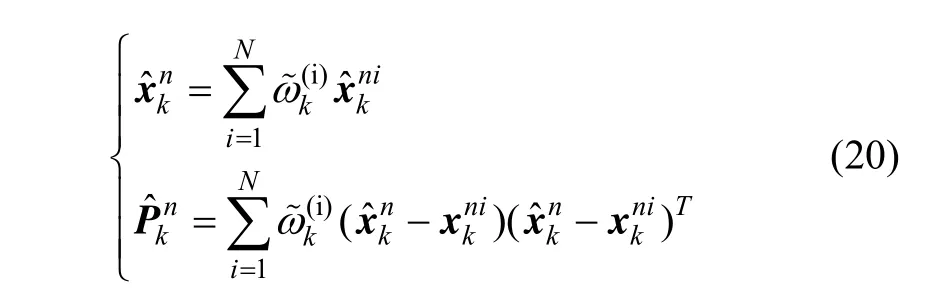
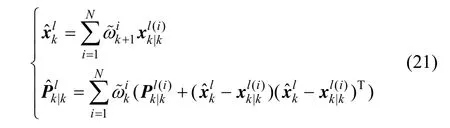
狀態整體后驗分布為：

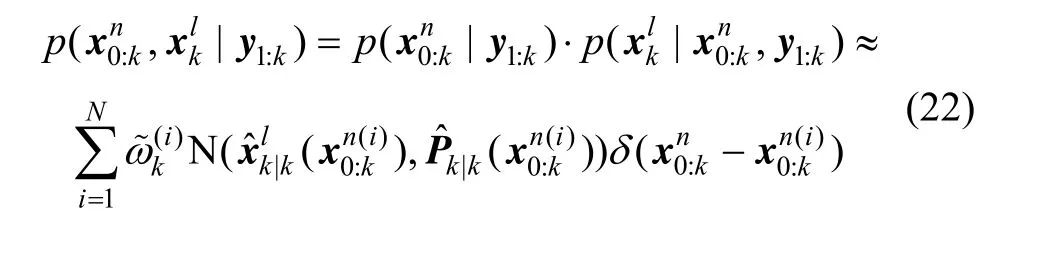
3 邊緣CPF重力梯度輔助導航仿真實例

此處慣性導航系統為平臺慣導，所用數據為船舶航行實際數據，潛艇潛航一般在24 h以上。這里進行仿真驗證，數據時長取7 h，數據采樣周期為1 s，并假設梯度圖制圖精準，不包含圖誤差。導航器件性能較低，如表1所示。載體軌跡、速度如圖2所示。

表1 陀螺和加速度計主要性能參數Tab.1 Parameter of gyro and accelerometer

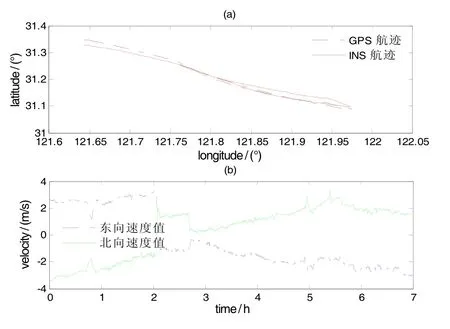
圖2 載體軌跡速度圖Fig2 Vehicle track and velocity

基準梯度圖采用自由空間重力異常正演的重力梯度，分辨率30′。圖3列出北向值沿北向分解的 Γxx和東向值沿北向分解的 Γxy兩幅。

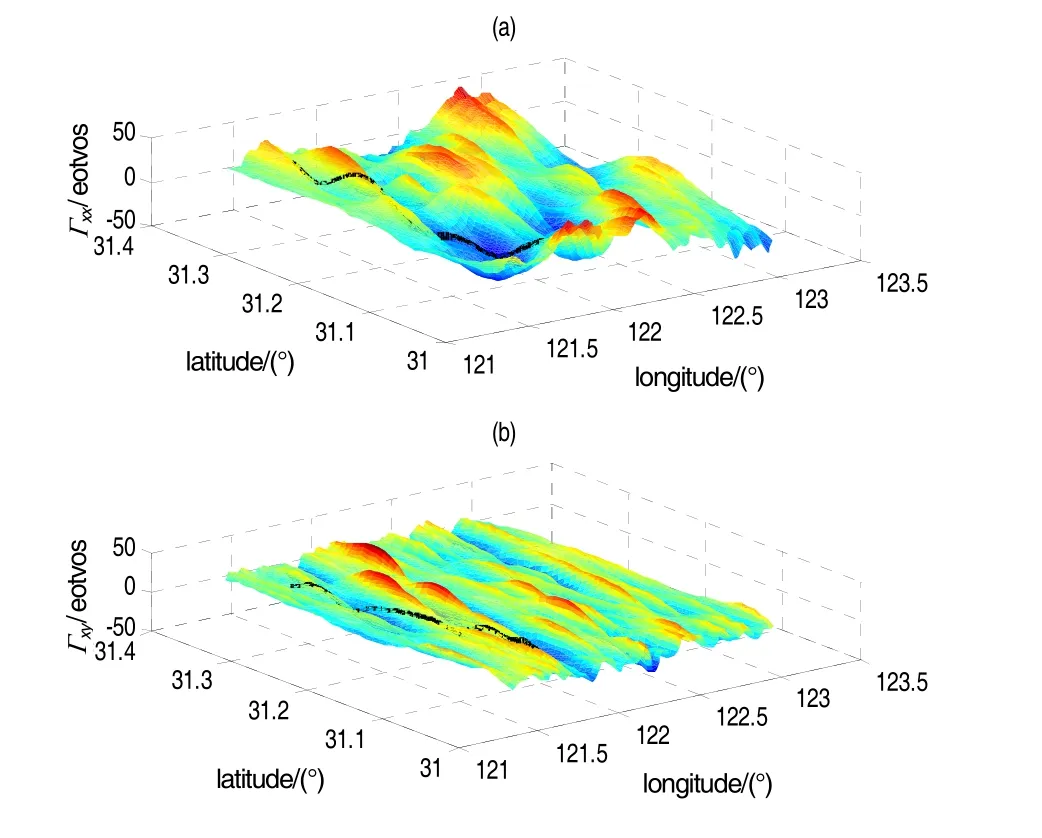
圖3 導航用重力梯度圖 Γ xx和 ΓxyFig.3 Gravity gradient map Γ xxand Γxy

重力梯度儀量測值這里采用真實位置的梯度值加上白噪聲模擬。

3.1 濾波計算

此處采用平臺慣導系統。狀態是間接量緯度經度誤差(δφ, δλ)、東向北向速度誤差(δVx,δVy)、水平方位姿態誤差(α,β,γ)、加速度計零位偏差(Δ Ax,Δ Ay)和陀螺常值漂移(εx,εy,εz)，系統方程為：

式中，X表示12維狀態，狀態矩陣A和噪聲矩陣G表達式參見文獻[4]。系統噪聲W為

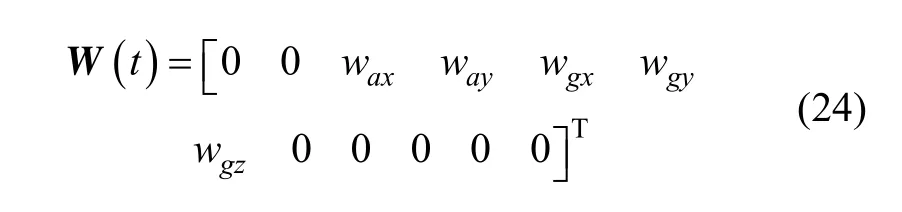
式中， wax、 way、 wgx、 wgy和 wgz均為零均值的高斯白噪聲，分別對應加速度計誤差和陀螺隨機漂移。設濾波周期 Tf=10 s，將狀態方程離散化，離散化后表達式：

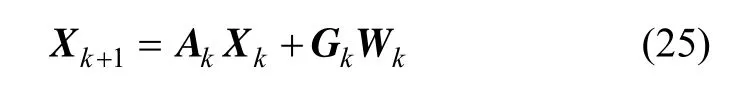
其中，

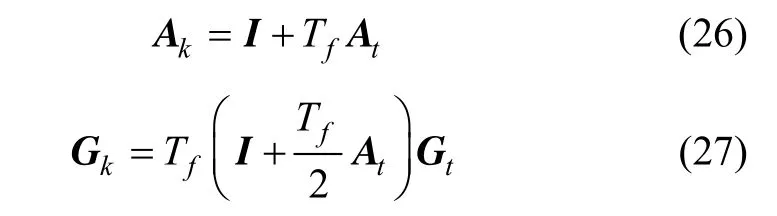
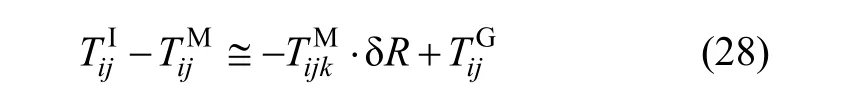
由式(28)知，量測方程是狀態δL和δλ的非線性函數，而且如果位置誤差越小，則梯度之間的差值越小。經緯度誤差用粒子集表示，如果粒子能代表位置的真實后驗分布，則其對應權值就較大，反之較小。粒子濾波通過遞推和更新，可不斷估計慣導的位置誤差，從而校正系統位置輸出。

由于重力梯度數據庫以網格形式給出，對于不在網格上坐標梯度值可通過雙線性插值獲得。海洋中能利用高精度重力梯度儀，噪聲可達1Eotvos或更高精度，仿真中設置分量的量測噪聲為ij= 10E2。

經緯度誤差在量測方程中屬于非線性狀態，余下誤差為線性狀態，將狀態方程 Ak按照式(3)進行分解：

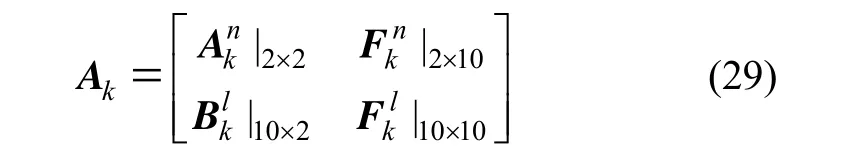
將狀態方程噪聲矩陣分解：

濾波時設引入重力梯度輔助定位時的位置誤差已達2000 m，仿真粒子數 N= 100，進行10次Monte Carlo仿真，相同條件下濾波穩定后位置均方根誤差(RMSE)與APO-PF算法比較結果如圖4所示。

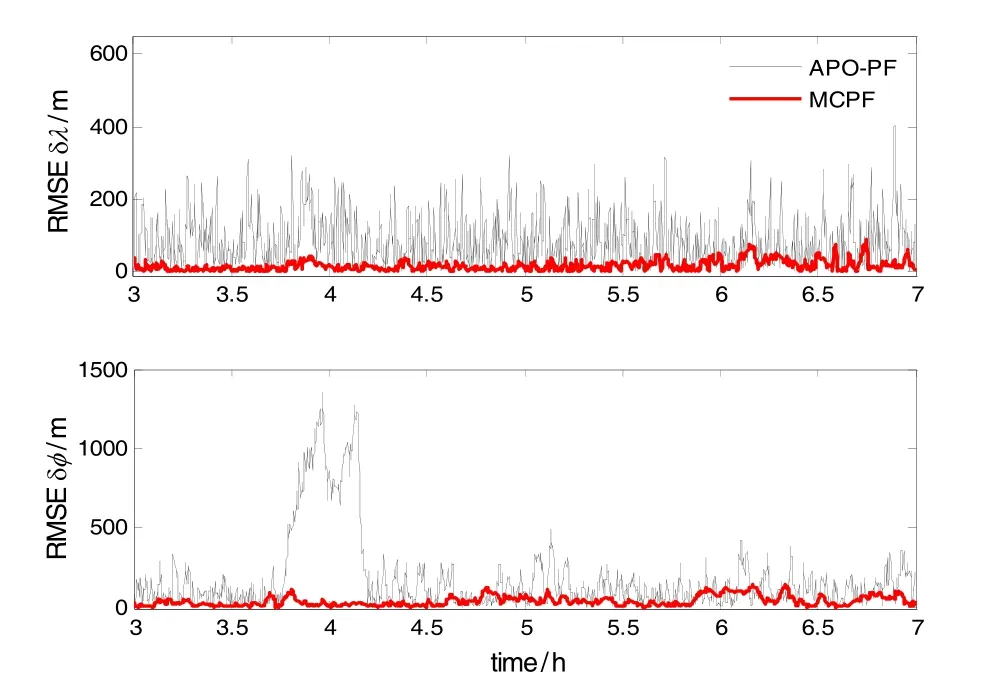
圖4 緯度經度誤差比較Fig.4 Latitude and longitude RMSE comparison

由圖4的經緯度RMSE可以看出，MCPF算法經緯度誤差估計穩定且始終收斂，其精度高于APO-PF算法。同時MCPF單次運行時間為0.0113 s，高于APO-PF單次的0.418 s。

3.2 結果分析

3.2.1 圓概率誤差定位精度分析

常用圓概率誤差(CEP)評定導航定位誤差，定位誤差用到規定點(真實位置或均值)的徑向距離表示，這一誤差稱為圓誤差。根據國軍標GJB729—1989《慣性導航系統精度評定辦法》，船用慣導圓概率誤差(CEP)評定試驗數據通常以50%置信水平選取概率半徑，即R50。它的意義是以真實位置為圓心，包圍全部定位誤差點一半的圓的半徑為 R50，可通過在評定時間內各時刻采樣點上位置誤差的圓概率誤差半徑 Rpj中的最大值 Rp來衡量，即 Rp=max Rpj(1 ≤ j≤ m)。若令：

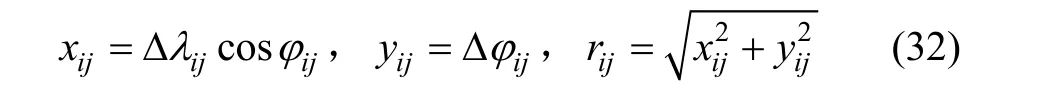
式中，Δ λij、Δ φij表示第i次仿真中第j個時間點的經緯度誤差值， xij、 yij、 rij記作水平、垂直、徑向位置誤差，其中仿真次數 i= 5， j∈[2.7 h, 7 h]，每隔10 s進行一次采樣。

圖5 MCPF 10E2噪聲的CEP曲線圖Fig.5 CEP curve graph of MCPF under noise of 10E2

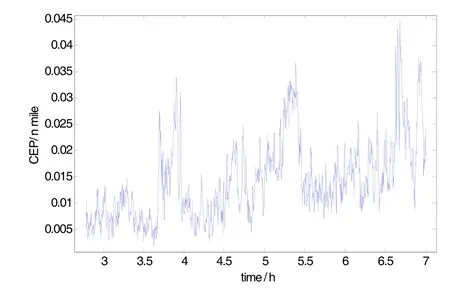
圖6 MCPF 1E2噪聲的CEP曲線圖Fig.6 CEP curve graph of MCPF under noise of 1E2

10 E2和1E2梯度儀噪聲下4 h航跡CEP曲線如圖5和圖6所示。表2對1E2和10E2噪聲下位置誤差進行了比較計算。

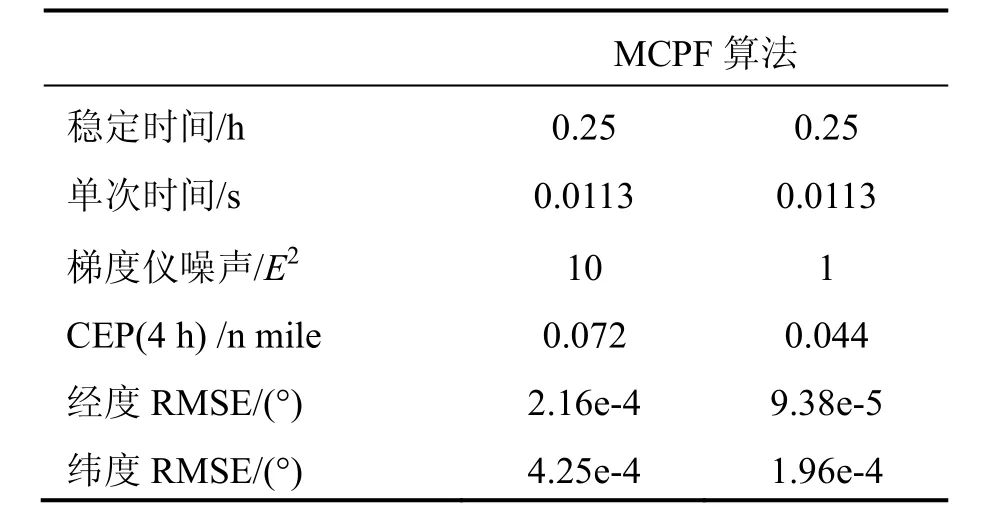
表2 算法結果數值Tab.2 Value of algorithm

從表2可見， MCPF算法對所用數據梯度儀1E2噪聲比10E2噪聲CEP（單位：n mile）[12]及經緯度RMSE都有較大降低。由于使用慣導性能較低，所以當采更高精度的導航儀時，CEP定位精度將會進一步提高。

經緯度以外狀態量的估計可通過 MCPF中的Kalman濾波給出。

3.2.2 定性分析

其余狀態量估計效果也可通過狀態陣簡化進行簡略定性分析。從圖2速度圖像可見，載體近似勻速運動，所以東向和北向加速度計值近似為0，即 ▽Ax≈0，▽Ay≈ 0。為明確可觀測問題，把短時間內(1～2 min)可忽略不計的元素舍棄以簡化系統方程，同時還忽略短時間內地球旋轉和地球表面彎曲，≈03×1，≈03×1。簡化后，狀態轉移陣為：

可見，航向失準角γ不可觀，因為γ所對應列為零。

載體近似直線航行，因此 - gβ與加速度計偏差▽Ax的和以及gα與 ▽Ay的和是可觀測的，即：但可觀測性較低，通過載體速度變化可將兩者估計出來。水平失準角與水平陀螺漂移耦合，通過轉彎，水平失準角與水平陀螺漂移可觀測。

陀螺漂移及水平失準角估計圖像如圖7和圖8所示。

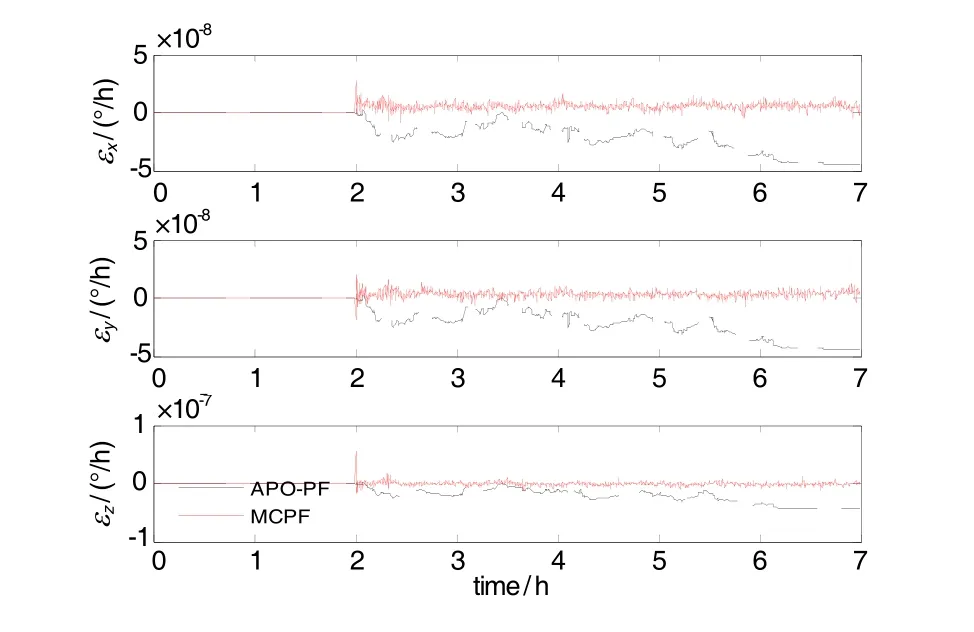
圖7 陀螺漂移RMSE比較Fig.7 Gyro drifts RMSE comparison

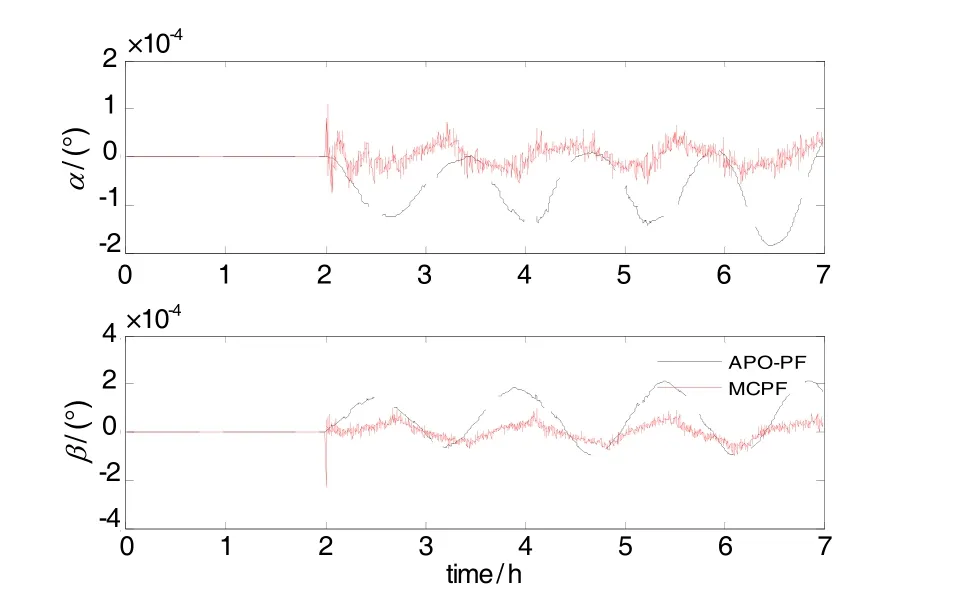
圖8 水平失準角RMSE比較Fig.8 Level misalignment angel RMSE comparison

4 結 論

本文使用能更充分利用地球物理場信息的重力梯度輔助慣性導航，對重力梯度輔助導航的基本原理及各部分組成進行了論述。設計了在圖匹配下的框架圖，并使用新的邊緣CPF算法作為融合算法。從理論上證明了邊緣粒子濾波能夠降低線性狀態估計方差。推導了CKF算法與MPF算法結合的MCPF算法流程，給出系統狀態方程和量測方程，根據量測是經緯度誤差非線性函數特點，狀態方程分解。在較大初始誤差下，計算表明，MCPF在梯度儀1E2和10E2噪聲下，4 h CEP限制在80 m和133 m內。然后通過狀態方程簡化，對其余狀態量估計結果進行了說明。

（References）：

[1] 楊勇，王可東，吳鎮，等. 不同參數對地形等值線匹配算法精度影響的評估分析[J]. 航空學報，2010，31(5)：996-1003.

YANG Yong, WANG Ke-dong, WU Zhen, et al. Evaluation of performance of ICCP algorithm with different parameters[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(5): 996-1003.

[2] Richeson J A. Gravity gradiometer aided inertial navigation within non-GNSS environments[D]. Baltimore: University of Maryland, 2008: 20-32

[3] 王艷東，胡華峰，楊少帥. 重力梯度數據在導航系統中應用[J]. 電光與控制，2013，20(11)：11-15.

WANG Yan-dong, HU Hua-feng, YANG Shao-shuai. The application of gravity gradient data to navigation system[J]. Electro Optics and Control., 2013, 20(11): 11-15.

[4] 劉繁明，錢東，劉超華. 一種人工物理優化的粒子濾波算法[J]. 控制與決策，2012，27(8)：1145-1156.

LIU Fan-ming, QIAN Dong, LIU Chao-hua. An artificial physics optimized particle filter[J]. Control and Decision, 2012, 27(8): 1145-1156.

[5] Brown D, Mauser L, Young B, et al. Atom interferometric gravity sensor system[C]//2012 IEEE Position Location and Navigation Symposium. 2012: 30-37.

[6] 錢東，劉繁明，李艷，等. 導航用重力梯度基準圖構建方法的比較研究[J]. 測繪學報，2011，40(6)：736-744.

QIAN Dong, LIU Fan-ming, LI Yan, et al. Comparison of gravity gradient reference map composition for navigation[J]. Acta Geodaetica et cartographica Sinica, 2011, 40(6): 736-744.

[7] Casella G. Rao-Blackwellisation of sampling schemes[J]. Biometrika, 1996, 83(1): 81-94.

[8] Wang Zong-yuan, Sun Feng. Decentralized estimation of nonlinear target tracking based on nonlinear filter[C] //Proceedings of the 2ndInternational Conference on Mechatronic Science, Electric Engineering and Computer. 2013: 22-26.

[9] Arasaratnam I, Haykin S. Cubature Kalman filter[J]. IEEE Transactions on Automatic Control, 2009, 54: 1254-1269.

[10] Affleck C A, Jircitano A. Passive gravity gradiometer navigation system[C]//1990 IEEE Position Location and Navigation Symposium. 1990: 60-66.

[11] Jircitano A, White J, Dosch D. Gravity based navigation of AUV’s. Proceedings of the symposium on autonomous underwater vehicle technology. Washington, 1990: 177-180

[12] 袁贛南，張紅偉，袁克非，吳簡彤. 基于重力梯度輔助定位的概率神經網絡改進方法[J]. 中國慣性技術學報，2013，21(3)：369-374.

YUAN Gan-nan, ZHANG Hong-wei, YUAN Ke-fei, WU Jian-tong. Improved probabilistic neural network method based on gravity gradient aided location[J]. Journal of Chinese Inertial Technology, 2013, 21(3): 369-374.

邊緣CPF算法及在重力梯度輔助導航中應用

王宗原1,2，孫 楓2

Marginal cubature particle filter and its application in gravity gradient aided navigation

WANG Zong-yuan1,2, SUN Feng2
(1. College of Science, Harbin Engineering University, Harbin 150001, China; 2. College of Automation, Harbin Engineering University, Harbin 150001, China)

INS has large accumulated errors after long journey owing to its inherent reason, which can be decreased by integrating INS with gravity gradient measurement. In this paper, the theory of gravity gradiometer aided INS is described, and its framework chart is presented. Then the gravity map and gradiometer is analyzed, and its measurement equation is set. Based on the feature of state-apace function, a marginal cubature particle filter is proposed to provide estimation in information fusion, and then its variance is proved to be reduced by statistical theory. In addition, the flowchart of algorithm is given, and the simulation is performed. Under the same condition, the position accuracy of the proposed algorithm is higher than that of the existing APO-PF algorithm based on the comparison of their attitude and longitude’s RMSE results. The CEP is used for assessing navigation errors, and it is shown that the gradiometer’s 4 h CEPs under 1E2and 10E2noises are 0.044 n mile and 0.072 n mile, respectively, in low-accuracy inertial navigation system. Finally, the state equation is simplified and used to qualitatively analyze the estimation effect of other state variables.

gradiometer aided inertial navigation system; marginal filter; state decomposition; cubature particle filter; CEP

1005-6734(2014)06-0734-07

10.13695/j.cnki.12-1222/o3.2014.06.007

U666.1

A

2014-07-14；

2014-11-21

中央高校基本科研業務費資助；國家自然科學基金項目（61001154）

王宗原（1977—），男，博士研究生，從事組合導航、非線性濾波研究。E-mail：wangzongyuan@hrbeu.edu.cn

聯 系 人：孫楓（1944—），男，教授，博士生導師。E-mail：w0164@sina.com