宇航級三浮陀螺儀三質量塊隔振模型

（1. 天津航海儀器研究所，天津 300131；2. 北京控制工程研究所，北京 100190）

（1. 天津航海儀器研究所，天津 300131；2. 北京控制工程研究所，北京 100190）

從三浮陀螺儀的結構出發，考慮浮液和動壓氣體軸承的特點及隔振作用，運用振動理論和隔振技術，建立并論述了三浮陀螺儀三質量塊振動模型。對該模型在受迫振動下的運動方程進行了分析，得到了運動方程的解。對該模型的參數進行了識別，對浮液阻尼特性進行了分析，用攝動法求解了阻尼系數c12；對波紋管彈性系數進行了推導計算，得到了彈性系數k12的表達式；對氣體軸承的動態阻尼和剛度進行了分析說明，得到了阻尼系數c23和彈性系數k23的表達式。基于此模型，給出了力傳遞系數的求解方法以及表達式。對三浮陀螺儀振動傳遞研究有一定指導作用。

三質量塊模型；振動方程；阻尼；彈性系數；力傳遞系數

宇航三浮陀螺儀工作過程中存在復雜和嚴酷的力學環境條件，其環境試驗條件包括振動、沖擊載荷、熱真空等。三浮陀螺儀由于浮子處在中性懸浮狀態，在大過載作用下，雖然浮液起到一定隔振作用，但外界載荷過大依然會對陀螺儀核心部件浮子內部高速旋轉的電機產生破壞作用，如果振動量級過大將影響陀螺儀電機正常工作，導致陀螺儀故障。鑒于惡劣的使用環境會對三浮陀螺儀的工作穩定性和精度產生影響，為了確保宇航三浮陀螺儀在各種環境下的正常工作，對其進行振動傳遞技術的研究很有必要。近年，星箭力學環境分析與試驗技術研究的進展迅猛，早在上世紀末國外就對整星進行隔振研究[1-3]，目前國內主要集中在對關鍵部件的局部減振上，如慣性平臺減振器[4]等。三浮陀螺儀作為慣性平臺上的關鍵器件，國內外可查的振動研究資料較少，因此對其進行振動技術研究很有必要。

1 三浮陀螺儀振動模型

1.1 三質量塊模型

三浮陀螺儀主要由殼體、浮液、波紋管部件、磁懸浮部件、浮子、電機等組成，結構簡圖如圖1所示。該三浮陀螺儀系統可簡化為三質量塊兩自由度系統。三質量塊兩自由度模型在各種隔振系統的建模中起著非常重要的作用。由于浮液和動壓氣體軸承的特點及隔振作用，這種模型同單質量塊以及二質量塊模型相比較，三質量塊模型參數更適合表征三浮陀螺儀系統[5]。[1]。

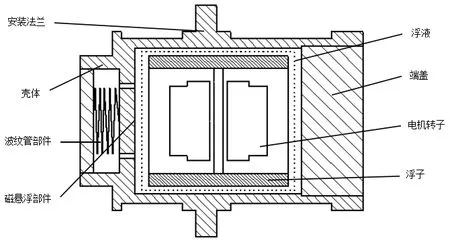
圖1 陀螺儀結構簡圖Fig.1 Schematic diagram of floated gyro

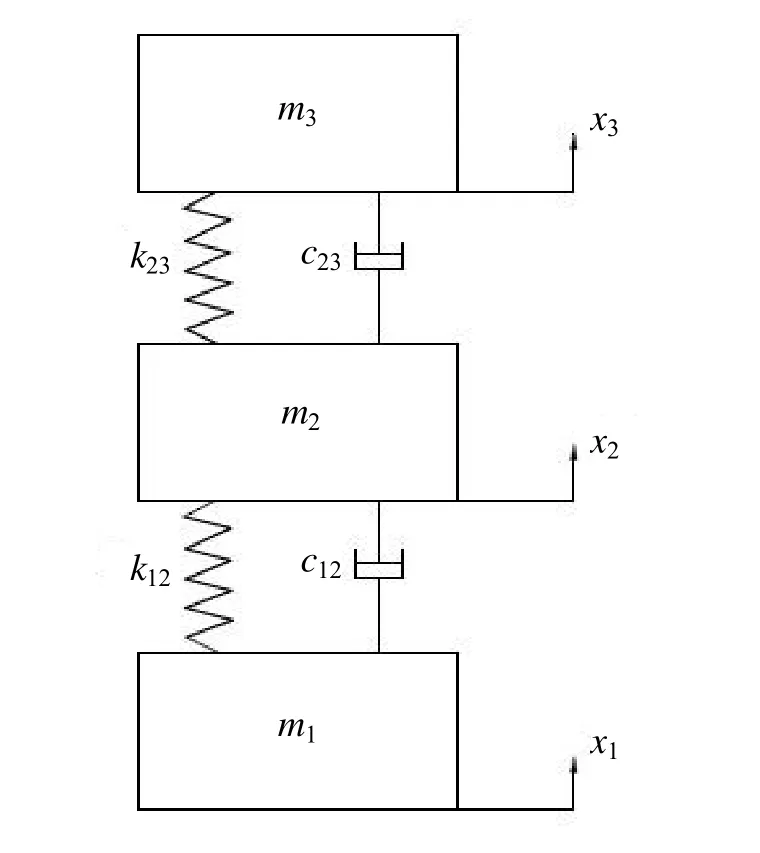
圖2 三質量塊模型 Fig.2 Three-mass model of the floated gyro

三浮陀螺儀存在三個軸向的線振動，分別為SA(自轉軸)、IA(輸入軸)、OA(輸出軸)方向。其中SA、IA方向陀螺儀的結構幾乎完全相同，屬于同一模型，即本文討論的單軸三質量塊線振動模型；z方向與 x和y方向相比只是結構參數在取值上不同，同樣適用于單軸三質量塊模型。為了便于建立線振動方程進行理論研究，此文將其簡化為線性離散系統，屬于集總參數線性系統。

對于很多系統，連續的質量離散后不影響最終分析結果，這種簡化是合理的。三浮陀螺儀三質量塊線振動模型的三個質量塊分別為殼體、浮子、電機轉子，如圖2所示。圖2中 m1、 m2、 m3分別表示陀螺儀殼體中心處、浮子中心處質量(此處假設浮子內部質量分布均勻)、電機轉子中心處質量。浮液及波紋管組合表示為彈性元件與黏性阻尼器的并聯，彈性系數為 k12，阻尼系數為 c12；這部分是該模型的第一個隔振單元，起到主要的隔振作用。軸承與轉子間的動壓氣體軸承的動態特性與電機轉子的動力學行為有直接關系，影響轉子臨界轉速、不平衡響應以及轉子穩定性。氣體軸承的動態特性可以用其氣膜的動態彈性系數和動態阻尼系數來表征，表示為有一定彈性系數和阻尼作用的隔振器，彈性系數為 k23，阻尼系數為 c23；這部分是該模型的第二個隔振單元。假設殼體、浮子、電機轉子的相對位移分別為 x1、x2、x3。環境試驗條件下，外界的振動直接施加在殼體 m1上；然后通過彈性系數為 k12、阻尼系數為 c12的隔振元件，振動能量傳遞到浮子 m2上；再經過彈性系數為 k23、阻尼系數為 c23的氣體軸承，把能量傳遞到電機轉子上。

1.2 三浮陀螺儀振動方程

由三質量塊線振動模型，依據振動理論[6]建立運動方程:

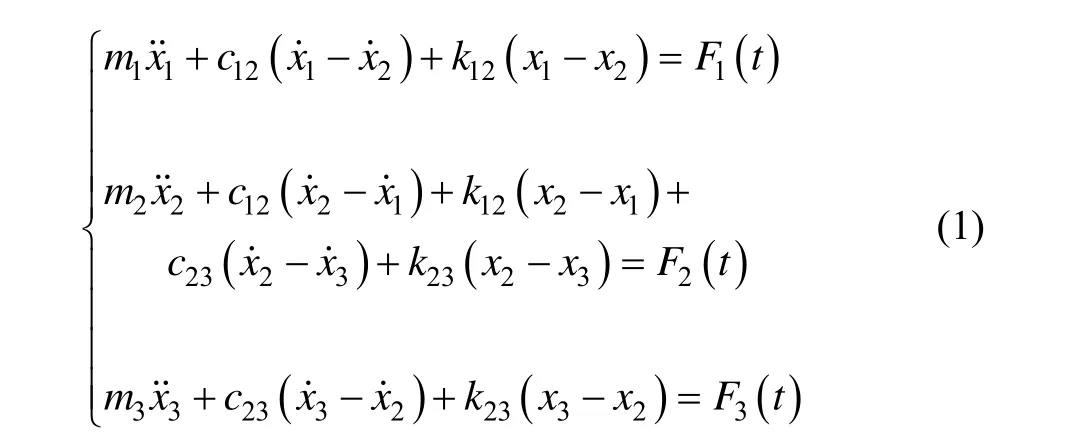
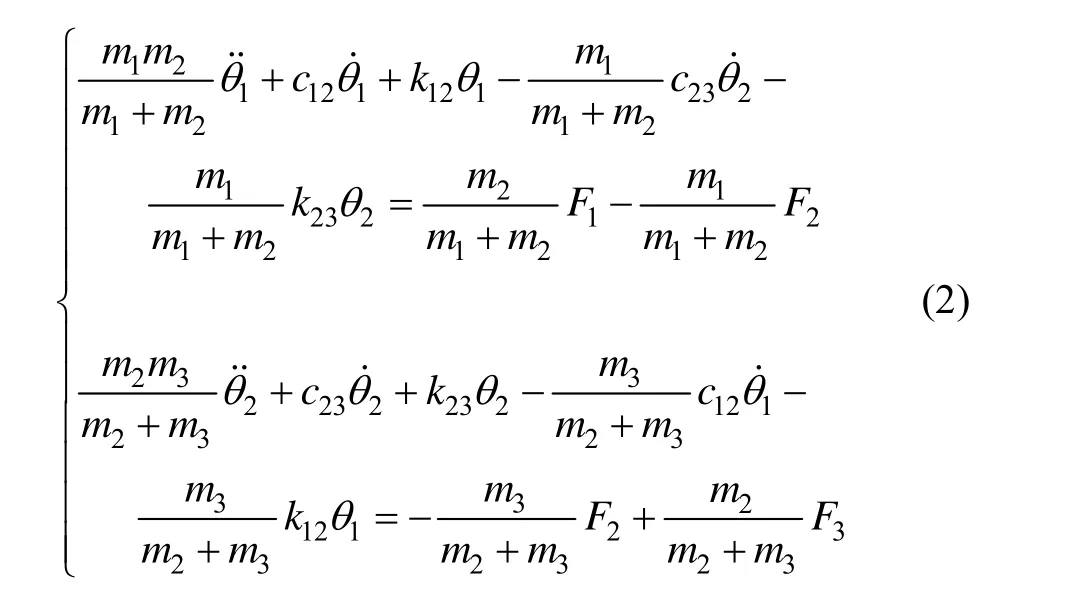
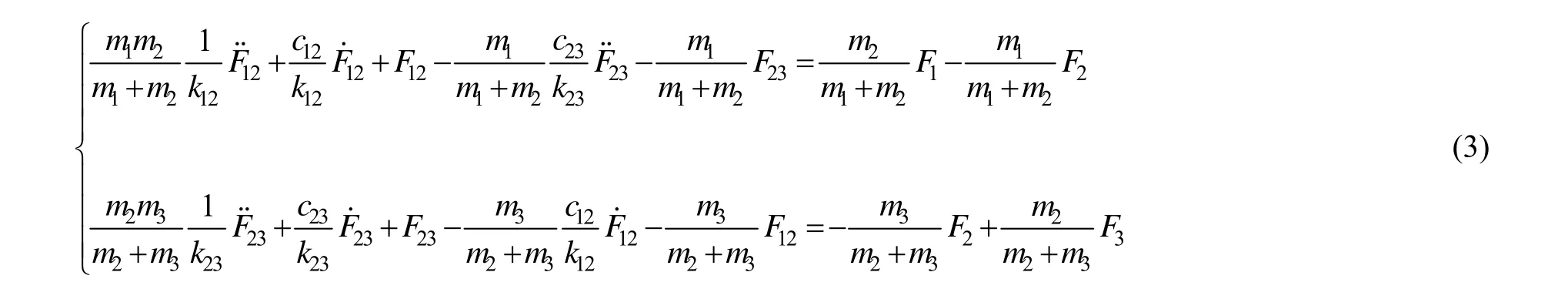
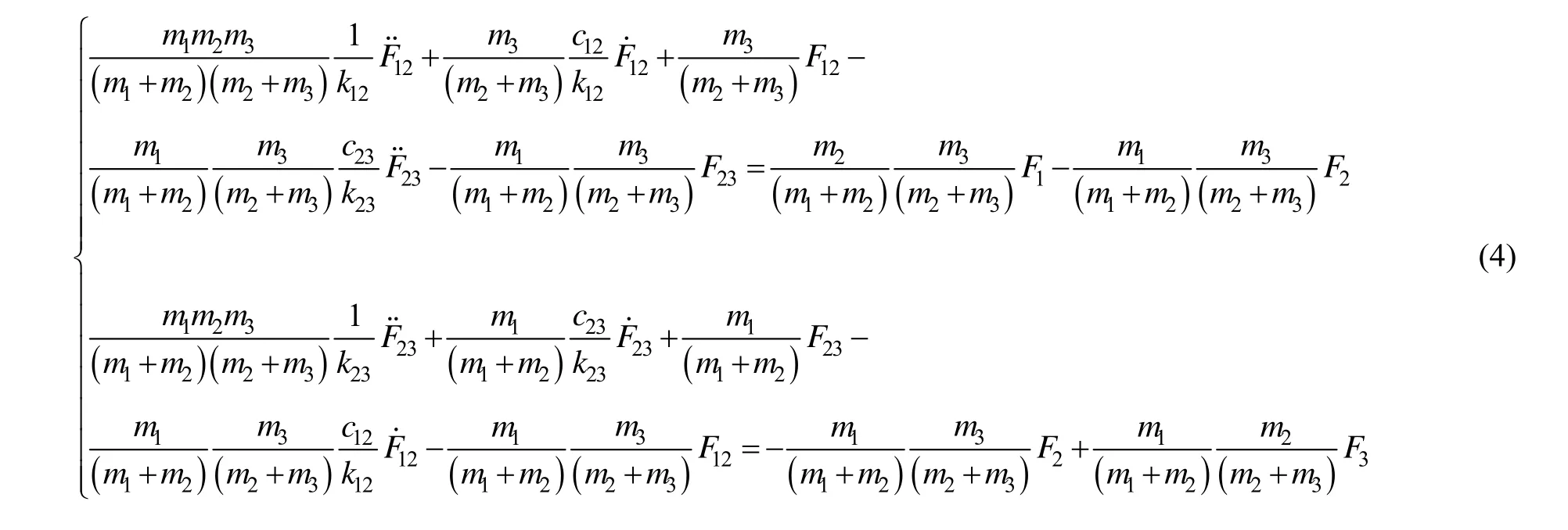
為了簡化方程，引入下列標記：

廣義質量：

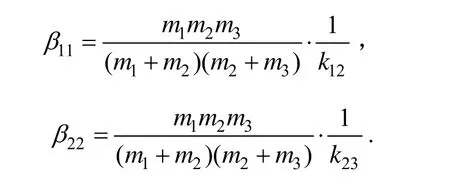
廣義彈性系數：

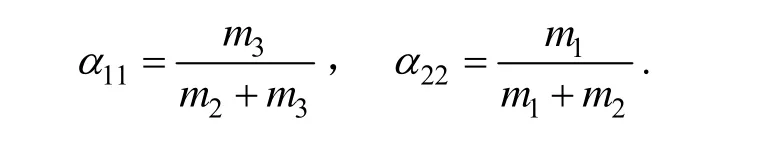
彈性耦合系數：

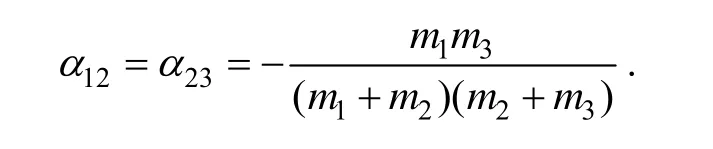
廣義阻尼系數：

阻尼耦合系數：

廣義激勵力：

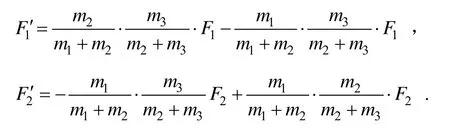
簡化后得方程：

對于受迫振動，為了確定所受激勵力的響應，將式(5)轉換成正則坐標和表示的方程。以激勵力作為坐標，該系統的Lagrange函數可以寫成中：L是總能，T是動能，V是勢能；α ,β是正則坐標中的廣義彈性系數和慣性。

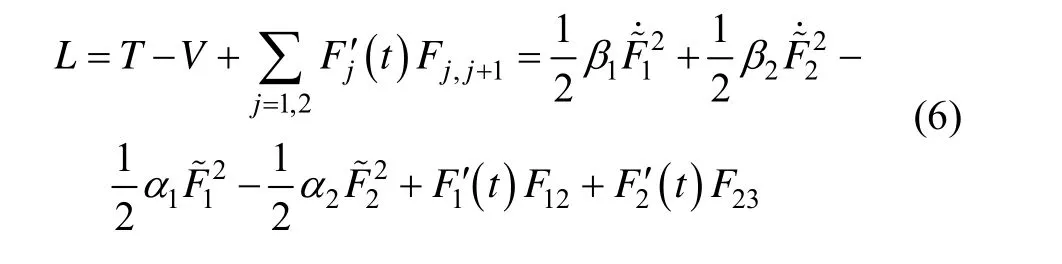
系統的Lagrange運動方程為

由此可得受迫振動時有阻尼形式的運動方程：

式中： Δ1、Δ2是該系統的相對阻尼系數， K1、K2是彈性力分布系數。

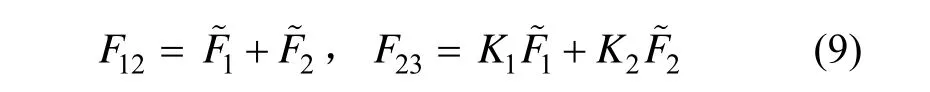
2 三浮陀螺儀隔振參數識別

2.1 阻尼系數c12、c23

宇航級三浮陀螺儀浮液選用高比重氟油，相對密度較高，在工作溫度下密度可達2 g/cm3。其中浮液除了起重力卸載作用外，還利用其高黏度，使浮子與殼體之間產生粘切力矩形成對浮子運動的阻尼。浮子和殼體之間充滿的浮液，還起到油膜阻尼作用，通過振動產生擠壓油膜阻尼作用消耗振型和振動的能量，對振動起到顯著的抑制作用，從而提高系統的整體抗振性能[5]，同時減小寶石軸承產生的摩擦力矩，提高陀螺儀精度。

本文提出假設：1）正負擠壓過程無空穴現象；2）振幅比油膜靜態厚度小得多；3）大過載力作用時，認為浮子存在微小的擺動和微小的圓旋運動。

前兩個假設保證油膜呈線性阻尼作用。試驗研究表明，振動對油膜產生正向和負向的擠壓作用，在無空穴效應條件下，油膜產生的阻尼作用表現為線性阻尼。依據流體動力學理論，建立不可壓縮流體常粘性三維層流問題的Reynolds方程：

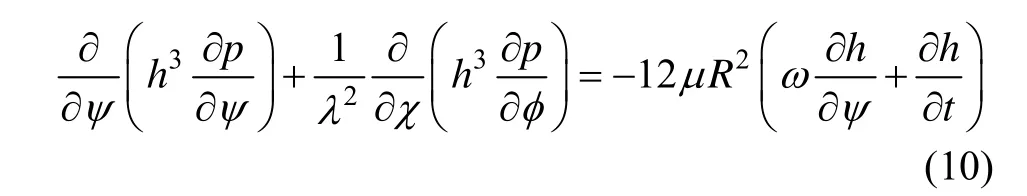
式中： hc為浮液厚度，A為振動體擺動角的幅值。

聯立(10)(11)按攝動法解微分方程。當對腔體內任意點處壓力 p(χ,ψ)作零次近似和一次近似時，圓旋運動引起浮液的阻尼力矩為零，二次近似阻尼力矩和一次近似結果完全一致；更高階近似情況下是非線性阻尼。因此，對于微小圓旋運動引起的液體阻尼在本論文中不作考慮。僅考慮正負擠壓作用下的阻尼系數。由以上方程聯合邊界條件求得一次近似阻尼系數為：

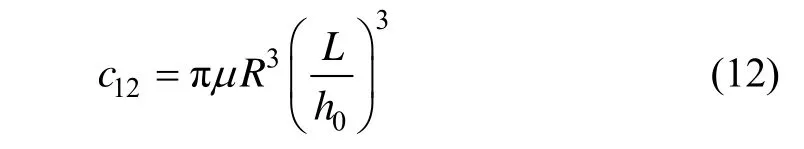
以上阻尼系數 c12是依據液體動力學的 Reynolds方求得。由液體動力學與氣體動力學方程的一致性，可求得阻尼系數 c23。

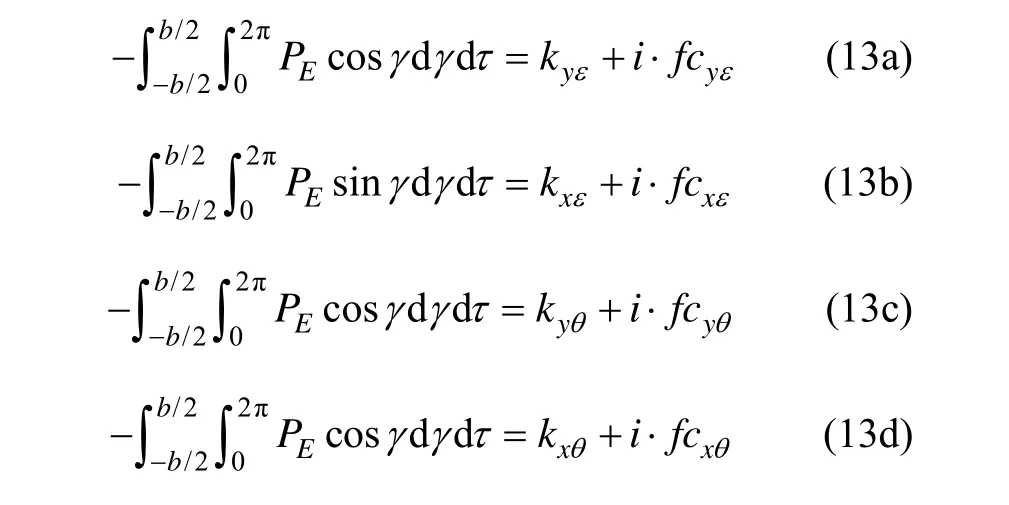
式(13)求得的阻尼系數在直接坐標系中表示為：

式中，ξ為擾動下轉子的偏移角。

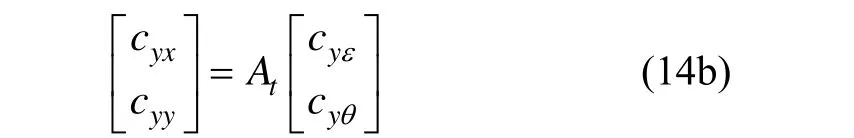
則阻尼系數：

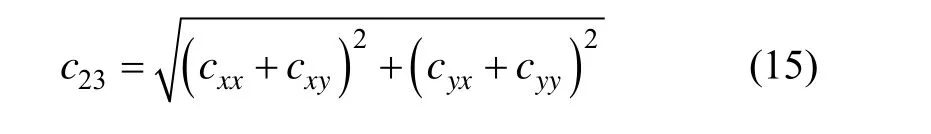
2.2 彈性系數k12、k23

浮液作為一層不可壓縮的阻尼膜，充滿殼體和浮子之間很小的間隙。振動過程中浮液受到擠壓發生流動，受擠壓的液體流向波紋管。波紋管發生變形，起到緩沖作用。波紋管彈性系數相比殼體小很多，因此把殼體看作剛性的，只考慮波紋管的彈性系數。此處，波紋管相當于彈性系數為 k12的彈簧，假設每個卷曲的彈性系數為k′，共有n個卷曲組成，則：

馬達定、轉子之間氣體軸承的彈性系數分為靜態彈性系數和動態彈性系數。陀螺儀不受外力干擾，當陀螺儀H軸處于向下位置時，指軸向靜態彈性系數；當陀螺儀H軸處于水平位置時，指徑向靜態彈性系數。

靜態時：

式中， Δδ 為轉子軸向或徑向的位移差。

當陀螺儀受到外力作用時，氣體軸承的動態彈性系數可由式(13)求得。轉換為直接坐標形式如下：

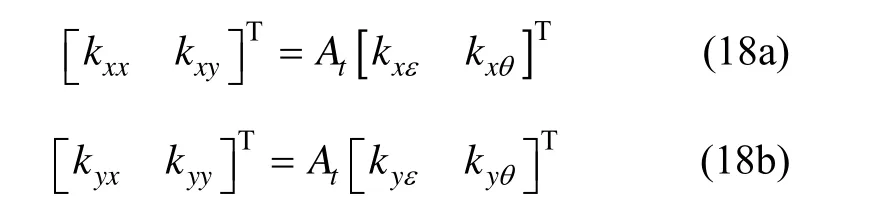
動態時：

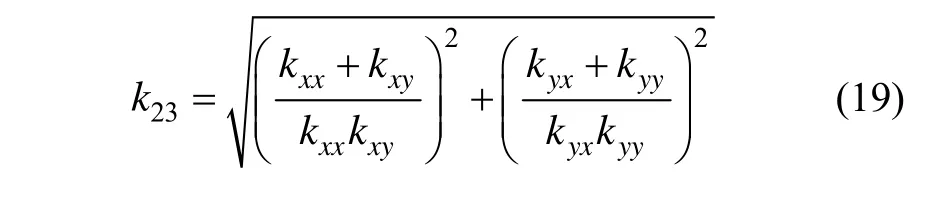
3 三浮陀螺儀在簡諧激勵力下振動傳遞系數

假設系統在頻率為ω、振幅為 F0的簡諧激勵下作強迫振動。依據建立的振動方程得：

令θ3= x3- x1，得:

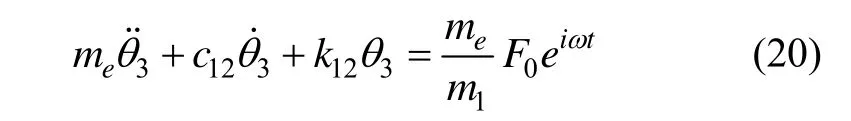
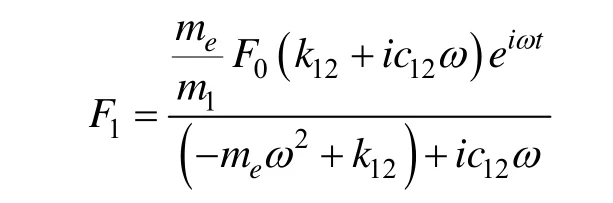
由此可得絕對力傳遞系數：

由此可知，力傳遞系數 μF與系統所受激勵頻率、阻尼比及對數衰減率有關。

4 結 論

對浮液阻尼特性和波紋管彈性系數進行了推導計算。對氣體軸承的動態阻尼和動態彈性系數進行了分析說明。初步建立了三浮陀螺儀振動傳遞理論方程，推導了力傳遞系數，對相關試驗有理論指導作用。為分析三浮陀螺儀宇航環境條件下動力學特性提供了有力的理論支持。

本文僅對模型做了理論分析，還需開展相關試驗說明三浮陀螺儀在200～2000 Hz內及多大的能量下，可以適應宇航的沖擊、振動條件。非線性[7]對三浮陀螺儀系統的影響也有待深入研究。

（References）：

[1] 馬興瑞，于登云，韓增堯，等. 星箭力學環境分析與試驗技術研究進展[J]. 宇航學報 2006，27（3）：323-331.

MA Xing-rui, YU Deng-yun, HAN Zeng-yao, et al. Research evolution on the satellite-rocket mechanical environment analysis and test technology[J]. Journal of Astronautics, 2006, 27(3): 323-331.

[2] SHI Huai-Long, LUO Ren, WU Ping-Bo, ZENG Jing, et al. Application of DVA theory in vibration reduction of carbody with suspended equipment for high-speed EMU[J]. Science China (Technological Sciences), 2014, 57(07): 1425-1438.

[3] Hyun-Ung Oh, Kyung-Joo Lee, Mun-Shin Jo. A passive launch and on-orbit vibration isolation system for the spaceborne cryocooler[J]. Aerospace Science and Technology, 2013, 28(1): 324-331.

[4] 王旭，張嶸. 慣性導航系統并聯緩沖器動力學分析與仿真[J]. 中國慣性技術學報，2013，21(5)：561-569.

WANG Xu, ZHANG Rong. Dynamical analysis and simulation of parallel bumper for INS[J]. Journal of Chinese Inertial Technology, 2013, 32(9): 1113-1117.

[5] QIAN De-jin, YAO Xiong-liang. Impeding vibration wave propagation from several arranged vibration isolation masses[J]. Applied Acoustics, 2009, 28(5): 321-329.

[6] 朱時堅，樓京俊，何其偉，翁雪濤. 振動理論與隔振技術[M]. 北京：國防工業出版社，2008：147-179.

[7] WANG Qiang-yong, LU You-min, WANG Xian-zhong, et al. Study on the impediment to vibration wave propagation from rigid vibration isolation mass[J]. Journal of Marine Science and Application Rigid Vibration Isolation Mass, 2011, 10(1): 63-69.

[8] 戚社苗，耿海鵬，虞烈. 動壓氣體軸承的動態彈性系數和動態阻尼系數[J]. 機械工程學報，2007，43(5)：91-98.

QI She-miao, GENG Hai-peng, YU Lie. Dynamic stiffness and dynamic damping coefficients of aerodynamic bearings [J]. Chinese Journal of Mechanical Engineering, 2007, 43(5): 91-98.

[9] Tang B, Brennan M. A comparison of the effects of nonlinear damping on the free vibration of a singledegree-of-freedom system[J]. Journal of Vibration and Acoustics, 2012, 134(2): 024501.1-014501.4.

宇航級三浮陀螺儀三質量塊隔振模型

韋俊新1，劉志宏1，孫 麗2，孫學成1，田 勇1

Three-mass vibration isolation model of astronautical three-floated gyro

WEI Jun-xin1, LIU Zhi-hong1, SUN Li2, SUN Xue-cheng1, TIAN Yong1
(1. Tianjin Navigation Instrument Research Institute, Tianjin 300131, China; 2. Beijing Institute of Control Engineering, Beijing 100190, China)

According to the physical structure of the floated gyro and considering the vibration-isolation effect of the viscous liquid and aerodynamic bearings, a three-mass model of three-floated gyro is established and discussed based on the vibration theory vibration-isolation technique. The motion equations under forced vibration are analyzed and solved. The parameters of the model are identified, the damp c12is got in the method of perturbation, and the damp c23, stiffness k12and k23are given. Based on the proposed model, the solution to the modulus of force transmission is obtained. These analyses could provide reference for the research of three-floated gyro’s vibration transmission.

three-mass modal; vibration equations; damper; stiffness; modulus of force transmission

1005-6734(2014)06-0815-05

10.13695/j.cnki.12-1222/o3.2014.06.021

U666.1

A

2014-11-14；

2014-10-23

國防科技重點預研項目（51309050102）

韋俊新（1966—），男，研究員，碩士生導師，從事慣性元件研究。E-mail：weijunxin@aliyun.com