斜直井段套管-水泥環(huán)組合系統(tǒng)受力特性分析

王宴濱，高德利，房 軍

(中國石油大學石油工程教育部重點實驗室，北京 102249)

對于直井段套管－水泥環(huán)－地層組合系統(tǒng)的受力特性問題已做過大量的研究，為正確認識套損問題提供了豐富的依據(jù)［1-5］，然而實際情況中存在著大量的斜直井段，理論上的直井在實際中也不可能是絕對的垂直井，總存在一定的井斜角［6］，因此將直井段得出的規(guī)律應用在斜井段時受到了限制。筆者采用坐標變換的方法從理論上研究斜直井條件下套管－水泥環(huán)－地層組合系統(tǒng)的受力特性，以得到斜井段下套管的外擠力分布，為正確認識斜井段套管的損壞問題及采取合理的預防套損措施提供參考。

1 應力張量的坐標變換與分解

1.1 應力張量的坐標變換

在油田地應力分析中，通常將地應力用3個主應力表示，即上覆巖層壓力σv、最大水平主應力σH和最小水平主應力σh。σv的方向為豎直向下，而σH和σh在不同的地域方向不同，且通常使用井壁崩落法、巖心差應變試驗、水力壓裂法等方法進行測量［7-8］。

選擇初始坐標系(X，Y，Z)分別與主地應力σH、σh和 σv方向相反，并建立直角坐標系(x1，y1，z1)、(x，y，z)和(r，θ，z)，其中 oz軸對應于井眼軸線方向，ox和oy位于與井眼垂直的平面內(nèi)，如圖1所示。

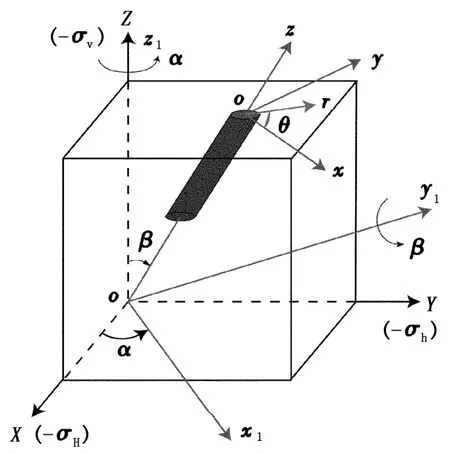
圖1 斜井-直井井軸坐標變換圖Fig.1 Coordinate transformation of inclined-vertical well shaft

為了建立(x，y，z)坐標系與(X，Y，Z)坐標系之間的轉(zhuǎn)換關系，將(X，Y，Z)坐標系按以下方式［7-8］旋轉(zhuǎn):

(1)先將坐標系(X，Y，Z)以Z為軸，按右手定則旋轉(zhuǎn)角度α，變?yōu)?x1，y1，z1)坐標系。α為井斜方位角，指井眼軸線在水平面上的投影與正北方向的夾角。

(2)再將坐標系(x1，y1，z1)以 y1為軸，按右手定則旋轉(zhuǎn)角度β，變?yōu)?x，y，z)坐標系。β為井斜角，指井眼軸線與鉛垂線之間的夾角。

則坐標系(x，y，z)與初始坐標系(X，Y，Z)之間的坐標轉(zhuǎn)換關系為

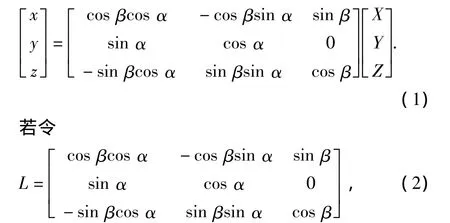
則新坐標系下的地應力張量與原地應力之間的關系為

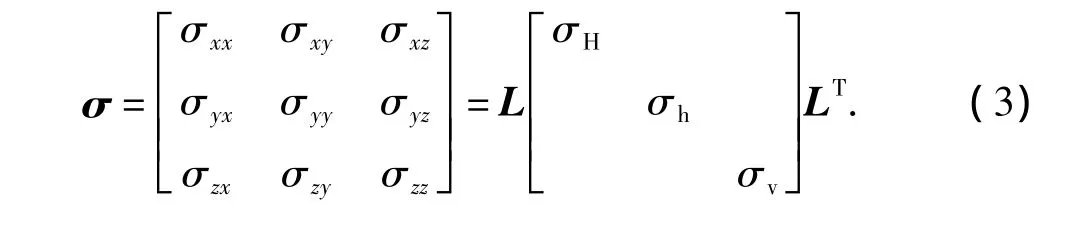
1.2 應力張量的分解

地層中一定深處的套管，其縱向變形受到限制，如不考慮外載(地應力)沿縱向的變化可將此問題處理成平面應變問題加以分析［3］，如圖2所示。因此可以忽略應力張量σ沿z軸方向的分量，得新的應力張量T，即

并將T作如下分解:

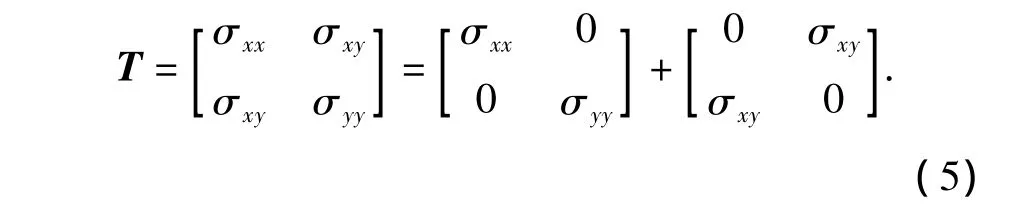
分別令

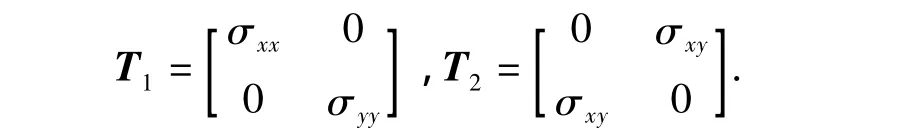
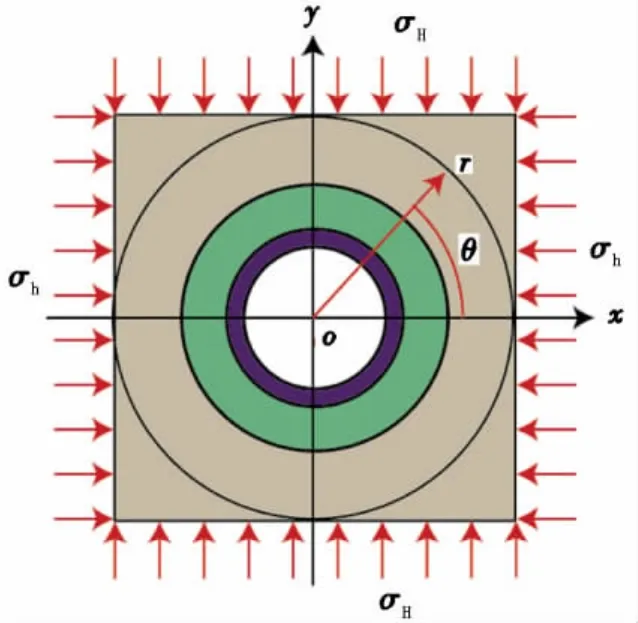
圖2 套管-水泥環(huán)-地層系統(tǒng)平面應變分析模型Fig.2 Plane strain analysis model of casing-cement ring-formation

對于T1，分析方法與垂直井眼在水平主應力作用下的分析相同，具體推導見文獻［3］。

對于T2，轉(zhuǎn)換成極坐標系下的應力表達式為

式(6)與垂直井下的表達式不同，因此須以此應力張量為邊界條件對系統(tǒng)受力進行新的分析計算。

在得到T1和T2兩個應力邊界條件下的套管的外擠特性之后，將其疊加即可得斜直井地層－水泥環(huán)－套管系統(tǒng)在原場地應力下的套管外擠力。

2 套管外擠力響應

2.1 系統(tǒng)在T1下的套管外擠力響應

系統(tǒng)在T1應力下的外擠力響應與垂直井在兩向水平主應力作用下的分析相同，參見文獻［3］。

2.2 系統(tǒng)在T2下的套管外擠力響應

考慮到地層遠場應力的邊界條件(σr=σxysin(2θ))的形式，取應力函數(shù)形式為

式中，φ應滿足應力協(xié)調(diào)方程，因此待定函數(shù)f(r)應滿足

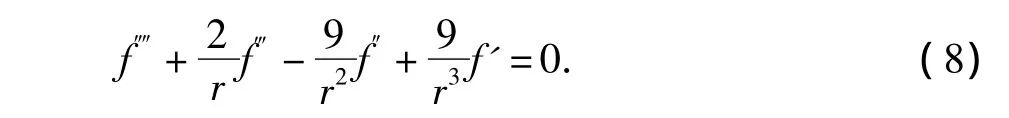
式(8)為一個四階歐拉常微分方程，其通解為

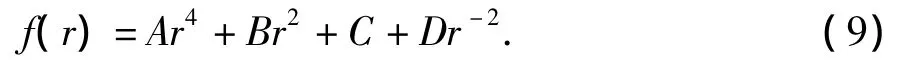
即

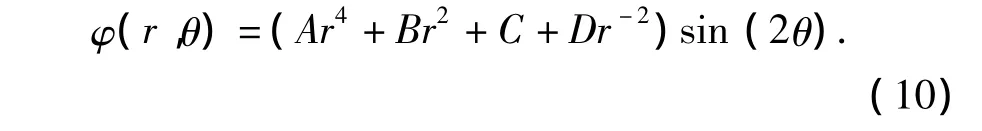
將式(10)代入極坐標系下基本方程，并分別以下標i=1，2，3表示套管、水泥環(huán)、地層，可得到系統(tǒng)在T2下的套管外擠力表達式為

式(11)中共有12個未知參數(shù)，需要12個方程才能求解。其中應力邊界條件和連續(xù)條件與T1類似，可得6個方程［3］，唯一不同在于地層外邊界上的應力邊界條件:

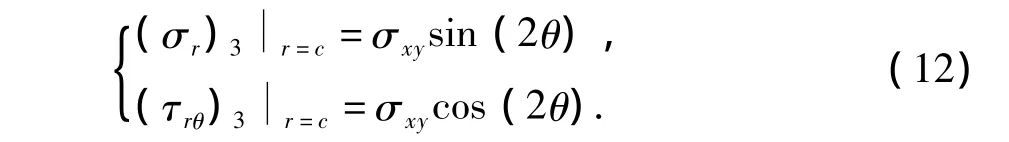
將上述8個應力邊界條件代入式(11)可以得到8個方程，另外4個位移連續(xù)條件需要經(jīng)過位移分析后由位移連續(xù)條件確定。經(jīng)位移分析之后，得到在T2應力場作用下系統(tǒng)的位移方程可表述為

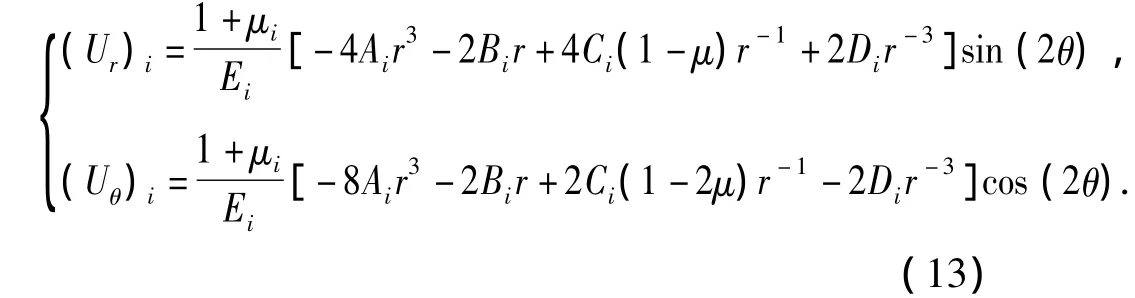
聯(lián)立各應力邊界與連續(xù)條件以及位移連續(xù)條件可得到12個方程，能夠唯一確定式(11)中的12個未知量。

方程的矩陣形式為

其中

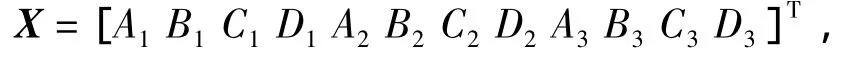
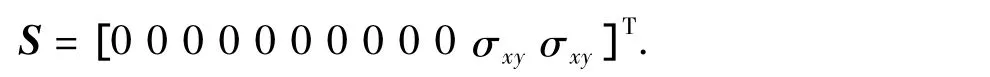
A是與系統(tǒng)各力學參數(shù)及幾何參數(shù)有關的物理量，求解式(14)得到系數(shù)X，將得到的計算系數(shù)代入式(11)即可得到系統(tǒng)在應力場T2下的應力分布。

3 算例分析

參考某油田1.0 km深處地層情況的計算結(jié)果［3，11］。具體參數(shù)為:套管直徑 139.7 mm，壁厚7.72 mm，水泥環(huán)厚度50 mm;地層計算厚度取3.0 m;力學參數(shù)取 E1=2.1 ×105MPa，μ1=0.25，E2=1.1 ×104MPa，μ2=0.25，E3=2.8 × 104MPa，μ3=0.30，方位角30°。計算的地層3個主應力間的關系見表1。

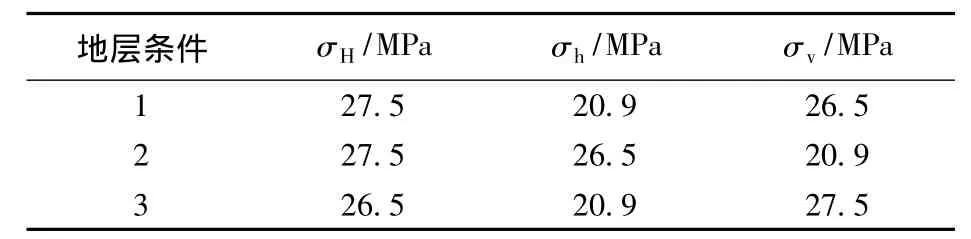
表1 3種條件下地層主應力Table 1 Three cases of formation principal stress

以井斜角30°為例，得到的地層1條件下套管－水泥環(huán)及水泥環(huán)－地層兩接觸表面的接觸應力如圖3所示，為了計算不同井斜角對套管－水泥環(huán)表面接觸應力的影響，在其余條件不變的情況下，將井斜角由0°逐漸增加到90°，即在井由直井逐漸變化到水平井過程中，得到的3種地層條件下套管－水泥環(huán)表面的接觸應力與井斜角的關系分別如圖4所示。

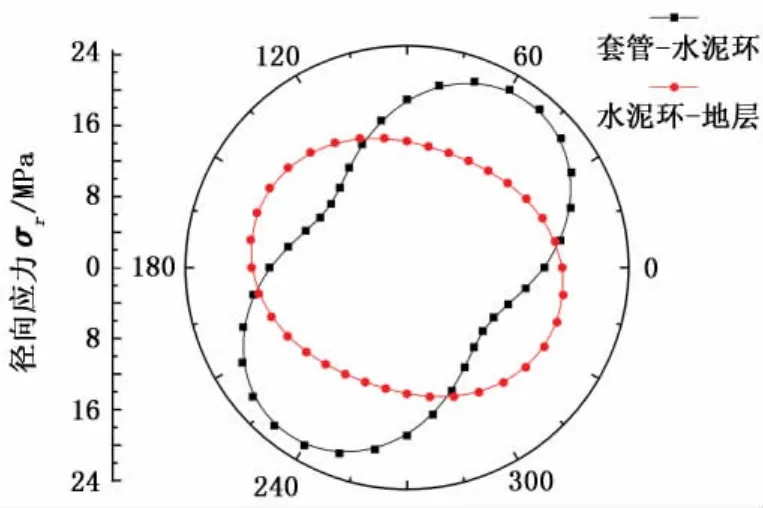
圖3 地層1條件下兩接觸表面的應力分布Fig.3 Stress distribution of two contact surfaces in formation 1

從圖3中可以看出，本算例中在地層1條件下套管－水泥環(huán)界面與水泥環(huán)－地層界面的接觸應力均呈橢圓形分布，并且前者應力分布的非均勻性要大，對套管的安全不利，兩者的應力幅值出現(xiàn)的相位差約為50°。

從圖4可以看出，本算例中3種地層條件下的套管－水泥環(huán)界面接觸應力分布規(guī)律各不相同，原因在于3種地層條件下地層3個主應力間的關系不同。地層1與地層3條件下井斜角從0°變化到90°時，套管外表面徑向應力的非均勻性逐漸減小，套管的抗外擠能力逐漸增強，即在這種地層條件下水平井的套管抗外擠能力要大于同等條件下直井的套管抗外擠能力;地層2條件下，井斜角從0°變化到90°時，套管外表面徑向應力的非均勻性逐漸增大，套管的抗外擠能力逐漸降低，即在這種地層條件下水平井的套管抗外擠能力要小于同等條件下直井的套管抗外擠能力。

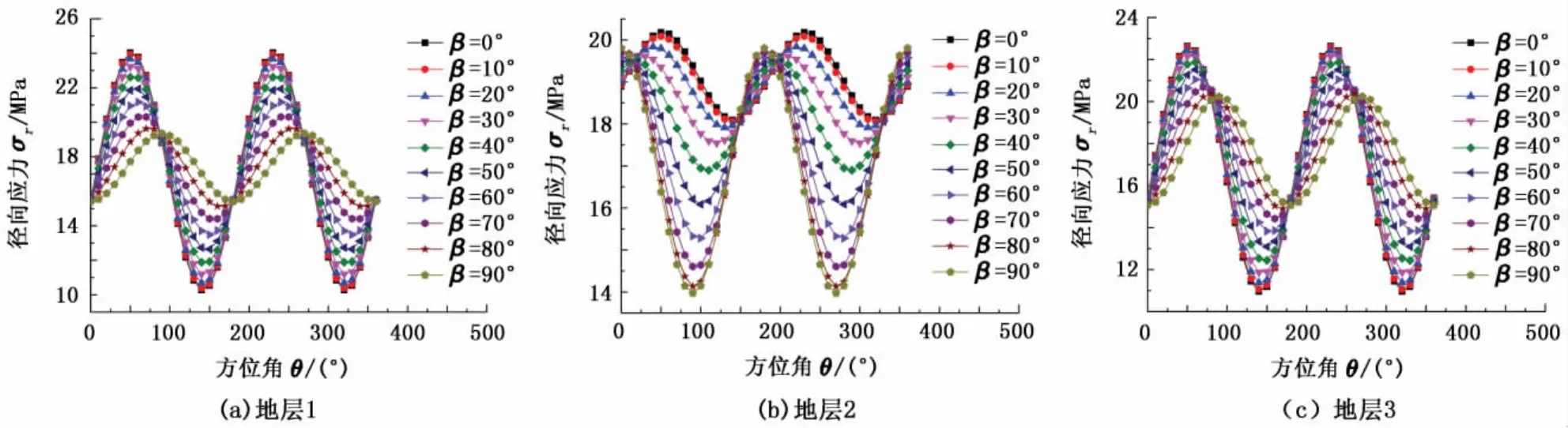
圖4 套管-水泥環(huán)界面應力隨井斜角的變化Fig.4 Variation of stress distribution on casing-cement surface with inclined angle

4 結(jié)論

(1)通過坐標變換將地層的3個主應力變換到斜直井軸線方向與垂直于井眼軸向的平面所確定的坐標系上，可用來分析斜井條件下套管－水泥環(huán)－地層組合系統(tǒng)的受力特性。

(2)地層3個主應力大小關系不同時得到的斜直井下套管－水泥環(huán)界面的徑向接觸應力隨井斜角的變化規(guī)律不同，在某些地層下水平井的套管抗外擠能力要大于同等條件下直井的套管抗外擠能力，而在另一些地層下直井的套管抗外擠能力要大于同等條件下水平井的套管抗外擠能力。

［1］ KHALAF F，CARIO U.Increasing caing collapse resistance against salt-induced loads［R］.SPE 13712，1985.

［2］ EI-SAYED A H，KHALAF F，CARIO U.Resistence of cemented concentic casing string under nonuniform loading［R］.SPE 17927，1989.

［3］ 房軍，趙懷文，岳伯謙，等.非均勻地應力作用下套管與水泥環(huán)的受力分析［J］.石油大學學報:自然科學版，1995，19(6):52-57.FANG Jun，ZHAO Huai-wen，YUE Bo-qian，et al.A-nalysis of sheath loading property of casing and cement under nonuniform geologic stress［J］.Journal of the University of Petroleum，China(Edition of Natural Science)，1995，19(6):52-57.

［4］ 房軍，岳伯謙，趙懷文，等.非均勻地應力作用下套管和水泥環(huán)表面受力特性分析［J］.石油大學學報:自然科學版，1997，21(1):46-48.FANG Jun，YUE Bo-qian，ZHAO Huai-wen，et al.analysis of surface loading on casing and cement sheath under nonuniform geologic stress［J］.Journal of the Uniuersity of Petroleum，China(Edition of Natural Science)，1997，21(1):46-48.

［5］ 房軍，谷玉洪，米豐珍.非均勻載荷作用下套管擠壓失效數(shù)值分析［J］.石油機械，1999，27(7):34-37.FANG Jun，GU Yu-hong，MI Feng-zhen.A numerical analysis of casing collapse under nonuniform load［J］.China Petroleum Machinery，1999，27(7):34-37.

［6］ 高德利，劉希圣，徐秉業(yè).井眼軌跡控制［M］.東營:石油大學出版社，1994.

［7］ 陳勉，金衍，張廣清.石油工程巖石力學［M］.北京:科學出版社，2008.

［8］ 郭春華.井眼應力分布模擬及井壁穩(wěn)定性研究［D］.成都:成都理工大學環(huán)境與土木工程學院，2011.GUO Chun-hua.Simulation of in-situ stress near wellbore and research on wellbore stability［D］.Chengdu:Environment and Construction Engineering Institute of Chengdu University of Technology，2011.

［9］ 李志明，殷有泉.油水井套管外擠力計算及其力學基礎［M］.北京:石油工業(yè)出版社，2006.

［10］ 徐芝綸.彈性力學:上冊［M］.北京:人民教育出版社，1978.

［11］ 李宏，謝富仁，王海忠，等.烏魯木齊市斷層附近地應力特征與斷層活動性［J］.地球物理學報，2012，55(11):3695-3696.LI Hong，XIE Fu-ren，WANG Hai-zhong，et al.Characteristics of in-situ stress measurements near the fault and fault activity in Urumqi city［J］.Chinese Journal of Geophysics，2012，55(11):3695-3696.