基于滑模的艦艇無人直升機懸停控制

侯志寧，顏富強，鄧志雄，王 婕

（1. 天津航海儀器研究所，天津 300131；2. 92330部隊裝備部，青島 266100；3. 海南三亞市91458部隊，三亞 572021；4. 河北工業大學控制科學與工程學院，天津 300130）

基于滑模的艦艇無人直升機懸停控制

侯志寧1，顏富強2，鄧志雄3，王 婕4

（1. 天津航海儀器研究所，天津 300131；2. 92330部隊裝備部，青島 266100；3. 海南三亞市91458部隊，三亞 572021；4. 河北工業大學控制科學與工程學院，天津 300130）

考慮到小型無人直升機在飛行過程中存在的不確定對無人直升機飛行控制性能的影響，設計了一種基于滑模的非線性魯棒控制器。首先分析了懸停平衡條件下小型無人直升機的數學模型，然后通過設計滑模面，并結合標稱系統的反饋增益，獲得了滑模面的設計參數。在此基礎上設計了基于指數趨近律的滑模控制器，并利用Lyapunov理論對整個系統的穩定性進行了分析。最后的仿真結果表明：給出的滑模控制策略能夠有效地處理模型參數不確定對無人直升機飛行控制性能的影響，驗證了該控制策略的有效性。

無人機直升機；滑模；懸停；控制

小型無人直升機具有垂直起降、空中懸停、機動性好等特性，在軍民領域有著廣泛的應用前景，因此，成為當前無人機發展的一個重要方向[1]。然而，小型無人直升機是一個高度非線性、強耦合的復雜系統，其懸停控制是該領域研究的重點和難點問題。文獻[2-3]采用基于智能學習方法實現了無人直升機的懸停控制，取得了比較好的效果。文獻[4]給出了基于智能控制的無人直升機層級模型，并應用于R-50的無人機控制中。文獻[5]將遺傳算法和模糊控制相結合，實現了小型直升機的懸停控制。盡管，一些智能控制方法在無人直升機的懸停控制中得到了廣泛的應用，但是，也存在著一些問題，如智能控制方法對環境的自適應能力較差；神經網絡雖然能較好解決無人直升機系統中的一些非線性和模型攝動問題，但控制效果依賴于模型的精確程度[6-8]。

1 小型無人直升機數學模型

對小型無人機做如下假設：地球為慣性參考系，飛機為剛體，質量為常數且飛行過程中重力加速度為常值。將機體坐標作為參考坐標系，依據牛頓第二定律，可建立描述其小型無人機的運動方程。將獲得的方程在給定的平衡點處進行小擾動線性化，可獲得無人機小擾動線性化方程，如下所示：

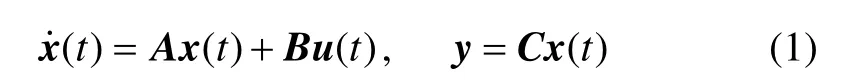
圖1 小型無人直升機參數示意圖Fig.1 Schematic of small unmanned helicopter parameters

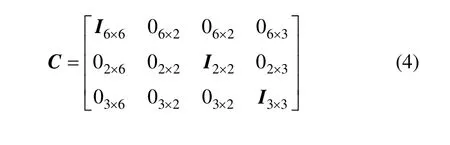
2 滑模控制器的設計

滑模控制是近年來發展較快的一種控制方法，滑模控制器的設計包括設計滑模面和到達條件。滑模面一般是根據性能指標的要求定義的，滑模面的定義要保證當系統滑動模態(一般為待控制狀態量)收斂到滑模面上時，系統的性能指標達到要求。所以滑模控制的任務是設計控制器使系統滑動模態最終收斂到滑模面上并且保持在滑模面上運動。

2.1 滑模面的設計

考慮模型參數匹配不確定對無人機模型的影響，將無人機的系統狀態方程(1)進一步寫為如下形式：

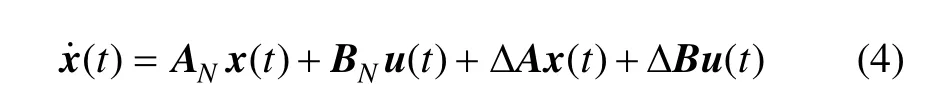
式中 ΔAx (t)和 ΔBu( t)分別是由于建模不準確引起的匹配不確定，即滿足條件：

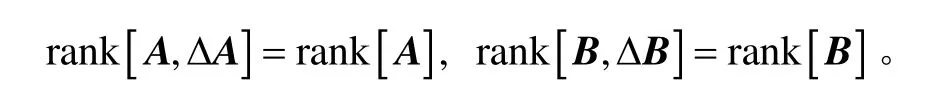
針對上述多輸入多輸出系統，設計滑模面：

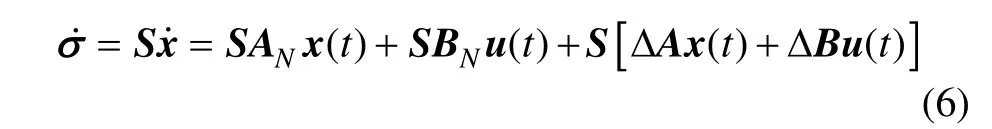
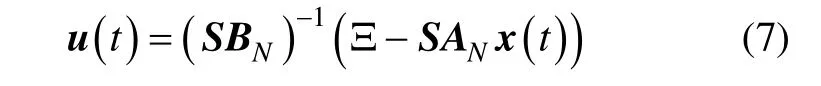
進一步可將控制律寫為如下的形式：

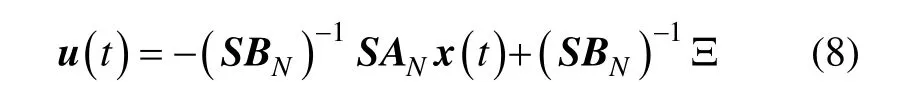
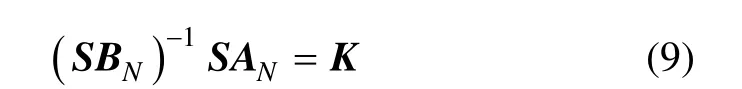
2.2 指數趨近律

根據滑模變結構原理，到達條件的設計必須保證滑動模態在有限時間內收斂到滑模面上并保持在滑模面上運動。目前研究較多的是符號函數到達條件，文獻[10]就是用的這種方法設計的滑模控制器。為消除抖振，這種方法還需定義一個邊界層，但邊界層的存在會降低系統的響應速度，并且導致穩態誤差的產生。針對符號函數到達條件的上述缺點，本文采用指數趨近律作為到達條件設計滑模控制器，有效解決了跟蹤速度慢和存在穩態誤差的問題，并且具有較強的魯棒性。

因此，為了獲得更好的動態性能，設計如下的指數趨近律：

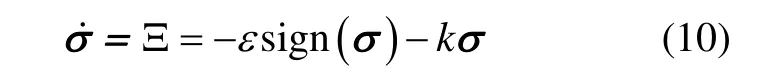
上述的指數趨近律的設計過程中，趨近速度從一個較大值逐步減小到零，不僅縮短了趨近時間，而且使系統運動軌跡到達切換面時的速度很小，能夠有效減弱控制抖振。

2.3 控制器及穩定性證明

根據上文滑模控制律可表示為如下形式：

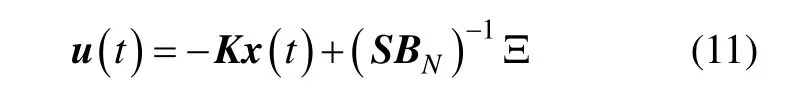
定理1：針對無人機縱向模型式(4)，選擇控制器為

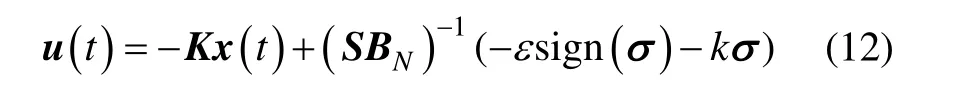
其中，sign(·)是符號函數，ε 、 k為可調參數，取式（5）形式的滑模面，則系統滿足滑模到達條件，且系統是漸近穩定的。

證明：選取Lyapunov函數：

對式(13)進行求導，可得：

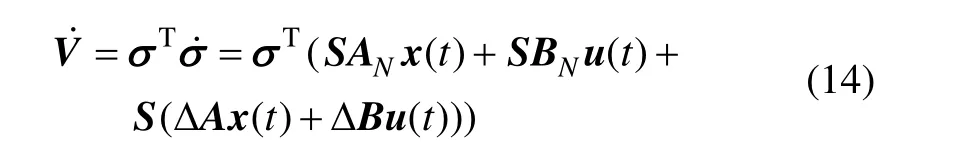
將式(10)和(11)帶入到(14)，可得到下式：

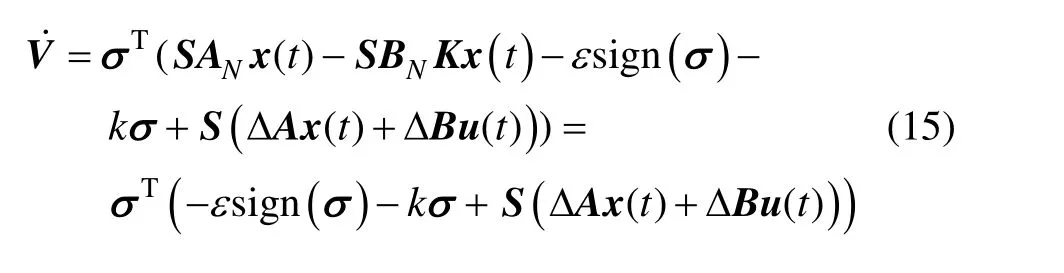
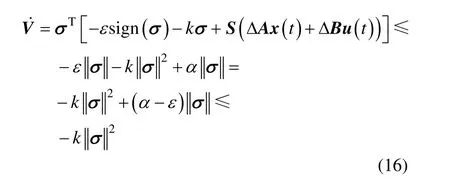
根據李亞普諾夫穩定性判據可得，本文給出的控制律將確保無人直升機系統最終穩定。

3 仿真驗證

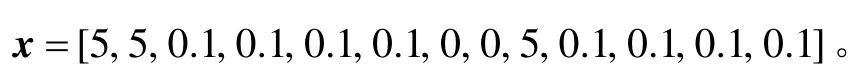
圖3 無人機懸停狀態下的控制變化曲線Fig.3 Control curves of UAVs in hover state

4 結 論

考慮模型參數不確定對控制性能的影響，提出了基于滑模的小型無人直升機懸停控制策略，并對滑模面和滑模控制器進行了設計，并利用Lyapunov理論證明了系統的穩定性，最后對加入不確定后的系統模型進行了仿真驗證。仿真結果表明該控制策略能夠有效處理模型參數不確定的影響，最終實現小型無人直升機的懸停控制。

（

）：

[1] Schmidt G T, Phillips R E. INS/GPS integration architecture performance comparisons[R]. Navigation Sensors and Integration Technology, RTO-EN-SET-064. London, UK: NATO, 2003: 127-132.

[2] Gao Guojiang, Lachapelle G. INS-assisted high sensitivity GPS receivers for degraded signal navigation[C]//ION GNSS. Texas, USA, 2006: 2977-2989.

[3] 王新龍，于潔. 基于矢量跟蹤的SINS/GPS深組合導航方法[J].中國慣性技術學報，2009，17(6)：710-717.

WANG Xin-long, YU Jie. Deeply SINS/GPS integrated navigation method based on vector tracking[J]. Journal of Chinese Inertial Technology, 2009, 17(6): 710-717.

[4] 張敏虎，任章，華春紅. UKF在深組合GPS/INS導航系統中的應用[J]. 中國慣性技術學報，2009，17(6)：697-700.

ZHANG Min-hu, REN Zhang, HUA Chun-hong. Application of UKF in deeply coupled GPS/INS navigation system[J]. Journal of Chinese Inertial Technology, 2009, 17(6): 697-700.

[5] Badu R, Wang Jinling. Ultra-tight GPS/INS/PL integration: A system concept and performance analysis [J]. GPS Solutions, 2009, 13(1): 75-82.

[6] Kim J W, Hwang D H, Lee S J. A deeply coupled GPS/INS integrated Kalman filter design using a linearized correlator output[C]// IEEE/ION, Position, Location, and Navigation Symposium. San Diego, California, 2006: 300-305.

[7] Dolecek G J, Mitra S K. On design of CIC decimation filter with improved response[C]//ISCCSP. Malta, 2008: 1072-1076.

[8] Badu R, Wang Jingling. Comparative study of interpolation techniques for ultra-tight integration of GPS/INS/PL sensors[J]. Journal of Global Positioning Systems, 2005, 4(1): 192-200.

[9] 唐康華. GPS/MIMU嵌入式組合導航關鍵技術研究[D]. 長沙：國防科技大學，2008.

TANG Kang-hua. Research on the key technology of embedded GPS/ MIMU integrated navigation[D]. Changsha: National University of Defense Technology, 2008.

[10] Ohlmeyer E J. Analysis of an ultratightly coupled GPS/INS system in jamming[C]//IEEE/ION, Position, Location, and Navigation Symposium. San Diego, California: 2006: 44-53.

Sliding mode control for small unmanned helicopter in hover

HOU Zhi-ning1, YAN Fu-qiang2, DENG Zhi-xiong3, WANG Jie4
(1. Tianjin Navigation Instruments Research Institute, Tianjin 300131, China; 2. Armament Department of Unit 92330, Qingdao 266100, China; 3. Unit 91458 of PLA, Sanya 572021, China; 4. School of Control Science and Engineering, Hebei University of Technology, Tianjin 300130, China)

In view that the uncertainty of the small unmanned helicopter in flight could influence its flight control performance, a nonlinear robust control strategy based on sliding mode control is proposed. At first, the mathematical model of the small unmanned helicopter is analyzed under equilibrium conditions in hover. Then a sliding mode surface is designed whose parameters are obtained from the feedback gain of the nominal system. The sliding mode control law is designed based on the index reaching law, and the whole system’s stability is analyzed by using Lyapunov theory. Simulation results show that the sliding mode control strategy can effectively deal with the parameter uncertainty’s influence on unmanned helicopter’s flight control performance, and verifies the effectiveness of the control strategy.

unmanned helicopter; sliding mode; hover; control

1005-6734(2014)05-0640-04

10.13695/j.cnki.12-1222/o3.2014.05.016

U666.1

A

2014-05-18；

2014-09-06

國家自然科學基金 （61203142）；河北省自然科學基金（F2014202206）；天津市自然科學基金（13JCQNJC03400）

侯志寧（1986—），男，工程師，從事慣性導航與控制研究。E-mail：zhnhou@163.com

聯 系 人：顏富強（1965—），男，高級工程師，從事慣性導航與控制研究。