靜電懸浮加速度計反饋引起閉環點漂移機理及抑制方法

劉 爽，劉云峰，董景新

（清華大學 精密儀器系 高精度導航技術教育部重點實驗室，北京 100084）

靜電懸浮加速度計反饋引起閉環點漂移機理及抑制方法

劉 爽，劉云峰，董景新

（清華大學 精密儀器系 高精度導航技術教育部重點實驗室，北京 100084）

靜電懸浮加速度計的檢測質量閉環點位置偏離電極框中心時會造成系統非線性誤差，調整檢測電路輸出電壓可調整檢測質量閉環點，而在調整過程中發現反饋電壓變化會引起電容檢測電路輸出電壓漂移，從而影響閉環點調節精度。為解決此問題，研究了閉環點位置與檢測電路輸出電壓變化的關系，推導了檢測電路傳遞函數，初步確定了反饋電壓對檢測電路輸出電壓影響的原因是隔直電容選取不恰當，通過實驗對比了材料為C0G、Y5P、X7R及SL的多層陶瓷電容作為隔直電容時輸出電壓與反饋電壓關系。實驗結果表明：采用低溫漂、耐高壓和受頻率影響小的C0G電容作為隔直電容能夠消除反饋對檢測電路引起的輸出電壓漂移，從而消除調節閉環點過程中閉環點位置的漂移，并且能提高檢測電路穩定性。

非線性；閉環點漂移；C0G電容；靜電懸浮加速度計

靜電懸浮加速度計工作原理與 MEMS電容式靜電加速度計工作原理類似，其閉環點位置對線性度具有重要影響[4]，只有當檢測質量閉環點位置位于電極框幾何中心位置時，外界加速度才與反饋電壓成線性。閉環點位置與檢測電路輸出電壓的零偏及零偏波動有關。檢測電路作用是將檢測質量偏離中心位置時產生的差動電容轉換成電壓量，通常采用差動變壓器式前端電路[5-6]。實際電路由于參數不對稱，檢測電路輸出電壓通常會存在一定的零偏值，使得檢測質量閉環點位置偏離幾何中心位置，從而造成系統非線性。因此需要調節檢測質量閉環點，采用變預載閉環點調節方法可將閉環點調節到電極框中心[7-8]。變化的預載電壓通過反饋通道經檢測電路作用在表頭。

在實驗中發現，當直流高壓作用在檢測電路反饋端時，檢測電路的開環輸出電壓會有幾毫伏到十幾毫伏漂移，相當于引起檢測電路零偏的變化，因此在進行閉環點位置調節時，變化的預載電壓（反饋電壓）必會引起檢測電路輸出電壓漂移，進而引起閉環點位置的漂移，帶來閉環工作點調節誤差。因此需要消除反饋電壓對檢測電路耦合作用。文獻[9]分析了 LISA中慣性傳感器前端電路反饋與檢測交叉耦合原因是電路濾波電容選取不恰當，文獻[10]報道了電容在高壓、頻率和溫度下容值改變的實驗現象。受其啟發，我們設計檢測電路也有可能是由于電容元件在高壓作用下性質改變造成輸出電壓漂移。因此針對我們自行設計的檢測電路，從理論上推導了反饋對檢測電路輸出耦合作用可能的原因，并通過實驗進行驗證，從而消除閉環點調節過程中閉環點漂移問題。

1 閉環工作原理及閉環點漂移來源

靜電懸浮加速度計工作原理如圖1所示：

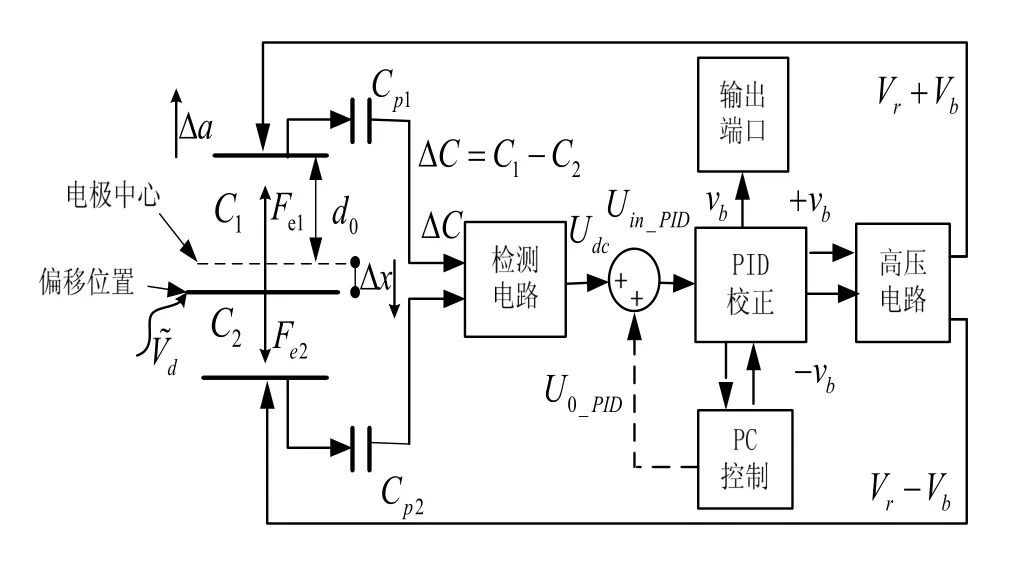
圖1 靜電懸浮加速度計工作原理圖Fig.1 Schematic of electrostatically suspended accelerometer

檢測電路輸出端有如下電壓關系：

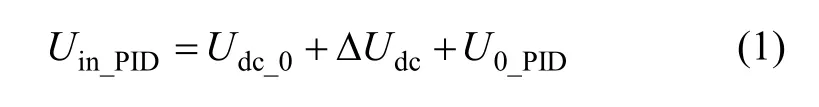
式中，Udc_0為檢測電路零偏，ΔUdc為差動電容引起檢測電路輸出電壓，二者構成檢測電路輸出電壓 Udc；U0_PID為閉環校正電壓；Uin_PID為PID輸入電壓。PID作用結果使得Uin_PID恒為零。

假設檢測電路無零偏（Udc_0=0），檢測質量閉環點位置位于電極框幾何中心（Δx0=0），且未加校正電壓（U0_PID=0）。當外界加速度引起質量塊位置偏移Δx時，與上下電極板產生差動電容 ΔC，則經過檢測電路轉化成差動電壓ΔUdc，經過PID控制電路和反饋高壓電路在上下極板產生±Vb反饋電壓。從而與預載電壓Vr一起生成靜電力Fe，拉動檢測質量塊回到初始位置，此時ΔC=0，因此ΔUdc=0。PID中積分器作用維持輸出 Vb1產生靜電力與外界力平衡。反饋電壓與外界加速度呈線性關系。

若Udc_0≠0，PID控制作用仍然是使得Uin_PID=0，最終結果是產生反饋電壓，生成靜電力拉動檢測質量塊運動，使得質量塊偏移中心位置位移為 Δx0，產生差動電容ΔC0，進而使得檢測電路產生差動變化電壓ΔUdc與Udc_0相抵消，以保證Uin_PID=0。顯然此時質量塊已經偏離幾何中心位置，即產生閉環點位置偏移，造成系統非線性。

ΔUdc與Δx關系推導如下：

式中，KΔC→Udc為檢測電路標度因數，C0為檢測值質量位于幾何中心；檢測質量與單側電極板形成電容值，即標稱電容。聯立式(2)(3)，并且注意到ΔUdc+Udc_0=0，可得檢測電路輸出電壓（零偏）與閉環點位置關系為：

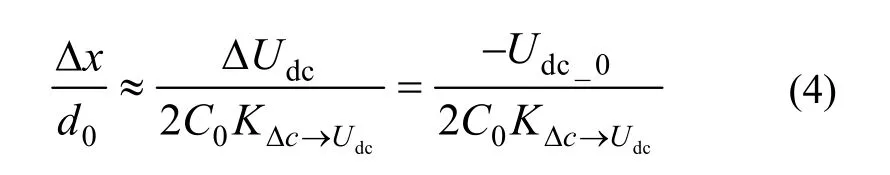
由于電路參數不對稱，檢測電路存在初始零偏，需要采用變預載閉環點調節方法對檢測質量閉環點位置進行調節[7-8]。其基本原理如下：通過變化預載前后預載和反饋電壓值，計算出閉環點偏移大小，從而計算出檢測質量位于幾何中心位置時的應有反饋電壓值；調整U0_PID=0大小，便可調整檢測質量在電極框中位置。檢測質量位于不同位置時得到的反饋電壓值不同，當實測的反饋電壓值與計算出的反饋電壓值相等時，檢測質量便調整到幾何中心位置。在調節閉環點時，發現變化的預載（反饋）電壓引起檢測電路開環輸出電壓漂移U′dc_0，進而引入額外的閉環點漂移 Δx′0，影響了閉環點調節精度。漂移大小可用式(4)計算。

在進行閉環點調節時，要求閉環點調節精度控制在 Δx/d0＜10-4，代入表 1中數據，可得為滿足上述要求時，X1、Y和Z2通道檢測電路輸出電壓漂移應分別小于0.64 mV、0.96 mV和0.48 mV。而實驗中發現檢測電路開環時，反饋端接入直流高壓時檢測電路輸出電壓漂移達到幾毫伏到十幾毫伏漂移，因此嚴重影響了閉環點調節精度，需要解決反饋電壓對檢測電路輸出電壓的耦合作用。

表1 X1、Y和Z2通道參數Tab.1 Parameters of X1, Y and Z2 channel

2 檢測電路模型分析

為找到反饋對檢測電路的耦合作用機理，需要從檢測電路傳遞函數入手。靜電懸浮加速度計檢測電路原理圖如圖2所示，C1、C2為表頭差動電容；表頭置于真空腔內，表頭電極和檢測電路通過屏蔽線相連，Cs1、Cs2為屏蔽線對地寄生電容；反饋電壓經電阻 Rb和濾波電容Cb分別加載到表頭兩端；Cp1、Cp2為高壓隔直電容，防止反饋高壓經過差動變壓器并耦合到輸出端，反饋電壓最高可達1 kV，因此Cp1、Cp2采用耐高壓多層陶瓷電容；L1、L2為差動變壓器初級，L3為次級；Cg、Cf與運放一起構成電荷放大器，選頻放大、乘法解調及低通濾波可等效為增益Kdc。

圖2 電容檢測電路原理圖Fig.2 Schematic of the capacitive detector circuit

2.1 等效電壓源分析

激勵電壓Um頻率采用240 kHz，反饋電阻Rb(100 k?)的阻抗遠大于Cp和Cs的交流阻抗。因此忽略反饋電阻對交流信號分流，僅考慮差動變壓器和電荷放大器組成的交流電路模型。

由基爾霍夫電流、電壓定律得：

根據變壓器耦合原理有：

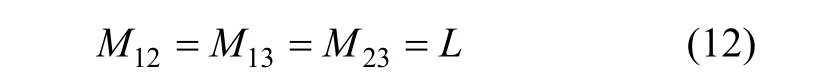
將式(9)～(12)聯立，有：

差動變壓器可等效為一帶內阻的電壓源，等效電路如圖3所示，UBR為差動變壓器等效電壓源，ZBR為等效阻抗。

圖3 等效檢測電路Fig.3 The equivalent of detector circuit

為求等效電壓源UBR大小，可將次級線圈開路，這時 UBR=Us，Is=0。聯立式(5)～(8)、(11)～(13)，并取Cs1=Cs2= Cs，Cp1=Cp2=Cp，ΔC=C1-C2得：

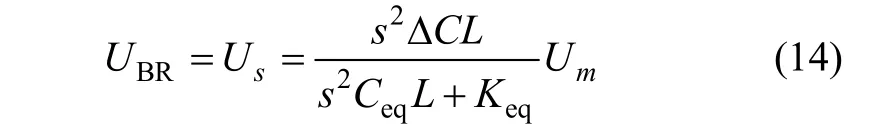
其中：

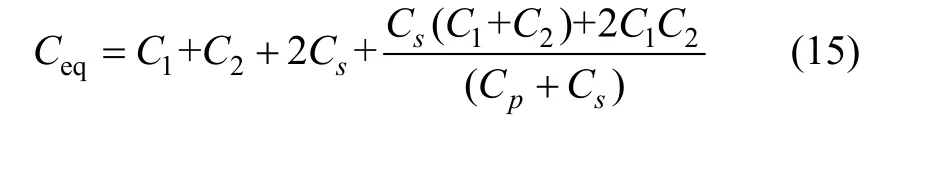
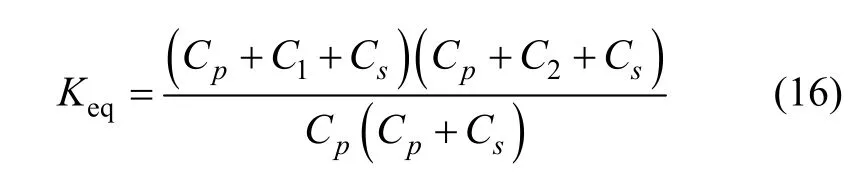
2.2 等效阻抗分析

如圖3所示，當Us短路時，Us=0，此時可根據開路電壓 UBR和短路電流 Is的比值計算變壓器等效阻抗，如式(17)所示：

當 Us= 0時，由式(13)可知：

聯立式(5)～(8)、式(11)和式(18)得：

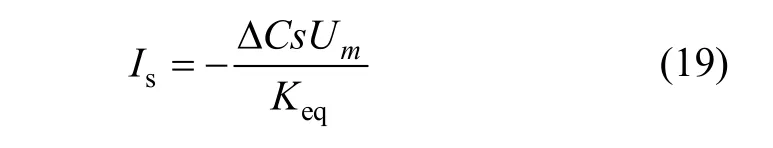
將式(14)和(19)代入(17)得：

2.3 反饋對檢測電路耦合影響機理分析

由圖2可推導檢測電路最終輸出電壓為：

將式(14)(20)代入式(21)，并令 s = jω得：

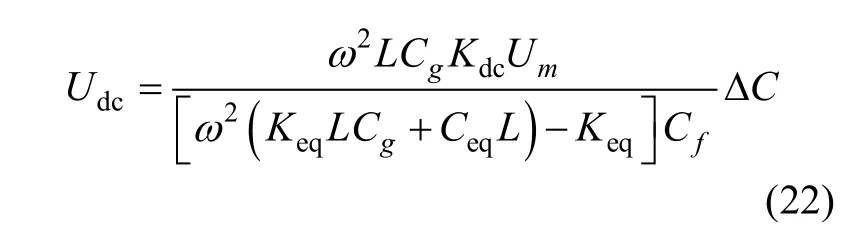
由Udc表達式可得如下結論：

● 在 Cs、Cp和 C0為定值時，Ceq、Keq為常數，其他參數也均為常數，此時檢測電路輸出電壓 Udc只與差動電容ΔC有關，且為線性關系。

● 在共振頻率 f0處，Udc達到最大值，共振頻率表達式為：

結合Ceq、Keq表達式可知：系統諧振頻率由表頭電容C1和C2、屏蔽線寄生電容Cs、隔直電容Cp、電荷放大器前端電容Cg、線圈電感L共同決定。任意一個變量改變均會引起系統諧振頻率變化，進而引起檢測電路傳遞函數和輸出電壓變化。

正常情況下，由于隔直高壓電容Cp1、Cp2作用，反饋直流高壓不會耦合到變壓器次級，少量的交流反饋電壓信號即使耦合到變壓器次級，也會經過后續選頻放大和乘法器解調和低通濾波大大衰減去除（乘法器解調頻率240 kHz）。因此，實驗中觀察到反饋對檢測電路耦合引起檢測電路輸出電壓漂移原因最可能是反饋高壓引起上述參數中某一參數改變，從而引起系統傳遞函數改變。

如圖2所示，反饋高壓作用在A、B兩點，電感線圈和電荷放大器電容Cg依靠隔直電容Cp與高壓隔離，因此可能改變參數的是反饋電壓直接作用的C1、C2、Cs和Cp。而C1、C2為表頭電容，Cs為屏蔽線對地分布電容，二者受高壓影響可能性很小，最大可能就是隔直電容Cp受反饋高壓作用電容值發生改變，從而影響 Udc。Cp采用的耐高壓的多層陶瓷電容，材料為Y5P，文獻[9-10]中報到過多層陶瓷電容在高壓下介電常數改變的情況，因此對于我們設計的電路有可能是隔直電容 Cp受高壓影響造成的檢測電路輸出電壓漂移，需要通過實驗進一步驗證上述推論。

3 實驗研究

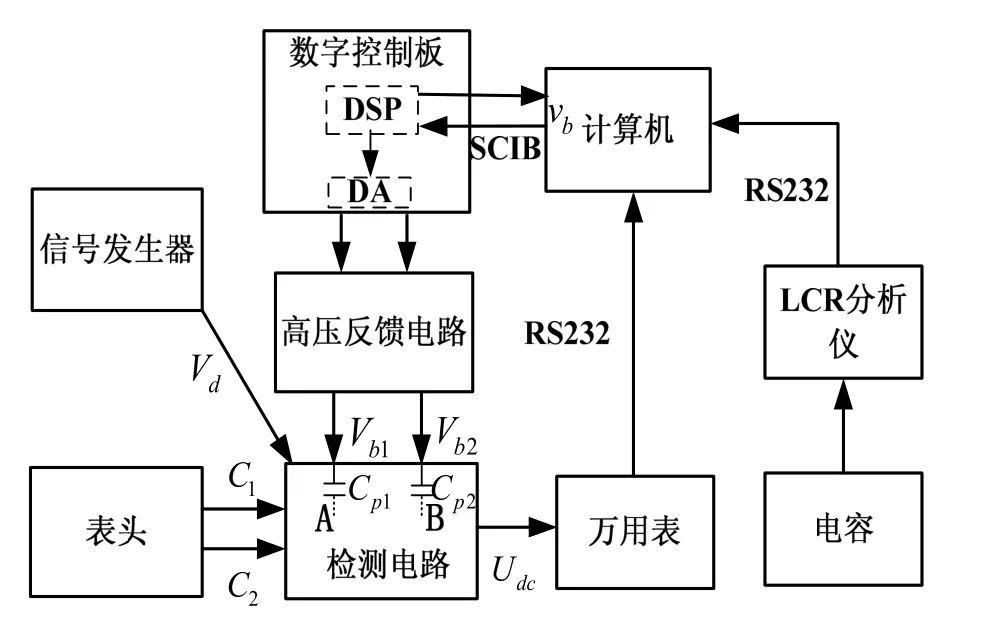
圖4 實驗裝置框示意圖Fig.4 Block diagram of experiment

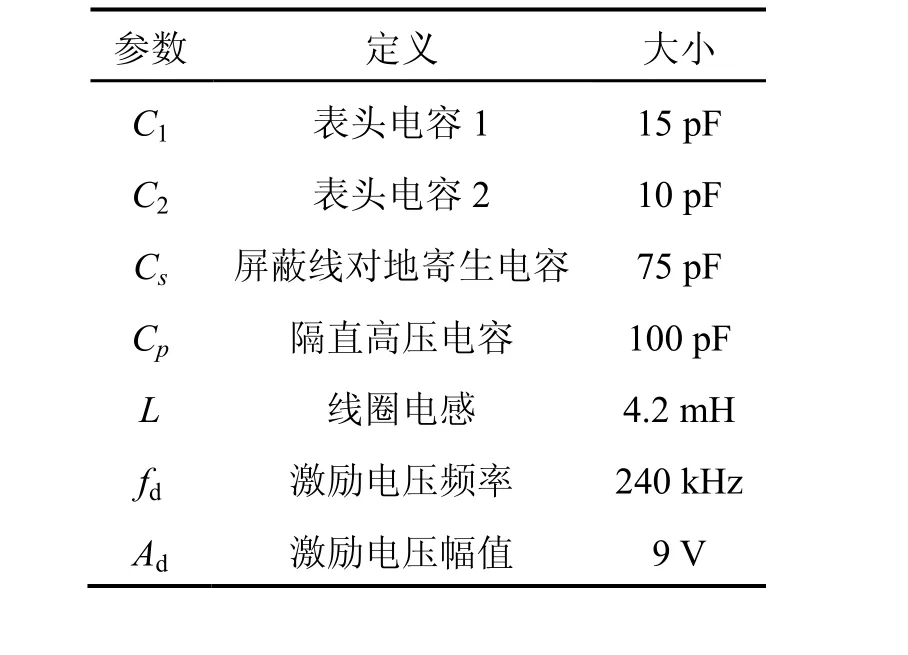
表2 實驗中檢測電路參數Tab.2 Parameters of detector electronics circuit

采用不同Cp電容做對比實驗。實驗裝置示意圖如圖4所示，電路參數如表2所示，采用標稱電容同為100 pF的不同材料的多層陶瓷電容（見表3）替換Cp1和Cp2。之前電路的Cp采用的是Y5P（Y5P2）電容，發現具有耦合現象。C0G電容被證實具有低溫漂、耐高壓等特點，容值幾乎不隨外界影響而發生改變[9-10]，可作對比試驗。所采用電容均為耐高壓電容。

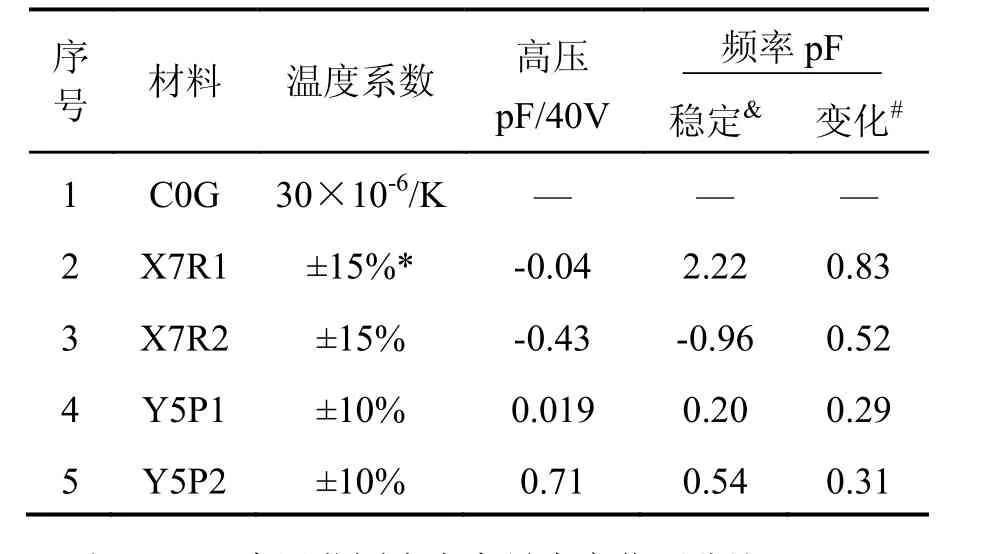
表3 不同型號電容參數Tab.3 Parameters of different capacitors

Cp1和Cp2采用Y5P（Y5P2）或C0G電容在高壓下實驗結果如圖5所示。可見當大小為40 V的反饋電壓單獨作用在Cp1或Cp2時，均會使得檢測電路輸出電壓Udc發生跳變，幅度最大變化20 mV左右，且改變趨勢相反，與反饋電壓正負極性無關，且 Udc跳變量隨著時間衰減；當反饋電壓同時作用在Cp1和Cp2時，對檢測電路產生的影響可以抵消一部分，但由于電容差異不能完全抵消，Udc仍然存在5 mV左右的跳變。上述現象說明了反饋電壓對檢測電路耦合作用引起檢測電路輸出電壓漂移，從而影響系統閉環點位置。

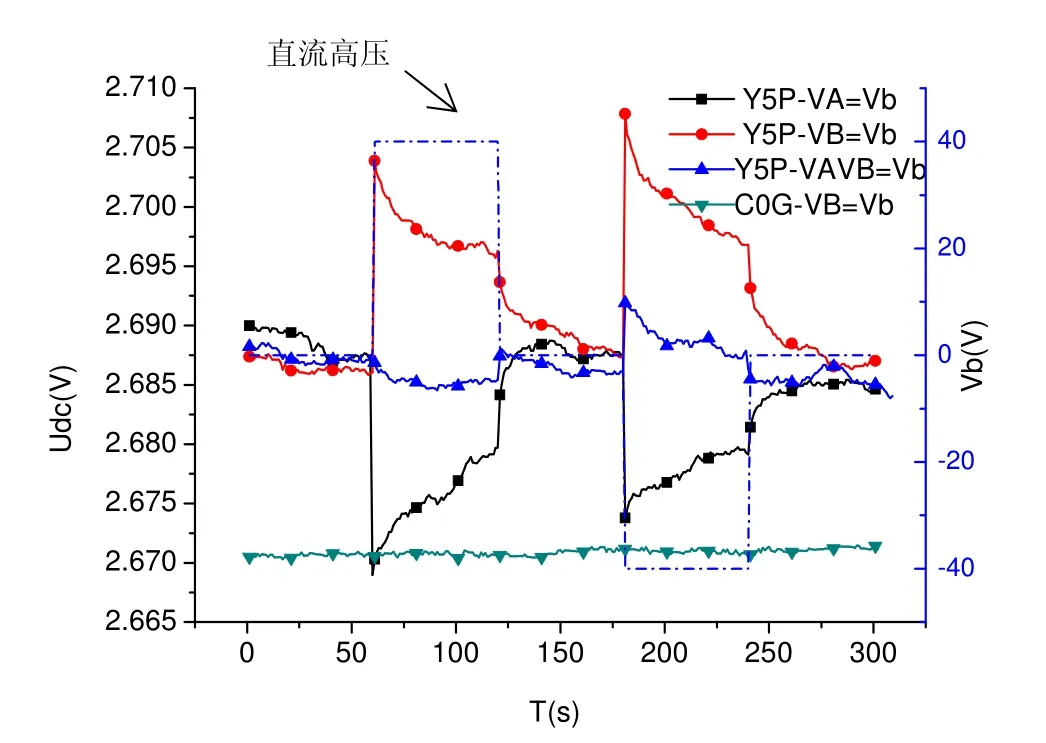
圖5 采用Y5P或C0G電容時Udc與Vb關系Fig.5 The Udc for Y5P or C0G under Vb

當Cp1和Cp2采用C0G電容時，Udc沒有明顯變化。

以上實驗結果證實了反饋對檢測電路耦合作用是由于Cp在高壓作用下容值改變造成的，與之前理論分析相符。采用C0G電容時，在進行變預載閉環點調節時，不會引起閉環點位置漂移，解決了變預載過程中閉環點漂移問題。

圖6所示Cp2采用不同容值C0G，得到Udc與Cp2線性關系，可見當 Cp2增加時，檢測電路輸出電壓增加，因此可以根據檢測電路輸出電壓變化，判斷 Cp2電容增大或減小，通過線性擬合得到ΔCp2與ΔUdc的比例系數KC-U=0.03869 V/pF，進而可求出Cp2在反饋高壓作用下改變量。

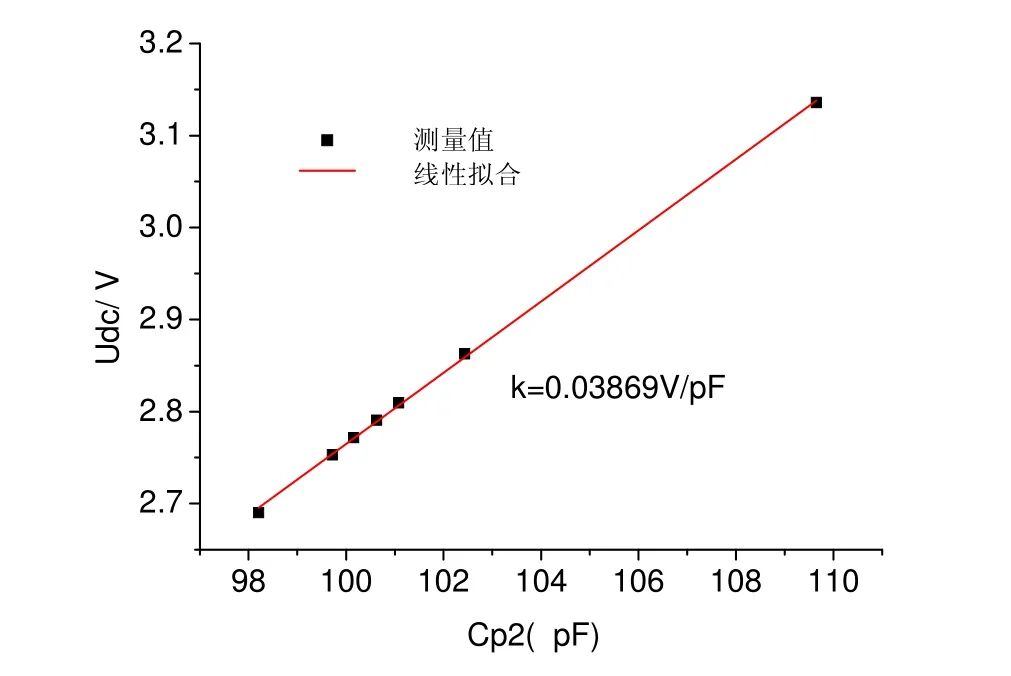
圖6 Udc與Cp2關系Fig.6 The relationship between Udc and Cp2

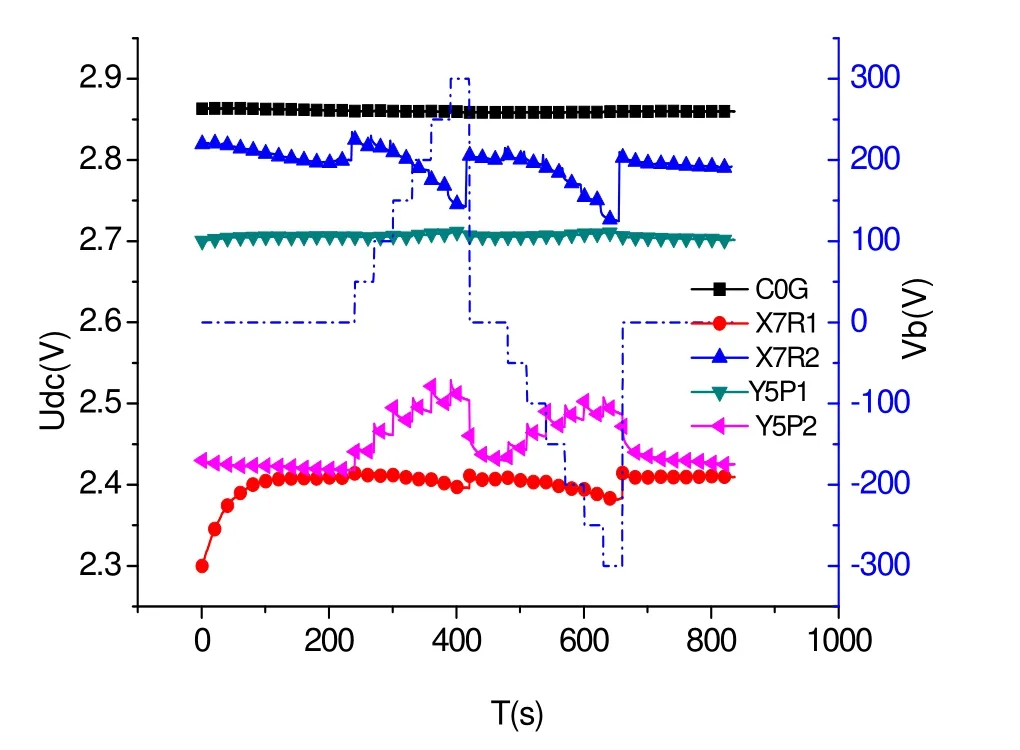
圖7 不同電容在不同電壓下Udc值Fig.7 The Udc under different Vb with different Cp

Cp1采用C0G電容，Cp2采用不同材料電容，得到不同Vb作用下Udc結果如圖7所示。可見電壓在0～300 V范圍變化時，C0G電容大小幾乎不變；其他幾種電容均受高壓影響，且影響大小不一致，且 Udc并不為常數，而是隨時間衰減，說明上述電容值受高壓影響存在非線性關系。根據KC-U和ΔUdc可以求出每40 V高壓作用下電容改變量大小，結果如表3所示。

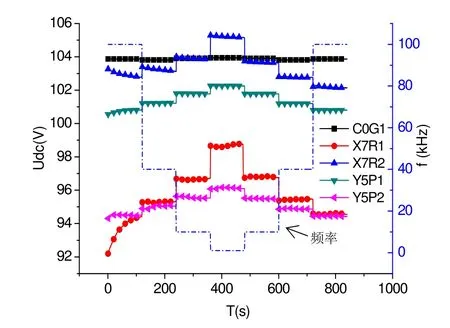
圖8 不同頻率下電容值Fig.8 Capacitances under different frequencies

由圖7和表3中電容受高壓影響實驗結果可知，同種材料的多層陶瓷電容由于廠家不同，受高壓改變量也不一致。

為研究電容與頻率關系，利用LCR分析儀在幅值1 V、不同頻率下測量電容隨頻率變化關系，實驗結果如圖8。由圖8可見，除C0G外，其他幾種電容均隨頻率變化。圖5和圖7曲線開始階段的漂移也是由于電容剛接入電路時受頻率影響容值改變而造成檢測電路輸出電壓漂移，因此頻率變化也會引起電容容值變化，從而對檢測電路輸出產生影響，引起閉環點位置漂移。電容受頻率影響具體數值見表3。

此外多層陶瓷電容還受溫度影響，從而引起檢測電路輸出電壓漂移，溫度影響情況同樣匯總于表3[10]。

本文開始提到，在進行靜電懸浮加速度計閉環點調節時，閉環點調節精度在10-4量級，X1、Y和Z2通道電路輸出電壓漂移應分別小于0.64 mV、0.96 mV和0.48 mV，再根據KC-U可得Cp變化應分別小于0.017 pF、0.025 pF和0.012 pF。

因此綜合考慮高壓、溫度和頻率的影響，上述電容中只有C0G電容滿足要求。因此將Cp電容材料由原來的Y5P替換為C0G解決了變預載過程中閉環點位置漂移問題，有助于實現閉環點精確調節，此外還能夠提高檢測電路穩定性，降低噪聲。

4 結 論

本文通過理論和實驗研究確定了反饋電壓造成檢測電路輸出電壓漂移的原因是檢測電路隔直電容選取不恰當。采用C0G電容替代原有Y5P電容，消除了反饋電路對檢測電路間耦合作用，從而解決了變預載閉環點調節過程中閉環點位置漂移的問題。同種材料、不同廠家的多層陶瓷電容受高壓、頻率和溫度影響不一致，C0G電容受上述因素影響最小，因此選用此電容有助于提高檢測電路整體性能。

（

）：

[1] Danzmann K. LISA—an ESA cornerstone mission for the detection and observation of gravitational waves[J]. Advances in Space Research, 2003, 32(7): 1233-1242.

[2] Hudson D, Chhun R, Touboul P. Development of a differential accelerometer to test the equivalence principle in the microscope mission[J]. Acta Astronautica, 2005, 57(2): 341-347.

[3] Touboul P, Foulon B, Christophe B, et al. CHAMP, GRACE, GOCE instruments and beyond[J]. Geodesy for Planet Earth, 2012, 136: 215-221.

[4] Wan Caixin, Dong Jingxin, Liu Yunfeng, et al. Nonlinearity of a closed-loop microaccelerometer[C]//2007 IEEE International Conference on Control Applications. Singapore, 2007: 1260-1265.

[5] Josselin V, Touboul P, Kielbasa R. Capacitive detection scheme for space accelerometers applications[J]. Sensors and Actuators A: Physical, 1999, 78(2): 92-98.

[6] Bai Yanzheng, Zhou Zebing, Tu Haibo, et al. Capacitive position measurement for high-precision space inertial sensor[J]. Frontiers of Physics in China, 2009, 4(2): 205-208.

[7] Fan Da, Liu Yunfeng, Han Fengtian, et al. Identification and adjustment of the position and attitude for the electrostatic accelerometer's proof mass[J]. Sensors and Actuators A: Physical, 2012, 187: 190-193.

[8] 范達. 星載靜電懸浮加速度計的設計與地面實驗研究[D]. 北京：清華大學，2013.

FAN Da. Design and ground experimental study of a spaceborne electrostatic levitated accelerometer[D]. Beijing: Tsinghua University, 2013.

[9] Gan L, Mance D, Zweifel P. Actuation to sensing crosstalk investigation in the inertial sensor front-end electronics of the laser interferometer space antenna pathfinder satellite[J]. Sensors and Actuators A: Physical, 2011, 167(2): 574-580.

[10] Prymak J, Randall M, Blais P, et al. Why that 47 μF capacitor drops to 37 μF, 30 μF, or lower[C]//Proc. of the CARTS USA Conference. March 2008.

Mechanism and suppression method for feedback-caused close-loop position fluctuation of electrostatically suspended accelerometer

LIU Shuang, LIU Yun-feng, DONG Jing-xin
(Key Laboratory for High-precision Navigation Technology of Ministry of Education, Department of Precision Instrument, Tsinghua University, Beijing 100084, China)

The nonlinearity of electrostatically suspended accelerometer (ESA) is related to the closed-loop position of proof mass (Pm), which can be adjusted by changing the output of detection circuit (Udc). It is found that Udccan be changed by feedback voltage (Vb) during the adjustment, thus causing the fluctuation of Pm. In order to solve this problem, the relationship between Pmand Udcis studied, and the transform function of detection circuit is deduced. The contrast test is carried out with C0G, Y5P, X7R and SL capacitances under different Vband frequencies. Theoretical and experimental results show that the reason for the fluctuation of Udccaused by Vbis the variation of the isolation capacitance caused by Vb. Using the C0G capacitance, which is immune to temperature and high voltage and frequency, not only could overcome the fluctuation of Pmduring adjustment, but also improve the stability of the detector circuit.

nonlinearity; closed-loop position fluctuation; C0G capacitance; electrostatically suspended accelerometer

1005-6734(2014)05-0682-06

10.13695/j.cnki.12-1222/o3.2014.05.024

U666.1

A

2014-06-06；

2014-09-19

清華大學自主科研計劃（20091081243）

劉爽（1985—），男，博士研究生，從事微重力關鍵技術研究。E-mail：s-liu08@mails.tsinghua.edu.cn

聯 系 人：董景新（1948—），男，教授，博士生導師。E-mail：dongjx@mail.tsinghua.edu.cn