云重心方法在艦炮維修性評價中的應用

劉勇，徐廷學，孫臣良

(1.海軍航空工程學院接改裝訓練大隊，山東煙臺264001;2.海軍航空工程學院兵器科學與技術系，山東煙臺264001)

艦炮是重要的艦載武器，為使其具有良好的維修性，需要進行維修性評價。目前多采用定量評分法，很強硬地讓專家給出一個分值，忽略了維修性描述及評價的不確定性，易造成評價信息的丟失。在進行系統性能評價的過程中，不可避免地要考慮模糊性和隨機性。二者聯系緊密，難以分開［1-2］。與模糊綜合評判法、集值統計法、層次分析法、主分量法等系統性能評價方法相比，云理論的優勢是它在定性定量的轉換過程中綜合考慮了模糊性和隨機性的關聯性，使轉換結果更加科學。云重心方法已廣泛應用于各種復雜系統的綜合評價。但是，已有的研究成果尚存在以下不足:1)當將定性評語轉化為云模型時，基于3倍熵規則的熵參數的確定方法不夠合理，且缺乏有效的確定超熵參數方法，使評價云發生器的設置不合理，影響到評價的準確性;2)利用歸一化運算求解單個定量指標的云重心位置與理想云重心位置的離差存在偏差，且求解綜合云重心偏離度的算法較為繁瑣。針對這些問題，對云重心方法進行改進，并應用于艦炮維修性評價。

1 云理論概述

定義1 設U是一個用精確數值表示的定量論域，C是U上的定性概念，若定量值x∈U是C的一次隨機實現，x對C的確定度μ(x)∈［0，1］是有穩定傾向的隨機數 μ:U→［0，1］?x∈Ux→μ(x)則 x在論域U上的分布稱為云，每個x稱為一個云滴［3］。

云用期望值Ex、熵En、超熵He3個數值來整體表征一個概念，把模糊性和隨機性很好地融合到一起，為定性與定量的結合提供了數學依據。

定義2 設U是一個用精確數值表示的定量論域，C是U上的定性概念，若定量值x∈U是C的一次隨機實現，x滿足 x～N(Ex，En'2)，其中 En'～N(En，He2)，且x對 C的確定度滿足 μ=exp［-(x-Ex)2/(2En'2)］，則x在U上的分布稱為正態云。

云模型中，定性概念與定量數據之間的相互轉換是通過云發生器來完成的。其中正向正態云發生器根據云的數字特征 Ex、En和 He產生云滴drop(xi，μi)，其具體算法見文獻［4-5］。

2 評語的云模型表示

2.1 評語的云化過程

評語的云化是將各個評語用正態云的3個特性(E x，En，He)來表示，生成評價云。云模型和區間數之間有良好的映射關系，且云化的關鍵在于合理度量專家對該評語的定性認識。因此，應由各專家給出概念對應的區間數，然后對區間數進行集結［6］，最后轉換為云模型。

1)專家給出各個評語對應的區間數。設專家集為 E={Ei}(i=1，2，…，t)，評語集為 S={sj}(j=1，2，…，m)，專家 Ei在論域[0，1]上給出 sj的區間數記為 cij=［aij，bij］，0≤aij＜bij≤1，則專家群體的評判矩陣為 C=(cij)t×m。

2)將C=(cij)t×m按列進行集結并平均，獲得云化區間數cj為

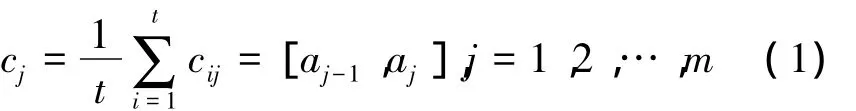
3)運用云模型與區間數的轉換關系，將各云化區間數轉化為云模型。評語集與云化區間數cj的對應關系為 sj～ cj=［aj-1，aj］。當 j=1，m 時，cj對應的定性評語用半云模型來描述;當j=2，3，…，m-1時，cj對應的定性評語用對稱云模型來描述。

設一個對稱云模型對應的區間數為［a，b］，文獻［7］采用指標近似法確定其特征參數如下:

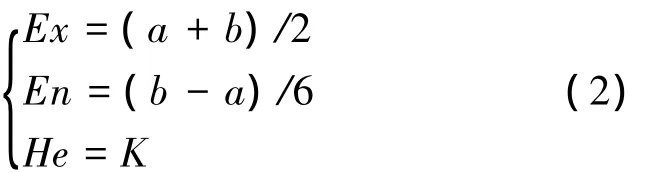
2.2 2倍熵規則的提出及熵的改進模型

式(2)確定熵的方法顯然是基于3En規則［1，8］，即認為區間長度是熵的 6倍，區間［Ex-3En，Ex+3En］之外的云滴可以不考慮。因此，評價云發生器的各個云圖不會有交叉。圖1很好地證明了這一點，圖中按照式(2)確定各云對象的期望與熵。

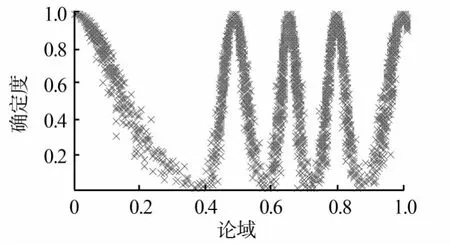
圖1 區間長度為6倍熵時評價的云發生器Fig.1 Evaluation cloud generator with the interval length of 6 times of the entropy

既然云模型是表達定性概念的，那么每個云滴至少應對一個概念具有確定度，但從圖1可看出，存在μ(x)≈0的點。對某個具體的云模型來說，根據3En規則，當x=Ex±3En時，就應該有μ(x)=0。

事實上，各云圖之間在確定度較弱的區域呈現出交織狀態。因為在連續的論域空間上，肯定存在這樣一些云滴，它們對程度上相鄰的2個概念M和N的確定度μM(x)與μN(x)差別很小甚至相同，因此很難清晰地分辨出云滴確定的是M還是N。這種交織體現出了概念在對程度表達上的模糊性與連續性。問題的關鍵是如何確定μM(x)≈μN(x)處的云滴x。為此，先對確定度的強弱進行劃分。

定義3 對于描述定性概念M的云模型，若x∈［Ex-En，Ex+En］，稱x對定性概念M 有強確定度;若 x∈［Ex-En，Ex-2En)∪［Ex+En，Ex+2En)，稱x對定性概念M有中等確定度;若x∈［Ex-2En，Ex-3En)∪［Ex+2En，Ex+3En)，稱 x對定性概念M有弱確定度。

劃分的依據是:在x=Ex±En處，μ(x)≈0.61;在x=Ex±2En處，μ(x)≈0.15;在 x=Ex±3En處，μ(x)≈0。

在 x∈［Ex-2En，Ex-3En)∪［Ex+2En，Ex+3En)上，μ(x)比較小，且 μ(x)在 x=Ex±2En 處取得最大值，因此，可以認為在x=Ex±2En處，云滴對相鄰2個概念M與N的確定度都較小，且最難區分出云滴屬于哪個概念的云對象。于是，把x=Ex±2En 2個相鄰云模型的交織點，并讓完整云對應的區間數的長度d=4En，即認為表達定性概念的云滴主要落在［Ex-2En，Ex+2En］內。這是本文提出的2倍熵(2En)規則。這樣界定是合適的，因為位于區間［Ex-2En，Ex+2En］上的云滴對一個定性概念的貢獻占總貢獻的95.44%。

于是，當 j=2，3，…，m-1時，期望與熵的確定方法如下

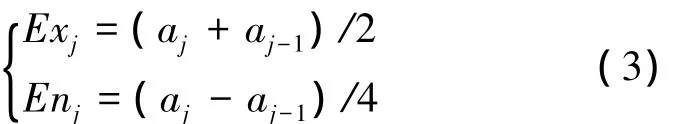
c1對應的云模型為半降云，cm對應的云模型為半升云，期望與熵的確定方法為

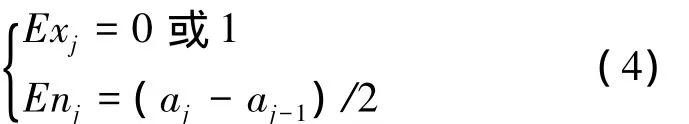
式中:a0=0，am=1，半降云的期望值取0，半升云的期望值取1。只需要由式(4)確定的對稱云模型的一半，即圖像位于對稱軸左邊(cm對應的云模型)或右邊(c1對應的云模型)的那部分。

2.3 基于差異度的超熵確定模型

所有云滴構成的隨機變量X的分布被稱為泛正態分布，超熵 He是 X偏離正態分布的度量［9］。文獻［8，10］展示了超熵對云圖的影響。文獻［11］指出，當He＜En/3時，云X的泛正態狀態較為明顯，當He＞En/3時，云滴呈現為霧化狀態，因此，將He=En/3稱為云的霧化點。文獻［6］認為:當He＜En/3時，不確定度較小;當He＞En/3時，不確定度較大。

文獻［7］認為式(2)中的K值可根據評語的不確定性和隨機性確定，但并未闡述具體的確定方法。文獻［6］認為，專家對某一定性概念認知的不確定度是表達該定性概念的區間數長度d的增函數。該文獻還指出:當d小于某一界限值dk時，可認為專家對定性概念認知的不確定度較小，He應小于En/3，此時取He=0.1En;當d＞dk時，可認為專家對定性概念認知的不確定度較大，此時取He=0.3En;dk一般取論域［0，τ］的長度的1/10。

上述文獻涉及的熵是由式(2)確定的，按照文獻［11］的觀點，當由式(3)確定 En時，取 He=0.2En為霧化點。

文獻［6］確定超熵的方法存在的2點不足:1)區間數的長度大并不意味著專家對定性概念認知的不確定度也大，區間長度在論域上的劃分是受評價慣例影響的。比如一般認為得分低于總分的60%為不及格，而不是50%。對于本文案例，當論域為［0，1］時，0.6左側領域只能算是“差”，而不能算是“中”。這樣帶來的結果是，評語“劣”與“差”對應的區間數的總長度為0.6，而另外3個評語對應的區間數的長度之和為0.4。2)給出dk的取值時未考慮評語的數目。本文案例中評語個數為5，區間數的平均長度為0.2，且其區間數的長度均超過了論域長度的1/10，按照該文獻的模型，He必然取值偏大。

審視將定性概念映射為區間數，再將區間數轉換為云模型的過程，不難發現:對于云圖中的某一個特定的x，μ(x)的離散程度很大程度上受專家對區間數劃分意見的影響。因此，可認為專家對某一區間數的界定的差異越大，云的超熵越大。下面給出衡量專家給出的區間數與云化區間數之間的差異度η的模型。

定義4 對于第j個評語sj，設專家Ek(k=1，2，…，t)給出的區間數為，計算求得的云化區間數為 cj=［aj-1，aj］，令 dj=aj-aj-1，則差異度 ηj的計算方法為

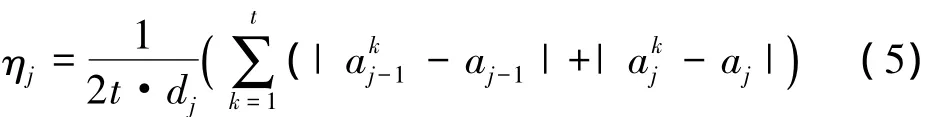
式中:j=1，2，…，m。

下面分2種情況進行討論:

1)將雙邊約束的區間數(即 j=2，3，…，m-1)轉化為對應的云模型時超熵的取值。當ηj≤0.15時，可認為各專家對區間數cj的界定的差異較小，云的泛正態化較為明顯;只要ηj未達到ηu=0.2，就可以認為專家對區間數cj的界定的差異不算很大，云不應呈現出較明顯的霧化狀態。基于這樣的考慮，建立超熵的計算模型如下:

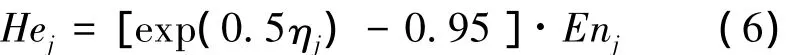
式中:j=2，3，…，m-1。

2)將單邊約束的區間數(j=1，m)轉化為云模型時超熵的取值。對于半云模型，當ηj≤0.075時，可認為各專家對區間數cj界定的差異較小，云的泛正態化較為明顯;只要ηj未達到ηu=0.1，就可以認為專家對區間數cj界定的差異不算很大，云應不應呈現出較明顯的霧化狀態。于是可建立超熵的計算模型為

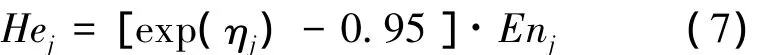
式中:j=1，m。

建立的超熵計算模型具有以下性質:

1)He是η的增函數;

2)當 η=0 時，He=0.05En＞0，仍能保證云的泛正態狀態;

3)當η=ηu時，He接近但未達到0.2En，云不會呈現較明顯的霧化狀態。

3 評價意見的集結

3.1 單項指標值的云集結

通過各專家評判，各指標都將產生t個評價意見，其中有用數值表示的定量指標，也有用語言值來描述的定性指標。t個評價意見的集結值用一個云模型表示。設某個指標的t個評價意見的云對象的期望為(Ex1，Ex2，…，Ext)(定量指標的Exi為其第i個數值)，該項指標集結值云模型的期望為Ex，則定量指標Ex集結方法為［12］

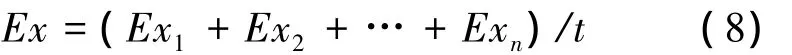
定性指標的Ex集結算法如下

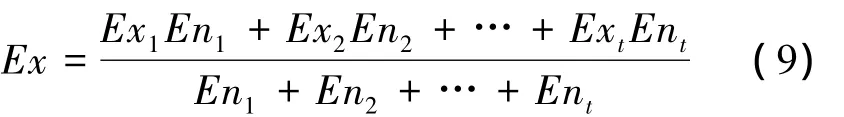
3.2 綜合云重心偏離度的計算

n個評價指標值可用n個云模型來表示，系統狀態就可用1個n維綜合云來表示。云重心偏離度θ用來衡量n維綜合云重心與理想狀態下n維綜合云重心的差異。令T=(T1，T2，…，Tn)為綜合評價云的云重心向量，L=(Ex1，Ex2，…，Exn)為云重心位置向量，H=(h1，h2，…，hn)為云重心高度向量，則［12-13］

式中:Ti=Exi×hi，(i=1，2，…，n)。文獻［12］認為 H為各指標的權重向量，即 H=(ω1，ω2，…，ωn)。

文獻［12-13］求綜合云重心偏離度的方法如下:設在理想狀態下，n維綜合評價云重心位置向量為L0=(E，E，…，E)，則在此狀態下綜合云的重心向量為對綜合云重心向量進行歸一化運算，得到向量TN=(，…，)，計算方法為

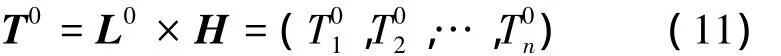
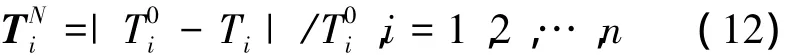
把TN乘以權重值，然后再相加，有

下面指出這種算法的不足并進行改進。

首先，式(12)每一項都有ωi，把它約去，此式可簡化為

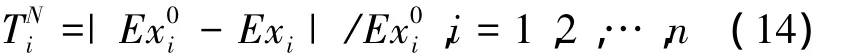
其次，通過歸一化運算求解單個定量指標的云重心位置與理想云重心位置的離差不合理，現舉例說明。若一個定量指標的理想狀態值為8，其各個狀態值或專家提供的評價數值按式(8)集結后為12，則按式(14)計算的重心位置離差為0.5。如果采用本案例的五級評語，按照行業標準，12為“良”，但是，對于本文案例，當指標的重心位置偏離理想重心位置1為0.5時，意味著“差”。為此，將定量指標的集結值映射到定性評語對應的區間數中。

定義5 設 I1=［l1，u1］和 I2=［l2，u2］是定義在正實數域上的2個區間數，I1為對象GA的值域的一個子集，I2為對象GB的值域的一個子集，dI1=u1-l1＞0為 l1到 u1的距離測度，dI2=u2-l2＞0為 l2到u2的距離測度，定義I1到I2的一一映射為ξ:I1→I2，對應法則ξ表示等比轉換，對任意的x∈I1，x'∈I2，x'為 x 的象，滿足

不妨設一個定量指標Gr為成本型指標，即狀態值越小越好。于是對于該指標的一個狀態值fv，應存在 0＜f1＜f2＜…＜fm-1，使得能夠界定定量評價標準并建立定量標準與定性評語的對應關系如下

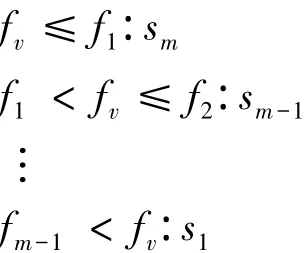
設該指標的各個值進行集結后的期望為Exag，該值對應的定性評語為sj，下面分3種情況進行討論Exag轉換為定性評語時的云重心位置。

1)當 j=2，3，…，m-1 時，sj對應的定量評價標準界定的區間為(fm-j，fm-j+1］，由式(15)，Exag經等比轉換后在定性評語對應區間數中的位置為

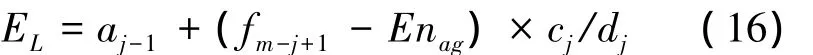
2)當j=1時，設該指標的最大狀態值為Vmax，由式(15)，Exag經等比轉換后的云重心位置為

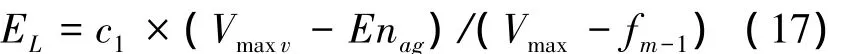
3)當j=m時，定量評價標準界定的區間其實為［0，f1］，于是由式(15)，Exag經等比轉換后的云重心位置為

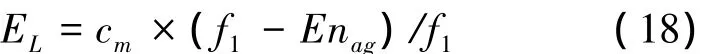
照此方法，同樣可建立Gr為效益型指標時的轉換模型。這樣，在求偏離度時，全部按定性指標處理，且可把式(13)進一步簡化為

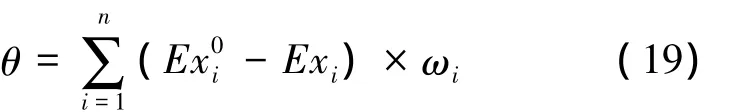
3.3 評價結果的確定

根據評語集、區間數與云模型之間的對應關系，在各個區間數上用相應的云模型表示出相應的評語，就構成了一個評價云發生器。

將求得的偏離度θ輸入到定性評價云發生器中，通過激活的云對象來確定評價結論。偏離度θ的意義在于將多維云的云重心位置組成的云重心向量集結成一個點xa，且有xa=E-θ。給定閾值δ∈［0.1，0.2］，考察各評語云對象的 μi(xa)(i=1，2，…，5)。設確定度最大的為maxμi(xa)，與之相鄰的云對象在xa處的確定度為μj(xa)，那么:

1)當 maxμi(xa)-μj(xa)＞δ時，第 i個評語值即可作為對艦炮維修性定性評價的結果輸出;

2)當 maxμi(xa)-μj(xa)≤δ時，xa為評價結果的定量輸出，而其定性表述可由專家另外給出。

4 案例分析

艦炮初樣機試驗階段，管理部門邀請了10名專家，對其機械系統進行維修性評價。

4.1 將評語轉化為云模型

規定評語集為

S={sj|j=1，2，…，5}={劣，差，中，良，優}

10名專家給出各評語對應的區間數之后，按式(1)計算出各評語對應的云化區間數，如表1所示。

進一步計算各云化區間數的長度，然后由式(5)計算專家意見與云化區間數的差異度為

η1=0.026 3，η2=0.101 0，η3=0.152 9，η4=0.128 9，η5=0.068 3.

再由式(3)、(4)、(6)、(7)計算各評語的云化模型參數，如表2所示。

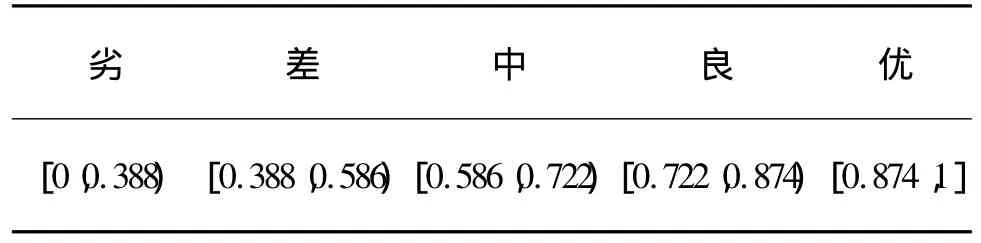
表1 各評語對應的區間數Table 1 Intervals of remark terms

表2 各評語對應的云模型參數Table 2 C loud model parameters of rem ark term s

4.2 計算綜合云重心偏離度

維修性評價指標及權重如表3所示。G1為定量指標，其余指標為定性指標。

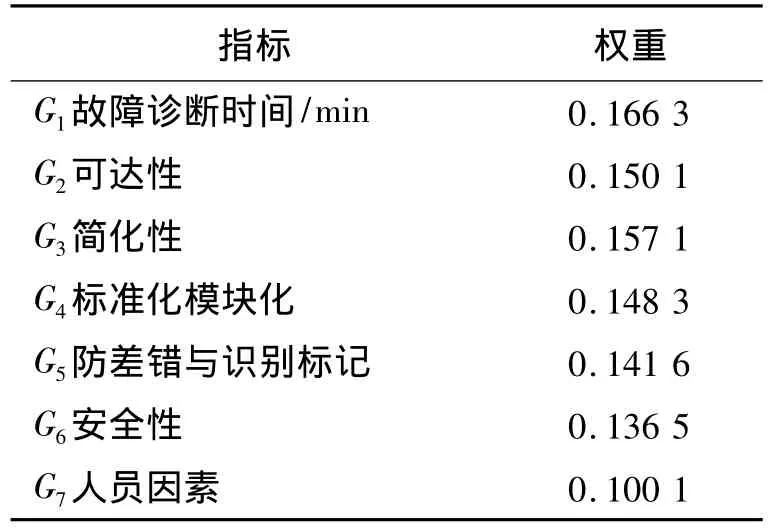
表3 評價指標及其權重Table 3 Evaluation indexes and their weights

檢測診斷時間Rt與評價等級的對應關系如表4所示。

表4 診斷時間評價標準Table 4 Evaluation standard of diagnosis tim e

專家的評價意見如表5所示，其中故障診斷時間是由專家估計得到的。將表5中專家群體對單項指標的意見運用式(8)或式(9)進行云集結，期望值如表6所示。

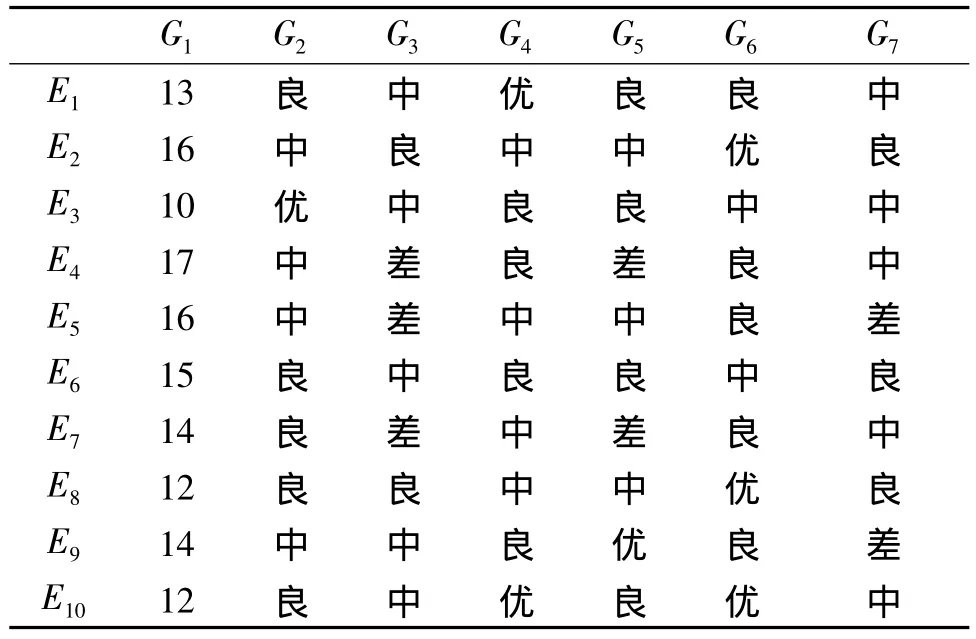
表5 專家的評價意見Tab le 5 Expert evaluation views

表6 各指標綜合云的期望Table 6 Expected value of index

將ExG1=13.9按式(16)進行等比轉換，得到其云重心位置為ExG1＇=0.725 8。然后利用式(19)計算評價結果的云重心偏離度θ=0.259 6。

4.3 確定評價結果

由表2中各評語對應的云模型參數構成的評價云發生器如圖2所示。取δ=0.1，將θ的值輸入到評價云發生器，xa將激活“良”和“中”2個云對象，對“良”的確定度約為0.33，對“中”的確定度約為0.05，由于0.33-0.05＞δ，于是可判定該裝備維修性水平為良。若按式(9)計算TN1=0.39，那么對指標G1的綜合評價應為“中”，但按定量評分標準，對其評價屬于“良”，這樣就有了偏差。接下來再按式(10)計算偏離度 θ'=0.278 9，xb=0.721 1，也激活“良”與“中”2個云對象，且xb對“中”的確定度約為0.15，對“良”的確定度約為0.13，0.15-0.13＜δ。于是判定該艦炮維修性水平介于中和良之間，傾向于中。云重心xa與xb如圖3所示，y1指示的圓點表示xa對“中”的確定度，y2表示xb對“良”的確定度。由此可看出，以往的偏離度求解模型是存在明顯的誤差的。

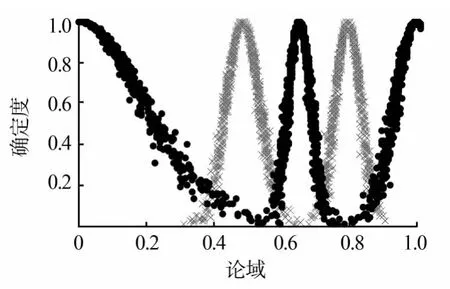
圖2 2倍熵規則下的定性評價云發生器Fig.2 Evaluation cloud generator with two-entropy rule

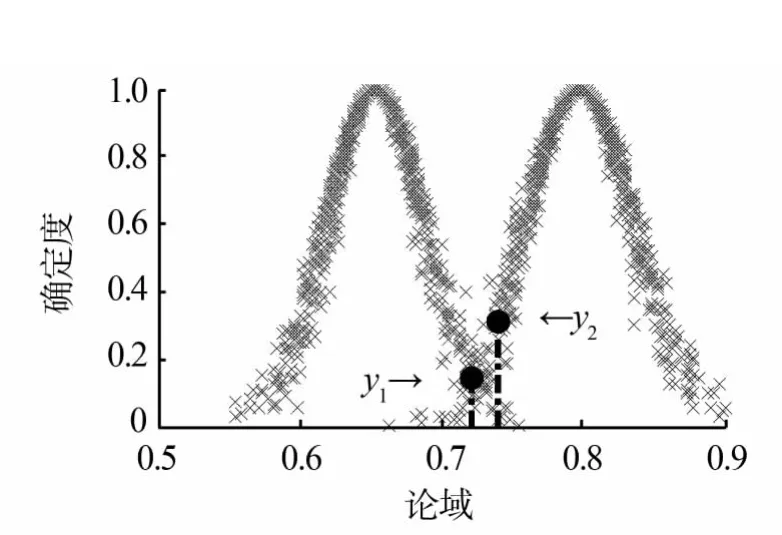
圖3 評價結果Fig.3 Evaluation result

根據文獻［6］的方法確定各評語云的超熵，則評價云發生器中各云模型的超熵均為其熵的0.3倍。它顯然放大了專家對同一個問題認識的差異程度。在這樣趨于霧化的發生器中進行評價時，難以直觀判斷出偏離度對所激活的云對象的確定度。

5 結束語

對云重心評價方法進行了改進，并應用于艦炮的維修性評價。在評價實例中，把根據改進模型與已有模型建立的評價云發生器進行對比，可看出根據改進模型設置云發生器的參數是合理的，而已有模型與云理論的基本原理不相符。通過將改進的綜合云重心偏離度求解模型與原有模型的評價結果進行對比分析，可看出改進算法是簡便且準確的，用于艦炮維修性評價是可行的。本文考慮的定量指標是成本型的，若是效益型指標，同樣可建立等比轉換關系，改進綜合云重心偏離度的求解算法。

［1］GOU Jin.N-D normalmembership cloud model based on region partition［J］.Journal of S of tware，2010，5(3):288-295.

［2］WANG Shouxin，ZHANG Li，MA Na，et al.An evaluation approach of subjective trust based on cloud model［J］.Journal of S of tware Engineering＆ Applications，2008，1:44-52.

［3］TAO Limin，HUANG Decai，HONG Libin.Research on subjective srustmodel based on cloud model for open networks［J］.Journal of Computational Information Systems，2011，7(13):4844-4854.

［4］FU Qian，CAIZhihua.Decision tree based on cloud model and its application in slope stability prediction ［J］.Journal of Information＆ Computational Science，2010，11(7):2240-2247.

［5］LIU Yuchao，MA Yutao，ZHANG Haisu，et al.A method for trust management in cloud computing:data coloring by cloud watermarking［J］.International Journal of Automation and Computing，2011，8(3):280-285.

［6］岳勇，楊宏偉，白勇，等.一種基于云模型和懲罰函數的多屬性評價方法［J］.裝甲兵工程學院學報，2012，26(1):92-97.YUE Yong，YANG Hongwei，BAIYong，et al.A method of multiple attributive evaluation based on cloud model and castigation function［J］.Journal of Academy of Armored Force Engineering，2012，26(1):92-97.

［7］SHIYanbin，ZHANGAn，GAOXianjun，et al.Cloudmodel and its application in effectiveness evaluation［C］//The15th International Conference on Management Science＆Engineering September.Long Beach，USA，2008:250-255.

［8］WANG Zhaohong.Application of cloud theory in association rules［J］.I.J.Information Technology and Computer Science，2011(3):36-42.

［9］LIU Lizhen，WANG Wentao，ZHANG Maohong.The quality assessment of student learning based on cloudmodel［J］.Journal of S of tware，2012，7(3):588-593.

［10］WANG Zhaohong.Cloud theory and fractal application in virtual plants［J］.I.J.Intelligent Systems and Applications，2011(2):17-23.

［11］劉禹，李德毅，張光衛，等.云模型霧化特性及在進化算法中的應用［J］.電子學報，2009，37(8):1651-1658.LIU Yu，LIDeyi，ZHANG Guangwei，et al.Atomized feature in cloud based evolutionary algorithm［J］.ACTA Electronica Sinica，2009，37(8):1651-1658.

［12］廖良才，范林軍，王鵬.一種基于云理論的組織績效評估方法［J］.系統工程，2010，28(1):99-104.LIAO Liangcai，FAN Linjun，WANG Peng.Method of evaluating organizational performance based on cloud theory［J］.Systems Engineering，2010，28(1):99-104.

［13］張目，周宗放.改進的云重心評判法在高技術企業信用評價中的應用［J］.數學的實踐與認識，2010，40(19):37-43.ZHANG Mu，ZHOU Zongfang.An improved MCGC and its application in credit evaluation of high-tech enterprises［J］.Mathematics in Practice and Theory，2010，40(19):37-43.