柴油機缸內輻射換熱三維數值模擬

付麗榮，張文平，明平劍，羅躍生

(1.哈爾濱工程大學動力與能源工程學院，黑龍江哈爾濱150001;2.哈爾濱工程大學理學院，黑龍江哈爾濱150001)

高負荷柴油機的輻射傳熱占總傳熱量的10%～45%［1］，直接關系到發動機熱效率以及因傳熱引起的各種熱負荷、熱強度問題;同時，輻射熱流量對燃燒性能的影響很大，因此需對缸內輻射傳熱進行深入研究［2-3］。柴油機缸內輻射傳熱的研究主要基于實驗［4-6］和數值模擬［7-9］;實驗研究法，即用熱輻射傳感器直接測量氣缸內輻射傳熱量或者用二色法測量氣缸內火焰溫度，再求得輻射傳熱量。數值模擬主要利用商用軟件，如 Fluent［8］、AVL-Fire［9］。目前主要的輻射傳熱模擬方法有:區域法、蒙特卡洛法、離散傳遞法、有限體積法、無網格法［10］等。而有限體積法，可確保輻射能量整體守恒，對不規則邊界適應性強，易處理各向異性散射，可以采用與流場計算相同的網格，在迭代計算中可以不對溫度和熱流進行插值計算。因此本文采用有限體積法進行編程，從而可以與通用流體力學數值模擬軟件(general transportation equation analysis，GTEA)［11］的流場計算采用同一套網格，簡化了計算程序，提高了計算的通用性。

本文在前期工作基礎上，針對三維輻射傳熱進行數值模擬。本文借助有限體積法計算三維封閉空腔內的輻射傳熱，并用3個算例——六面體、圓柱體和TBD620型柴油機的ω燃燒室來驗證此方法和程序的可靠性與準確性，同時考慮了網格離散個數和立體角離散個數對計算結果的影響。

1 控制方程

1.1 輻射傳熱方程

對于吸收、發射、散射性灰介質的輻射傳遞方程表達式如下［12］

式中:κ、σs分別為吸收系數和散射系數，β0=κ+σs為衰減系數;I為空間位置r、方向s處的輻射強度;Ib為黑體輻射強度，Ib=6T4/π;σ為斯蒂芬-玻爾茲曼常數，為 5.67×10-8W/(M2·K4)Φ(s，si)為輻射從入射方向s到散射方向si的散射相函數;Ωi是中心方向為si的立體角。

本文所研究的介質是非散射的，所以方程(1)可以簡化為

1.2 輻射傳熱方程的邊界條件

RTE的邊界條件定義如下

式中:εw為壁面發射率，下標w表示壁面位置，nw為單位法向量。式(3)表示當輻射能離開一個光學反射面時有2部分的貢獻，一是高溫表面放出的輻射量，二是投射到此表面的反射量。

2 數值離散

2.1 有限體積法

為了得到離散化方程，將方程(2)對控制體ΔV和立體角ΔΩmn積分，可得ΔΩmn內輻射能量守恒方程的有限體積表達式:

應用Gauss定理把體積分轉換成面積分，假設輻射強度I和Ib在控制體和立體角內為常數，同時，源項在之內為均勻的，則方程(4)的左端和右端分別可以表示為如下形式:

將式(5)、(6)代入到方程(4)，可得

式中:

將空間區域離散為互不重疊的四面體或三棱柱單元，所有變量信息存儲在單元中心，如圖1(a)的點1、2、3、4所示。將4π角域離散為互不重疊的控制立體角 ( Nθ×Nφ)，把方向矢量smn定義為立體角的中心方向，θ是0～π變化的極角，φ是0～2π變化的方位角，如圖1(b)所示。控制角被平分成Δθm=θm+-θm-= π/Nθ，Δφn= φn+-φn-=2π/Nφ。當立體角是確定時，方向權的符號決定了控制體表面的輻射能是流進還是流出，它由下式表示:

本文采用一階迎風格式將單元界面上的輻射強度與單元中心的輻射強度關聯起來，則它們的關系表示如下

式中:

將式(13)代入式(7)，則式(7)可寫成如下線性方程組:

式中:

圖1 混合網格和立體角示意圖Fig.1 Diagram of hybrid grids and the solid angle

2.2 邊界條件離散

邊界條件可以離散成如下形式

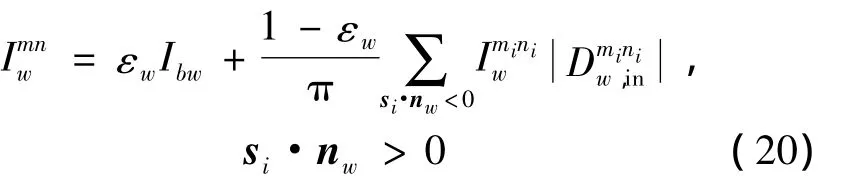
式中:

2.3 壁面輻射熱流密度

壁面輻射熱流密度表示為

3 數值計算結果及分析

本文的輻射換熱數值模擬是應用GTEA軟件，在文獻［13］基礎上，為了驗證本文的UFVM方法，并且在三維輻射問題上檢驗所開發的計算程序的可靠性，本文選擇2個基本的幾何體，即六面體、圓柱體。

3.1 不規則六面體輻射模擬

驗證算例1是對不規則六面體區域內的輻射進行仿真并與文獻中結果進行對比。幾何體結構的建立和參數的設定與文獻［12］中的數據一致。如圖2(a)所示，其中z0=1 m，所有邊界為黑體面，溫度為0，壁面發射率為εw=1，內部介質溫度為100 K。空間離散為六面體單元，見圖 2(b)，(Nx×Ny×Nz)= (27×27×27)，立體角劃分為( Nθ×Nφ)= ( 8×16)，吸收系數分別采用10、1和0.1 m-1進行計算，不考慮散射，計算底面的無量綱熱流量分布。本文將計算結果(如圖3所示)與精確解和數值解［12］進行對比，可以看到本文的計算結果與精確解吻合很好。

圖2 六面體模型與網格Fig.2 A hexahedral enclosure and mesh

由圖3可見，當吸收系數是10 m-1時，無量綱熱流在底面中心處的值接近于1.0，主要是由于底面此時只受到周圍介質的影響;在兩邊處熱流迅速減小，因為此時兩邊受到邊界冷壁面的影響。當吸收系數為0.1 m-1時，熱流急劇下降，這是因為介質被冷邊界冷卻的結果。

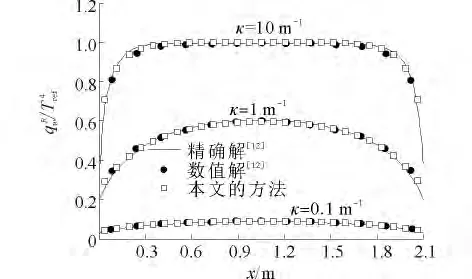
圖3 底面上AB線段無量綱熱流比較Fig.3 Comparison of radiative wall heat flux along line AB on the bottom wall of a quadrilateral enclosure

圖4 網格的影響Fig.4 The effect of different discrete grids

圖5 網格和立體角劃分均不同時的誤差Fig.5 The error of different both grids and solid angles

圖4給出了吸收系數為1 m-1時，立體角離散個數均為 ( Nθ×Nφ)= ( 4×8)，空間區域分別離散為19 683個單元和12 167個單元時計算結果與精確解的相對誤差分布。由圖可知網格加密后的相對誤差不但沒有明顯的變小，反而在某些位置還有所變大。當空間離散為12 167個單元，立體角離散個數為 ( Nθ×Nφ)= ( 4×8)時，與單元個數為 19 683，立體角離散個數為 ( Nθ×Nφ)= ( 8×16)時，計算結果與精確解的相對誤差分析見圖5。由圖可看出當網格加密且立體角離散個數增多時，計算誤差明顯減小，計算結果更接近于精確解。因此，在數值計算中，空間離散的網格并不是越密越好，而是要和立體角離散的個數相對應，即如果空間網格離散的個數增加，那么相應的立體角離散的個數也要增加，才可以得到更高精度的數值解。

3.2 圓柱體輻射模擬

驗證算例2是半徑為1m，z軸方向長度為2m的圓柱體。邊界為黑體，溫度為0，壁面發射率為εw=1，內部氣體溫度為100 K，圓柱體和空間網格見圖6。在吸收系數分別為0.1，1.0和5.0m-1情況下，計算圓柱體右側邊界的無量綱輻射熱流量，空間域離散為74 203個四面體單元，立體角劃分為 ( Nθ×Nφ)= ( 8×16)。本文的計算結果與文獻［14］提供的精確解和文獻［15-16］的數值解進行對比，結果如圖7所示，可以看出它與精確解和數值解吻合很好。

圖6 圓柱體和網格Fig.6 The cylinder enclosure and mesh

圖7 無量綱輻射熱流量的對比Fig.7 Comparison of dimensionless radiative heat flux along the lateral side of the cylinder

圖7顯示了在3種吸收系數0.1、1.0和5.0 m-1下右側邊界的無量綱輻射熱流量，當吸收系數是5.0 m-1時，到達右側壁面中間處的輻射熱流密度接近于介質的黑體輻射強度，這是由于壁面的輻射強度只受封閉壁面周圍的熱氣體的發射本領影響。然而，在兩邊角處，輻射熱流迅速減小，因為受周圍頂部和底部冷壁面影響。但當吸收系數是0.1 m-1時，介質的輻射本領是弱的，并且無量綱輻射熱流量大幅度下降，這是因為受其他冷壁面和光學薄氣體可忽略的自身衰減的深遠影響。

4 ω型燃燒室輻射模擬

驗證算例3是TBD620型柴油機ω型燃燒室。發動機的基本參數:氣缸數為16，沖程為195 mm，缸徑為170 mm，連桿長度為350 mm，壓縮比為13.5。在燃燒結束至排氣開始前這一階段，此時活塞在下止點位置，缸蓋、缸壁和活塞溫度均為350 K，假設氣體平均溫度為800 K;利用GAMBIT軟件劃分網格，通過軟件將網格文件轉換為CGNS格式，并讀入本文開發的求解器;空間域內采用混合網格，氣缸內為三棱柱非結構化網格，ω型燃燒室內采用四面體網格，網格總數為63 227，圖8(a)、(b)分別顯示了計算網格的主視和俯視圖;立體角劃分為( Nθ×Nφ)= ( 8×16)。計算燃燒室縱向中心截面邊界線左側、下側和右側的輻射熱流密度，圖9中s為0～200、200～432.7、432.7～632.7mm 區間分別代表邊界線左側、下側和右側。

圖8 計算網格Fig.8 Computational grid

圖9 s的定義Fig.9 Definition of s

圖10顯示的是工質吸收系數對缸內縱向中心截面的左側、下側和右側邊界無量綱輻射熱流密度的影響。從432.7～632.7 mm區間可以看出3種吸收系數的熱流量圖都是對稱的，與算例2的圓柱體模型結果圖7對比可知，算例3的底面的ω型燃燒室與算例2底面是圓形的效果一樣，所得的側面熱流量圖都是對稱的，即底面的形狀對側邊的輻射熱流量沒有影響。在0和200 mm周圍，由于兩邊角處受頂部和底部冷壁面影響，所以熱流量值變小。當吸收系數為0.1 m-1時，工質相當于是透明的，所以各位置的熱流量幾乎一樣大。

圖10 不同吸收系數下的無量綱輻射熱流量的對比Fig.10 Comparison of dimension less radiative heat flux of different absorption coefficients

圖11顯示的是吸收系數為10.0 m-1時，工質溫度分別為600、800、1 000 K時缸壁無量綱輻射熱流量。介質溫度對中心部位的熱流量影響較大，對邊角處的影響較小;邊角處由于受冷壁面的影響，熱流量值變小。

圖11 介質不同溫度下的無量綱輻射熱流量的對比Fig.11 Comparison of dimensionless radiative heat flux of medium of different temperatures

5 結論

本文通過六面體、圓柱體及ω型燃燒室的數值模擬，得出如下結論:

1)本文方法的數值解與精確解和文獻中的數值解吻合較好，可見，本文的非結構有限體積法和求解器GTEA適用于三維輻射換熱的數值模擬。

2)不同的網格劃分和立體角劃分對計算結果有相應的影響，空間離散的網格并不是越密越好，而是要和立體角離散的個數相對應，即空間網格離散的個數要與立體角離散的個數同時增加，空間離散產生的假散射與角度離散產生的射線效應在一定程度上才會互相抵消，所以可以得到更高精度的數值解。

3)可將程序應用于柴油機燃燒室的輻射換熱模擬，燃燒室缸壁的輻射熱流量會受到缸內工質的吸收系數和溫度的影響;無量綱輻射熱流密度隨著工質吸收系數的增大而增大，工質溫度對中心部位的熱流量影響較大，對邊角處的影響較小。為后續考慮碳黑顆粒的輻射傳熱對柴油機工作性能的影響打下了基礎。

［1］沈季勝，沈瑜銘，陳紅巖，等.柴油機氣缸內傳熱模型研究歷程與展望［J］.內燃機工程，1999，20(1):72-77.SHEN Jisheng，SHEN Yuming，CHEN Hongyan，et al.Prospect and research process on radiated heat transfer models in cylinder of diesel engine［J］.Chinese Internal Combustion Engine Engineering，1999，20(1):72-77.

［2］嚴兆大，沈季勝，劉震濤，等.用蒙特卡洛法計算柴油機缸內多元熱輻射［J］.內燃機學報，2000，18(2):133-136.YAN Zhaoda，SHEN Jisheng，LIU Zhentao，et al.Calculation of the radiation heat transfer in cylinder of diesel engine by the Monte-Carlo method［J］.Transactions of CSICE，2000，18(2):133-136.

［3］熊仕濤，陳國華.柴油機缸內傳熱計算［J］.內燃機學報，2001，19(3):215-218.XIONG Shitao，CHEN Guohua.Calculation of in-cylinder heat transfer of diesel engine［J］.Transactions of CSICE，2001，19(3):215-218.

［4］潘克煜，周龍保，楊中樂.直噴式柴油機氣缸內輻射傳熱的試驗研究［J］.內燃機工程，1996，17(4):59-67.PAN Keyu，ZHOU Longbao，YANG Zhonglu.Experimental investigation of in-cylinder heat radiation in diesel engine［J］.Chinese Internal Combustion Engine Engineering，1996，17(4):59-67.

［5］SAID A M，BUTTSWORTH D R，YUSAF T F.A review of radiation heat transfer measurement for diesel engines using the two-colour method［C］//Proceeding of 3rd International Conference on Energy and Environment.Malaysia，2009:202-207.

［6］高天，潘克煜，陳飛.直噴式柴油機缸內氣體輻射傳熱的研究［J］.西安交通大學學報，2006，40(3):302-306.GAO Tian，PAN Keyu，Chen Fei.Investigation on in-cylinder radiation from gases in DI diesel engine［J］.Journal of Xi＇an Jiaotong University，2006，40(3):302-306.

［7］宋有生，聶宇宏.燃燒室型線對缸內燃燒和輻射傳熱影響的計算分析［J］.科學技術與工程，2008，8(3):760-763.SONG Yousheng，NIE Yuhong.Calculation investigation on influence of combustion chamber pr of ile to combustion process and radiative heat transfer［J］.Science Technology and Engineering，2008，8(3):760-763.

［8］姜曉光，聶宇宏，謝凱弘，等.基于Fluent的柴油機缸內輻射換熱分析［J］.科學技術與工程，2008，8(15):4099-4103.JIANG Xiaoguang，NIE Yuhong，XIE Kaihong，et al.Diesel engine cylinder internal radiation heat transfer analysis based on Fluent［J］.Science Technology and Engineering，2008，8(15):4099-4103.

［9］劉健，呂繼組，計時鳴.柴油機缸內輻射換熱的多維數值模擬研究［J］.機械工程學報，2009，45(12):311-317.LIU Jian，LYU Jizu，JIShiming.Study onmulti-dimensional numerical simulation of in-cylinder radiation heat transfer of diesel engine［J］.Journal of Mechanical Engineering，2009，45(12):311-317.

［10］SADAT H，WANG C A，DEZ V L.Meshless method for solving coupled radiative and conductive heat transfer in complexmulti-dimensional geometries［J］.Applied Mathematics and Computation，2012，218:10211-10225.

［11］明平劍.基于非結構化網格氣液兩相流數值方法及并行計算研究與軟件開發［D］.哈爾濱:哈爾濱工程大學，2008:16-72.MING Pingjian.Development of numerical modeling for gas-liquid two-phase flows based on unstructured grids and parallell computing［D］.Harbin:Harbin Engineering University，2008:16-72.

［12］BEAk SW，KIM M Y，KIM JS.Nonorthogonal finite-volume solutions of radiative heat transfer in a three-dimensional enclosure［J］.Numer Heat Transfer B，1998，34:419-437.

［13］MING Pingjian，ZHANG Wenping.Numerical simulation of natural convection and radiation heat transfer in 2D enclosure on hybrid grids［J］.Numerical Heat Transfer:Part B，2012，59:116-137.

［14］KIM C，KIM M Y，YU M J，et al.Unstructured polygonal finite volume solution of radiative heat transfer in a complex axisymmetric enclosure［J］.Numerical Heat Transfer:Part B.2010，57:227-239.

［15］MURTHY JY ，MATHUR SR.Radiative heat transfer in axisymmetric geometries using an unstructured finite-volume method［J］.Numer Heat Transfer B，1998，33:397-416.

［16］KIM M Y.Assessment of the axisymmetric radiative heat transfer in a cylindrical enclosure with the finite volume method［J］.Int JHeat Mass Transfer，2008，51:5144-5153.