適用于寬波束的多接收陣SAS波數域成像算法

張學波，唐勁松，鐘何平，張森

(海軍工程大學 電子工程學院，湖北 武漢 430033)

在多接收陣合成孔徑聲吶(SAS)系統［1-2］中，由于聲吶平臺速度和聲速的可比擬性以及成像距離的增大，機載合成孔徑雷達(SAR)中的“停-走-停”假設［3］不再成立，如果仍然忽略了非“停-走-停”［4］的影響，那么遠距離目標可能出現畸變;而相位中心近似(PCA)［5］將多接收陣的信號轉化為收發合置的形式，進而簡化為傳統收發合置SAS成像問題，然而這個轉化會引入延遲誤差，如果不加以補償，會降低近距離目標的成像質量。

Yamaguchi［6］以目標區域中心為參考，用聚焦到目標中心點的相位誤差來代替所有目標區域的誤差，進而在距離彎曲校正過程中完成PCA誤差的補償，這會導致圖像邊沿模糊。Bonifant將這兩個誤差分開來考慮，并通過兩個獨立的相位項［7］來分別補償非“停-走-停”和PCA誤差，然而非“停-走-停”補償未考慮距離向空變性的影響，僅對測繪帶中心實現了精確補償，并且其獨立的誤差分析方法還忽略了兩個誤差之間的耦合性。Callow認為寬波束內不同方向目標的PCA誤差是不同的［8］，并用場景中心點目標方位空變的PCA誤差來近似整個場景的方位空變誤差，這僅對中心點目標實現了精確補償，在邊沿同樣會出現模糊。楊海亮在深入分析這兩類誤差的基礎上，提出了一種適用于寬測繪帶的多接收陣SAS成像方法［4］;汪海濤等在精確時延模型基礎上，也給出了類似的成像方法［9］;然而他們對非“停-走-停”和PCA的補償是以波束中心為參考進行統一補償的。實際上，對于發射陣元的每個發射脈沖，接收陣元接收到的數據對應的是整個波束內所有散射點的回波;波束很窄時，以波束中心為參考進行統一補償能夠取得較好的結果;然而當采用低頻信號進行遠距離探測時波束較寬，系統誤差相對波束內不同方位位置的目標是不同的，如果仍采用窄波束假設進行處理，將會導致圖像旁瓣抬高出現虛假目標、圖像幾何失真和對比度下降。

聲吶在運動過程中觀察目標的視角是不斷變化的，而該側視角與多普勒頻率之間具有一一對應的關系。基于此，文中建立了考慮非“停-走-停”和PCA誤差方位向空變性影響的寬波束模型，二維空域內的距離延遲誤差分析定量說明了本文方法具有顯著的成像處理優勢。另外，針對這兩種誤差精確補償運算量非常大的實際問題，文中提出了一種兼顧補償精度和實現效率的距離向時域分塊-頻域補償的多接收陣SAS波數域成像方法，并采用仿真實驗和實測數據驗證了文中方法的有效性和可行性。

1 多接收陣SAS成像幾何

多接收陣SAS成像幾何如圖1所示，定義r軸為距離維，x軸為方位維，平臺在以速度v沿x軸作勻速直線運動的同時，發射陣元向正側方向發射一個與平臺位置無關的線性調頻信號，其復包絡為

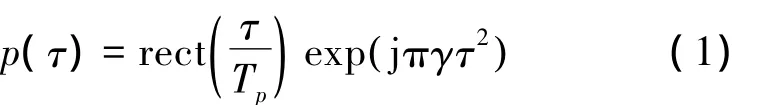
式中:rect(τ)為門函數，Tp表示信號脈沖寬度，γ為調頻率，τ為距離向快變時間。

在發射信號的雙程傳播時間τ*［10］內，接收陣向前運動了vτ*的距離，當平臺速度較大或成像距離較遠時，如果不加以補償將會導致圖像模糊。文獻［4，9］以波束中心為參考，進而采用統一的誤差形式同時補償波束內不同方向上目標的誤差，當波束較窄時，這可以取得較好的結果，然而當波束變寬時，波束內不同位置的目標所對應的誤差也將不同，也就是說系統誤差具有方位向空變性，這里將采用等效相位中心與目標之間的精確距離來近似非“停-走-停”時間，即

式中:θ表示目標和聲吶位置之間的視角，稱之為側視角，根據圖1可以表示為

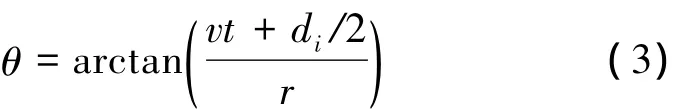
在寬波束條件下，PCA所導致的誤差也具方位向空變性，根據文獻［5］，可以得到隨側視角變化的PCA誤差為

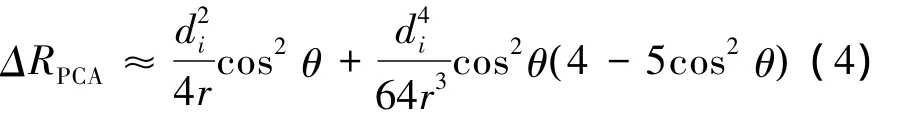
式中:di表示發射陣元與第i個接收陣元之間的距離。

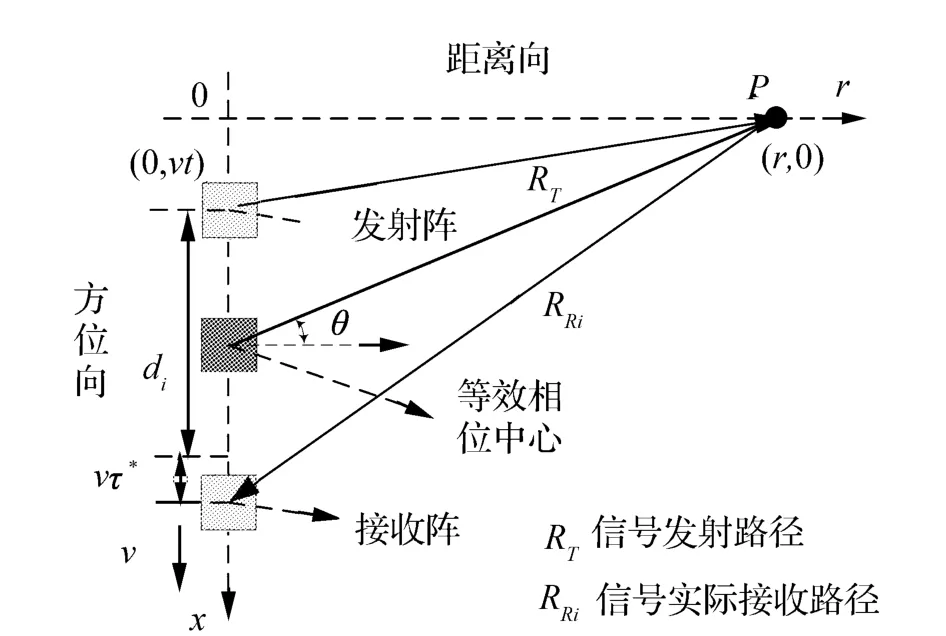
圖1 多接收陣SAS成像示意圖Fig.1 Multi-receiver of SAS

考慮到式(2)和式(4)，將文獻［4］中的近似斜距模型修正為

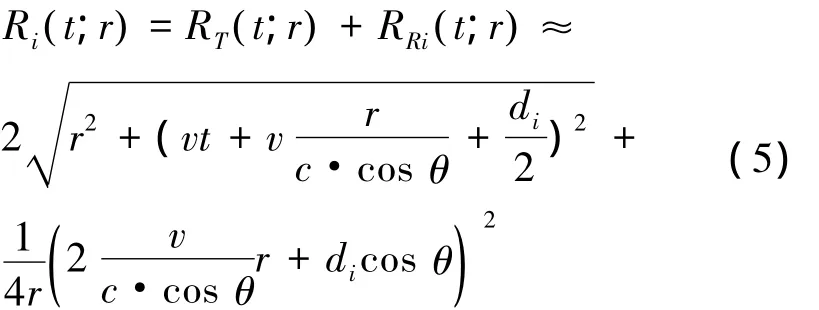
式中:RT( t ;r )=+ (vt)2，表示發射陣元與目標之 間 的 斜 距 歷 程; RRi(t;r)=，表示考慮非“停-走-停”影響時接收陣元與目標之間的斜距歷程。

于是，第i個接收陣元接收到坐標為(r，0)位置處目標的回波信號為

式中:c為水聲聲速;λ為對應于中心頻率fc的波長;wa(t)為方位向窗函數，與濾波加權和收發陣元子系統的波束形狀有關。為簡化分析，在后面的討論中，將重點討論相位項，而忽略包絡的影響。

2 誤差分析

2.1 距離延遲誤差分析

更準確的逼近精確時延模型的快速成像方法可以同時解決SAS圖像高分辨和成像效率的問題，并且還能在一定程度上提高基于相關方法的運動誤差補償的準確性。本節將以文獻［10］中精確的距離模型為標準，在二維空域內對比分析文獻［4］中方法和本文方法的距離延遲誤差(Δr)。

利用多接收陣SAS具有方位向空不變性和距離向空變性的性質［11］，可以將文獻［4］中的一維距離延遲誤差拓展到二維空域內。不失一般性，在一個完整的合成孔徑中心處設置一系列距離空變的點目標，并考察收、發陣元最遠間距分別為0.5 m和3 m情況下的距離延遲誤差。下面分窄、寬波束2種情況分別對比分析文獻［4］和文中方法所產生的誤差。首先來分析窄波束情況下的誤差性能，仿真參數如表1所示。

表1 窄波束情況系統參數Table 1 System parameters in narrow-beam case

在窄波束情況下，當收發陣元最遠間距為0.5 m時，對應于文獻［4］和文中所給出方法的距離延遲誤差如圖2所示;圖3對應于2種方法在收發陣元最遠間距為3 m時的距離延遲誤差。

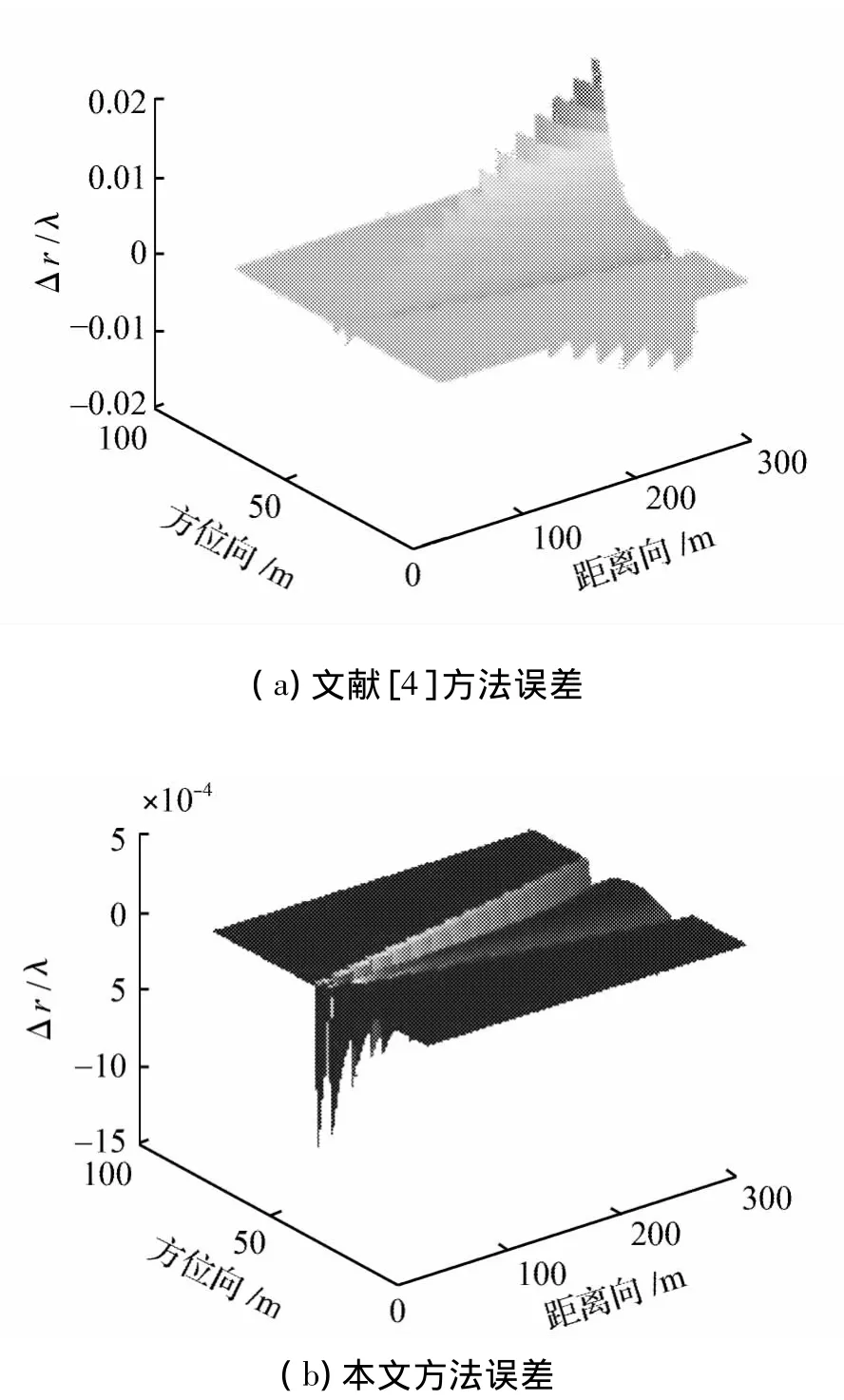
圖2 窄波束情況下收發陣最遠間距為0.5 m時的距離延遲誤差Fig.2 Range propagation delay error in narrow-beam case when the distance between receiver and transmitter is 0.5 m

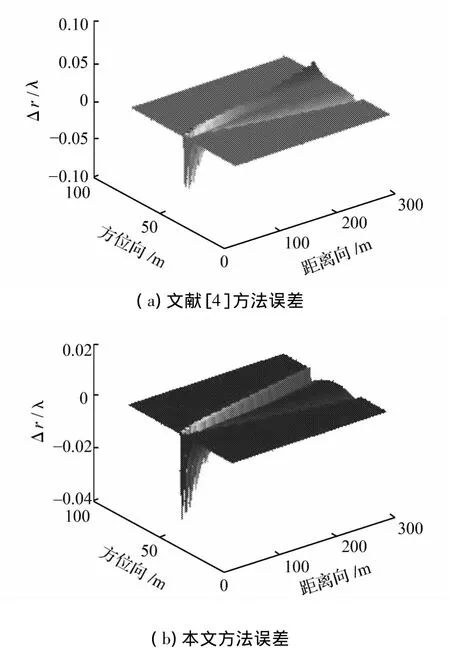
圖3 窄波束情況下收發陣最遠間距為3 m時的距離延遲誤差Fig.3 Range propagation delay error in narrow-beam case when the distance between receiver and transmitter is 3 m

觀察圖2(a)和圖3(a)可以發現，文獻［4］中方法所產生的誤差呈現出楔形狀，這主要是由于忽略了方位向空變的非“停-走-停”誤差以及合成孔徑的距離向空變性所導致的;然而通過比較，文中方法可以較大程度的降低系統誤差，這對成像效果的改善肯定是有一定的促進作用;即便如此，波束較窄時，系統誤差方位向空變性的影響較小，是可以忽略的。

為了對比分析2種方法在寬波束情況下的誤差情況，減小中心頻率和收、發陣元長度以獲得相對較寬的波束，具體的參數如表2所示。

表2 寬波束情況系統參數Table 2 System parameters in wide-beam case

在寬波束情況下，當收發陣元最遠間距為0.5 m時，對應于文獻［4］和文中所給出方法的距離延遲誤差如圖4所示;圖5給出了2種方法在收發陣元最遠間距為3 m時候的距離延遲誤差。

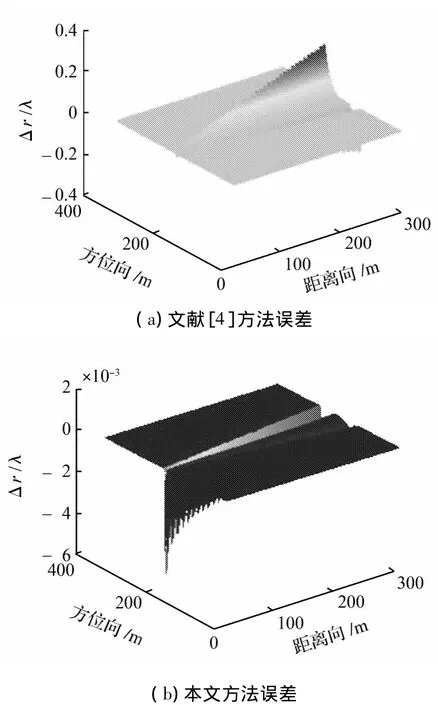
圖4 寬波束情況下收發陣最遠間距為0.5 m時的距離延遲誤差Fig.4 Range propagation delay error in wide-beam case when the distance between receiver and transmitter is 0.5 m.

從圖4和圖5中可以看到:當波束較寬時，文獻［4］方法系統誤差已經受到了方位向空變性的影響，而本文方法通過側視角將系統誤差的方位向空變性聯系了起來，從而具有較好的精確時延模型逼近度。

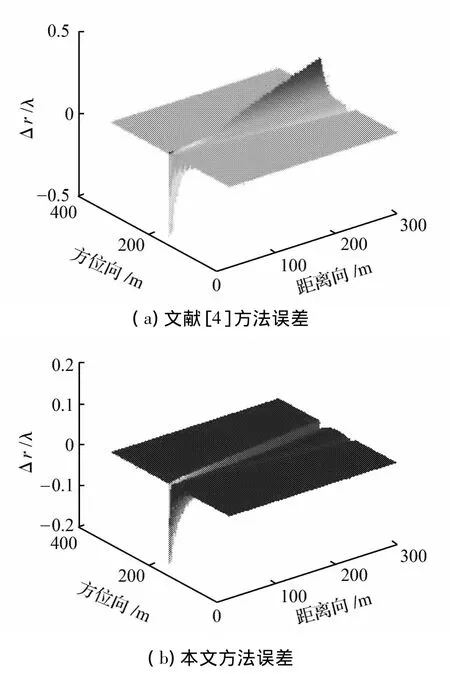
圖5 寬波束情況下收發陣最遠間距為3 m時的距離延遲誤差Fig.5 Range propagation delay error in wide-beam case when the distance between receiver and transmitter is 3 m.

2.2 微距離徙動誤差分析

式(5)最后一項是非“停-走-停”和相位中心近似所產生的誤差項，除了影響多普勒相位外，還將引起距離徙動，稱為微距離徙動量，這里將其重寫為

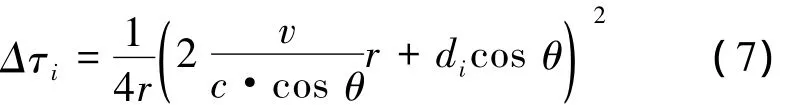
由式(7)可看出這個微距離徙動量是收發陣間距di的增函數，因而將隨著di的增大而增大。

另一方面，求解式(7)關于r的偏導數，并求解下式

可得到滿足微距離徙動量隨距離增大的條件，即

由式(9)可知，在收、發陣元間距di較小時，微距離徙動量將隨距離遞增;然而當收、發陣元間距增大時，隨距離遞增的距離拐點必將會逐漸增大。

在窄波束情況下，對應于表1所示系統參數的微距離徙動誤差如圖6所示，圖6中時延誤差單位ρr表示距離分辨率。

針對于表2所示的寬波束情況，圖7給出了其在距離-多普勒域內的微距離徙動誤差。

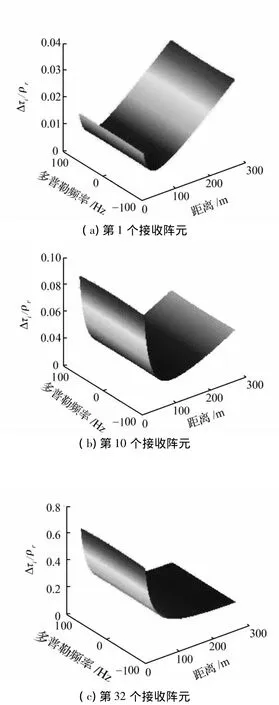
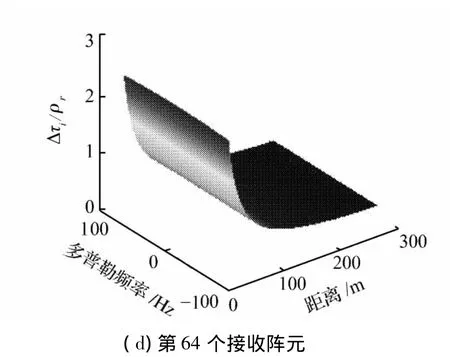
圖6 窄波束情況下微距離徙動誤差Fig.6 Micro range migration error in narrow-beam case

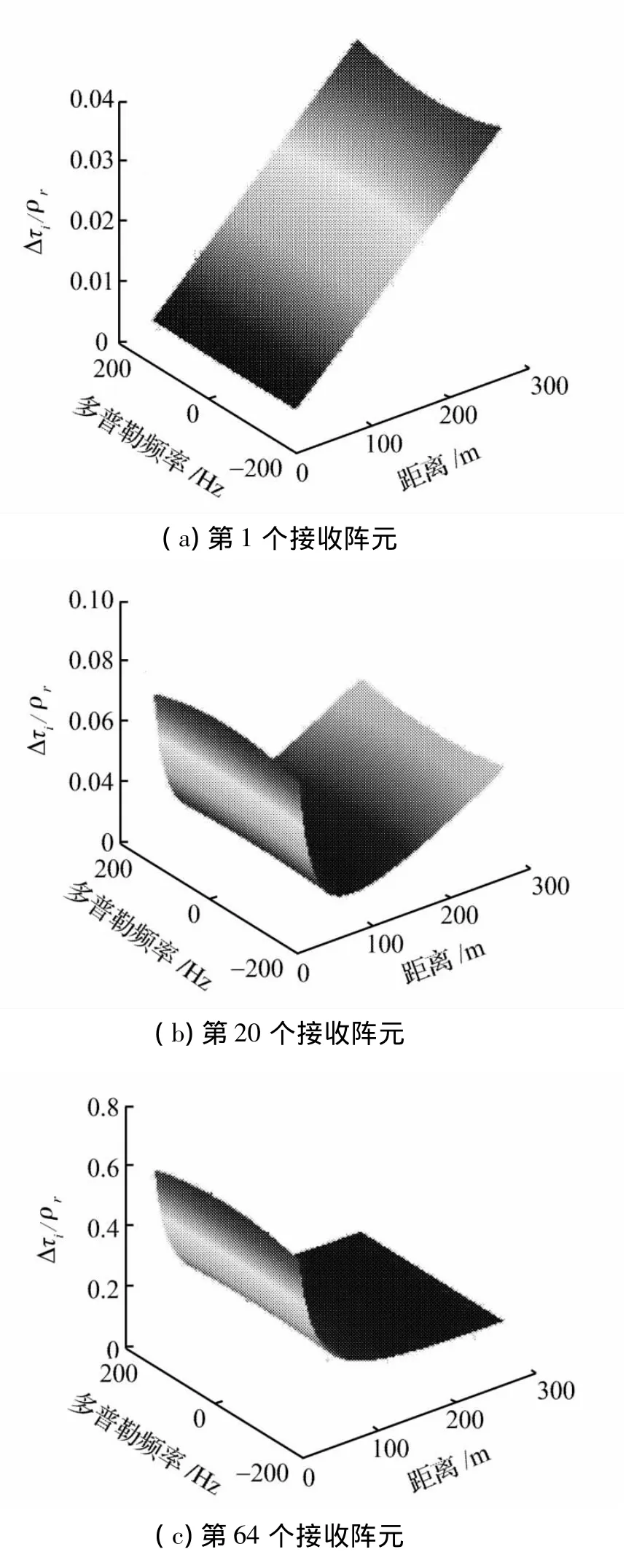
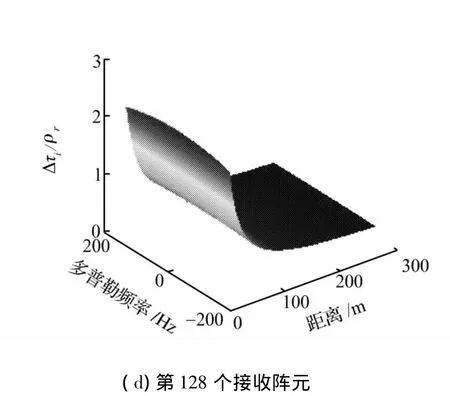
圖7 寬波束情況下微距離徙動誤差Fig.7 Micro range migration error in wide-beam case

從圖6和圖7可以看到:微距離徙動量隨多普勒頻率和距離的不同而變化;當收發陣元間距較小時，微距離徙動量隨距離遞增;隨著收發陣元間距的增大，距離拐點也逐漸增大，當收發陣元距離較大時，這個距離拐點超過了最大測繪距離300 m，從而成為距離的遞減函數，這些結論與式(8)的理論分析是一致的。

另外，圖6和圖7還說明了無論波束的寬、窄，微距離徙動校正(MRCMC)都是多接收陣SAS成像預處理過程中必不可少的一個重要環節。

3 波數域成像算法

波數域成像算法又被稱為ω-k成像算法［11-13］，其處理過程是先將信號變換到波數域，然后通過一致聚焦處理實現參考距離處目標的精確聚焦，最后利用Stolt變換完成非參考距離處目標的距離徙動校正和方位向精確聚焦。然而不同于收發合置SAS的信號處理，多接收陣SAS必須先進行數據預處理，將多接收陣回波信號轉換成收發合置模型下的數據后才能進行成像處理。

利用相位駐留原理，可以得到與式(6)相對應的二維頻域系統函數為

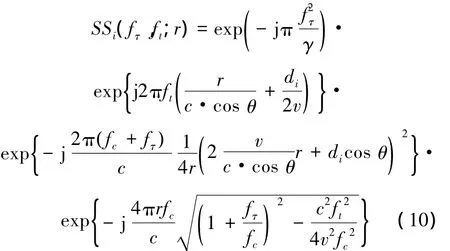
觀察式(10)，在運用經典的收發合置SAS成像算法之前，需要先補償與收發陣元間距有關的相位項，進而將多接收陣SAS下的二維頻域系統函數補償為收發合置SAS模型下的系統函數。下面將詳細介紹預處理的具體步驟。

1)距離向脈壓，其對應的相位函數為

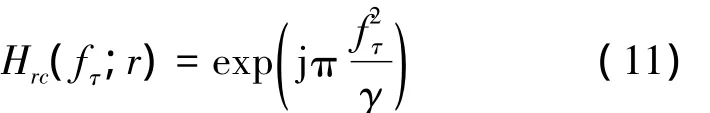
2)補償多普勒相位項。方位向頻域變換后，在距離-多普勒域補償多普勒相位項，其相位補償函數為

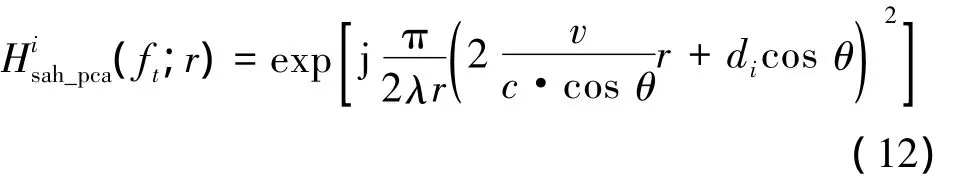
3)微距離徙動校正。微距離徙動主要是由非“停-走-停”和相位中心近似所產生的，如果不加以補償將會使得系統旁瓣升高，圖像幾何失真和對比度下降。實際上，可以通過距離-多普勒域的插值來實現微距離徙動的精確校正，然而運算量卻是非常巨大的。這里采用一種同時兼顧運算量和補償精度的稱之為距離向時域分塊-頻域補償微距離徙動的方法。其思路是近似認為每一個距離向時域分塊數據具有相同的微距離徙動，從而對這一塊數據采用相同的相位函數在頻域通過相乘的方式來實現時延操作。其相乘函數為

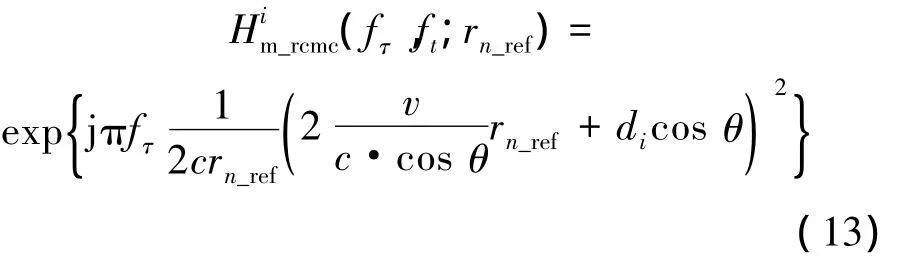
式中:rn_ref表示第n塊數據中的參考距離。

在距離向頻域完成微距離徙動校正后，再在距離向時域取出對應的數據塊進行重組，即可得到微距離徙動校正后的數據。

4)收發分置相位項的補償。在距離-多普勒域補償收發分置相位項，其相位函數為

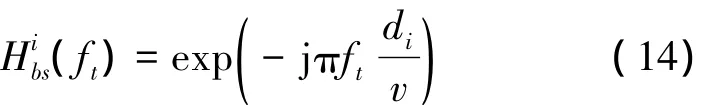
圖8給出了每個接收陣元數據的預處理操作流程。對于每個接收陣元的原始回波都要作圖8所示的預處理操作，然后再將所有接收陣元預處理后的數據在距離-多普勒域進行融合，這樣多接收陣SAS信號便轉化為傳統收發合置SAS數據模型。接下來，可以將這個融合后的數據作為傳統收發合置SAS成像算法的輸入進行成像處理。這里不再贅述RMA算法過程，需要注意的是，數據在Stolt插值之后作方位向IFFT之前，必須進行方位向目標走動校正，這是非“停-走-停”模型下所特有的步驟，其相位函數為

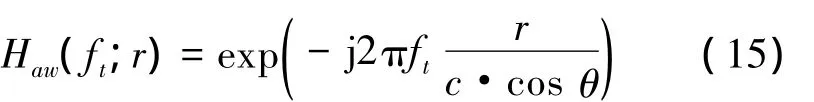
圖8 第i個接收陣元回波預處理流程Fig.8 Block diagram of the preprocessing for theithre ceiver echoed data

4 仿真實驗和實測數據測試

4.1 仿真實驗

對于發射陣元的每個發射脈沖，接收陣元接收到的數據對應的是整個波束內所有散射點的回波。如果僅從這個實際情況出發，那么成像算法預處理中需要考慮到波束內不同目標具有不同的系統誤差，也就是說系統誤差具有方位空變性。實際上，如果令側視角為零，那么文中的寬波束模型便蛻化為文獻［4］中的窄波束假設，由此可見窄波束假設是一種近似處理，僅是文中寬波束模型的一個特例而已。本節將針對2.1節表1、2所示的窄波束、寬波束系統分別進行仿真研究，以驗證文中方法的有效性。

首先研究窄波束情況(系統參數對應于表1)下文獻［4］中方法和文中方法的成像性能。在近距離和遠距離處分別設置坐標為(102 m，6 m)和(280m，50m)的理想點目標。圖9為目標成像后的方位向剖面圖。

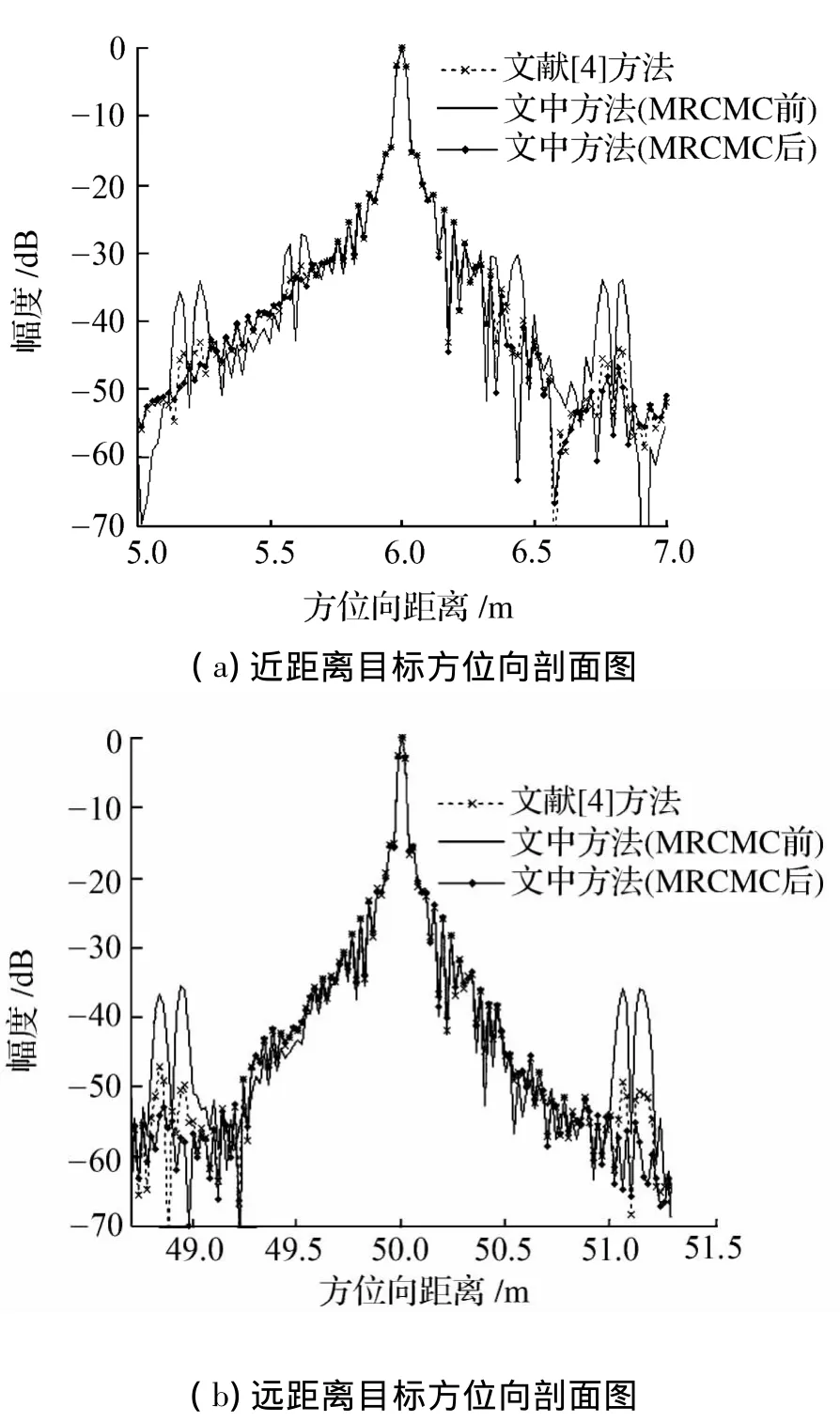
圖9 窄波束情況點目標方位向剖面圖Fig.9 Azimuth slices for a point target in narrow-beam case

從圖9中可以看到:相對文獻［4］方法，文中方法還是具有一定的改善效果，但是考慮到系統誤差方位向空變性的影響比較小，因而在實際中可以忽略方位向空變性的影響。對比圖9文中方法微距離徙動校正前后的成像結果，可以看到微距離徙動校正確實是多接收陣SAS成像中必不可少的步驟。

獲得文中方法在窄波束情況下的聚焦性能后，再來研究文中方法在寬波束情況下的成像性能。同樣在近距離和遠距離處分別設置坐標為(102 m，18 m)和(280 m，75 m)的理想點目標。目標聚焦后的方位向剖面圖如圖10所示。

對比圖10成像結果，可以明顯看到文中方法在寬波束條件下成像處理的優勢。同時也說明了寬波束情況下微距離徙動校正的必要性，吻合于2.2節的結論。觀察圖10(d)，文獻［4］的方法使目標存在一個較小的偏移，另外其主瓣已經存在一定程度的畸變，而本文方法成像結果基本沒有任何畸變。

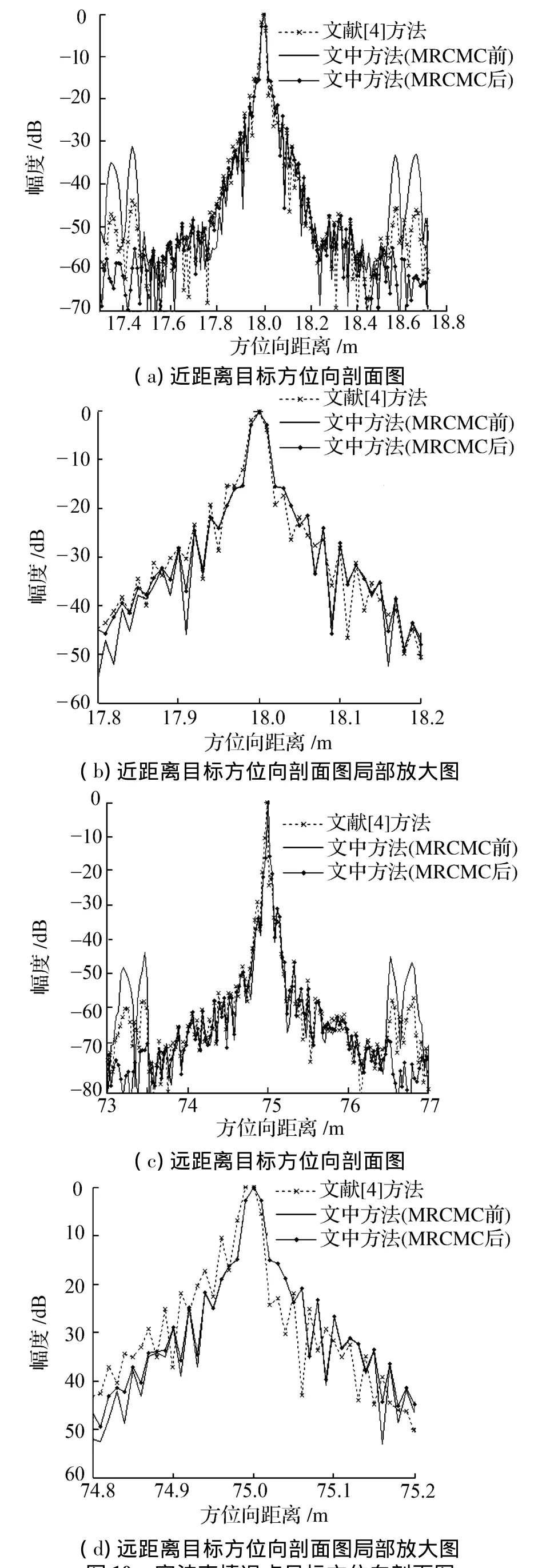
圖10 寬波束情況點目標方位向剖面圖Fig.10 Azimuth slices for a point target in wide-beam case

4.2 實測數據測試

本小節主要采用2010年7月ChinSAS-150產品在浙江淳安千島湖試驗中的某航次實測數據進一步驗證文中所提出方法的正確性，其試驗參數為:發射信號中心頻率為150 kHz，信號帶寬為20 kHz，信號脈寬為20ms，脈沖重復時間為0.32 s;接收陣元方位向實孔徑長度為0.04m，參與成像的接收陣元個數為40個，發射陣元方位向實孔徑為0.08m，聲吶載體速度為2.5m/s。

圖11 實測數據成像結果Fig.11 Imaging results of real data

試驗場景為千島湖湖底地形地貌，在數據處理前，先完成各接收陣數據的兩兩疊加處理，即1+2，2+3，…。成像結果如圖11所示，其中圖11(a)為文獻［4］方法處理后的成像結果，圖11(b)為本文方法處理后的成像結果。對比兩圖可以發現:沿方位向，圖11(b)在兩端邊緣10 m的范圍內具有更加清晰的重構場景。另外，需要說明的是該系統所對應的波束較窄，與表1所示參數相當;因此文中方法的優勢還有待于下一代高分辨SAS系統的進一步驗證。

5 結束語

窄波束假設的處理前提是系統誤差相對波束內任何方位位置的目標均近似相同，即不考慮系統誤差的方位空變性。文中根據方位向側視角和多普勒瞬時頻率之間的一一映射關系，建立的寬波束模型兼容窄波束假設處理方法，很好地解決了系統誤差的方位空變性問題。

文中針對寬波束模型下的微距離徙動校正耗時量較大的問題，提出了一種距離向時域分塊-頻域補償的多接收陣SAS成像處理方法。該方法同時兼顧了補償精度和實現效率，利用二維誤差分析和仿真實驗來驗證文中方法的優勢，并采用實測數據來檢驗文中方法的可行性;然而其優勢還有待于實驗數據的進一步測試。

［1］孫大軍，田坦.合成孔徑聲吶技術研究［J］.哈爾濱工程大學學報，2000，21(1):51-56.SUN Dajun，TIAN Tan.The study of synthetic aperture sonar(SAS)technique［J］.Journal of Harbin Engineering University，2000，21(1):51-56.

［2］HAYESM P，GOUGH P T.Synthetic aperture sonar:a review of current status［J］.IEEE Journal of Oceanic Engineering，2009，34(3):207-224.

［3］SOUMEKH M.Synthetic aperture radar signal processing with matlab algorithm［M］.New York:Wiley，1999:56-57.

［4］楊海亮，張森，唐勁松.寬測繪帶多接收陣合成孔徑聲吶成像處理方法［J］.系統仿真學報，2011，23(7):1424-1428.YANG Hailiang，ZHANG Sen，TANG Jinsong.Study on simulation of multiple-receiver synthetic aperture sonar imagery based on wide swath［J］.Journal of System Simulation，2011，23(7):1424-1428.

［5］BELLETTINIA，PINTO M A.Theoretical accuracy of synthetic aperture sonar micronavigation using a displaced phase-center antenna［J］.IEEE Journal of Oceanic Engineering，2002，27(4):780-789.

［6］YAMAGUCHI I.A technique of multi-aperture transmitting receivering on synthetic aperture sonar［J］.Electronics and Communications in Japan，1999，82(3):66-73.

［7］BONIFANTW W.Interferometric synthetic aperture sonar processing［D］.Atlanta:Georgia Institute of Technology，1999:38-42.

［8］CALLOW H J.Signal processing for synthetic aperture sonar image enhancement［D］.Chrirstchurch:University of Canterbury，2003:64-68.

［9］汪海濤，唐勁松，苑秉成.多子陣SAS逐線成像算法研究［J］.哈爾濱工程大學學報，2009，30(7):820-823.WANG Haitao，TANG Jinsong，YUAN Bingcheng.Research on a multi-receiver synthetic aperture sonar imaging algorithm based on FFT［J］.Journal of Harbin Engineering University，2009，30(7):820-823.

［10］唐勁松，張春華，李啟虎.多子陣合成孔徑聲吶逐點成像算法［C］//中國科學院聲學研究所1999年青年學術交流會.北京，中國，1999:235-239.

［11］BAMLER R.A comparison of range-Doppler and wavenumber domain SAR focusing algorithms［J］.IEEE Transactions on Geoscience and Remote Sensing，1992，30(4):706-713.

［12］PRATIC，ROCCA F，GUAMIERIA M.Seismic migration for SAR focusing:interferometrical application ［J］.IEEE Transactions on Geoscience and Remote Sensing，1990，28(4):627-639.

［13］REIGBER A，ALIVIZATOSE，POTSISA，et al.Extended wavenumber-domain synthetic aperture radar focusing with integrated motion compensation ［J］.IET Radar，Sonar and Navigation，2006，153(3):301-310.