壓電結構系統機電耦合的強化與多階共振抑制

李 琳 劉 學

(北京航空航天大學 能源與動力工程學院，北京100191)

20世紀90 年代初 Hagood 等人[1－2]提出以壓電材料為媒介將振動系統的動能通過電路中的電阻轉化為熱能耗散掉，從而形成一種新的振動阻尼-壓電阻尼的學術思想.這一學術思想一經問世，就受到國內外研究人員的廣泛關注[3－4].從那時起，人們研究與設計了各種與壓電材料相連接的電路，以尋求獲得最佳振動控制效果.基于該思想所開發(fā)的振動阻尼被稱為壓電分支電路阻尼;對應的方法、技術被稱為壓電分支電路方法、技術.

壓電分支電路既可用于被動振動控制也可用于主動振動控制和半主動振動控制[5－7].無論何種振動控制，引入壓電材料的結構、系統的機電耦合程度都是影響控制效果的一個重要因素.在現有的文獻中，提高系統機電耦合程度的研究，主要分為電路設計和結構系統中壓電材料的分布設計.電路設計是通過將不同的電感和“負電容”[8－9]引入電路中，達到提高系統機電耦合程度的目的.壓電材料的分布設計是指通過設計壓電材料的粘貼位置，提高系統模態(tài)機電耦合程度.該種方法的主要手段是通過數值計算得到最佳粘貼位置:Carlos等人利用拓撲優(yōu)化算法，計算了平板振動模型中，每一階模態(tài)對應的最佳壓電片的粘貼位置和形狀[10];Belloli等人利用有限元方法分析了一個汽車部件上如何改變壓電片的粘貼位置達到最大機電耦合系數，并通過實驗驗證[11];Liao等人以壓電懸臂梁為例，驗證當一片壓電片粘貼在模態(tài)彎矩變形最大的地方，可以使機電耦合效果達到最大[12];與文獻[12]相近，Vasques通過壓電片電極的形狀設計，提高機電耦合效果[13].但是這些方法一般只針對某一階模態(tài)振動的控制，固定的壓電片形狀與粘貼位置也限制了多階模態(tài)的振動控制.

作者通過對壓電懸臂梁的理論模型研究發(fā)現，除了壓電材料的材料特性以及幾何尺寸外，改變壓電材料的電極分布形式和電極連入電路方式也可以提高系統的機電耦合程度.為了使多階振動模態(tài)均具有較高的機電耦合程度，再將“選通電路”的思想[14－15]引入到電極與分支電路的連接電路中，即可實現系統的多階共振抑制.本文給出獲得這一研究結論的過程及數值驗證.

1 壓電懸臂梁耦合動力學方程及其解式

本文采用的壓電懸臂梁模型如圖1所示.主結構梁的上下表面貼有壓電片，壓電片將結構梁全部覆蓋，上下兩層壓電片的尺寸完全相同;該梁模型滿足歐拉梁假設.其中下層壓電片(PZT2)外接交流電源作為模型激振源，上層壓電片(PZT1)用于連接阻抗為Z的外接電路對系統進行振動控制.

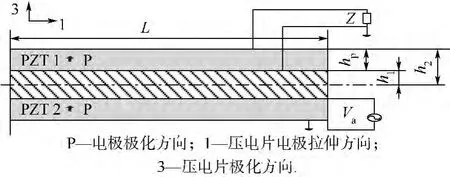
圖1 壓電懸臂梁模型Fig.1 Piezoelectric cantilever beam model

沿梁長方向取微段dx建立動力學平衡方程，在考慮截面內力與變形的關系時分別應用梁主體材料的本構關系和壓電材料的本構關系，可得壓電懸臂梁模型的動力學方程(忽略結構阻尼):

式中

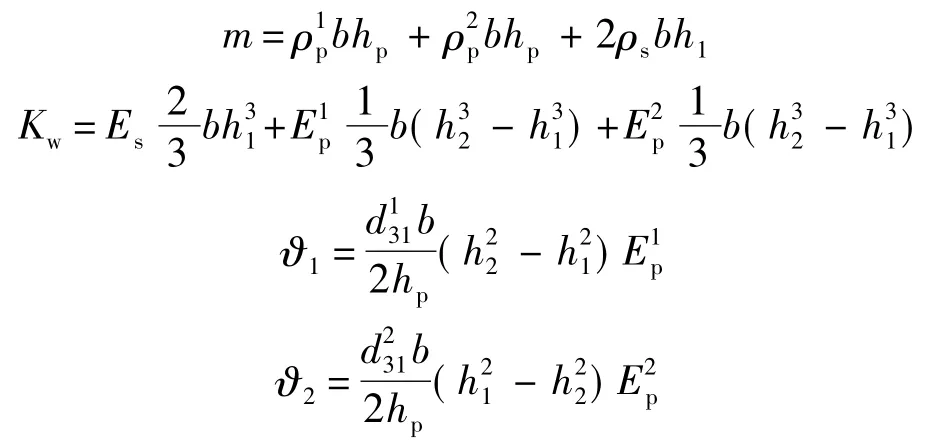
Kw為壓電梁的抗彎剛度;m為壓電梁的線密度;下標s表示與結構相關;下標p表示與壓電材料相關;上標1或2用于區(qū)分上下層壓電片參數;例如用E表示材料的彈性模量時，Es則為梁本體結構材料的彈性模量;分別為上下層壓電片材料的彈性模量;w為懸臂梁的橫向振動位移;b為梁的截面寬度;h為梁的截面高度;V1為分支電路的電壓;Va為(用于激振的)外接電源的電壓;d31為壓電材料機電耦合系數.

將壓電材料的本構關系與電路中電流與電量的關系相結合，可得電路部分的方程:

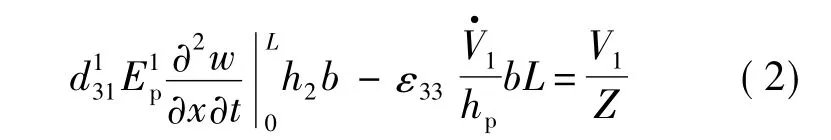
式中，ε33為壓電材料的介電常數;Z為電路阻抗.

方程(1)和方程(2)均包含有力學變量w(x，t)和電學變量V1(t)，二者聯立構成的耦合方程組即是壓電懸臂梁的機電耦合動力學方程.在下面的分析中為了更好地理解該系統的內在規(guī)律，以不考慮耦合效應的結構參數和電路參數作為參考，引入如下無量綱變量:

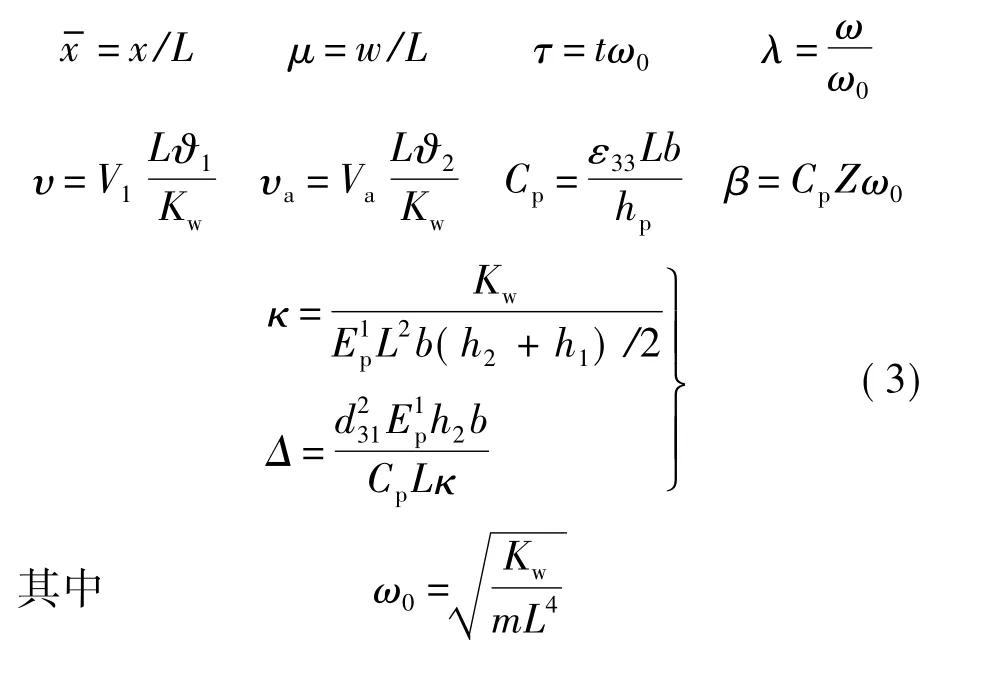
以無量綱變量表示的方程(1)、方程(2)分別為

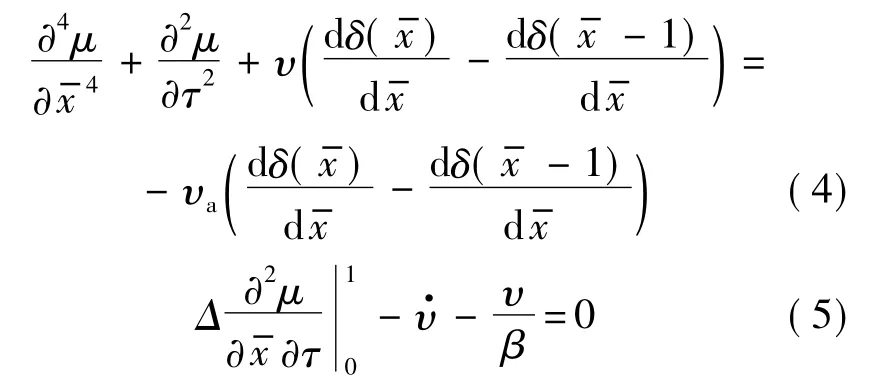
為了獲得耦合方程組(4)、方程組(5)的解，設響應μ具有如下形式:

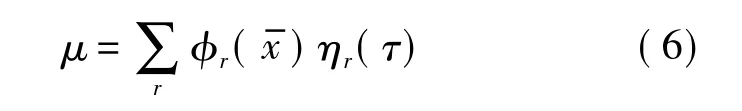
式中φr為梁的振型函數，方程(4)的齊次解.

對于具有如下形式的激勵υa:

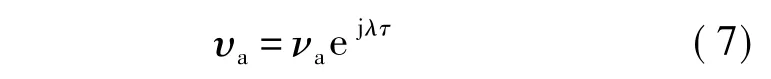
設

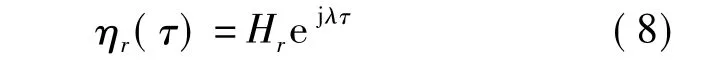
則系統的響應為

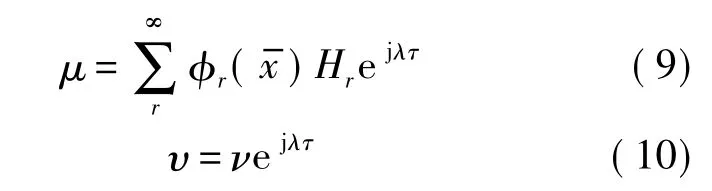
為了確定 Hr和 ν，分別將表達式(9)和式(10)代入到方程(4)和方程(5)，并進行正交性變換，可得

記

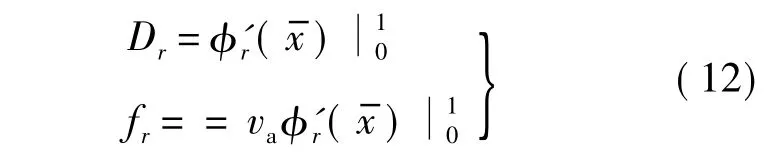
于是壓電系統在模態(tài)空間的方程可以寫為

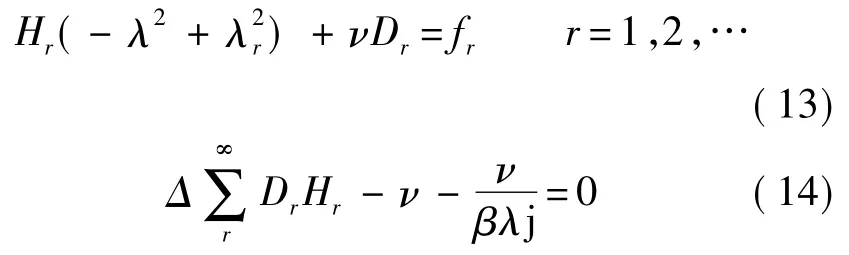
將式(13)、式(14)聯立求解可得分支電路中的(無量綱)電壓響應幅值:

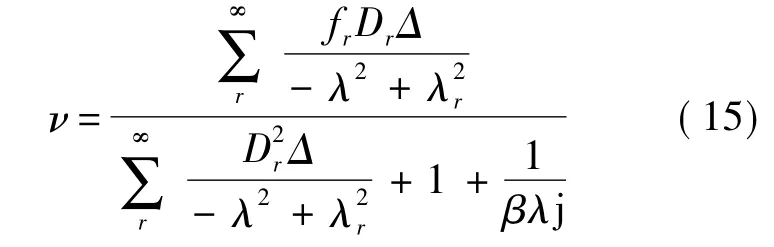
以及各模態(tài)空間的位移響應幅值:

再將上述結果代入式(9)即得到壓電懸臂梁的無量綱位移響應:

2 壓電懸臂梁的模態(tài)機電耦合函數

2.1 模態(tài)機電耦合函數的提出

為了有效消減結構的振動，應設法使結構振動位移有較小的值，分支電路中的電壓有較大的值(這意味著有較多的機械能轉變成了電能，從而可通過電路消耗掉).仍以壓電懸臂梁為例，從壓電懸臂梁的電壓響應ν的幅值表達式和振動位移μ的表達式可以看出，在共振區(qū)(λ→λr)，ν和μ的共振響應幅值大小主要由Dr和Δ兩個系數決定(由式(12)可知fr正比于Dr);Δ已在式(3)中給出:

可以看出，Δ只與壓電材料以及主結構材料和幾何尺寸相關，這里稱其為材料機電耦合系數.

Dr的表達式為:.

仔細分析式(15)可以發(fā)現，當外接電阻β無窮大且激振頻率接近某一階共振頻率時，壓電片電壓響應的大小與正負(相對激勵電壓)與直接相關.由此想到，如果將電極適當離散，使各離散點的位置對應不同的模態(tài)時，電壓響應為正的電極與電壓響應為負的電極連接方法相反，有可能獲得提高該階模態(tài)機電耦合函數值的效果.

2.2 具有離散電極壓電懸臂梁的模態(tài)機電耦合函數

對圖1所示的壓電懸臂梁，將壓電片1的電極進行離散，設第 i片電極的位置為 xi－1＜x＜xi，每一片電極的電壓表示為Vi，電量為，電極的連接方式分為正接和反接兩種:P代表正接，N代表反接.所有電極都連入分支電路，公共端的電壓為V.

定義連接方式函數δ(NP):

則存在如下關系式:

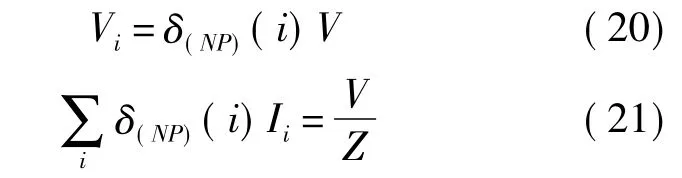
于是電極離散后的系統耦合動力學方程成為

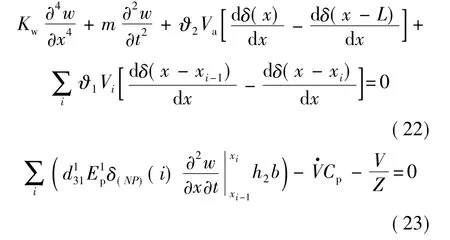
對應的無量綱化方程為

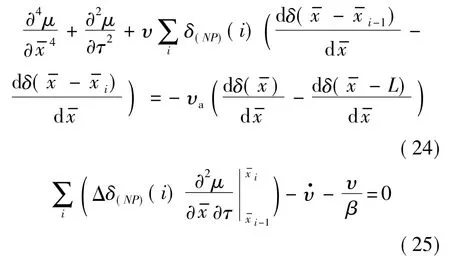
按照與式(4)～式(12)相同的過程對該方程進行求解，可以得到

將其用Dr代替時，即取

則得到與式(13)、式(14)相同的表達式.由此得出如下結論:離散電極壓電系統的模態(tài)機電耦合函數等于各離散電極對應部分的模態(tài)機電耦合函數按照該電極連入電路方式進行疊加之和.式(28)表明，對于某一確定的振型，Dr的大小與電極的分布位置和電極的連接方式相關.這一結論給出的提示是，可通過調整電極的分布位置和連接方式，使該階模態(tài)機電耦合函數具有希望值.

綜上所述，壓電結構的機電耦合程度取決于兩類因素:與材料及幾何尺寸相關的材料機電耦合系數Δ，以及系統的模態(tài)機電耦合函數Dr，該函數值由壓電片電極分布位置(離散電極的坐標xi)和電極連入電路的方式(δ(NP)(i))決定;壓電片電極分布位置和連接方式一定，對應于每一階模態(tài)的機電耦合函數值隨之確定.

表1給出對應上述結論的一組數值結果:對于材料相同、幾何尺寸相同的懸臂梁，采用3種不同的壓電片電極分布和電極連接方式時，第3階模態(tài)機電耦合函數值的變化.

表1 具有不同電極連接方式的模態(tài)機電耦合函數值Table 1 Value of modal electromechanical function at different connection methods of piezoelectric cantilever beam

表1表明，不同的電極分布形式及連接方式可以使系統的模態(tài)機電耦合函數值發(fā)生數倍的變化.顯然對應于每一階模態(tài)，通過對模態(tài)機電耦合函數的優(yōu)化，都可找到電極的最佳分布位置和最佳連接方式，使該階的機電耦合函數具有最大值.

3 多階共振抑制

如果在減振的頻率范圍內每一階模態(tài)的機電耦合函數都具有較高的值，則可以有效抑制系統在該頻率范圍內的振動.然而Dr的表達式說明，調整電極的分布和連接方式只能保證某一階模態(tài)的機電耦合函數具有最大值.為了解決這一問題，使系統在各階模態(tài)頻率振動時的機電耦合函數均具有較大的值，達到多階共振抑制的目的，這里引入電學中的選通電路設計思想.選通電路是指阻抗為 Zab(ωa，ωb)的電路，在頻帶(ωa，ωb)范圍內為通路，而遠離該頻帶時，該電路為斷路.將該種電路引入壓電系統中，即可以實現當系統處在設計共振的頻段內時，每一片電極的連接方式都是最適合的連接方式.含選通電路、具有離散電極的壓電懸臂梁模型如圖2所示.

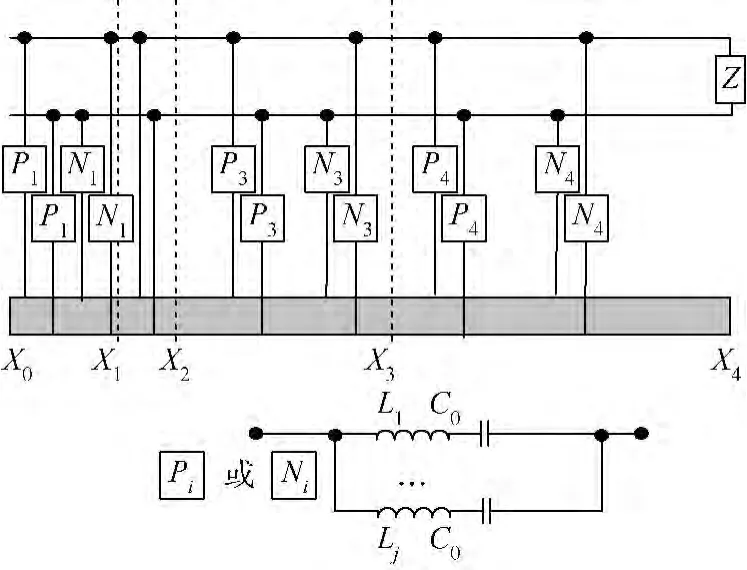
圖2 含選通電路、具有離散電極的壓電懸臂梁模型Fig.2 Distribute electrode piezoelectric cantilever beam with‘current flowing’electric circuits

電感Lj滿足條件:

式中，ωj為被控共振的頻率，對應第i片電極的各模塊的阻抗為ZPi或ZNi.第i片電極的電路如圖3所示.

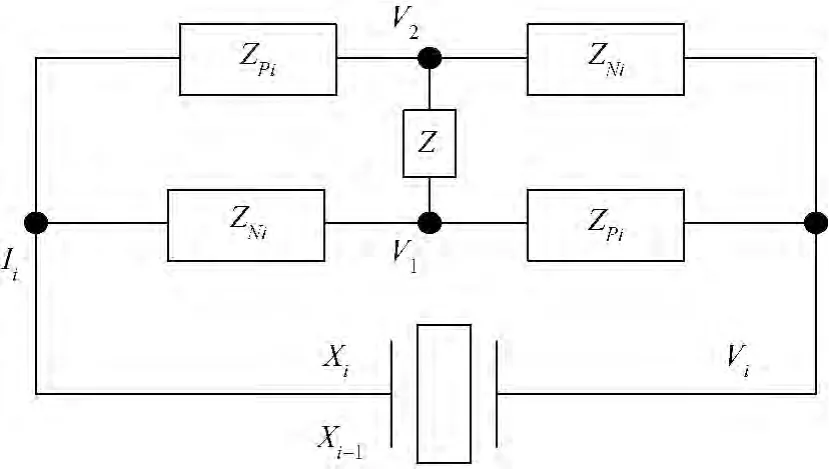
圖3 第i片電極的電路形式Fig.3 Electric circuit of the ith electrode

含有選通電路的壓電懸臂梁的機電耦合動力學方程(該方程的導出用到了選通電路電壓與電流的關系)如下:

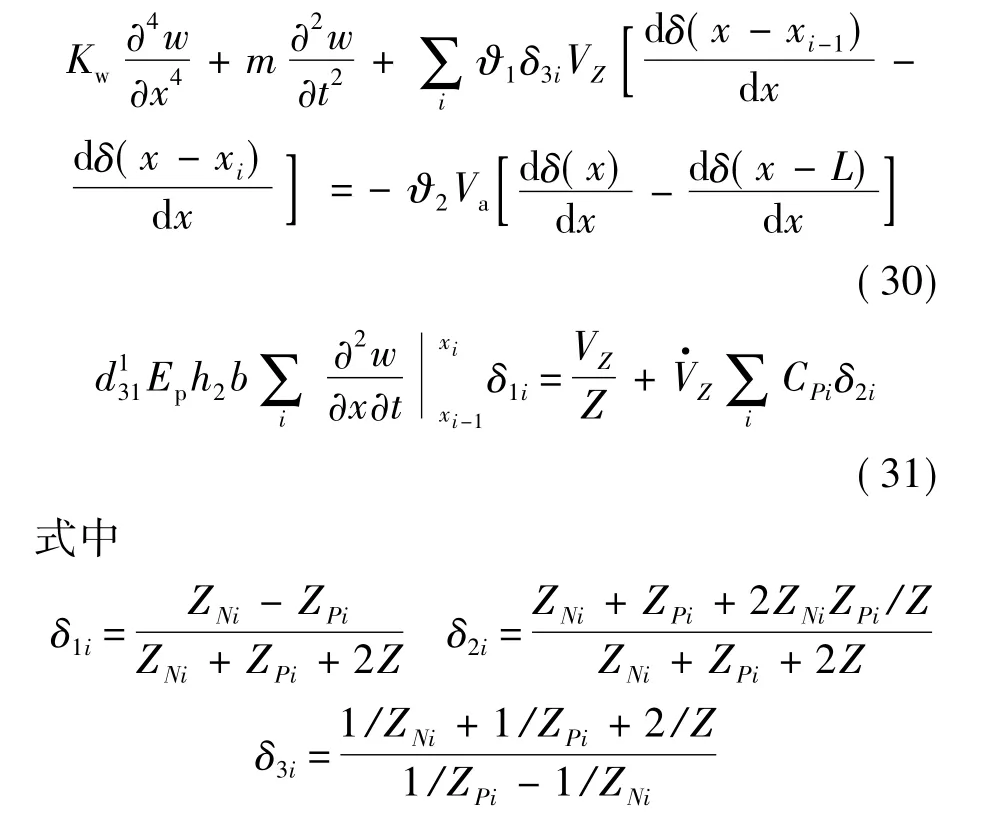
對方程(30)、方程(31)采用與式(4)～式(12)相同過程求解，可以得到

與方程(26)和方程(27)對比，可以發(fā)現，加權系數 δ1i，δ2i，δ3i取代了 δ(NP)的作用，使連接方式隨激振頻率變化，正是這種變化使電極按設計狀態(tài)導通外接電路，因而可以通過對模態(tài)機電耦合函數的優(yōu)化實現同時提高多階模態(tài)機電耦合函數值、達到多階模態(tài)振動控制的效果.

下面給出對于圖2所示壓電懸臂梁進行前3階共振位移控制的數值驗證實例.將電極離散為4段，表1中給出的離散點的位置即是對模態(tài)機電耦合函數優(yōu)化的結果.分支電路中僅包含單值(無量綱)電阻β=0.016 2(這個阻值為第3階共振最佳抑制效果的電阻值).其中各選通電路所控制的共振階次如表2所示.

表2 各選通電路控制的共振階次Table 2 Control modes for each‘current flowing’circuit

求解方程(32)和方程(33)可以得到該壓電懸臂梁端部的位移幅頻響應曲線，如圖4所示，圖中橫坐標為無量綱頻率，縱坐標為響應幅值.為了便于比較，圖4中同時給出該壓電懸臂梁短路和連續(xù)電極兩種工況下的端部位移響應曲線.表3給出對應前3階共振峰值消減的數值效果.

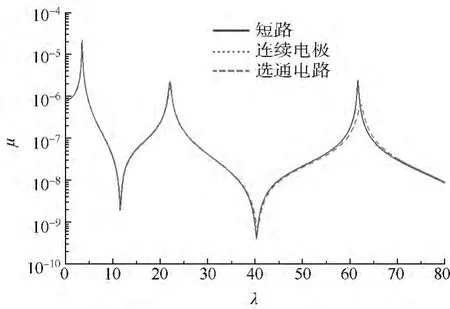
圖4 壓電懸臂梁端部位移幅頻響應曲線Fig.4 Amplitude-frequency of the displacement of the beam tip for three kinds of circuits

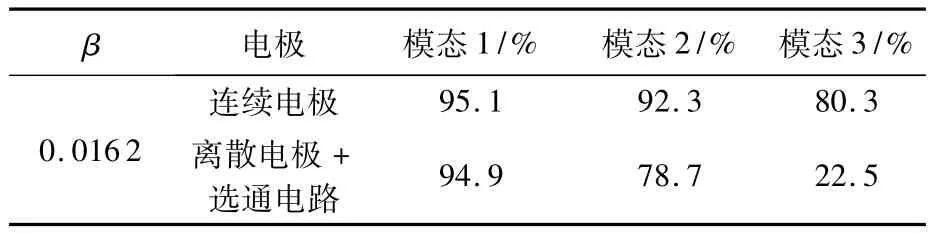
表3 兩種電路狀態(tài)響應峰值與短路響應峰值之比Table 3 Ratios of the amplitudes in two design methods to the one in short circuit

共振峰值的消減程度反映了模態(tài)阻尼(即模型中的壓電阻尼對該模態(tài)貢獻)的大小;從圖4和表3可以看出，帶有選通電路的壓電懸臂梁除了第1階模態(tài)的壓電阻尼與連續(xù)電極模型相同(反映為共振峰值基本相同)，第2、第3階模態(tài)的壓電阻尼效果明顯大于連續(xù)電極模型.這說明這種設計方法可以同時提高壓電結構的多階模態(tài)振動抑制效果.這一效果的本質在于這一方法同時提高了該壓電系統的多階模態(tài)機電耦合程度.這對于壓電系統的振動控制至關重要.上述設計方法通過提高多階模態(tài)機電耦合函數值，實現了壓電分支電路對多階共振的抑制.本節(jié)只以單獨阻值的分支電路為例，證明了該種設計方法可以有效地提高多模態(tài)的機電耦合函數值.該方法也適用于其他壓電振動控制.

4 結論

1)將壓電片的電極離散，并進行不同方法的連接，可以導致系統不同模態(tài)的機電耦合程度發(fā)生改變，這一現象可以用模態(tài)機電耦合函數來描述;

2)對壓電片電極的分布及連接方式進行設計，并與選通電路的設計結合，對多模態(tài)機電耦合函數進行優(yōu)化，可實現多階共振抑制;

3)電極的分布及連接方式設計的核心是確定對應共振狀態(tài)下的電壓響應為正的電極與電壓響應為負的電極進行反連或正連.

上述研究結論與方法雖然是依據懸臂梁模型得出，但是也可以適用于一般結構.對于一般結構，除了仔細設計壓電片的位置以外，可按照本文提出的方法，根據模態(tài)電壓響應設計電極連接方式，再通過共振頻率設計選通電路，優(yōu)化結構的多模態(tài)機電耦合函數，進而實現結構的多階共振抑制.

References)

[1]Hagood N W，von Flotow A.Damping of structural vibrations with piezoelectric materials and passive electrical networks[J].Journal of Sound and Vibration，1991，146(2):243 －268

[2]Crawley E F，de Luis J，Hagood N W，et al.Development of piezoelectric technology for applications in control of intelligent structures[M].Atlanta，GA:IEEE，1988

[3]Moheimani S O R.A survey of recent innovations in vibration damping and control using shunted piezoelectric[J].IEEE Transactions on Control Systems Technology，2003，11(4):482－499

[4]姚軍，李岳鋒.壓電薄板的建模和阻尼的準獨立模態(tài)控制[J].航空學報，2000，21(2):159 －163

Yao Jun，Li Yuefeng.Modeling of piezoelectric thin plates and quasi-independent modal control for damping[J].Acta Aeronautica et Astronautica Sinica，2000，21(2):159 －163(in Chinese)

[5]王建軍，李其漢.具有分支電路的可控壓電阻尼減振技術[J].力學進展，2003，33(3):389 －403 Wang Jianjun，Li Qihan.Recent advances of vibration damping and control using piezoelectric materials with shunted circuits[J].Advances in Mechanics，2003，33(3):389 － 403(in Chinese)

[6]陳偉民，管德，李敏，等.壓電驅動器用于薄板型結構振動主動控制研究[J].航空學報，2001，22(2):109 －112

Chen Weimin，Guan De，Li Min，et al.Active vibration control of thin plate with piezoelectric actuators[J].Acta Aeronautica et Astronautica Sinica，2001，22(2):109 －112(in Chinese)

[7]Guyomar D，Richard C，Mohammadi S.Semi-passive random vibration control based on statistics[J].Journal of Sound and Vibration，2007，307(3-5):818 －833

[8]Park C H，Inman D J.Enhanced piezoelectric shunt design[J].Shock and Vibration，2003，10(2):127 －133

[9]De Marneffe B，Preumont A.Vibration damping with negative capacitance shunts:theory and experiment[J].Smart Materials and Structures，2008，17(3):35015

[10]Carlos N E，Kikuchi S.Design of piezoelectric transducers using topology optimization[J].Smart Materials and Structures，1999，8(3):350 －364

[11]Belloli A，Ermanni P.Optimum placement of piezoelectric ceramic modules for vibration suppression of highly constrained structures[J].Smart Materials and Structures，2007，16(5):1662－1671

[12]Liao Y B，Sodano H A.Optimal placement of piezoelectric material on a cantilever beam for maximum piezoelectric damping and power harvesting efficiency[J].Smart Materials and Structures，2012，21(10):105014

[13]Vasques C M A.Improved passive shunt vibration control of smart piezo-elastic beams using modal piezoelectric transducers with shaped electrodes[J].Smart Materials and Structures，2012，21(12):125003

[14]Hollkamp J J.Multimodal passive vibration suppression with piezoelectric materials and resonant shunts[J].Journal of Intelligent Material Systems And Structures，1994，5(1):49 －58

[15]Behrens S，Moheimani S O R.Current flowing multiple-mode piezoelectric shunt dampener[C]//Proceedings of SPIE-the International Society for Optical Engineering.Bellingham，WA:SPIE，2002，4697:217 －226

[16]Erturk A，Inman D J.A distributed parameter electromechanical model for cantilevered piezoelectric energy harvesters[J].Journal of Vibration and Acoustics-Transactions of the ASME，2008，130(4):041002-1 －15