腫瘤細胞的生長模型與預測治療

張鵬鴿，朱佑彬，高淑萍

(西安電子科技大學數學與統計學院，西安 710071)

癌癥是一大類惡性腫瘤的統稱。癌細胞具有無限制、無止境增生的特點，而且腫瘤細胞的生長會大量消耗患者體內的營養物質，同時，還會局部浸入周圍正常組織甚至經由體內循環系統或淋巴系統轉移到身體其他部分，對人類的生命具有極大威脅。因此，針對這一問題，本文恰當地建立腫瘤細胞增長的數學模型，制定合理的措施以利于及早發現病癥并及早治療，提高存活率，這也是攻克癌癥的關鍵，更是現代醫學的重要課題。

首先，我們建立腫瘤細胞的增長模型。在此，先考慮癌癥細胞的生長模型，根據模型的生長函數得出腫瘤細胞的倍增次數，再根據倍增次數推出腫瘤細胞的增長函數，并作出圖像，求出腫瘤細胞的增長模型;其次，在求解出來模型的基礎上，制定出合理的措施，使得病人盡可能早地發現癌癥，或者使癌癥患者盡可能地延長壽命，此時，則建立優化模型，目標函數是費用少，發現早。

1 資料與方法

由細胞增長的研究可知腫瘤細胞增長的規律特點:①按照現有手段，腫瘤細胞數目超過一定數量時，或腫瘤體積達到一定大小時，臨床才能觀察到;②在腫瘤生長初期，每經過一定的時間，腫瘤細胞的數目就增加一倍;③在腫瘤生長后期，由于各種生理條件的限制，腫瘤細胞數目逐漸趨向某個穩定值。

基于以上腫瘤細胞的增長特點，利用下面兩種模型預測腫瘤數目或體積變化。

1.1 Malthus模型

設腫瘤時刻的體積為V(t)，初始時刻t0的體積為V0，單位時間內腫瘤的增長率為r(r為常數)，并且腫瘤的增長率與當時的體積成正比，則可以得到如下方程:

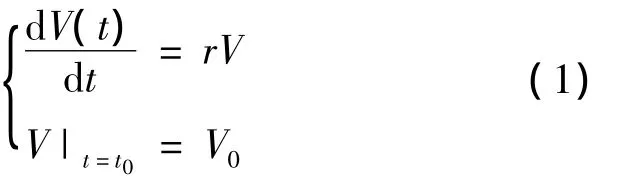
該方程的解為:

在臨床應用方面，腫瘤體積增大一倍所需要的時間是刻畫腫瘤生長的一個重要參數，記為σ，不難得到:

式(4)，(5)即為直徑的倍增公式。

令T=t－t0=kσ，k為倍增次數，取對數可得:

轉化為體積可得:

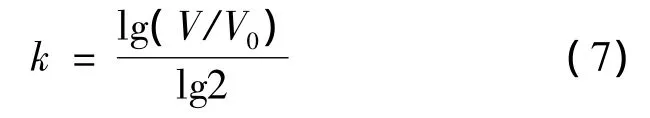
根據式(6)，可得一個直徑為10μm的癌細胞到臨床上能檢測出來直徑為1 cm的腫瘤細胞時需要分裂約30次，即k約為30。另外根據k的表達式，可以推導出此時的腫瘤細胞數量的函數表達式，假設初始時刻的腫瘤細胞的數量為N0，那么t時刻腫瘤細胞的數量就為:

可以檢測出來，細胞倍增30次的時候細胞數量大約是1011，代入式(8)可得N0=93。所以假定初始腫瘤細胞數為93，根據胃癌腫瘤細胞的倍增時間為90 d［6］，結合式(3)可知 r≈0.007 7。

1.2 Logistic模型

在Malthus模型的基礎上，我們考慮在腫瘤的增長過程中，由于營養供應有限，將會阻滯腫瘤細胞的增長速度，此時將模型修改為:

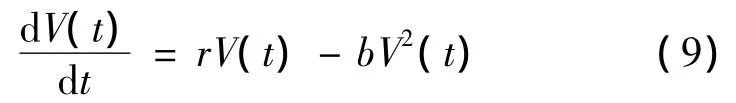
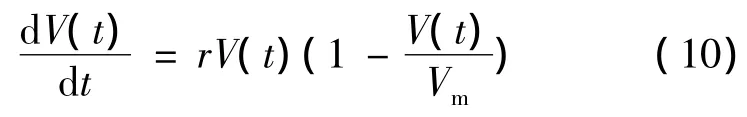
求解可得:

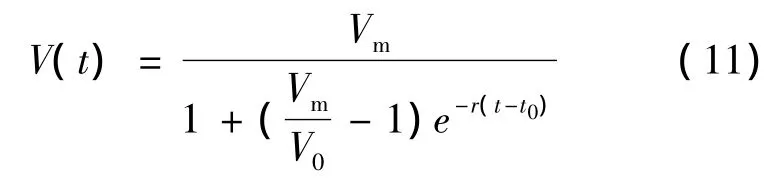
同理可推出:

其中，Dm為腫瘤細胞的最大直徑。此時可以得到腫瘤細胞的數量函數表達式是N=N0·2k。

2 結果

根據Malthus和Logistic模型，我們通過MATLAB編程，分別求出Malthus和Logistic模型的腫瘤細胞的生長模型和增長模型結果(見圖1－4)。

圖1 Malthus模型中直徑與時間的關系Figure 1 The diameter-time curve in Malthus model

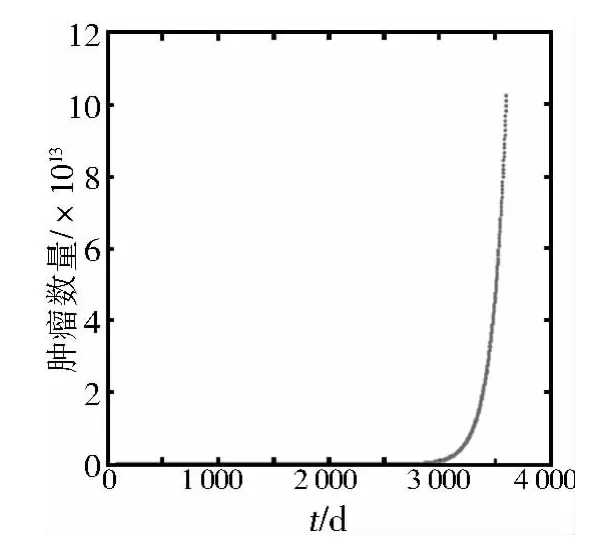
圖2 Malthus模型中數量與時間的關系Figure 2 The population-time curve in Malthus model

圖3 Logistic模型中直徑與時間的關系Figure 3 The diameter-time curve in Logistic model

對上面圖形進行分析，可以看出Malthus模型比Logistic模型的增長趨勢更大，在4 000 d后，Logistic模型趨于穩定，其趨于穩定的最大值 Vm，Nm，即腫瘤體積和數量的最大值，在Malthus模型沒有加入限制條件，假定環境無限，腫瘤細胞自由增長，所以曲線一直處于增長狀態，在Logistic模型中，加入環境限制，所以腫瘤數量只能趨于一個最大值，不可能無限制增長，直徑在1 700 d后就出現明顯上升趨勢，而數量卻在3 000 d后才出現顯著增長。從模型得出的數據可以看出在第30次倍增時，腫瘤細胞直徑為10.24 mm，數量為1011，此時的結果與實際相吻合，并且發現近期預測時，Malthus模型更適合;在中長期預測中Logistic模型更加合適。

圖4 Logistic模型中數量與時間的關系Figure 4 The population-time curve in Logistic model

3 討論

由于癌癥患者只能在倍增30次后才能檢測出患有癌癥，那就需要制定合理有效的方案使得病人盡早查出癌癥并花費最少。

由于腫瘤細胞在倍增到30次后才能被發現，并且在倍增到40次時就一定死亡，針對我們研究的胃癌，假設細胞倍增35次之后就是晚期，那么就需要在倍增35次之前就檢測出患有癌癥，胃癌的倍增時間是90 d，設每次檢查需要p元，要盡量使時間短和費用少，設腫瘤細胞從患者開始檢查的時候開始倍增，每次檢查間隔時間為d天，截止查出腫瘤細胞一共檢查了m次，在腫瘤細胞倍增30次后只要一次檢查就可以檢查出來是否患有癌癥，忽略儀器等的影響，這是雙目標問題，則可建立如下模型:

雙目標問題不好解決，此時加入權重，考慮到生命比金錢重要，取時間比例和費用分別為和，則模型可以簡化為:

若取p=3 000，通過Lingo編程，求解(14)式得出，即需要檢查4次，每次檢查間隔676d。

這一結果并不理想，只要檢查4次，每次檢查間隔676 d，接近于2年，這與實際不是很符合，于是，修改假設，將癌癥晚期設定為倍增33次，得m=6，d=451，將癌癥晚期設定為32次，得m=8，d=338，此時比較符合實際，建議癌癥患者每338d檢查一次，另外還可以修改權重比例。

綜上，本文針對腫瘤細胞的增長建立了Malthus模型和Logistic模型，對腫瘤的直徑生長和數量生長進行了建模，得出較為理想的結論。不過模型忽略了很多外界條件，有待于修正。針對檢查機制，我們建立了優化模型，將雙目標問題改為加權的單目標問題，對模型最后的加權比重和晚期癌癥時限進行取值討論，得出較為理想的結論，這也為臨床檢查提供了依據。

［1］姜啟源，謝金星，葉俊.數學模型［M］.3版.北京:高等教育出版社，2003:135－144.

［2］張學良.Malthus和Logistic模型及其醫學應用［J］.數理醫藥學雜志，2008，21(5):516－518.

［3］Domingues JS.Gompertz model:Resolution and analysis for tumors［J］.JMath Model Appl，2012，1(7):70－77.

［4］Norton L.A Gompertzian model of human breast cancer growth［J］.Cancer Res，1988，48:7067－7071.

［5］Mackenzie D.Mathematical modeling and cancer［J］.SIAM News，2004，37(1):1－3.

［6］Wu CW，Lo SS，Shen KH，etal.Incidence and factors associated with recurrence patterns after intended curative surgery for gastric cancer［J］.World JSurg，2003，27:153－158.