雙圈圖的無符號拉普拉斯特征多項式的系數

徐麗珍， 何常香

（上海理工大學 理學院，上海 200093）

1 基本定義

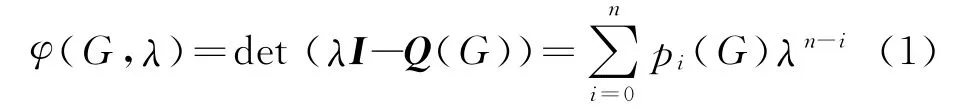
式中，I為n 階單位矩陣.

如果連通圖G 的邊數等于頂點數，則稱G 為單圈圖；如果連通圖G 的邊數等于頂點數加1，則稱G為雙圈圖.G－e表示由G 刪去邊e后得到的圖.

定義1［1］設H 是圖G 的一個生成子圖，若H的連通分支是樹，或者是圈長為奇數的單圈圖，則稱H 是圖G 的一個TU－子圖；若H 恰有c個圈長為奇數的單圈分支和s個樹分支T1，T2，…，Ts，則定義表示樹Ti的階數.

引理1［1］設Hi為圖G 中所有具有i 條邊的TU－子圖集合，則式（1）中p0（G）＝1，

在引理1中，由于Hi的確定比較困難，所以，pi（G）也很難被確定.文獻［1］給出了無符號拉普拉斯特征多項式系數p1（G）和p2（G）的表達式.文獻［2］給出了p3（G）的表達式.文獻［3］給出了經刪邊、剖分及移鄰等變換后所得圖G′的pi（G′）的絕對值與原圖pi（G）的絕對值的大小關系，并以此為工具，確定了無符號拉普拉斯特征多項式系數絕對值最小的單圈圖.更多關于系數的研究見文獻［4－9］.現主要研究雙圈圖的無符號拉普拉斯特征多項式的常數項.

2 雙圈圖的分類

設B（n）為所有n 階雙圈圖的集合，不含懸掛點的雙圈圖有B（r，s，l）和B（Pk，Pl，Pt）這兩類，如圖1所示.

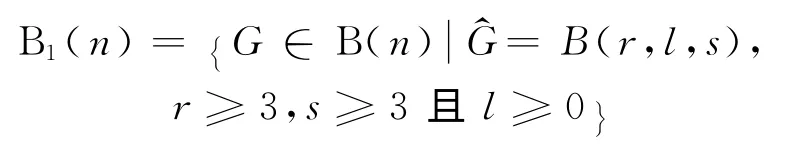
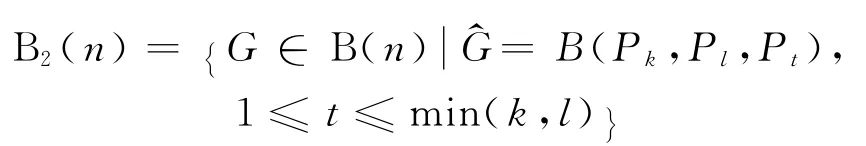
易見Bn（n）＝B1（n）∪B2（n）.

圖1 B（r，s，l）和B（Pk，Pl，Pt）Fig.1 B（r，s，l）and B（Pk，Pl，Pt）

3 雙圈圖的無符號拉普拉斯系數pn（G）

現主要給出兩類雙圈圖的無符號拉普拉斯特征多項式的常數項.

定義4 設圖G 是n 階連通圖，e＝v1v2是圖G的一條非懸掛邊，在圖G 中的點v1處添加一條懸掛邊，再將邊e收縮（即將點v1和v2粘合）后得到一個新的n階連通圖G′＝τ（G，1，2）.

定理1 設G∈B1（n），則

證明 由引理1可知

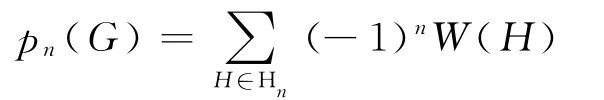
若H∈Hn，則H 為G 的邊數為n＋1－1＝n 的TU－子圖，即存在e∈E（G）使得H ＝G－e；若e?E（），則G－e?Hn.以下假設e∈E），按r，s的奇偶性進行討論.

情形1 若r，s均為偶數.

此時Hn＝φ，從而有pn（G）＝0.

情形2 若r，s的奇偶性不同.

不失一般性，不妨設x＝r 為偶數（即Cr為偶圈）.只有當e∈E（Cr）時，H＝G－e才是G 的TU－子圖，并且此時的W（H）＝4，從而有

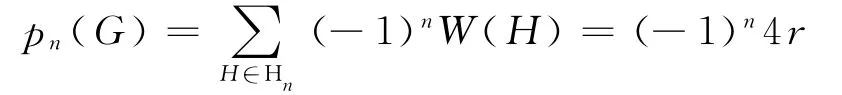
情形3 若r，s均為奇數.

若e不在圈上，則G－e是G 的含2個奇單圈分支的TU－子圖，故W（H）＝42；若e在圈上，則Ge是G 的恰有1個奇單圈分支的TU－子圖，且W（H）＝4.綜上

由定理1的結論可知，收縮加懸掛邊后雙圈圖中圈的奇偶性發生改變，所以，圖的無符號拉普拉斯特征多項式系數pn（G）的大小關系很難確定.

例1 設圖G 的階數為n＝9，圖G′和G″是由圖G 收縮邊v1v2加一條懸掛邊于點v1而得到的，如圖2和3所示.

圖2 圖G1和圖G′＝τ（G1，1，2）Fig.2 Graph G1and G′＝τ（G1，1，2）

圖3 圖G2和圖G″＝τ（G2，1，2）Fig3 Graph G2and G″＝τ（G2，1，2）

顯然pn（G1）＝pn（G2）＝－16，pn（G′）＝－（4×5＋4×3＋42×1）＝－48，pn（G″）＝0，pn（G1）≥pn（G′），pn（G2）≤pn（G″）.

定理2 設G∈B2（n），則

式中，x，y 為k，l，t中奇偶性相同的2個數.

證明 由引理1可知

若H∈Hn，則H 為G 的邊數為n＋1－1＝n 的TU－子圖，即存在e∈G 使得H ＝G－e；若e?，則G－e?Hn.以下假設e∈，按k，l，t的奇偶性進行討論.

情形1 若k，l，t這三者的奇偶性相同.

不失一般性，不妨假設k，l，t均為偶數，此時Hn＝φ，從而有pn（G）＝0.

情形2 若k，l，t這三者的奇偶性不完全相同.不妨設x＝l，y＝t為偶數，k為奇數.

若e在x 到y 的長為k 的路中，則G－e不是TU－子圖；若e在x 到y 的長為l或t的路中，則G－e是G 的恰有一個奇單圈分支的TU－子圖，故W（H）＝4.綜上

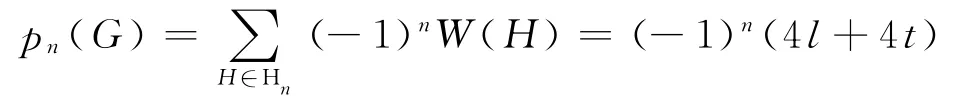
由定理1和定理2可知，對于非二部雙圈圖，pn（G）的絕對值有最小值16.由定理1和r≥3，s≥3可知，當r＝4或s＝4時，pn（G）的絕對值取到最小值16，即非二部雙圈圖的pn（G）的絕對值取到最小值16時，第一類雙圈圖B1（n）必含有1個C4圈和1個奇單圈；由定理2可知，當x＝1，y＝3或x＝2，y＝2時，pn（G）的絕對值取到最小值16，即非二部圖pn（G）的絕對值取到最小值16時，第二類雙圈圖B2（n）必含有1個C4圈和1個奇單圈.同時，由以上定理可知，雙圈圖的無符號拉普拉斯特征多項式的常數項只與圈長的奇偶性有關.

［1］Cvetkovi D，Rowlinson P，Simic S.Signless Laplacian of finite graphs［J］.Linear Algebra and its Applications，2007，423（1）：155－171.

［2］Wang J F，Huang Q H.Some results on the signless Laplacians of graphs［J］.Applied Mathematics Letters，2010，23（9）：1045－1049.

［3］Mirzakhah M，Kiani D.Some results on signless Laplacian coefficients of graphs［J］.Linear Algebra and its Applications，2012，437（9）：2243－2251.

［4］Oliveira C S，Maia de Abreu N M，Jurkiewicz S.The characteristic polynomial of the Laplacian of graphs in（a，b）－linear classes［J］.Linear Algebra and its Applications，2002，356（1／2／3）：113－121.

［5］He C X，Shan H Y.On the Laplacian coefficients of bicyclic graphs［J］.Discrete Mathematics，2010，310（23）：3404－3412.

［6］Mohar B.On the Laplacian coefficients of acyclic graphs［J］.Linear Algebra and its Applicatons，2007，422（2／3）：736－741.

［7］Ilic A，Ilic M.Laplacian coefficients of trees with given number of leaves or vertices of degree two［J］.Linear Algebra and its Applications，2009，431（11）：2195－2202.

［8］Stevanovic D，Ilic A.On the Laplacian coefcients of unicyclic graphs［J］.Linear Algebra and its Applications，2009，430（8／9）：2290－2300.

［9］陳永玲，何常香.二部雙圈圖的拉普拉斯系數［J］.上海理工大學學報，2012，34（5）：481－486.