被動電磁裝甲對金屬射流的電流作用特性

苑希超 雷 彬 李治源 陳少輝

（1.軍械工程學院彈藥工程系 石家莊 050003 2.北京航空工程技術研究中心 北京 100076）

1 引言

被動電磁裝甲的概念是由美國專家Walker[1]于1973 年首次提出的，具有結構簡單、成本低、重量輕、無附帶傷害及可提供全方位防護的優點。鑒于其巨大應用潛力和良好發展前景，被動電磁裝甲引起了廣泛的關注。但由于其理論涉及電磁學、熱學、塑性力學、磁流體動力學等學科；試驗技術上涉及聚能裝藥技術、脈沖功率技術、高壓絕緣技術、以及納秒級X 光照相等復雜技術。因而雖然國內外很多學者都對電磁裝甲進行了大量研究，但被動電磁裝甲的作用機理仍處于探索階段，至今尚無準確系統的理論分析方法。

被動電磁裝甲對金屬射流的作用機理非常復雜，但從根本上說是脈沖電流對金屬射流的作用。進行脈沖電流對金屬射流電流作用特性的研究，是完善被動電磁裝甲防護機理的基礎。國內外目前已有一些學者對被動電磁裝甲作用機理進行了研究[2-5]，但并沒有涉及到作用過程中存在的電流趨膚效應和高速運動的射流通過裝甲板時的作用時間問題，因此需要進一步研究。

關于趨膚效應的研究早在19 世紀便已經開始[6]。由于趨膚效應使電阻、電感隨著交流電頻率的增加而增加，導致電流傳輸的效率降低，所以，在頻率設計、微波線路、電力傳輸等方面都有大量學者開展相關研究[7-11]。關于趨膚效應的分析可以通過時域分析和頻域分析兩種方法進行。Edward 等人[12]將時域分析方法引入趨膚效應的計算；Yen 等人[13]根據趨膚效應微分方程提出了一種等效電路模型。但是根據Kim 和Neikirk[14]的研究，這種方法不能精確地計算高頻情況下的趨膚效應，并提出了一種梯形電路模型改進了Yen 等人的研究。趨膚效應頻域分析方法的研究也已經開展。Lawrence[15]對趨膚效應的時域分析和頻域分析方法做了總結。Gatous等人[16]采用頻率分析方法得到了不同頻率下導體電感和電阻的計算公式，并將其表示成關于頻率的函數，得到其隨頻率變化的規律。Ausserhofer 等人[17]采用定點計算技術從時域和頻域兩種方法求解了靜態電磁場的趨膚效應問題。隨著數值計算和有限元仿真技術的發展，也有很多學者對趨膚效應問題進行了數值仿真的研究[18-20]。但是，研究的重點依然在頻率變化對電阻、電感的影響，以及電流傳輸的效率上。目前鮮有針對脈沖電流的趨膚效應開展的研究。

本文提出一種基于頻域分析的脈沖電流趨膚效應分析方法，并以被動電磁裝甲的電路模型為背景，進行了脈沖電流分布的計算和仿真研究，同時，根據金屬射流的電流作用時間模型，對被動電磁裝甲對金屬射流電流作用特性進行了分析。

2 被動電磁裝甲模型

被動電磁裝甲主要由連接到高功率脈沖電源的兩塊間隔一定距離的薄金屬板組成，其原理如圖1所示。

在圖1 中，已充電的電容器組C 通過開關7 和導線連接到一對絕緣固定的平行金屬裝甲板4 和5上，主裝甲6 位于后裝甲板5 的后部；在開關7 閉合情況下，聚能裝藥1 爆炸使金屬射流3 從虛擬源點2 開始運動，在瞬間先后穿透電裝甲板4 和5 時，形成放電回路；電容器組C 隨即給回路放電形成強脈沖電流；脈沖電流對金屬射流產生力學、熱學、電磁學等方面的作用，從而降低金屬射流3 對主裝甲6 的侵徹深度。

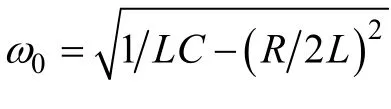
金屬射流速度一般處于2～8km/s 之間，因此金屬射流穿過間距為80mm 平行裝甲板所需時間大約為60μs。所以，實際流過射流的電流波形只是電容器放電波形的一部分。

根據已有的研究[3]，取電容C=1.2mF，系統電阻R=15mΩ，電感L=1μH，充電電壓U0=18kV，作用時間T=60μs。可以得到實際作用在金屬射流上的電流波形，該波形呈現明顯的脈沖特性。此時，典型的單一頻率的趨膚深度和趨膚效應的分析方法并不適適用。需要針對脈沖電流的特點，尋找一種可以適用于任何情況的趨膚效應分析方法。

3 脈沖電流的頻域分析

雖然式（1）中電流存在震蕩角頻率ω0，但是由于信號存在指數衰減，并且由于電流對金屬射流的實際作用時間很短，對電流信號進行了截短。因此，金屬射流中的電流絕不是單一的頻率，必然存在更為復雜的頻率成分。為進一步分析脈沖電流的密度分布，將實際作用的電流進行傅里葉變換。

式中，0 和T 分別為電流作用的起始和結束時刻，積分后的表達式I～是時間的函數，表示為

由ω=2πf進行換算可得到頻域分布 I (f)，對頻域分布進行傅里葉反變換，時域電流函數可表達為

此時，頻率為f 的電流分量可表示為

采用上節所設定的電路參數值，得到金屬射流上的電流的頻譜如圖2 所示。

圖2 金屬射流上的電流的頻譜Fig.2 Frequency spectrum of the current

由圖中可以看出，射流上的電流具有很寬的頻率分布，在0～50kHz 的頻帶內具有較大的振幅。所以，金屬射流上的總電流可以看作是不同頻率的交變電流的加權疊加。

4 脈沖電流密度計算

針對上節關于脈沖電流頻率分布的分析，考慮將脈沖電流分解成不同頻率的時諧電流進行分析，通過不同頻率成分的電流分布的疊加，得到脈沖電流總體的電流密度分布。

為簡化計算，選擇圓柱坐標系（z，r，θ）作為參考坐標系，并做以下假設:

（1）金屬射流軸向和徑向速度為零，且無旋轉。

（2）金屬射流長度明顯大于其半徑，磁感應強度和電流密度的端部效應可忽略。

（3）金屬射流中電場強度及電流密度只有z 方向分量，磁感應強度只有θ 方向的分量。

（4）金屬射流為紫銅金屬導體，其位移電流密度與傳導電流密度相比很小。因此其中的位移電流可忽略不計。

根據上面的假設，可以采用圓柱形銅導體來模擬靜態直射流，如圖3 所示。導體直徑r0，陰影部分為導體橫截面，由于其軸對稱性，可以采用其橫截面進行二維分析來進一步簡化計算。對于頻率為f 的正弦交變電流，根據上面的假設，麥克斯韋方程組在金屬射流內部可簡化為以下形式:

式中，μ0是真空磁導率；r 為徑向位置的坐標。

圖3 圓柱導體模型Fig.3 Cylindrical conductor model

其截面上電流密度分布表示為

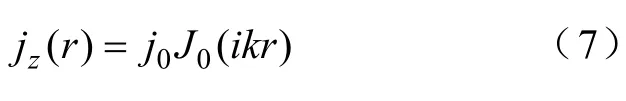
由上節得到，脈沖電流中頻率為f 的電流分量為I (f,t)=I (f)ej2πft，對式（7）式進行面積分，得到同一頻率時總電流的表達式

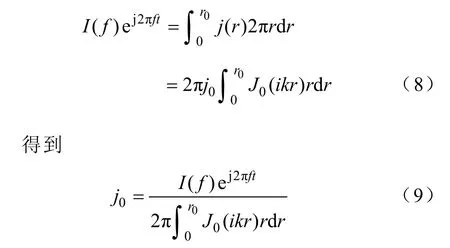
對式（7）式進行頻率的積分，得到所有頻率疊加后電流密度的分布

5 仿真計算與結果分析

5.1 電流密度計算與趨膚效應分析

選用第2 節中的電路參數，對半徑2mm 的銅導線內的電流密度分布進行了數值計算。此時放電總電流波形和頻率分布分別如圖2 和圖3 所示。通過對式（10）的求解，得到不同時刻時金屬射流內電流密度分布，如圖4 所示。

圖4 采用頻域分析方法得到的電流密度分布Fig.4 Current density distribution from frequency-domain analysis method

同樣參數情況下采用有限元軟件Ansoft 進行了瞬態二維場仿真，得到計算結果。圖5 給出了60μs時電流密度的矢量圖，從圖中可以看出，其表面的電流密度并不是最大，與頻域分析的結果相符。同時，圖6 給出了頻域分析方法和有限元方法的計算誤差。

圖5 有限元方法得到的電流密度分布Fig.5 Current density distribution from FEM method

圖6 計算誤差分布Fig.6 Calculation error distribution

通過圖6 可已看出，計算結果的最大誤差為3×109A/m2左右，而對比圖4 可以得到，此時的相對誤差僅為6%，從而證明了所提方法的有效性。

進一步分析脈沖電流密度分布的計算結果，可以看出，不同時刻電流密度分布的規律并不固定，而是隨著時間不斷變化的。在放電初期，電流密度隨著深度的增加而減少，但是在后期出現了表面電流密度小于內部電流密度的現象。為更加清楚的表現不同時刻電流密度分布的變化，采用下式進行歸一化

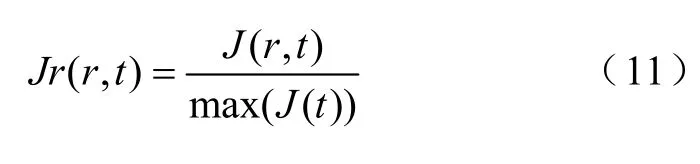
式中，Jr (r,t) 表示t 時刻距離中心r 處的相對電流密度；max(J (t)) 表示t 時刻半徑方向上的電流密度J (t)的最大值。

相對密度的分布如圖7 所示。

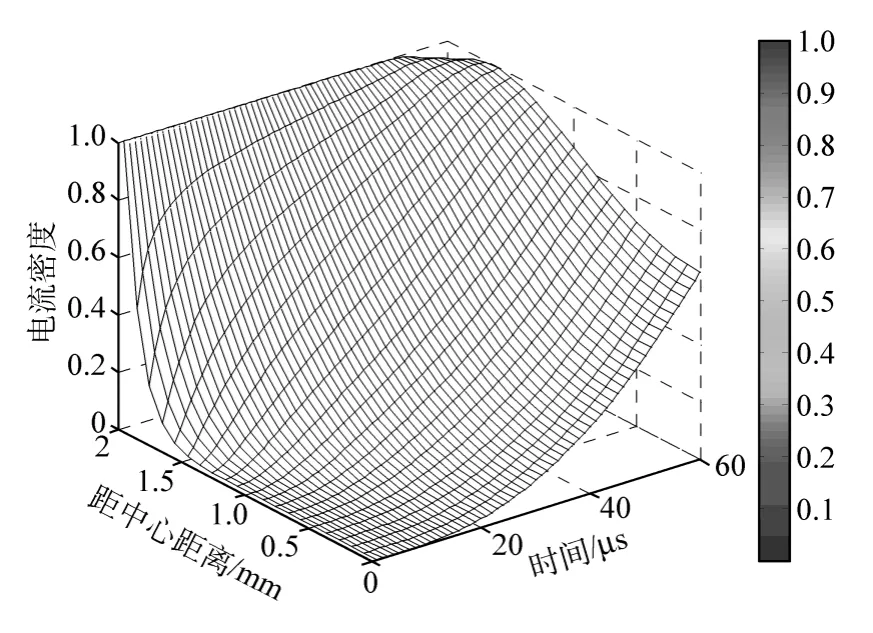
圖7 相對電流密度分布Fig.7 Relative current density distribution

從圖7 可以看出，相對電流密度的最大值并不是一直在表面處，而且電流密度下降的速度也在隨時間變化。

為更加直觀地進行對比，圖8 分別給出了15μs、30μs、45μs 和60μs 時半徑方向上的電流密度分布曲線。從圖8 可以看出，放電開始階段，電流密度隨著深度的增加而劇烈地減小，而隨著時間的增加，這種減小的速度逐漸緩慢，而到了60μs 時，變化趨勢更加緩慢，而且出現了內部電流密度大于表面電流密度的現象。

若定義趨膚深度為電流密度降為表面電流密度的1/e 時的深度，即j (r0-δ)=j (r0)e 。那么，得到電流趨膚深度隨時間變化的規律如圖9 所示。可以看出，趨膚深度并非固定不變的，而是隨著時間的增長而增加。

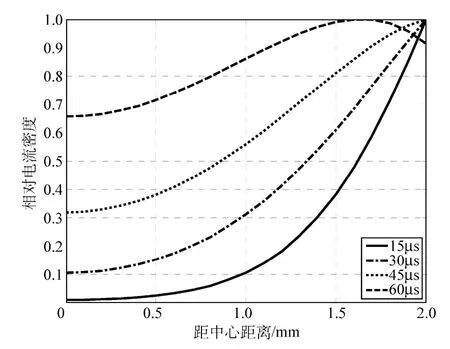
圖8 不同時刻電流密度分布曲線Fig.8 Current density distribution curve at different time

圖9 不同時刻電流趨膚深度變化Fig.9 Skin depth variation at different time

5.2 電流比作用量分析

電流在金屬射流上的能量積累可以用比作用量進行表示。通常定義比作用量為

式中，J 表示金屬射流中的電流密度；t1和t2分別表示電流作用的起始和結束時間。

結合虛擬源點理論[21]，可以求解射流微元所受電流作用的比作用量值。令vtip和vtail分別表示射流頭部和尾部的運動速度。任取射流上一速度為vj的微元，根據圖1 中的幾何關系，得到開始放電的時刻 t0=(S0+d0)/vtip。那么

式中，S0為虛擬源點O 到前裝甲板的距離；d0為兩平行裝甲板間距；t1和t2分別表示電流對微元作用的起始和結束時間。

圖10a 和圖10b 分別為半徑1mm 和半徑2mm的射流微元受到的電流比作用量的分布，從圖中顯示，比作用量在速度方向上變化十分明顯，從而可以看出在半徑方向，由于存在趨膚效應，所以靠近射流表面處的電流作用能量高于射流中心處，半徑越大的射流這種趨勢越明顯。在速度方向，電流對射流作用的能量主要集中在速度小于4km/s 的射流尾部，對射流頭部作用很小。結合前面的研究，分析其原因可能為:一是射流頭部速度高，該部分微元穿過裝甲板的持續時間斷，二是受到放電電流上升速度的影響，射流頭部穿過裝甲板時，系統放電電流幅值較小。

圖10 射流微元所受比作用量的分布Fig.10 Distribution of action ratio in shaped charge jet element

但是，射流頭部因為速度較高，對裝甲具有更強的破壞作用，因此，優化裝甲板間距和電路參數是進一步提高被動電磁裝甲防護性能的一個研究方向。而本文的分析方法為其提供了研究基礎。

6 結論

本文以被動電磁裝甲為應用背景，提出了一種脈沖電流趨膚效應的頻域分析方法，并分析了電流對射流作用的特性。得到以下結論:

（1）提出一種脈沖電流密度分布的頻域計算方法，得到金屬射流模型中脈沖電流密度分布的計算公式，采用數值計算方法對電流密度進行了求解，通過與有限元方法的比較，驗證了該頻域分析方法的正確性。

（2）通過對脈沖電流密度分布的計算，分析了電流密度分布隨時間的變化規律，結果表明，并非所有時刻電流密度都隨深度增加而減小。在脈沖下降沿會出現表面的電流密度小于內部電流密度的現象。

（3）通過等效的趨膚深度的求解與分析，得到脈沖電流作用下金屬射流內趨膚深度的變化規律，結果表明，趨膚深度并非固定值，而是隨著時間的增加而增大。

（4）通過比作用量的分析，可以看出電流作用的主要的能量集中在射流尾部，而對射流頭部的作用較小。從而為電磁裝甲進一步優化提供了研究基礎。

[1]Walker E H.Defeat of shaped-charge devices by active armor[R].Aberdeen Proving Ground,MD:U.S.Army Ballistic Research Laboratory,1973.

[2]雷彬,陳少輝,呂慶敖,等.被動電磁裝甲對金屬射流橫向電磁力的計算及驗證[J].高電壓技術,2011,37(10):2569-2574.Lei Bin,Chen Shaohui,Lü Qingao,et al.Calculation and verification of lateral electromagnetic force on the shaped charge jet in the passive electromagnetic armor[J].High Voltage Engineering,2011,37(10):2569-2574.

[3]苑希超,雷彬,李治源,等.被動電磁裝甲對金屬射流箍縮電磁力的計算及驗證[J].高電壓技術,2013,39(1):251-256.Yuan Xichao,Lei Bin,Li Zhiyuan,et al.Calculation and verification of pinch electromagnetic action on the shaped charge jet in the passive electromagnetic armor[J].High Voltage Engineering,2013,39(1):251-256.

[4]Wickert M.Electric armor against shaped charges:Analysis of jet distortion with respect to jet dynamics and current flow[J].IEEE Transactions on Magnetics,2007,43(1):426-429.

[5]Appelgren P,Larsson A,Lundberg P,et al.Studies of electrically-exploded conductors for electric armour applications[C].2nd Euro-Asian Pulsed Power Conference Vilnius,Lithuania,2008:1072-1074.

[6]Simonyi K.Foundations of electrical engineering[M].New York:Macmillan,1963.

[7]喻樂,和敬涵,王小君,等.基于階躍級數逼近法的城市軌道交通鋼軌短路電流趨膚效應研究[J].電工技術學報,2012,27(4):7-12.Yu Le,He Jinghan,Wang Xiaojun,et al.Research of short-circuit skin effect current of DC railway based on step series algorithm[J].Transactions of China Electrotechnical Society,2012,27(4):7-12.

[8]江壯賢,莊勁武,王晨,等.基于電磁斥力原理的高速觸頭機構仿真分析與設計[J].電工技術學報,2011,26(8):172-177.Jiang Zhuangxian,Zhuang Jinwu,Wang Chen,et al.Simulation analysis and design of a high speed contact mechanism based on electro-magnetic repulsion mechanism[J].Transactions of China Electrotechnical Society,2011,26(8):172-177.

[9]鄭雪,樂健,蔡偉,等.電力線載波通信元件阻抗模型研究綜述[J].電力系統保護與控制,2012,40(6):135-141.Zheng Xue,Le Jian,Cai Wei,et al.Overview of the component impedance modeling research of power line communication[J].Power System Protection and Control,2012,40(6):135-141.

[10]張皓嵐,賀慧英,陳濤,等.艦船電力載波通信的阻抗匹配設計[J].電力系統保護與控制,2014,42(2):104-110.Zhang Haolan,He Huiying,Chen Tao,et al.Impedance matching research on power line carrier applied to shipboard electric network[J].Power System Protection and Control,2014,42(2):104-110.

[11]喻樂,和敬涵,王小君,等.基于Mexh 小波變換的直流饋線保護方法[J].電力系統保護與控制,2012,40(11):42-45,54.Yu Le,He Jinghan,Wang Xiaojun,et al.DC feeder protection based on Mexh wavelet[J].Power System Protection and Control,2012,40(11):42-45,54.

[12]Edward J T,Thomas T H,Pfullerton H.Transientresistance of conductors[J].IEEE Transactions on Power Apparatus and Systems,1968,87(2):455-462.

[13]Yen C S,Fazarin Z,Wheeler R L.Time-domain skineffect model for transient analysis of lossy transmission lines[J].Proc.IEEE,1982,70(7):750-757.

[14]Kim S,Neikirk D P.Compact equivalent circuit model for the skin effect[C].IEEE MTT2S International Microwave Symposium Digest,San Franscisco,1996:1815-1818.

[15]Lawrence J G.Frequency-and time-domain analysis of skin effects[J].IEEE Transactions on Magnetics,1996,32(1):220-229.

[16]Gatous O M O,Pissolato J.Frequency-dependent skin-effect formulation for resistance and internal inductance of a solid cylindrical conductor[J].IEE Pro.Microw Antennas Propag,2004,151(3):212-216.

[17]Ausserhofer S,Biro O,Preis K.Frequency and time domain analysis of nonlinear periodic electromagnetic problems[C].International Conference on Electromagnetics in Advanced Applications,Torino,Italy,2007.

[18]Bíró O,B?hm P,Preis K,et al.Edge finite elements analysis of transient skin effect problems[J].IEEE Transactions on Magnetics,2000,36(4):835-839.

[19]Kim H K,Jung J K,Park K Y,et al.Efficient technique for 3-D finite element analysis of skin effect in current-carrying conduction[J].IEEE Transactions on Magnetics,2004,40(2):1326-1329.

[20]劉素貞,張闖,金亮,等.電磁超聲換能器的三維有限元分析[J].電工技術學報,2013,28(8):7-12.Liu Suzhen,Zhang Chuang,Jin Liang,et al.3D finite element analysis of electromagnetic ultrasonic transducers[J].Transactions of China Electrotechnical Society,2013,28(8):7-12.

[21]Allison F E,Vitali R A.A new method of computing penetration variables for shaped-charge jets[R].Maryland:Ballistic Research Laboratory,1963.