計及定子開槽的插入式永磁電機轉子偏心空載氣隙磁場全局解析迭代模型

周曉燕 章躍進 李 琛 仇志堅

（1.青島理工大學自動化工程學院 青島 266033 2.上海大學機電工程與自動化學院 上海 200072）

1 引言

本文研究的插入式永磁電機定轉子開槽，轉子上的永磁體沉入轉子槽內，且極性相同。相鄰永磁體之間為鐵心凸極，在永磁體的磁化作用下，呈現出與永磁體相反的極性，從而構成鐵極與永磁極交替出現的結構。研究表明此種電機結構具有懸浮和旋轉自解耦的優良屬性[1-8]。但是該結構使得這種電機氣隙磁場的分布更為復雜，尤其增加了轉子偏心氣隙磁場的計算難度。

目前插入式永磁電機電磁場計算的研究主要采用有限元法[4-8]，有限元法計算精度高，但在偏心量發生變化后，必須重新剖分，使用不夠方便；并且計算過程中需要良好的網格剖分保證其高計算精度；有限元法計算偏心力，一般采用虛位移法和麥克斯韋張量法。虛位移法計算比較繁瑣；而麥克斯韋張量法計算偏心力時，氣隙中的線積分路徑需穿過許多有限元網格，網格的品質及從何處穿過網格單元都會對計算結果產生影響[9,10]。較之有限元法，解析法參數調整方便，能快速計算不同轉子位置下的氣隙磁場，解析表達式能直接反映磁場分布與各參數之間的關系，并且避免了計算偏心力時有限元法在剖分網格和曲面位置選擇上的不足。

目前，攝動法在表貼式永磁電機偏心磁場解析分析中取得了較好效果[11-14]。攝動法又稱小參數展開法。選擇一個能反映物理特征的無量綱小參數作為攝動量（這里為偏心率），然后假設解可以按小參數展開成冪級數，將這一形式級數代入無量綱方程后，可得各級近似方程，依據這些方程可確定冪級數的系數，對級數進行截斷近似，便得到原方程的漸進解。文獻[11]應用攝動法求解忽略定子槽影響的表貼式永磁電機偏心電磁場問題，文獻[12-14]提出了考慮定子槽影響的表貼式永磁電機氣隙磁場解決方案，以上電機由于永磁體貼在轉子表面，僅有定子開槽，故其偏心解析計算相對簡單，而插入式永磁電機由于永磁體沉入轉子槽內，故需要考慮定子和轉子兩方面開槽的影響，因此其解析計算模型比較復雜，求解困難。

本文利用解析迭代法研究定子開槽插入式永磁電機轉子偏心氣隙磁場分布，電機模型如圖1 所示，4 塊N 極充磁的永磁體沉入轉子槽內，模型分成3個區域:氣隙，永磁體和定子槽，Rs、Rr分別為定子內徑、轉子外徑，Rsy為定子槽底半徑，Rm為永磁體半徑，氣隙g=Rs-Rr，a 為永磁體寬度角，永磁體厚度hm=Rr-Rm，β為定子槽寬度角。本文分別經過以下三步求解該交替極電機的全局解析模型:①假設定子表面光滑，求解域分為永磁體和非均勻氣隙兩部分，應用攝動法計算轉子偏心情況下的氣隙磁場分布:將矢量磁位用攝動級數表示，并取級數的前兩項零階和一階近似，結合零階和一階邊界條件，得到此時的氣隙磁場分布；②求解域為定子槽和局部氣隙區域，利用以上的計算結果確定邊界條件，得到考慮定子開槽影響的磁場分布；③獲得定子開槽后的邊界條件，再次計算。經多次迭代，得到最終解。

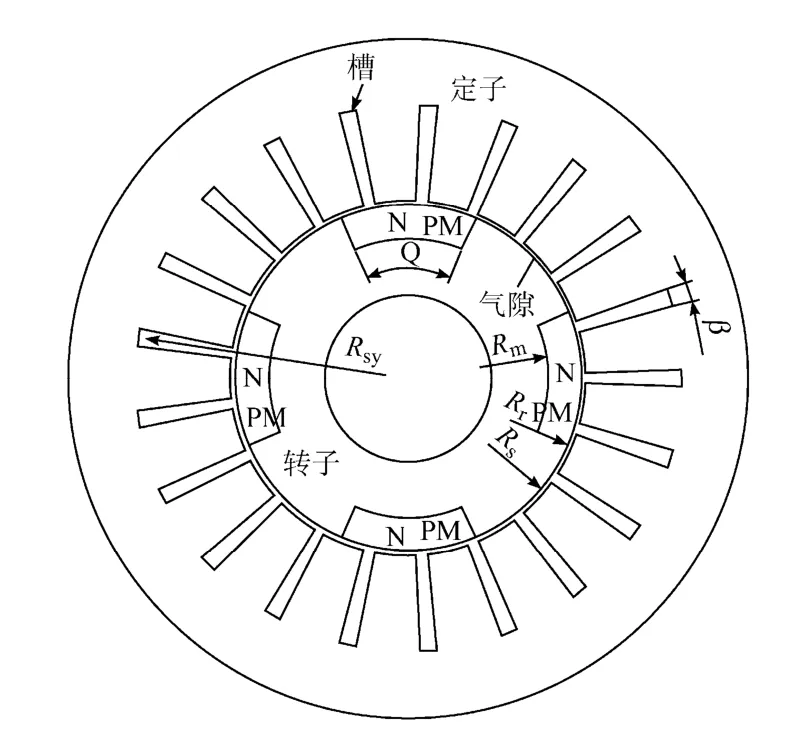
圖1 插入式永磁電機全局模型Fig.1 Insert permanent magnet global model

2 定子無槽、轉子偏心氣隙磁場模型

2.1 模型

圖2 所示為該電機定子無槽、轉子偏心模型。求解區域分成非均勻氣隙區域和永磁體區域兩部分。其中轉子軸心為Or，定子軸心為Os。d 為轉子和定子軸心的偏心距離，φ 為Os和Or的連線與極軸的夾角，即偏心角。轉子軸心為坐標原點，偏心率定義為

式中 Rs——定子內半徑。

圖2 定子無槽、轉子偏心模型Fig.2 Insert permanent magnet with rotor eccentricity and slotless

為簡化計算，對模型做如下假設:①轉動過程中定轉子軸心保持平行；②定轉子鐵心磁導率無窮大；③忽略渦流和飽和效應；④永磁體相對磁導率μr=1。

2.2 偏微分方程和邊界條件

在極坐標系下，氣隙區域和永磁體區域矢量磁位拉普拉斯方程和泊松方程如下:

其中，永磁體磁化如圖3 所示，對磁化強度M進行傅里葉分解[16]，得

Br——永磁體剩磁；

p——極對數；

μ0——空氣磁導率；

j——第j 塊永磁體；

m——永磁體區域的諧波次數；

a——永磁體寬度角。

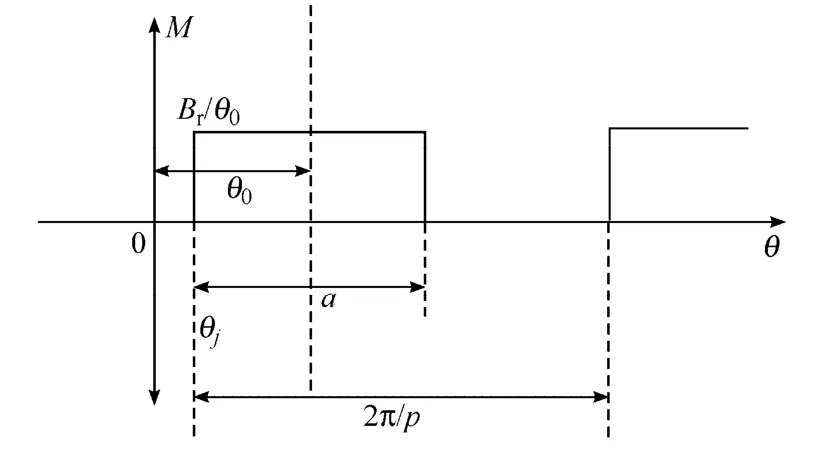
圖3 永磁體充磁Fig.3 Radial magnetization

兩個區域磁通密度和磁場強度的關系為[17]

在極坐標系下，磁場強度表達式為[17]

式中，i=1 表示氣隙域，i=2 表示永磁體域。

定子與氣隙交界面邊界條件描述為[11]

式中 n——邊界上的單位法向矢量。

根據攝動法，極坐標系下定子內徑圓軌跡為[15]

在圖2 所示坐標系下，可以表示為[11]

因此，定子內圓邊界可以表示為

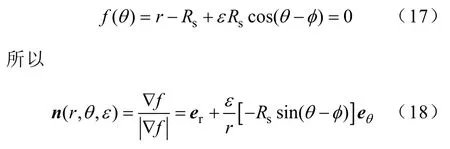
經過矢量運算，定子內徑邊界條件可以寫成

其他邊界如下:

式中 θj——第j 塊永磁體位置。

根據攝動理論，矢量磁位A 可以寫為

將式（26）和式（27）代入邊界式（19）中，并應用泰勒級數在Rs處展開得

將式（25）代入式（2）、式（3）中得到零階矢量磁位A 的偏微分方程如下:

將式（29）、式（30）代入邊界式（20）～式（24）中，可得零階邊界條件為

同理可得一階偏微分方程和邊界條件如下:

分別求解零階方程組式（29）～式（35）和一階方程組式（36）～式（42）即可得零階和一階解。

2.3 求解零階方程組

根據式（29）～式（35），氣隙區域和第j 塊永磁體區域的零階通解可以寫為[16]

最后，可以得到氣隙區域零階磁通密度分別為

2.4 求解一階方程

根據方程式（36）～式（42），氣隙和永磁體區域的一階矢量磁位A 的通解可寫成

將式（45）、式（46）和式（49）、式（50）代入攝動方程中，得到考慮轉子偏心氣隙磁通密度和氣隙磁位分布如下:

3 定子開槽模型

建立如圖4 所示模型，定子圓心為坐標原點，轉子坐標和定子坐標關系如下[11]:

圖4 定子開槽模型Fig.4 model with stator slot

模型分為兩個區域:氣隙和定子槽，分別建立氣隙和第h 個槽拉普拉斯方程為

氣隙通解為

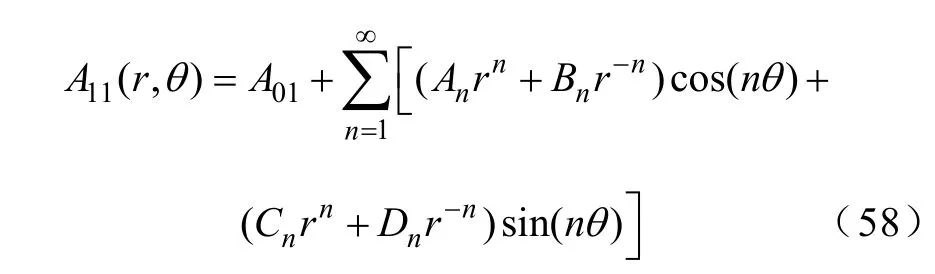
第h 個槽通解為[16]

式中 k——槽區域諧波次數。

取氣隙中半徑Rg，其磁位值作為開槽模型的邊界條件為

其他邊界條件為

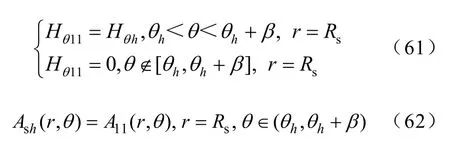
4 迭代修正

取定子開槽模型中氣隙圓周Rg1上的磁位值，作為圖5 所示模型的邊界條件，模型的方程、通解和其他邊界條件見式（29）、式（30）、式（32）～式（35）和式（43）、式（44），可以得到此時的氣隙磁位分布，將此磁位值作為定子開槽模型的邊界條件，重復進行式（56）～式（62），如此迭代反復，設前后兩次計算結果的誤差為

式中 nn——氣隙域圓周上的計算磁位點數；

圖5 迭代模型Fig.5 Iteration model

考慮工程允許范圍，本文取δ=3%，視為迭代結束，此時可得最終氣隙磁場分布。

根據氣隙磁場分布可以得到偏心力和轉矩[17]為

式中 Lef——電機鐵心長。

5 與有限元分析結果比較

為檢驗插入式永磁電機轉子偏心氣隙磁場全局解析模型的準確性，本文使用Ansoft 有限元分析軟件，對一臺4 對極21 槽插入式永磁電機[7]二維建模，采用分數槽是為了增加極槽數的最小公倍數，抑制雙邊開槽結構的齒槽定位轉矩。將有限元分析結果與解析計算結果的磁通密度波形和偏心力作比較。電機模型參數見表1。

圖6 為d=0.08mm 時氣隙磁通密度解析結果和有限元計算結果的對比。由圖可知，氣隙磁通密度的解析結果與有限元分析結果相吻合，驗證了解析模型計算氣隙磁通密度的準確性。圖7 為d=0.16mm時氣隙磁通密度解析結果和有限元計算結果的對比。同樣，解析結果逼近有限元分析結果。

表1 電機模型參數Tab.1 Parameters of the motor model

圖6 氣隙磁通密度比較（d=0.08mm）Fig.6 FEM and analytical predicted flux density waveforms（d=0.08mm）

圖7 氣隙磁通密度比較（d=0.16mm）Fig.7 FEM and analytical predicted flux density waveforms（d=0.16mm）

不同偏心距離情況下偏心力解析結果和有限元分析結果及其相對誤差見表2。比較結果表明:偏心力的解析結果與有限元分析結果的相對誤差在4%以內，表明本文提出的插入式永磁電機轉子偏心全局解析模型在計算偏心力時的準確度。

表2 偏心力解析解與有限元解比較Tab.2 The eccentricity force

圖8 和圖9 分別為偏心距離d=0 和d=0.16mm時齒槽轉矩的解析解波形和有限元波形的比較結果。該電機在不偏心情況下齒槽轉矩幅值為±0.128N·m，在偏心距離為0.16mm 時齒槽轉矩幅值為+0.138N·m 和-0.186N·m，兩種偏心情況下解析結果逼近有限元結果。

圖8 齒槽轉矩比較（d=0）Fig.8 FEM and analytical predicted cogging torque（d=0）

圖9 齒槽轉矩比較（d=0.16mm）Fig.9 FEM and analytical predicted cogging torque（d=0.16mm）

6 結論

本文建立了插入式永磁電機轉子偏心全局解析迭代模型，忽略飽和作用，采用攝動方法推導并得到了定子無槽轉子偏心氣隙磁場分布，并用解析迭代法考慮定子開槽的影響。氣隙磁通密度和齒槽轉矩的解析結果與有限元分析結果相吻合，計算偏心力的相對誤差在4%之內，比較結果證明了該電機轉子偏心全局解析模型的正確性和有效性。該模型參數修改方便，能夠方便地計算各種轉子位置和偏心參數情況下電機的磁場分布。

附錄 A

將式（43）代入式（38）的右邊并應用泰勒級數展開，與方程左邊比較可得

將式（48）代入式（39）中得

對邊界式（40）、式（41）應用傅里葉級數展開可得

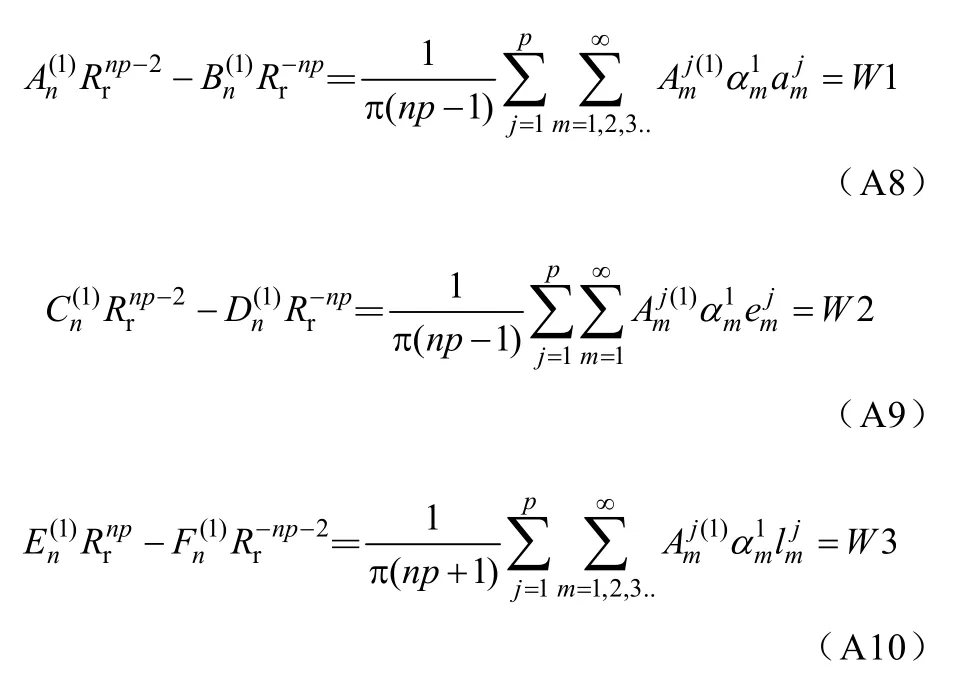
對永磁體邊界式（42）應用傅里葉級數展開得

附錄 B

將式（53）、式（58）代入邊界式（60）中，并應用傅里葉級數得

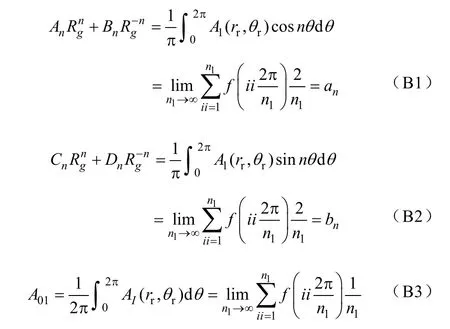
將式（58）、式（59）代入邊界式（61）中，應用傅里葉級數得

將式（58）、式（59）代入邊界式（62）中，對每槽積分得

根據式（B1）～式（B5）可以得到系數An-Dn的表達式為

[1]Dorrell D G,Amemiya J,Chiba A,et al.Analytical modeling of a consequent-pole bearingless permanent magnet motor[C].In Proc.IEEE Power Electronics and Electric Drives Conference,Singapore,2003:247-252.

[2]Amemiya J,Chiba A,Dorrell D G,et al.Basic characteristics of a consequent-pole type bearingless motor[J].IEEE Transactions on Magnetics,2005,41(1):82-89.

[3]仇志堅,鄧智泉,王曉琳,等.新型交替極無軸承永磁電機的原理與實現[J].中國電機工程學報,2007,27(33):1-5.Qiu Zhijian,Deng Zhiquan,Wang Xiaolin,et al.The principle and implementation of a new-type consequentpole bearingless permanent magnet motor[J].Proceedings of the CSEE,2007,27(33):1-5.

[4]Takenaga T,Kubota Y,Chiba A,et al.A principle and a design of a consequent-pole bearingless motor[C].In Proc.8th Int.Symp.Magnetic Bearings,Mito,Japan,2002:259-264.

[5]Takenaga T,Kubota Y,Chiba A,et al.A principle and winding design of consequent-pole bearingless motors[J].JSME International Journal Series,2003,46(2):363-369.

[6]Asami K,Chiba A,Rahman M A,et al.Stiffness analysis of a magnetically suspended bearingless motor with permanent magnet passive positioning[J].IEEE Transactions on Magnetics,2005,41(10):3820-3822.

[7]仇志堅.永磁型無軸承電機的基礎研究[D].南京:南京航空航天大學,2009.

[8]廖啟新,鄧智泉,王曉琳,等.交替極無軸承永磁電機的懸浮力脈動分析[J].中國電機工程學報,2007,27(30):49-54.Liao Qixin,Deng Zhiquan,Wang Xiaolin,et al.Suspension force pulse analysis of consequent-pole bearingless PM motor[J].Proceedings of the CSEE,2007,27(30):49-54.

[9]王興華,勵慶孚,王曙鴻.永磁無刷直流電機負載磁場及其電磁轉矩的計算[J].中國電機工程學報,2003,23(4):140-144.Wang Xinghua,Li Qingfu,Wang Shuhong.Analytical calculation of loaded magnetic field and electrical magnetic torque in brushless DC motor[J].Proceedings of the CSEE,2003,23(4):140-144.

[10]章躍進,江建中,屠關鎮.應用數值解析結合法計算旋轉電機磁場[J].電工技術學報,2004,19(1):7-11.Zhang Yuejin,Jiang Jianzhong,Tu Guanzhen.Application of numerical-analytical method to magnetic field computation in rotating electric machines[J].Transactions of China Electrotechnical Society,2004,19(1):7-11.

[11]Kim U,Lieu D K.Magnetic field calculation in permanent magnet motors with rotor eccentricity:without slotting effect[J].IEEE Transactions on Magnetics,1998,34(4):2243-2252.

[12]Kim U,Lieu D K.Magnetic field calculation in permanent magnet motors with rotor eccentricity:with slotting effect considered[J].IEEE Transactions on Magnetics,1998,34(4):2253-2266.

[13]Rahideh A,Korakianitis T.Analytical open-circuit magnetic field distribution of slotless brushless permanent-magnet machines with rotor eccentricity[J].IEEE Transactions on Magnetics,2011,47(12):4791-4808.

[14]Fu Jiajing,Zhu Changsheng.Subdomain model for predicting magnetic field in slotted surface mounted permanent-magnet machines with rotor eccentricity[J].IEEE Transactions on Magnetics,2012,48(5):1906-1917.

[15]Fu Werrbin,He Huan,Chen Zhongkuan.Mode analyses of quasi-rectangular waveguides by using PMOBG[J].Journal of Jishou University (Natural Science Edition),2003,24(4):43-47.

[16]李琛,章躍進,仇志堅.無軸承交替極永磁電機空載氣隙磁場全局解析模型[J].電工技術學報,2012,27(11):104-110.Li Chen,Zhang Yuejin,Qiu Zhijian.Exact analytical model for the no-load air-gap magnetic field calculation in consequent-pole permanent magnet bearingless motor[J].Transactions of China Electrotechnical Society,2012,27(11):104-110.

[17]湯蘊璆.電機內的電磁場[M].北京:科學出版社,1998.