基于變系數電感模型開關磁阻電機四象限無位置傳感器技術

蒯松巖 王鵬飛 成靜紅 譚國俊 劉送永

（1.中國礦業大學信息與電氣工程學院 徐州 221008 2.江蘇省電力傳動與自動控制工程技術研究中心 徐州 221116）

1 引言

開關磁阻電機具有結構簡單牢固，效率高，調速范圍廣，起動轉矩大等優點[1]，然而準確獲得轉子位置信息是開關磁阻電機（Switched Reluctance Motor,SRM）可靠運行和高性能控制的前提，位置傳感器的引入，不僅使電機結構的變得復雜，電機成本提高，而且也降低了電機運行的魯棒性與可靠性，限制了開關磁阻電機推廣和普及。因此，開關磁阻電機無位置傳感器技術具有較高的研究價值[2,3]。

在近幾年，開關磁阻電機無位置傳感器技術研究引起了國內外的廣泛關注，先后提出了一系列位置估計和無位置傳感器控制方案。這些方案大都采用測量、監視SR 電動機一相或幾相繞組的電流和磁鏈或者電流來推斷轉子的瞬時位置。文獻[4-6]采用磁鏈-電流法，基于SRM 磁鏈特性通過實現檢測相繞組磁鏈和電流，進而獲得轉子位置信息，但由于該方法一般采用查表法實現，因而需要占用大量的內存。為此文獻[7]提出了一種簡化磁鏈法，只需將事先存儲好的換相點磁鏈值與實時檢測的磁鏈值進行對比以實現換相控制，該方法雖然無需復雜的數學模型，但是其檢測精度不高，此外該方法不能獲得連續的轉子位置角度。文獻[8-11]提出了基于狀態觀察器法無位置估計方案，其最大的問題在于SR電機非線性模型難以準確建立，從而觀測器法只適用于SR 電機分段線性模型即不飽和運行情況。基于以上傳統方法缺陷，國內外學者提出了一些新型無位置傳感器檢測方法，迅猛發展的人工神經網絡技術也在SRM 轉子位置估計問題上得到了應用，如文獻[12-14]提出的基于神經網絡技術實現了轉子位置估計，這些方法不需要精確的SRM 系統數學模型，只要有足夠的訓練數據樣本即可擬合磁鏈、電流和轉子位置之間的映射關系，實現轉子位置估計，但神經網絡方法計算量較大，而且在訓練樣本數據時，需要花費大量訓練時間。文獻[15,16]假定SRM 繞組三相電感理想化為空間位置互錯120°電感矢量。通過空間矢量坐標變化方法，由三相電感空間矢量可以計算得到連續的轉子位置。該方法實現起來比較容易，簡單可靠，但是該文獻采用了非導通相注入脈沖法來檢測電感信息，難免會給電機帶來一定負轉矩、降低電機效率，同時也無法在較高轉速區域內運行。文獻[17]采用了激勵相磁鏈除以該相電流的方法獲得電機的電感信息，克服了文獻[15,16]中的缺陷，但是沒有分析電感級數模型隨電流增大發生飽和的情況。文獻[18]利用SRM 各相電感邏輯關系隨轉子位置區域性變化的特點，提出了一種電感分區比較式無位置技術。該方法簡單易于實現，但當電機工作在動態過程時，電感分區的交點會因電流發生變化而改變，從而導致位置估算誤差。

本文針對工作在不同飽和情況下的SRM 無位置傳感器四象限控制系統展開研究，以電機相電感傅里葉級數為基礎，研究了忽略三次以上諧波電感模型系數隨電流變化關系，提出了一種基于變系數電感模型的控制策略。利用電機變系數電感與轉子位置角度之間的關系，構建了四象限運行無位置傳感器控制系統。設計DSP 數字信號處理系統，采用軟件完成了轉子位置估計模塊，實現對開關磁阻電機的控制，最后通過實驗驗證了該方法的可行性。

2 電機電感級數展開模型的傅里葉變換分析

2.1 SRM 結構及特性分析

本文研究的SRM 類型為12/8 結構電機，電機結構如圖1 所示，定子與轉子均為雙凸極結構，定子極間距為30°，轉子極間距為45°，樣機單周期電感角度范圍為0°～45°，圖2 左為本文堵轉實驗獲得的18.5kW 開關磁阻電機電磁特性曲線，圖中灰色區域為電感線性區域，該區域磁鏈與電流成線性函數關系。而隨著電流的增大，由于SRM 嚴重的飽和效應，磁鏈的變化趨于飽和，與電流不再成線性變化關系。電磁特性曲線上下邊界和中間磁鏈分別對應著電機的最大、最小和中間電感位置，如圖2 右邊所示，其對應函數關系為

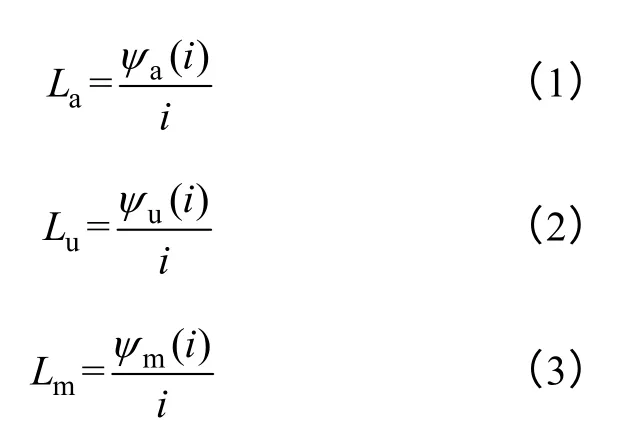
式中 ψa(i)，ψu(i) ——上下邊界磁鏈值；

ψm(i) ——中間磁鏈曲線數值。

最大電感La對應著轉子極與定子極完全對齊的位置；最小電感Lu對應著轉子極與定子極完全不對齊的位置；中間電感Lm對應著最大電感與最小電感的中間值。

圖1 12/8 SRM 電機結構Fig.1 The structure of 12/8 SRM

圖2 SRM 電磁特性曲線對應電感位置Fig.2 The electromagnetic characteristic curve of SRM corresponding inductance position

2.2 開關磁阻電機相電感模型

圖3 為樣機不同飽和情況下的相電感曲線，該曲線可以通過圖2 的電機電磁特性曲線間接計算獲得。對上述相電感進行傅里葉級數展開，可以獲得如下表達式

式中 Nr——轉子級數；

Ln——各項傅里葉級數前的系數；

ψn——各項級數的初相位。

圖3 不同電流下的實測電感波形Fig.3 The measured inductance with different currents

忽略高次項，得到簡化傅里葉級數電感模型[7]

式中，θelec為電角度，它和圖2 中的機械角度θm關系可以用以下的方程表示為

系數L0，L1和L2通過以下方程表示為

2.3 相電感模型系數擬合

由式（9）～式（11）可知，三相電感模型系數（L0、L1、L2）是由La、Lu和Lm決定，而La、Lu和Lm則是電流的函數。為此，根據圖2 的樣機電磁特性曲線數據可以得到L0、L1和L2隨電流（5～40A）的變化曲線，如圖4 中實線所示。可以看出，隨著電流增大，其三項系數數值呈逐漸減小趨勢，特別當電流達到了40A 時，L2的值近似為0，表明了此時樣機相電感二次諧波分量幾乎減小到0，只剩下基波分量和一次諧波分量。

為了能夠實時通過電流準確快速的獲得電感模型系數，本文采用擬合工具對L0、L1、L2隨電流變化曲線進行擬合，可以得到電感模型系數的解析表達式為

若次數n 取得太大會導致運算量過大，取的太小又難以達到理想的精度。由仿真可知，n=5 時即可達到較高的擬合精度，圖4 即為仿真所得擬合系數曲線與實際系數曲線的對比圖，圖中可以看出擬合精度完全能滿足要求，本文中五次擬合多項式表達式如下：

圖4 系數L0、L1、L2隨電流變化曲線Fig.4 The curve of L0、L1、L2with current changes

式（13）中各項系數擬合結果見表1。

表1 多項式各項系數值Tab.1 The coefficient values of polynomial

在電機運行時，只需將采樣得到的電流值代入以上系數公式即可計算出對應該電流情況下的電感模型系數值。

3 基于電感模型的轉子位置檢測原理

3.1 電機電感估算策略

本文采用電感模型實現轉子位置估算，必須實時的獲取電機激勵相電感值。SRM 相電壓方程可以表示為以下形式：

式中 udc——母線電壓；

Rk——電機相電阻；

ik——相電流；

ψk——激勵相磁鏈。

將等式（14）變形，可以得到激勵相磁鏈的積分形式，如下：

式中 T——磁鏈積分時間。

本文采用的是傳統的不對稱半橋功率變換器，在電流斬波控制方式下，繞組兩端電壓有udc、0、-udc三種狀態，故上式中sk表示為

激勵相磁鏈ψk和該相電感之間的關系表示為

結合以上式（15）和式（17），激勵相電感可以通過以下公式計算出來

當電機A、B、C 三相中某相被激勵時，即可由母線電壓udc和電流傳感器測得的相電流ik計算出該相電感值。

3.2 電感計算角度原理

獲得激勵相電感之后，利用傅里葉級數展開的電感模型與轉子位置角度之間的函數關系，即可估算出轉子位置角度，以B 相電感為例，將方程（6）變形為電感LB與電角度θelec余弦形式，即

求解出電角度θelec的余弦表達式，如下

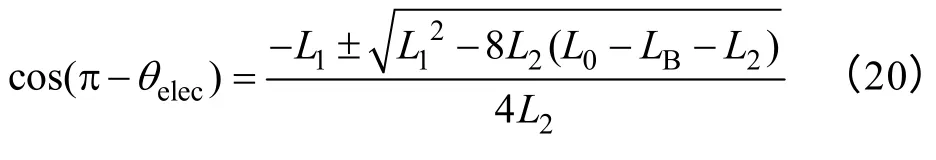
由于cosθ 數值范圍為-1 到1，所以式（20）分子應取正號，即上述等式簡化為

由此可以得出轉子位置電角度θelec的表達式為

根據式（5）～式（7）三相電感表達式，不難得到A 相和C 相估算轉子位置公式。但本文為了軟件程序簡化，對于A、C 仍然采用式（22）估算角度，當A、B、C 三相中某相激勵時，將該相電流通過式（18）計算出的相電感值代入到式（22）即可計算出轉子位置估計值。最終，估算角度同實際角度之間的關系見表2。

表2 估算角度同實際角度之間的關系Tab.2 The relationship between estimatd position and real position

3.3 無傳感器換相控制

通過三相輪流導通激勵，開關磁阻電機才能夠被驅動旋轉。在圖5 中，三相電感LA，LB和LC互錯120°電角度。為了角度能夠連續估計，開通角θon和關斷角θoff必須滿足下列條件

同時導通角必須滿足

圖5 中標出了θon，θoff和θcond的對應關系。圖5a 給出了電動模式下利用相電感估算角度的過程。由圖可知，進行連續角度估計每相只需提供15°范圍內的電感值。圖5a 中，由于相電感在4°～19°三相電感實線部分范圍內的上升區域變化比較明顯，因此本文將實線部分電感組合成三相合成電感進行角度估算。圖5b 給出了電動模式下利用三相合成電感估算角度的過程。制動狀態下，角度估算過程同電動模式基本類似，但由于θon，θoff的變化，與4°～19°對稱的下降區域三相電感實線部分組合成三相合成電感進行角度估算。從圖5 可以看出，在電機工作在電動狀態下，估算的角度是上升的；工作于制動狀態時，電機繞組是在電感下降區勵磁，故估算出的角度成下降趨勢。在一個完整換相周期內，通過A、B、C 三相繞組分別被激勵時所估算出的角度θa、θb、θc實現對電機的換相控制。

圖5 不同工作狀態下三相合成電感角度估算Fig.5 The angle estimation of three-phase inductor under different working conditions

4 靜止起動初始位置估計方法

要實現電機無反轉起動，就必須準確的獲取電機轉子的初始位置，為此本文采用脈沖注入的方式來獲取電機靜止起動時初始導通相。靜止狀態下的激勵脈沖法原理如圖6 所示，在電機靜止起動瞬間，對SRM 通以短時的電壓脈沖激勵。

圖6 激勵脈沖法原理Fig.6 Principle of excitation pulse method

將式（17）代入式（14）并取任意一相可得

式中 L (i,)θ ——相電感；

對電機三相繞組同時注入直流電壓為514V 的為高頻激勵脈沖，得到不同的三相響應電流，比較三個響應電流的大小決定初始導通相。然而脈沖頻率過高會導致三相激勵電流幅值過小，脈沖頻率過低也容易使激勵電流進入飽和區域，從而影響初始相的準確判斷，為此我們選擇頻率為4kHz 的高頻激勵脈沖。具體電機無反轉運行起動工作相選擇見表3。

從表3 中可以看出，為了保證較大的起動轉矩，對于三相12/8 電機，運行時雖然為單相輪流導通，但在起動時有兩相繞組同時工作的情況。

表3 起動初始工作相選擇Tab.3 The initial phase selection when start

5 無位置控制系統實現

5.1 起動狀態兩種位置估計方法過渡

圖7 為起動到正常運行過程中兩種位置估計策略的切換過程，靜止起動時，向三相繞組注入短暫脈沖獲得初始轉子位置信息。當初始導通相確定并開始勵磁后，繞組中電流迅速建立起來，此時立刻切換為電感模型估算轉子位置角度，由估算出的轉子位置角度對電機進行準確換相，從而實現無反轉起動并穩定運行下去。

圖7 系統位置估算切換策略Fig.7 The switching case of position estimation strategy when start

5.2 系統閉環控制實現

圖8 中虛框內軟件部分由DSP 和可編程邏輯器件（EP1K30）構成的混合控制器實現，包含以下幾個部分：

（1）轉速差?ω 經過PI 調節器獲得給定斬波限電流Iref，并結合CCC 脈沖發生器完成轉速閉環控制。

（2）通過A-D 采樣模塊電壓傳感器測得的母線電感值udc和電流傳感器測得的勵磁相電流值Ia、Ib、Ic轉變為數字處理器DSP 所能識別的數字信號。

（3）繞組相電壓可以利利用開關信號（PWMST）和母線電壓值udc根據式（16）重構，磁鏈計算模塊再根據式（15）在扣除繞組電阻壓降的基礎上積分獲得磁鏈。

（4）磁鏈ψ、相電流iabc和估算角度相選擇信號（Active）輸入到相電感計算模塊根據式（18）算出該相電感?L。

（5）根據式（13）得到簡化電感模型的三項系數L0、L1、L2，與相電感值?L 一同送入角度推算模塊，根據式（22）算出轉子位置角度?θ。

（6）換相控制器根據估算角度?θ 實現對電機的換相控制，并根據換相時間間隔計算轉速?ω。

圖8 無位置控制系統實現原理圖Fig.8 Sensorless control system implementation principle

5.3 四象限運行控制

SRM 四象限運行通過如下方法實現，首先根據式（18）對導通相電感進行連續計算。由圖9 可見，用來估算角度的相電感處在上升區域還是下降區域，由具體的工作的象限決定。圖中第Ⅰ、Ⅱ、Ⅲ、Ⅳ象限分別為正向電動、正向制動、反向電動和反向制動四種運行狀態。其次，系統根據估算角度和具體所在的工作象限決定換相點，實現換相控制，具體換相細節見3.2 節。

圖9 四象限實現原理圖Fig.9 Principle of SRM four-quadrant sensorless implementation

在電機運行在額定轉速1 000r/min 以下時，系統采用開通關斷角固定的電流斬波控制（CCC）方式，在電動狀態時開通角和關斷角分別為0°和19°，制動開通角和關斷角分別為22.5°和40°，而電機運行在額定轉速以上時采用角度區間控制（APC）方式。

6 實驗結果驗證

6.1 實驗硬件條件和參數

為驗證本文所提無位置控制策略的可行性，以DSP+FPGA 為控制系統核心，構建了實驗平臺（見圖10），采用一臺18.5kW SRM 為實驗樣機，進行了實驗驗證。以德州儀器（TI）公司的TMS320F2812 DSP 為核心控制芯片，負責靜止起動轉子初始位置判斷、簡化電感模型實時估算轉子位置以及對電機進行斬波控制。12 位的ADC 采樣芯片ADS7864 負責實時采樣，IGBT 開通關斷信號經過ALTERA 公司的EP1K30QC208 FPGA 邏輯綜合處理后再送給驅動模塊。功率變換器采用三相不對稱半橋電路，主開關器件IGBT 采用英飛凌公司的FF150R12KE3G。系統實物圖如圖11 所示，樣機額定參數見表4。

圖10 SRM 實驗平臺結構Fig.10 Structure of SRM experimental bench

圖11 無位置控制系統實物圖Fig.11 Hardware of the sensorless control system

表4 樣機參數Tab.4 The parameters of prototype

本文采用的無位置傳感器算法中所進行的電感辨識、電感模型三項系數計算、基于電感模型的無位置估計和轉速估計，均利用DSP 控制器中的軟件實現。TMS320F2812 將高性能的DSP 內核和豐富的微控制器外設功能集于單片之中，其運算能力達到每秒執行150 兆條指令（150MIPS），這使其能夠提供比傳統16 位微處理器強大得多的性能，電壓、電流通過高速采樣芯片ADS7864 采樣。算法各子函數運算所需的時間如圖12 所示，磁鏈積分計算和速度估算所需時間分別為6.03μs 和5.098 7μs，而采用本文提出的算法實現轉子角度估算模塊僅需 3.229 4μs，可以看出，算法實現過程所需計算量較小。

圖12 無位置傳感器程序各模塊運行時間Fig.12 Time schedule for each module of sensorless program

6.2 靜止起動初始位置估計

圖13a 給出了電機由靜止起動時的定子繞組三相電流波形，從波形中可以看出起動前對三相繞組注入了短暫的脈沖信號，通過定子繞組中的響應電流大小來判斷轉子的初始導通相，圖中響應電流滿足Ia＞Ib≥Ic，故起動相為A、C 兩相。圖13b 給出了起動時角度估計波形，可以看出起動時角度估算均勻平滑，電機無抖動，驗證了本文采用的脈沖注入法能夠精準地獲得初始位置并實現無反轉起動。

圖13 初始位置檢測及起動時角度估計Fig.13 Position estimation at standstill and angle estimation when start

6.3 三相合成電感估算過程

圖14 給出了三相合成電感和位置估算的波形，轉速在300r/min 左右。從上往下依次為電流、磁鏈、合成電感和估算出的角度。從圖中可以看出，由于相電感處于線性非飽和區域，因此三相電感合成成鋸齒波。合成電感最大值0.08H，最小值0.01H。角度估算結果如前所述在4°～19°之間。

圖14 三相合成電感估算過程（300r/min）Fig.14 Inductance identification process at 300r/min

6.4 穩態運行時無位置角度估計

為驗證不同轉速穩態運行條件下該算法無位置傳感器角度估計的可靠性，分別給出了100r/min、500r/min、1 000r/min、1 350r/min 四種不同轉速運行條件下的角度估計波形。圖15a 中可以看出，由于估算出的位置范圍為4°～19°，而由位置編碼器計算的實際位置是由0 開始，故造成單個電周期內估算位置與實際位置首尾錯開 4°（見圖中的區域1），由圖中虛線標出的區間可以看出，估算角度波形中1、2、3、4 四個區域正好構成一個電周期，對應著0°～45°一個周期內實際角度。由圖15 可以看出，從較低轉速（100r/min）到電機的最高轉速（1 350r/min），該算法估算出的轉子位置都具有較好的精度。

圖15 不同轉速下實驗波形Fig.15 Experimental waveforms at different speeds

6.5 閉環系統加減速動態性能分析

為驗證轉速突變情況下無位置閉環控制系統的動態性能，圖16a、16b、16c 依次給出了加載條件下0r/min→400r/min→800r/min→350r/min 整體動態運行波形和加減速過程瞬間波形。圖16b 與圖16c分別為加速和減速瞬間波形，圖16c 中可以觀察到在給定轉速突減的瞬間，電機工作狀態立即由電動變為制動，圖中圈出的瞬間角度估計波形及電流波形可以看出此時A、B、C 三相繞組已經變為電感下降區域勵磁，估計角度波形由上升變為下降。圖16a 為無位置轉速閉環系統整體加減速動態波形，動態波形中可以看出，在給定轉速突變的情況下，實際轉速只需不到0.5s 的時間即可迅速達到給定轉速，表明了所提出的無位置閉環控制系統具有較高的響應速度和較好的跟隨性能。

圖16 加減速動態實驗波形Fig.16 Dynamic experimental waveforms of acceleration and deceleration

6.6 閉環系統正切反動態性能分析

為進一步驗證本文提出的無位置轉速閉環控制系統的動態性能，圖17a 給出了加載條件下給定轉速由正1 000r/min 瞬間切為負1 000r/min 時閉環系統的動態運行波形，由圖可見，整個換向過程中，電機先進入制動工作狀態，實際轉速由穩態1 000r/min 迅速減小，經過短暫的0r/min 過渡階段之后再反向加速到穩態，換向過程約1.2s 左右。圖17b 為正切反瞬間波形，圖中可以清晰的看到換向瞬間的轉子位置估計情況，由估計的角度可以看出換向過程經過200ms 左右零速的過渡區域，結合圖17a 可知電機換向過程平穩可靠，沒有出現較大的抖動，進一步驗證本文提出的角度估計策略具有較高的動態性能。

圖17 正切反動態實驗波形Fig.17 Dynamic experimental waveforms of speed reversal

6.7 實測機械特性分析

利用液壓閘使電機堵轉，并逐漸降低負載轉矩直到電機臨界轉動點，記錄零速負載轉矩值，完成起動轉矩的測量；電機驅動運行時，將電機穩定在某一恒定轉速值，通過液壓閘逐漸增大負載，并同時觀察電流波形與轉速，當三相繞組電流到達最大電流限時，繼續增加負載，電機的轉速就會下降，若下降的轉速超出允許動態速降則記錄此時的負載轉矩值。采用該方法對實驗樣機在不同轉速下進行多次測量，可以獲得圖18 所示的18.5kWSRM 樣機0～1 400r/min 轉速范圍內的實測機械特性曲線。圖中可以看出在額定轉速以下 SRM 呈恒轉矩特性，而在額定轉速以上SRM 呈恒功率特性。

圖18 SRM 樣機實測機械特性曲線Fig.18 Mechanical characteristics cure of SRM

7 總結

本文提出了一種新型的無位置傳感器控制策略。該方法通過磁鏈積分除以電流的方式間接獲得三相合成電感，并根據變系數電感模型完成位置估計。在靜止狀態該方法結合脈沖注入方法，并能夠完成從靜止到高速運行的平滑過渡。更進一步，設計并實現了四象限不同工況下工作相選擇和切換控制。利用PI 調節器構成速度閉環后，利用該方法構成的無傳感器系統通過了一系列加減速瞬態測試。實驗結果表明，本文提出的四象限無傳感器技術完全可行，并可以推廣應用。該技術尤其適合于需要四象限運行的場合。且外，該方法不需要附加任何硬件，雖然控制算法涉及到開方和反余弦計算，使得整體運算量有所增加，但對于現有的數字信號處理器和微控制器是可以接受的。因此比較容易實現，也容易修改并適用于其它類型的開關磁阻電機。上述這些特點使得該方法非常實用，可靠且成本低，可以被許多低成本變速應用場合接受。實驗結果充分驗證了本文提出的無位置傳感器方案，并證明了它的優點。

[1]Krishnan R.Switched reluctance motor drives:modeling,simulation,analysis,design and applications[M].Boca Raton,FL:CRC Press,2001.

[2]Ehsani M,Fahimi B.Elimination of position sensors in switched reluctance motor drives:state of the art and future trends[J].IEEE Transactions on Industrial Electronics,2002,49(1):40-47.

[3]吳紅星,倪天,郭慶波,等.開關磁阻電機轉子位置檢測技術綜述（一）[J].微電機,2011,44(3):76-83.Wu Hongxing,Ni Tian,Guo Qingbo,et al.Summary of detecting rotor position technique for switched reluctance motors[J].Micro Motors,2011,44(3):76-83.

[4]Gallegos L G,Kjaer P C,Miller T J E.High-grade position estimation for SRM drives using flux linkage/current correction model[J].IEEE Transactions on Industry Applications,1998,34(4):859-869.

[5]Koblara T,Sorandaru C,Musuroi S,et al.A low voltage sensorless switched reluctance motor drive using flux linkage method[C].International Conference on Optimization of Electrical and Electronic Equipment,2010:665-672.

[6]Lyons J P,MacMinn S R,Preston M A.Flux-current methods for SRM rotor position estimation[C].Conference Record of the IEEE Annual Meeting on Industry Applications Society,1991:482-487.

[7]邱亦慧,詹瓊華,馬志源,等 .基于簡化磁鏈法的開關磁阻電機間接位置檢測[J].中國電機工程學報,2001,21(10):59-62.Qiu Yihui,Zhan Qionghua,Ma Zhiyuan,et al.The indirect position sensing of SRM on the basis of simplified flux method[J].Proceedings of the CSEE,2001,21(10):59-62.

[8]Tan Guojun,Ma Zhenglan,Kuai Songyan,et al.Four-quadrant position sensorless control in switched reluctance motor drives based on sliding mode obverser[C].International Conference on Electrical Machines and System,2009:1-5.

[9]Islam M S,Husain I,Veillette R J,et al.Design and performance analysis of sliding-mode observers for sensorless operation of switched reluctance motors[J].IEEE Transactions on Control Systems Technology,2003,11(3):383-389.

[10]Elmas C,Parra H Z L.Application of a full-order extended Luenberger observer for a position sensorless operation of a switched reluctance motor drive[C].IEE Proceedings of Control Theory and Applications,1996:401-408.

[11]Jain A K,Mohan N.Dynamic modeling,experimental characterization,and verification for SRM operation with simultaneous two-phase excitation[J].IEEE Transactions on Industrial Electronics,2006,53(4):1238-1249.

[12]Desai P C,Krishnamurthy M,Schofield N,et al.Novel switched reluctance machine configuration with higher number of rotor poles than stator poles:concept to implementation[J].IEEE Transactions on Industrial Electronics,2010,57(2):649-659.

[13]蔡燕,許鎮琳,高超.基于神經網絡非線性模型的開關磁阻電機調速系統動態仿真[J].電工技術學報,2006,21(8):25-30.Cai Yan,Xu Zhenlin,Gao Chao.Simulation of SRD based on neural net nonlinear model[J].Transactions of China Electrotechnical Society,2006,21(8):25-30.

[14]紀良文,蔣靜坪,何峰.基于徑向基函數神經網絡的開關磁阻電機建模[J].電工技術學報,2001,16(4):7-11.Ji Liangwen,Jiang Jingping,He Feng.Modeling of switched reluctance motors based on radial basis function neural network[J].Transactions of China Electrotechnical Society,2001,16(4):7-11.

[15]Misawa S,Miura Y,Miki I.A rotor position estimation for 3-phase switched reluctance motor based on complex plane expression[C].International Conference on Electrical Machines and Systems(ICEMS),Japan,10-13 Oct,2010.

[16]Cai Jun,Deng Zhiquan.Sensorless control of switched reluctance motor based on phase inductance vectors[J].IEEE Transactions on Power Electronics,2012,27(7):3410-3423.

[17]Misawa S,Kawasaki.A rotor position estimation using Fourier series of phase inductance for switched reluctance motor[C].2010 International Symposium on Power Electronics Electrical Drives Automation and Motion(SPEEDAM),Japan,14-16 June,2010.

[18]周竟成,王曉琳,鄧智泉,等.開關磁阻電機的電感分區式無位置傳感器技術[J].電工技術學報,2012,27(7):34-40.Zhou Jingcheng,Wang Xiaolin,Deng Zhiquan,et al.The position sensorless technology of switched reluctance motor based on the regional comparison of three-phase inductance[J].Transations of China Electrotechnical Society,2012,27(7):34-40.