基于滯后補償的PWM 逆變器控制策略研究

劉寶其 段善旭 陳昌松 方支劍

（強電磁工程與新技術國家重點實驗室（華中科技大學）武漢 430074）

1 引言

大功率儲能系統的建設離不開功率調節系統（Power Conditioning System,PCS）的研究。儲能系統中的PCS 一般采用雙向高頻PWM 變換器加雙向直流變換器構成雙級式能量變換系統，或直接采用雙向高頻PWM 變換器加相應的直流濾波電感構成能量變換系統，根據用戶需求變換器可以工作于并網狀態或者離網狀態[1-3]。當PCS 離網運行時，其工作特性與逆變器一致，針對其輸出波形控制技術，國內外學者提出許多優良的數字控制方法，主要包括單閉環PID 控制、雙閉環控制、無差拍控制、重復控制、狀態反饋控制、滑模變結構控制、微分平滑控制和基于模糊控制和神經網絡控制的智能控制等算法[4-10]。其中單閉環控制算法簡單、魯棒性強，但對非線性負載適應較弱；重復控制能夠消除周期性的擾動影響而獲得較好的輸出電壓波形，但是動態響應速度較慢[11]；狀態反饋法一般只針對空載建立，需對負載擾動采取針對性的措施[12]；而智能控制算法則通常需要進行復雜的運算，運用相對較少。

基于極點配置的雙閉環設計具有很好的控制性能，傳統的極點配置為求簡便，一般基于連續域進行設計，被控對象為二階模型，根據“控制參數量與控制自由度相等的原則”，此時可以任意配置系統的極點以獲得期望的動態響應特性[13,14]。但是采用數字控制時，由于采樣、計算延時限制了系統輸出占空比，甚至會引起系統的不穩定。為了防止占空比受限，通常采用滯后一拍控制，從而使逆變器控制對象由原來的二階系統升高為三階，此時控制系統不再滿足極點配置的條件了。文獻[15,16]分別通過在對象建模時考慮延時和提前時刻采樣，解決了占空比受限的問題。文獻[17]采用觀測器預測系統的狀態變量，消除滯后一拍的影響，然而由于系統模型誤差和建模誤差的影響存在較大的預測誤差。文獻[18]在觀測器中加入重復控制補償預測誤差，取得較好的穩態和動態性能，卻增加了控制系統的復雜度，降低了系統穩定性，尤其是針對三相系統需用到的狀態觀測器數目較多，在開關頻率較高的系統這是難以接受的。

為此，本文通過分析了離散域下逆變器控制參數量與系統階數的關系，引入控制器輸出量作為系統狀態變量，并引入相應的反饋系數，使得離散化后系統的控制自由度增加一個，從而滿足任意配置極點的條件。分析表明，系統引入新狀態變量且采用雙環控制策略時，內、外環控制器可以選擇P控制器、PI 控制器、PD 控制器或者PID 控制器的任意組合，通過配置不同的反饋系數均可獲得良好的動態性能，并且該方法具有簡單可靠、方便實現的特點。最后，本文設計了基于增廣狀態變量的電感電流內環、電容電流外環的雙環控制策略，仿真和實驗表明該方法具有良好的動靜態特性。

2 PWM 逆變器模型

圖1為三相逆變器的主電路圖，交流側為LC濾波器，rL為考慮逆變器濾波電感L 內阻、死區效應、開關管導通壓降和線路阻抗等各種阻尼因素的綜合等效電阻，Zload表示系統負載（輸出通過一個180:380 的D11Yn 型變壓器連接負載，圖1 中未畫出），逆變器的關鍵參數見表1。

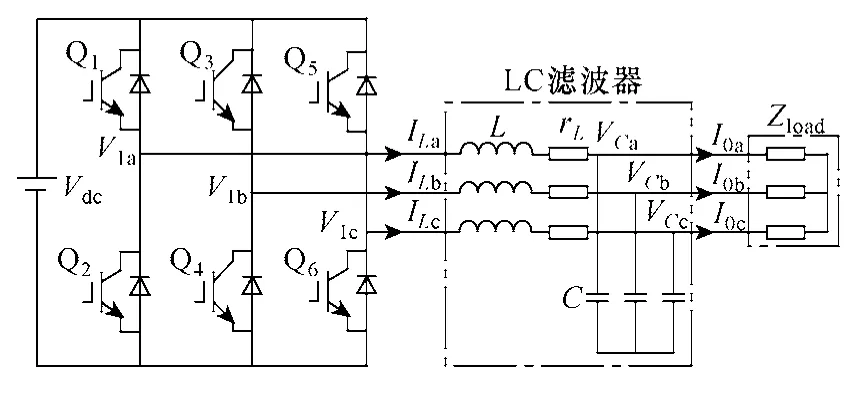
圖1 三相逆變器主電路結構圖Fig.1 Main circuit of a three-phase inverter

由圖1 可知，假設開關管均為理想器件，建立三相靜止坐標系下的系統模型，并轉換到同步旋轉坐標系下（假設已完成dq 軸之間的解耦），則可建立d 軸分量在連續域下的狀態空間表達式如式（1）所示，其連續域模型則如圖2 所示（q 軸分析與d軸類似）。

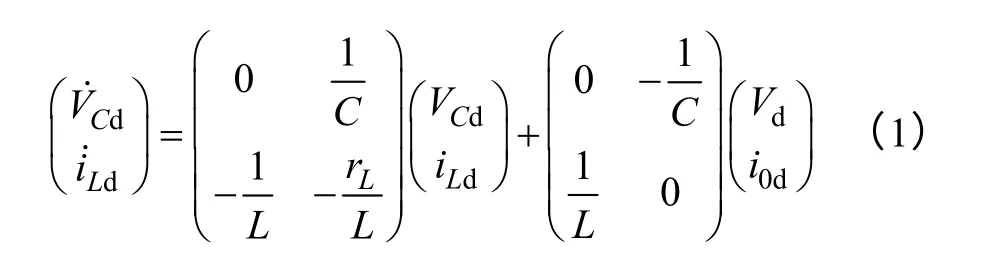
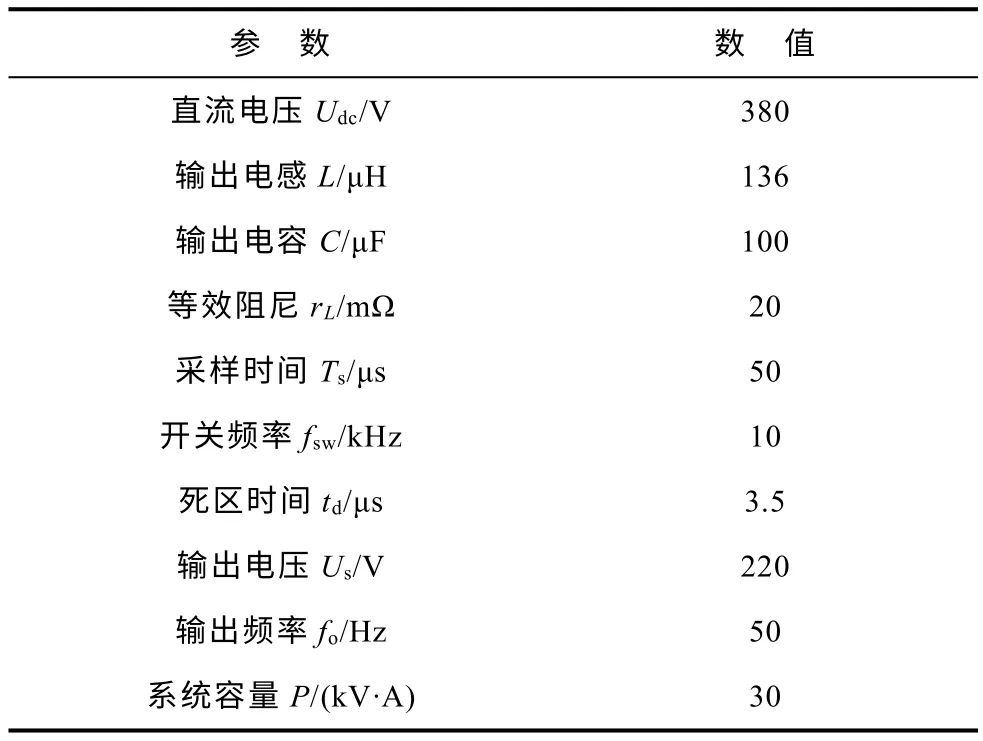
表1 逆變器電路的關鍵參數Tab.1 Key Parameters of the inverter

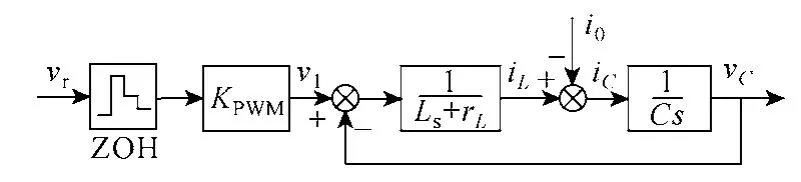
圖2 逆變器系統連續域模型Fig.2 Inverter model in continuous domain

圖2 中，vr為數字控制器的輸出量，經過零階保持器實現數模轉換后作用于逆變器系統。由于采用直接數字化設計可以在保證系統穩定性的同時獲得更寬的控制帶寬，因此被廣泛運用。假設系統采樣時間均為Ts，則由式（1）可推出離散域下，電感電流iL到逆變器端口電壓v1的傳遞函數為

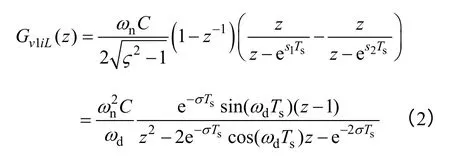
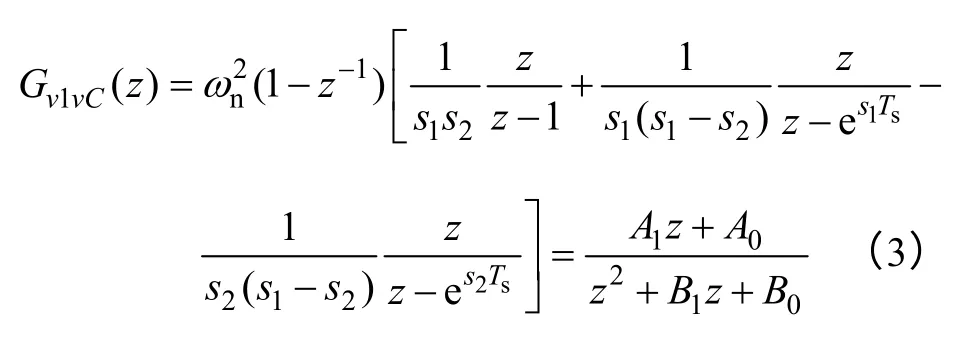
電感電流iL到電容電壓vC的傳遞函數為

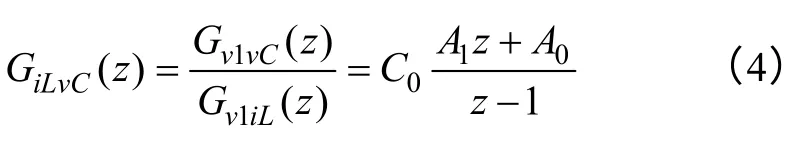
式中

則由式（3）～式（5）可得出逆變器系統離散域模型如圖3 所示，KPWM為逆變器的橋臂增益，并對各反饋系數進行歸一化處理。

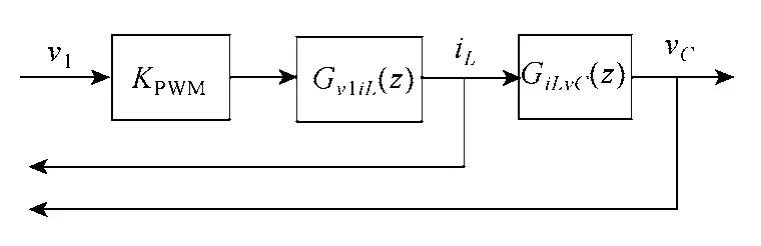
圖3 逆變器系統離散域模型Fig.3 Inverter model in discrete domain

3 基于滯后補償的控制策略

3.1 控制參數量與控制自由度關系

從前節的建模分析可知，基于LC 濾波器的逆變器，不論單環結構還是雙環結構（電感電流內環或者電容電流內環），在未加控制器且采用滯后一拍控制時，其閉環傳遞函數可表示為

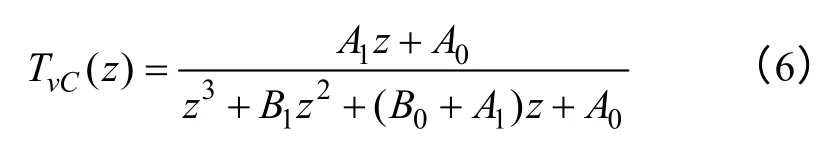
可見，滯后一拍環節的引入使得逆變器離散域模型增加為3 階，代表系統的3個被控自由度。在此基礎上，如果引入控制環節，則采用不同的離散化方法可以得到控制參數（可控自由度）與系統階數（被控自由度）的關系見表2（采用雙環控制策略，且雙環均為同類型的控制器）。

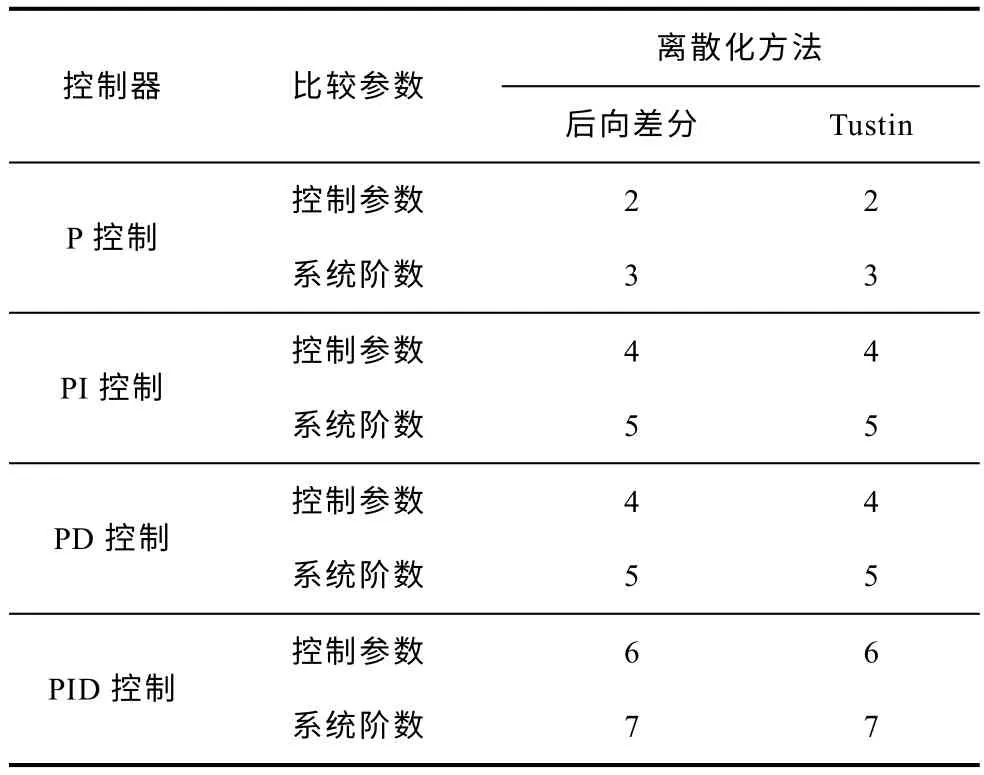
表2 考慮滯后一拍時，控制參數與系統階數的關系Tab.2 The relationship between DOF of controller and DOF of system when one-step-delay is considered

由表2 可知，離散化逆變器系統引入滯后一拍控制環節后，系統的可控自由度和被控自由度始終相差為1。同理，當內、外雙環采用不同類型控制器，或者采用其他離散化方法時也可以得到相同的結論。

3.2 增廣狀態變量的選取和分析

文獻[13]指出系統的控制參數量（可控自由度）與系統階數（被控自由度）相等是高性能逆變器控制實現的基礎，也是實現系統極點任意配置的條件，因此，需要為系統增加一個可控自由度。針對逆變器系統，可選取電感電流、電容電流、電容電壓三者的積分或者微分環節為新的狀態變量。但是，在引入前述幾種狀態變量的同時也增高了系統的階數，仍然不滿足“控制器可控自由度與系統被控自由度相等”的約束條件。為此，本文引入控制器的輸出量vr為增廣狀態變量，并引入Kz為其反饋系數，以構建新的逆變器離散域模型，其控制框圖如圖4 所示。

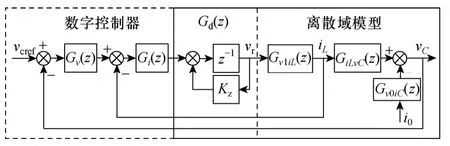
圖4 基于增廣狀態變量的控制框圖Fig.4 Control block based on augmented state-variable

圖4 中，對KPWM和各采樣通道的反饋系數進行了歸一化處理，故均略去；z-1表示系統采用滯后一拍控制；Gv(z)和Gi(z)分別為電容電壓外環和電感電流內環的控制器；Gi0vC(z)為系統的閉環輸出阻抗；Gd(z)則表示由增廣狀態變量構成的新環節，對于離散系統，它既由控制器實現，同時也屬于離散域模型的一部分。

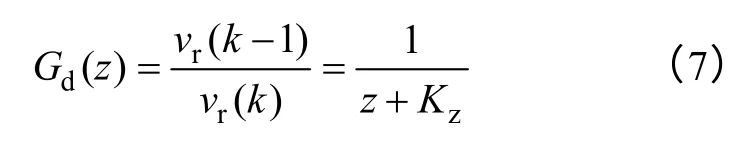
其等效于對滯后一拍環節進行了修正，畫出Kz變化時Gd(z)的Bode 圖如圖5 所示，且由式（7）可得Gd(z)的相頻特性為

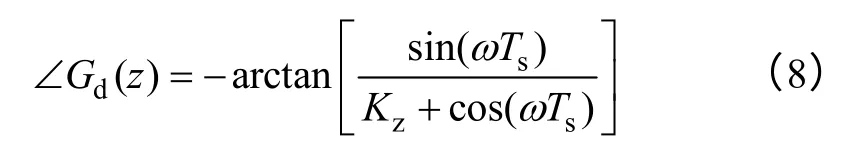
由圖5 和式（8）可知

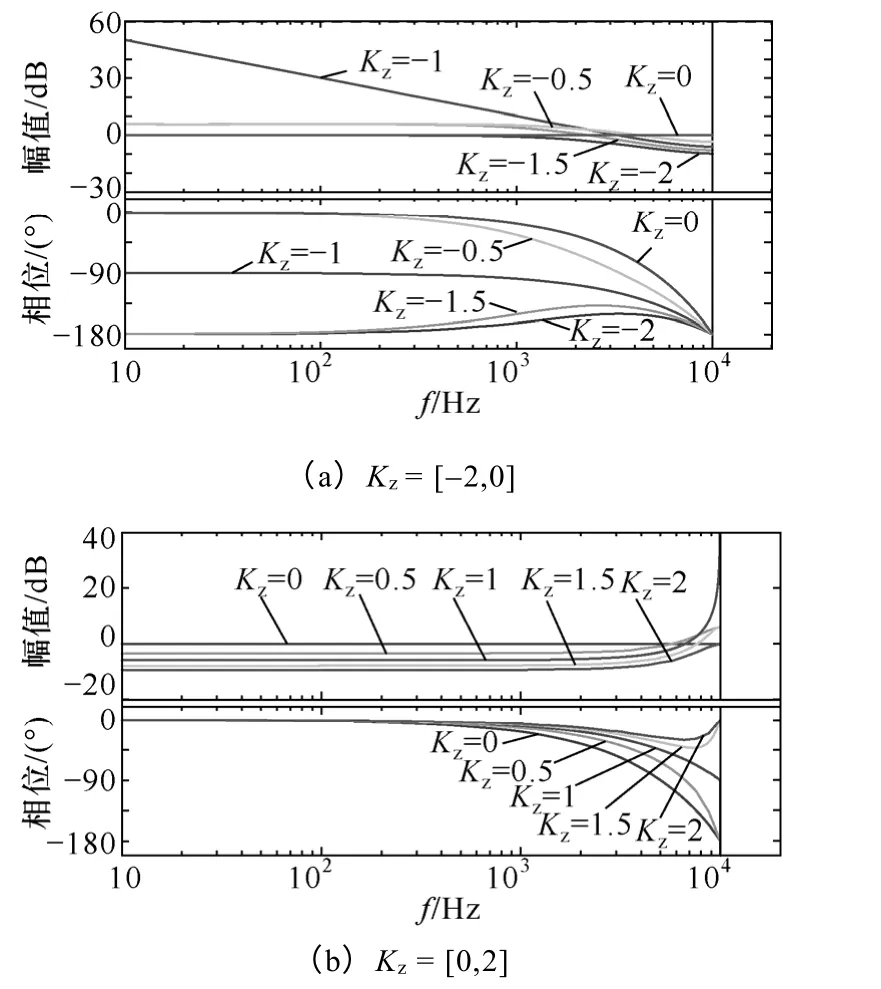
圖5 延時環節的Bode 圖Fig.5 Bode diagram of delay link

（1）當Kz=[-2,0)時，延時環節引入的極點位于z 域的右半平面，且隨著極點的右移，Gd(z)產生的相位滯后越大，尤其是當極點右移至單位圓外后，其引入的低頻段相位滯后超過90°，這對原本存在相位滯后的二階逆變器系統是極為不利的，特別是采用傳統的PI 控制時，控制器本身還會引入相位滯后，因此Kz＜0 的情況不予考慮。

（2）當Kz=0 時，延時環節退化成滯后一拍環節，其引入的相位滯后為(360fTs)°，在1kHz 處引入的相位滯后達18°，極大地降低了系統的穩定裕度，尤其是對開關頻率較低的大功率逆變器系統，其引入的相位滯后更為嚴重。

（3）當Kz=（0,2]時，延時環節引入的極點位于z 域的左半平面，且隨著極點的左移，Gd(z)產生的相位滯后越小。需要注意的是，當極點左移至單位圓外后，其引入的低頻段相位滯后進一步減小，并在高頻段轉為上升使得乃奎斯特頻率處的相位滯后減為0，即∠Gd(z)|ω=π/Ts=0。

同樣，Gd(z)的幅頻特性可表示為

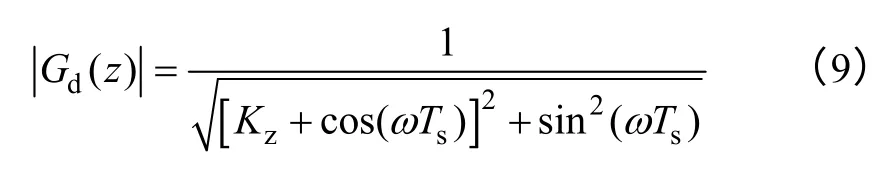
在ω=(0,1/(2Ts))范圍內，|Gd(z)|單調遞增，且隨著Kz的增大，|Gd(z)|減小。當Kz=2 時，直流分量的幅值增益比滯后一拍控制時降低9.54dB，但是可以很方便地通過控制器對其增益進行補償。因此，可以通過選取Kz為合適的正數用于補償滯后一拍控制產生的相位滯后，并通過式（8）和式（9）分別計算出其對應的相位和幅值，然后進行控制器的時域設計。此種設計方法，可以精確地計算出控制器需要補償的相位和幅值，有利于提升系統的控制帶寬，提高系統動態性能。

3.3 基于極點配置的雙閉環控制策略

為了優化系統的動態特性，本文采用極點配置法對圖4 所示的控制系統進行參數設計。分別求出電感電流內環的開環和閉環傳遞函數、電容電壓外環的開環和閉環傳遞函數、系統閉環輸出阻抗的傳遞函數，如下所示。

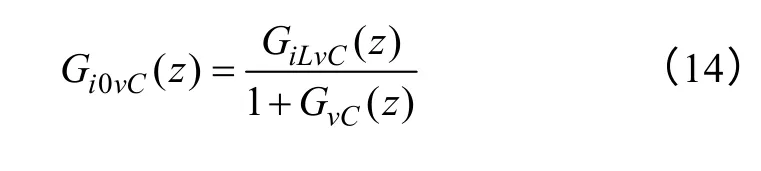
由圖4 可知，輸出電壓同時受ΦvC(z)和Gi0vC(z)的影響，為了保證系統的穩態精度和魯棒性，本文設計的控制器內、外環均采用PI 補償器，即

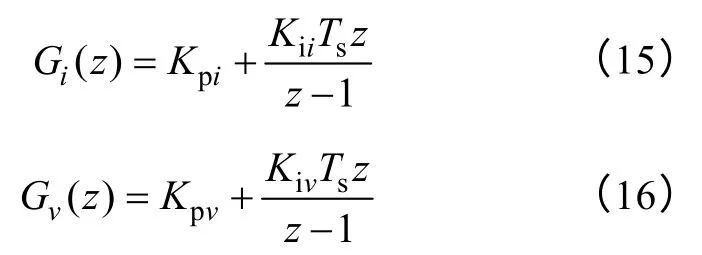
則由式（13）可求出逆變器系統的特征方程為

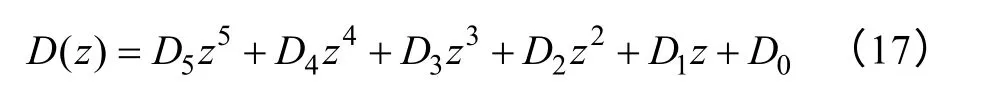
式中，Di(i=0,1,···,5)為系統特征方程的系數，其與系統參數、采樣時間以及Kpi、Kpv、Kii、Kiv、Kz這5個控制參數相關。因此，引入新的狀態變量后，系統階數和控制參數量是相同的，系統的極點可實現任意配置。取系統期望的主導極點對應的阻尼比為ζλ=0.7，對應的自然諧振頻率為ωλ=4 000rad/s，同時令系統的3個非主導極點相等，且都位于實軸上，其距虛軸的距離10 倍于主導極點，則此時系統的5個極點分別為

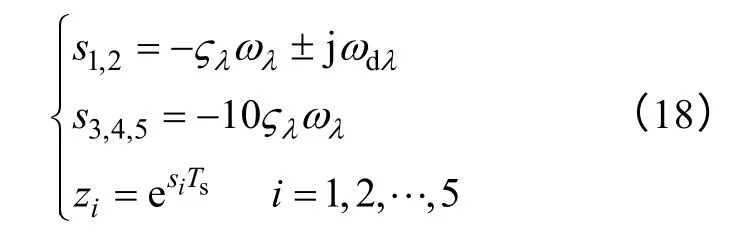
畫出系統相應的Bode 圖如圖6 所示，系統的相位裕度為43°，閉環帶寬為1.74kHz 左右，具有較好的穩定裕度和較快的響應速度。圖7為系統的根軌跡圖和閉環零極點分布圖，通過極點配置法將原本處于不穩定和臨界穩定的系統極點配置在期望的極點位置上。系統的輸出阻抗Bode 圖如圖8 所示，其在工頻處的輸出阻抗為阻感性，數值為0.318Ω，可通過負載電流前饋環節消除其對系統輸出電壓的影響[17]。

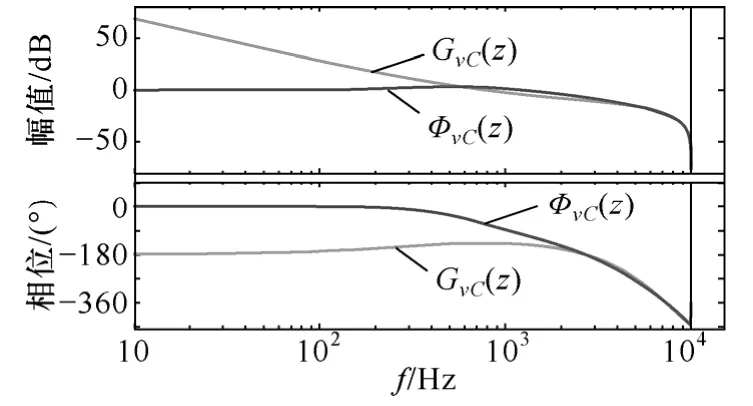
圖6 逆變器系統Bode 圖Fig.6 Bode diagram of the inverter system

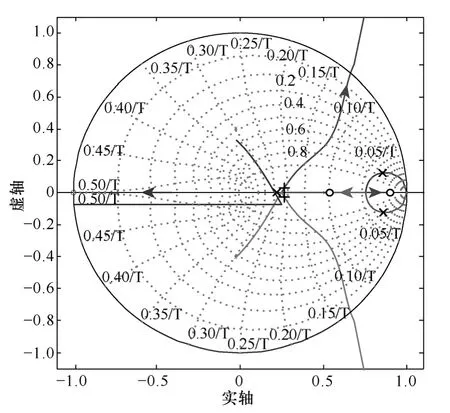
圖7 逆變器系統根軌跡圖Fig.7 Root locus of the inverter system

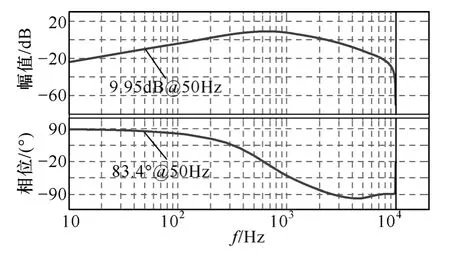
圖8 逆變器系統輸出阻抗Bode 圖Fig.8 Bode diagram of the output impedance of the system

4 仿真與實驗分析

4.1 仿真分析

根據表1 所示的參數，運用Matlab 對逆變器進行建模仿真，波形如圖9 所示。圖9a為系統突加、突減阻性負載時的輸出電壓波形，滿載時THD=1.18%，空載時THD=1.23%，且空載和滿載的穩態誤差均小于0.2%。圖9b為負載突變時A相輸出電壓和輸出電流的仿真波形，其中卸載過程中輸出電壓超調為8.8%，調節時間小于2ms；突加負載過程中，輸出電壓的超調約為7.9%，調節時間小于3ms，系統具有較快的動態響應速度。圖9c為逆變器帶非線性負載（采用電容濾波的三相不控整流接電阻負載）的輸出電壓和電流波形。此時，由于前饋環節并不能完全消除輸出阻抗的影響，輸出電壓上產生了與輸出電流頻次相同的低次諧波，其THD=3.09%，滿足5%的設計要求。

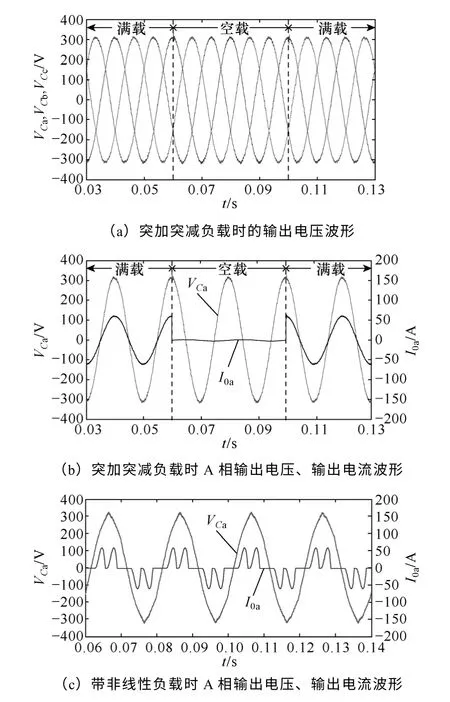
圖9 逆變器仿真波形Fig.9 Waveforms of inverter by simulation

4.2 實驗結果分析

為了驗證本文所提的控制策略，研制了一臺實驗樣機，其參數見表1，控制算法采用DSP（型號為TMS320F2812）實現。實驗系統在圖4 所示的控制框圖基礎上增加負載電流前饋，并且增加相應的限幅環節。

圖10a～圖10c 左圖分別為系統空載、滿載（帶阻感負載，功率因數為0.75）和非線性負載（負載電流峰值達到額定負載電流峰值）時A相的輸出電壓和輸出電流波形，三者的穩態誤差分別為0.5V、0.8V 和2.2V；空載和阻感負載時系統具有很好的輸出波形；非線性負載時，輸出電流峰值約為61A，波峰因子為3.27，此時系統的THD 仍能限制在5%以內，可見系統對非線性負載具有很好的適應能力。圖10a～圖10c 右圖為三種工況下輸出電壓對應的THD 頻譜圖，其THD 值分別為1.28%、1.39%和3.25%，三者的主要諧波均為頻次較低的奇次諧波。圖10d 中，由于空載時系統阻尼減小，諧振峰處的諧波為0.3%左右，但并不影響系統的穩定性；圖10e 中，系統帶阻感性負載，由于死區引起的低次諧波隨功率因數的降低而增大，此時，5、7次諧波的幅值分別為0.85%和0.54%，均大于空載時對應次的諧波；圖10f為非線性負載時輸出電壓的THD 頻譜圖，由于本系統采用極點配置獲得了較高的系統帶寬，很好地抑制了由輸出電流引入的低次諧波（輸出電流的THD 接近90%，主要為5次和7次諧波），此時，輸出電壓中5次諧波為1.82%、7次諧波為1.71%，系統具有較強的波形控制能力。

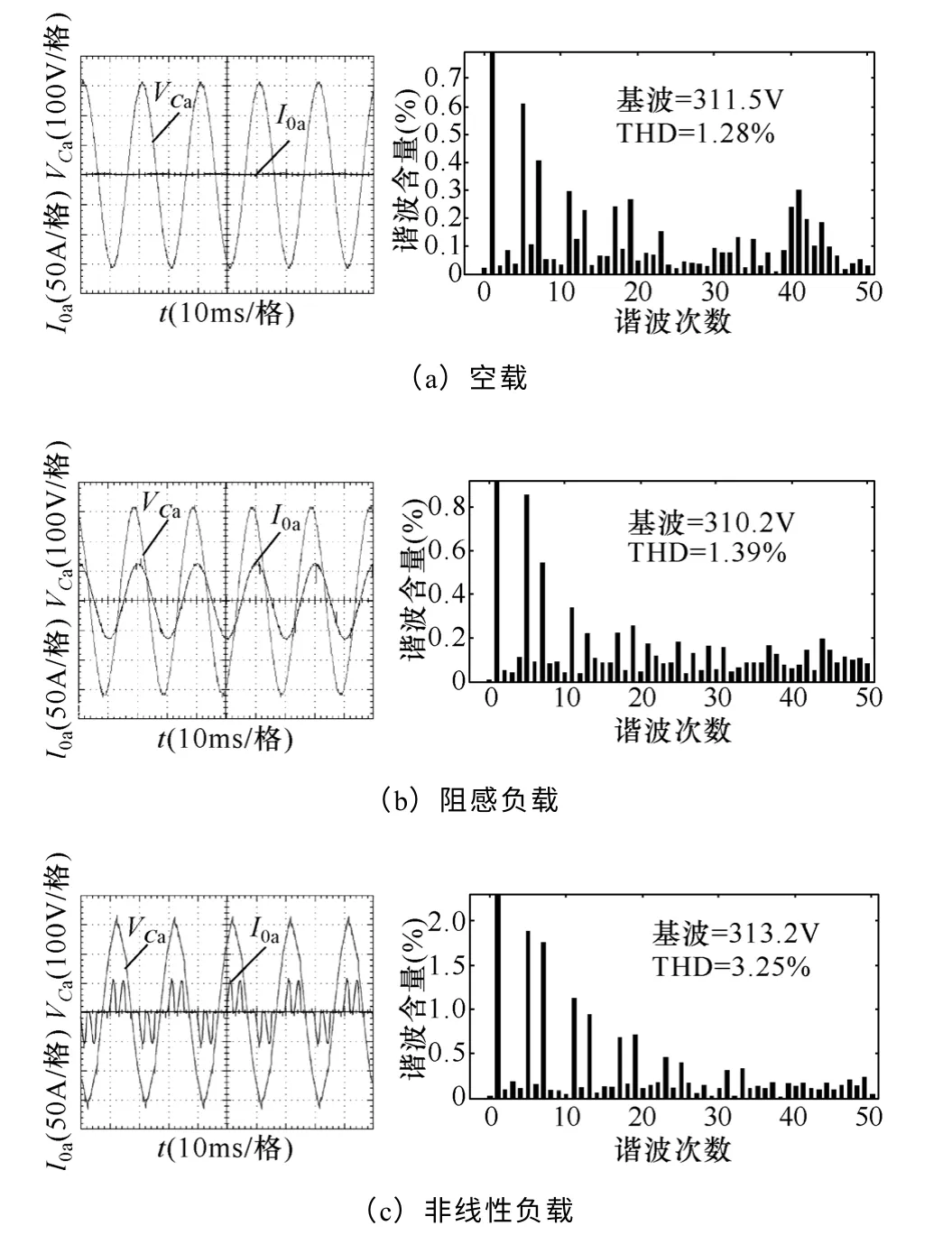
圖10 逆變器輸出電壓和電流波形及電壓THD 頻譜圖Fig.10 Output voltage and current waveforms and the corresponding THD spectrogram

圖11為系統突加突減負載時的實驗波形：圖11a 中，突加負載時輸出電壓超調約為8.2%，經過約2.5ms 的調節過程后恢復正常；圖11b為系統突卸負載時的輸出波形，由于實驗中采用交流斷路器切斷負載，負載電流下降有所減緩，此時卸載過程中輸出電壓基本沒有超調，調節時間小于2ms。可見，采用本文所述控制策略時，系統具有良好的動態特性。

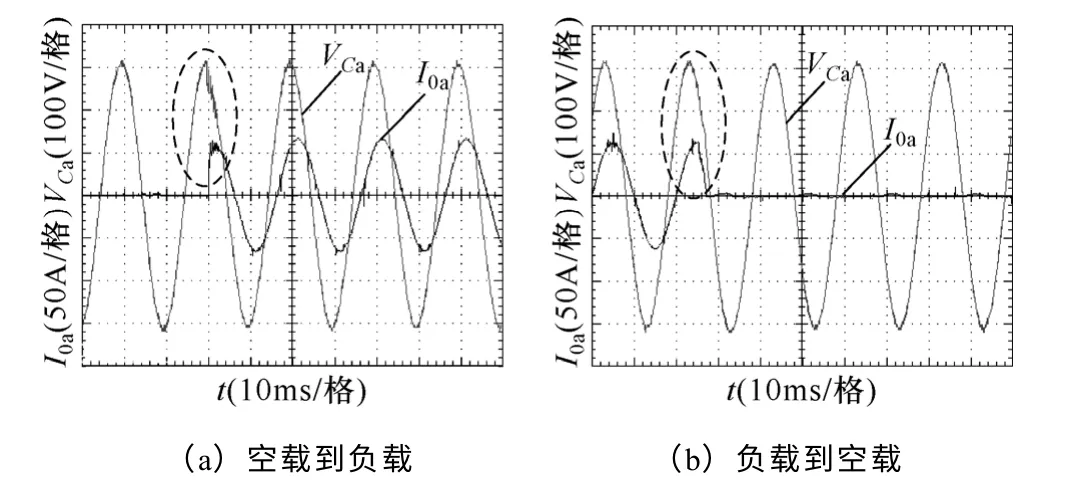
圖11 負載突變時輸出電壓和輸出電流波形Fig.11 Output voltage and current waveforms when load changing

5 結論

（1）分析了離散域下逆變器控制參數量與系統階數的關系，由于滯后一拍的引入使得逆變器離散域模型增加了一階，系統控制特性隨之變差，并且傳統的極點配置法將失效。

（2）通過引入控制器輸出量作為新的狀態變量，使得逆變器系統在離散域設計時實現了極點的任意配置，此時若系統采用雙環控制策略，則控制器可以選擇為P、PI、PD 或者PID 控制器。

（3）由于新增狀態變量來自控制系統內部，無需額外的傳感器和輔助算法，控制策略的實現非常簡單方便，且適用于單相和三相逆變器系統。

（4）仿真和實驗表明，采用本文所提控制策略，逆變器系統穩定可靠，同時具有良好的動態和靜態特性，特別適合于開關頻率低且需采用滯后一拍控制的大功率逆變電源系統。

[1]Carrasco J M,Franquelo L G,Bialasiewicz J T,et al.Power-electronic systems for the grid integration of renewable energy sources:a survey[J].IEEE Transactions on Industrial Electronics,2006,53(4):1002-1016.

[2]Vandoorn T L,Meersman B,Degroote L,et al.A control strategy for islanded microgrids with DC-link voltage control[J].IEEE Transactions on Power Delivery,2011,26(2):703-713.

[3]趙彪,于慶廣,王立雯,等.用于電池儲能系統并網的雙向可拓展變流器及其分布式控制策略[J].中國電機工程學報,2011,31(Sup.l):244-251.Zhao Biao,Yu Qingguang,Wang Liwen,et al.Bidirectional extensible converter and its distributed control strategy for battery energy storage gridconnected system[J].Proceedings of the CSEE,2011,31(Sup.l):244-251.

[4]郭衛農,陳堅.基于狀態觀測器的逆變器數字雙環控制技術研究[J].中國電機工程學報,2002,22(9):64-68.Guo Weinong,Chen Jian.Study on digital dual-loop control for inverters based on state-observer[J].Proceedings of the CSEE,2002,22(9):64-68.

[5]Ryan M J,Brumsickle W E,Lorenz R D.Control topology options for single-phase UPS inverters[J].IEEE Transactions on Industry Applications,1997,33(2):493-501.

[6]Ide T,Yokoyama T.A study of deadbeat control for three phase PWM inverter using FPGA based hardware controller[C].IEEE Power Electronics Specialists Conference,2004:50-53.

[7]Mattavelli P.An improved deadbeat control for UPS using disturbance observers[J].IEEE Transactions on Industrial Electronics,2005,52(1):206-212.

[8]Houari A,Renaudineau H,Martin J,et al.Flatness-Based Control of Three-Phase Inverter With Output LC Filter[J].IEEE Transactions on Industrial Electronics,2012,59(7):2890-2897.

[9]熊健,史鵬飛,張凱,等.基于積分環節電壓微分反饋的逆變器重復控制策略[J].電工技術學報,2007,22(1):85-90.Xiong Jian,Shi Pengfei,Zhang Kai,et al.Voltagedifferential-feedback with integral control plus repetitive control for PWM inverters[J].Transactions of China Electrotechnical Society,2007,22(1):85-90.

[10]Yokoyama T,Kawamura A.Disturbance observer based fully digital controlled PWM inverter for CVCF operation[J].IEEE Transactions on Power Electronics,1994,9(5):473-480.

[11]劉新民,鄒旭東,康勇,等.帶狀態觀測器的逆變器增廣狀態反饋控制和重復控制[J].電工技術學報.2007,22(1):91-95.Liu Xinmin,Zou Xudong,Kang Yong,et al.An inverter based on state-feedback integral control and repetitive control technology with state-observer[J].Transactions of China Electrotechnical Society,2007,22(1):93-98.

[12]Zhang K,Peng L,Kang Y,et al.State-feedback-withintegral control plus repetitive control for UPS inverters[C].IEEE Applied Power Electronics Conference and Exposition,2005:553-559.

[13]彭力.基于狀態空間理論的PWM 逆變電源控制技術研究[D].武漢:華中科技大學,2004.

[14]彭力,張凱,康勇,等.數字控制PWM 逆變器性能分析及改進[J].中國電機工程學報,2006,26(18):65-70.Peng Li,Zhang Kai,Kang Yong,et al.Performance analysis and improvement of digital controlled PWM inverter[J].Proceedings of the CSEE,2006,26(18):64-68.

[15]Mattavelli P,Polo F,Dal Lago F,et al.Analysis of control-delay reduction for the improvement of UPS voltage-loop bandwidth[J].IEEE Transactions on Industrial Electronics,2008,55(8):2903-2911.

[16]Deng H,Oruganti R,Srinivasan D.Adaptive digital control for UPS inverter applications with compensation of time delay[C].IEEE Applied Power Electronics Conference and Exposition,2004:450-455.

[17]孔雪娟.數字控制PWM 逆變電源關鍵技術研究[D].武漢:華中科技大學,2005.

[18]唐詩穎,彭力,康勇.脈寬調制逆變電源數字雙環控制技術研究[J].中國電機工程學報,2009,29(15):55-60.Tang Shiying,Peng Li,Kang Yong.Research on dual-loop digital control technique for pulse width modulation inverters[J].Proceedings of the CSEE,2009,29(15):55-60.