基于反推控制的永磁同步電動機速度的模糊控制

劉棟良 崔言飛 趙曉丹 陳鎂斌

（1.杭州電子科技大學自動化學院 杭州 310018 2.臥龍電氣集團有限公司 上虞 312300）

1 引言

永磁同步電機具有結構簡單、運行可靠、體積小、效率高、容易維護等優點，在伺服系統中得到了廣泛地應用。但是由于永磁同步電動機中轉速和電流的非線性耦合，使用一般線性控制方法難于達到控制性能的要求。為了實現對其有效控制，當前主要采用非線性控制方法有變結構控制[1,2]、微分幾何[3]和無源控制[4]等。但這些非線性控制的設計方法比較復雜，不易實現。

反推控制理論的提出在電機控制領域得到了廣泛的關注，并被應用于永磁同步電機伺服控制系統中[5]。反推控制是一種有效的非線性控制設計方法，它不但能夠實現永磁同步電動機系統的完全解耦，而且設計過程簡單。近年來，反推控制在永磁同步電動機系統中的應用取得了一些成果[6-8]。文獻[9]把反推控制策略應用于永磁同步電動機速度的跟蹤系統中，簡化了一般系統設計過程，減少了系統控制中的調節參數數目，保證了系統具有全局穩定性，并實現了良好的速度跟蹤，但它沒有考慮系統中參數的變化對系統性能帶來的影響。文獻[10]采用自適應控制與狀態反饋精確線性化控制相結合，所給出的控制器設計是建立在電機角速度與電流乘積項基礎上，使控制器的設計難度大大增加。文獻[11]提出了自適應控制與反推控制相結合應用于具有不確定參數的永磁同步電機速度跟蹤系統中，該方法針對控制系統中電阻和負載的實時估計，在一定程度上實現了對擾動的抑制，但它沒有考慮系統的速度和電流反推調節器中反推參數對系統性能的影響。由于系統設計中參數的選取對系統穩定性和動態性能有很大影響，因此永磁同步電動機調速系統中，反推調節器中速度和電流的反推參數的選取十分重要。

針對上述問題，本文提出了把模糊反推控制應用于永磁同步電動機的速度控制系統中，通過模糊原理設計出模糊控制器，根據設定的模糊規則對反推參數進行實時調節，優化參數。采用模糊反推控制不但實現了永磁同步電動機系統的完全解耦，而且能夠增強系統抗干擾性，實現快速的速度跟蹤。Matlab 仿真和實驗結果表明，通過模糊控制器對反推控制參數的在線修正，大大提高了系統的靜態和動態性能，保證了系統的全局的穩定性，并使系統具有較強的魯棒性。

2 永磁同步電機數學模型

基于同步旋轉轉子dq 坐標下的表面式的永磁同步電動機的定子電壓[12]如下：（其交直軸電感近似相等，即Ld=Lq=L）

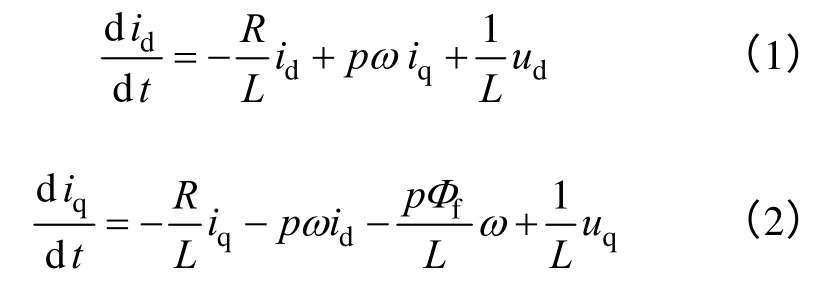
式中 ud，uq——d、q 軸定子電壓；

id，iq——d、q 軸定子電流；

R——定子電阻；

Φf——永磁磁通；

L——定子電感；

p——極對數；

J——轉動慣量；

B——粘滯摩擦系數；

TL——負載轉矩；

ω——轉子機械角速度。

3 系統控制的設計

3.1 反推控制設計

反推設計過程是逐步遞推的設計過程。該過程中引進了虛擬狀態和虛擬控制函數，前面的子系統必須通過后面子系統的虛擬控制才能達到目的。它是通過從原系統方程中選取狀態構造新的子系統，并構造Lyapunov 函數，設計虛擬控制函數，使子系統穩定，然后逐步設計，直到得到系統實際控制，保證整個系統穩定[13]。

在永磁同步電動機控制系統中，為了實現電機實際轉速跟蹤期望的參考轉速，需要利用反推控制理論，設計反推控制器。反推控制器的設計過程參考文獻[9]。

在設計過程中，首先，選擇速度的跟蹤誤差e為系統的狀態變量，為了實現速度的全局漸進跟蹤，構造Lyapunov 函數，并根Lyapunov 據穩定判據，引入了虛擬電流控制函數為

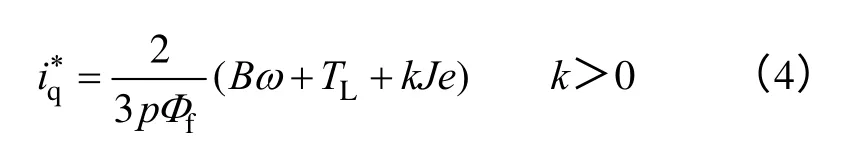
然后，為了實現對虛擬參考電流的跟蹤，選擇電流跟蹤誤差ed、eq為虛擬誤差變量

由e、ed、eq構成新的子系統，為了實現電流對參考電流的跟蹤，構造新的子系統的Lyapunov 函數，并由穩定判據，得到系統實際控制量uq和ud為

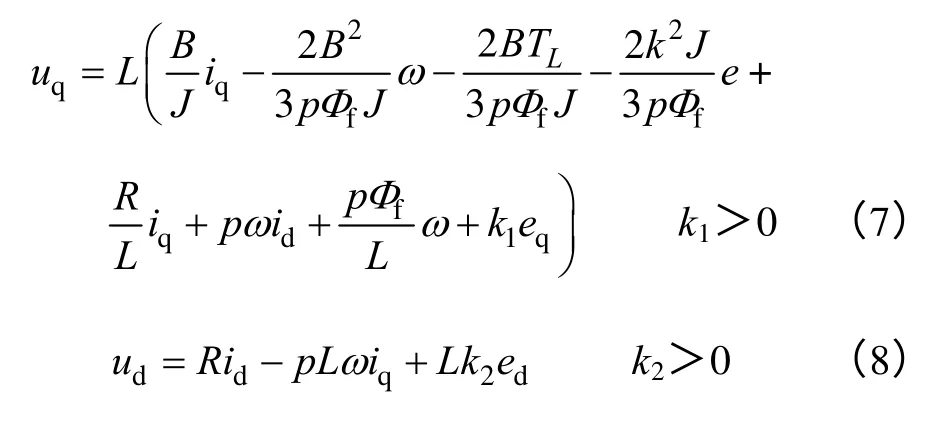
通過式（7）和式（8）便得到了系統的實際控制量。

由式（4）設計的速度環的反推控制器，式（7）和式（8）設計的電流環的反推控制器，不但能夠使得永磁同步電動機系統達到速度的漸近跟蹤，同時電流的穩定跟蹤能夠使得系統具有快速的響應速度。

3.2 模糊控制器的設計

根據反推控制器的設計，可知永磁同步電動機系統的反推控制調節參數有三個，即速度ω 調節參數k，轉矩電流iq的調節參數k1和磁通電流id調節參數k2。為了使系統達到快速的速度跟蹤和較強的魯棒性，不但要求反推控制參數k＞0，k1＞0，k2＞0，還需要根據系統不同運行狀態調節k，k1，k2數值。通過大量仿真證明k2的取值變化對系統運行狀態影響極小，其變化可以不考慮，因此只需要保證滿足系統穩定條件，即k2＞0。所以本控制系統只需要調節的參數只有k 和k1。本文通過模糊控制器的設計[14-16]，對反推控制參數進行優化處理，使系統實現較強的伺服性能。

系統設計的模糊控制器是以速度偏差e 和偏差變化率ec為輸入量，反推參數修正值Δk、Δk1為輸出量。先找出參數k、k1與e 和ec之間的模糊關系，在運行中不斷檢測e 和ec，再根據模糊控制原理對參數k、k1進行在線修改，以滿足在不同e 和ec時對參數k 和k1的不同要求。

通過大量測試，得出在不同e 和ec下被控過程對參數k、k1的整定要求，總結以下規律：

（1）當|e|較大時，為了使系統有較好的可快速跟蹤性能，應取較大k 和較小的k1。

（2）當|e|中等時，為了減小系統超調，應取較小k 和較大的k1。

（3）當|e|較小時，為了使系統有較好的穩態性能和抗干擾能力，應取較大的k 和適當的k1。

設計模糊控制器時，首先需要確定輸入與輸出變量的模糊子集合的論域和隸屬函數。由于模糊控制器的輸入、輸出變量都是精確量，而模糊推理是針對模糊量進行的，所以需要先對輸入變量進行模糊化。定義輸入變量e、ec和輸出變量Δk、Δk1的模糊集論域均為[-4 4]，輸入、輸出變量模糊子集均為{NB NS ZO PS PB}，且其隸屬函數采用三角形函數，如圖1 所示，由此可得到模糊子集的隸屬度。

圖1 輸入和輸出隸屬函數圖Fig.1 Input and output membership functions diagram

模糊控制器根據被控對象的狀態自動調整輸出變量Δk、Δk1的值，并對反推參數進行在線校正，計算公式為

根據應用經驗和前面總結規律，確定兩個輸出量與輸入量的模糊控制規則分別見表1 和表2。模糊推理采用Mandani 型模糊推理算法。

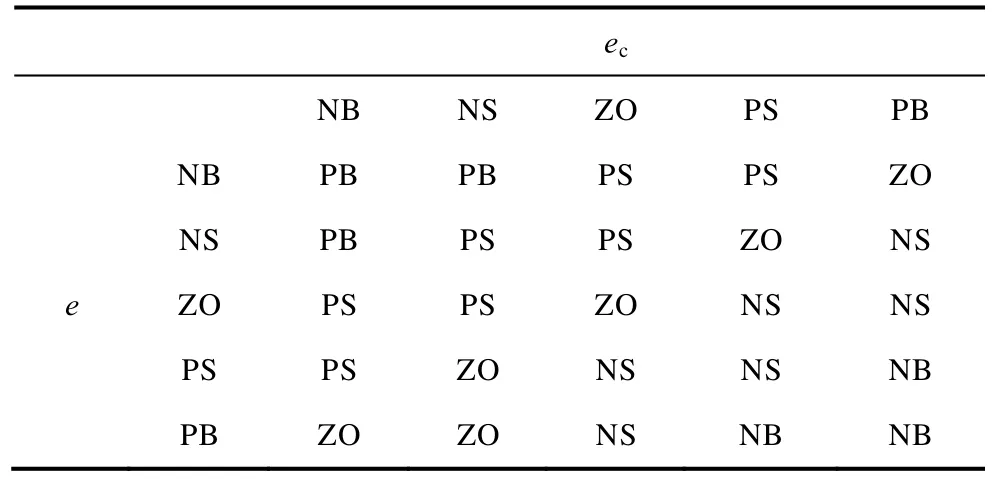
表1 Δk 的模糊規則表Tab.1 Fuzzy rule table of Δk

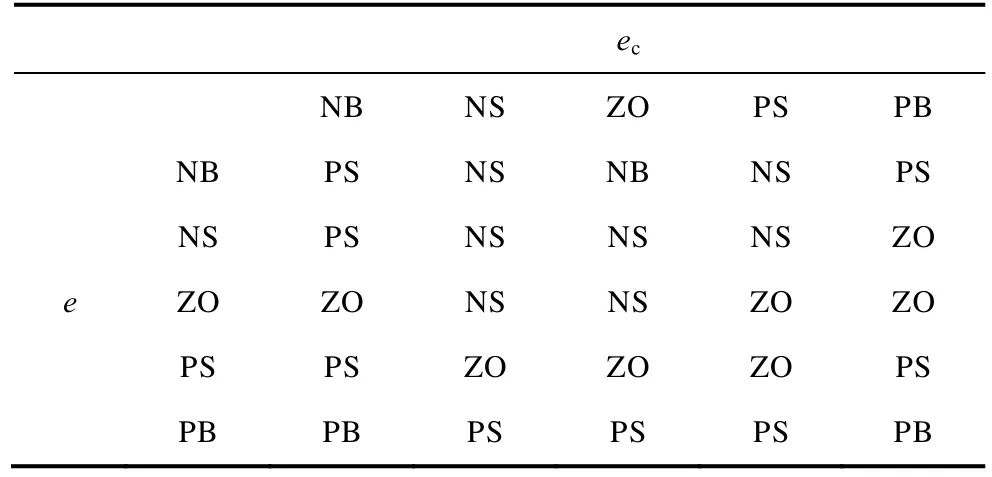
表2 Δk1的模糊規則表Tab.2 Fuzzy rule table of Δk1

根據Mandani 模糊推理方法，模糊控制的輸出曲面如圖2 和圖3 所示。

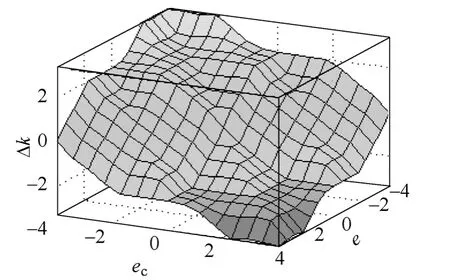
圖2 Δk 的模糊推理輸出曲面Fig.2 Fuzzy reasoning output surface of Δk

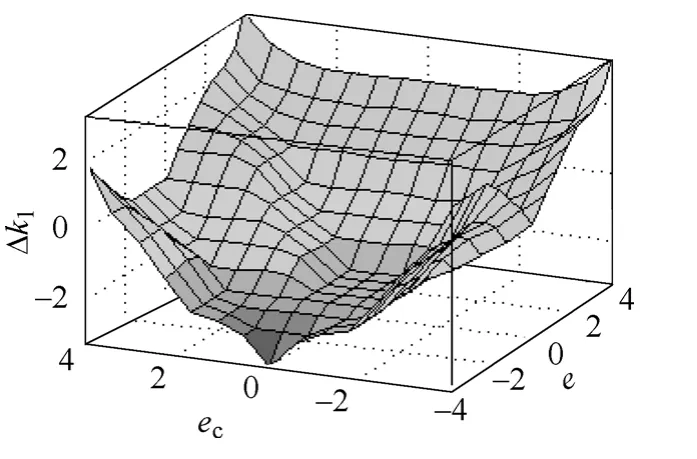
圖3 Δk1的模糊推理輸出曲面Fig.3 Fuzzy reasoning output surface of Δk1

經模糊推理后，模糊控制輸出為模糊量，不能直接用于控制對象，還需對模糊量要進行去模糊化，并將其轉換到控制對象所能接受的基本論域中去，去模糊化處理采用重心法。

4 系統仿真與實驗結果

4.1 仿真實驗

圖4 所示為永磁同步電動機系統的模糊反推控制結構框圖。用于仿真的1kW 的永磁同步電動機參數為：極對數p=4，轉動慣量J=0.001kg·m2，永磁磁通Φf=0.8Wb，粘滯摩擦系數B=0.000 1，定子電感L=0.006H，定子電阻R=2Ω。

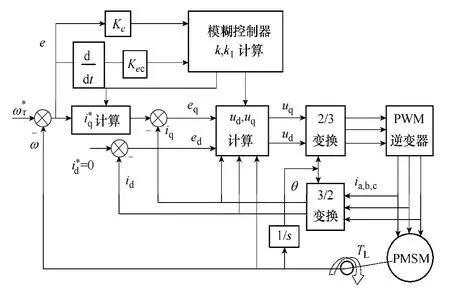
圖4 PMSM 的模糊反推控制系統框圖Fig.4 Fuzzy backstepping control diagram of PMSM

設定電動機的初始跟蹤速度為300r/min，初始負載為零，在0.4s 時突加負載5N·m，在0.7s 時負載降為0N·m。仿真中反推參數初始值取為：

當電動機給定參數發生變化時，在沒有模糊控制環節的情況下，反推控制系統仿真結果如圖5所示，圖5a為轉速變化波形，圖5b為轉矩變化波形，圖5c為三相定子電流變化波形。模糊反推控制系統仿真結果如圖6 所示，圖6a為轉速變化波形，圖6b為轉矩變化波形，圖6c為三相定子電流變化波形。

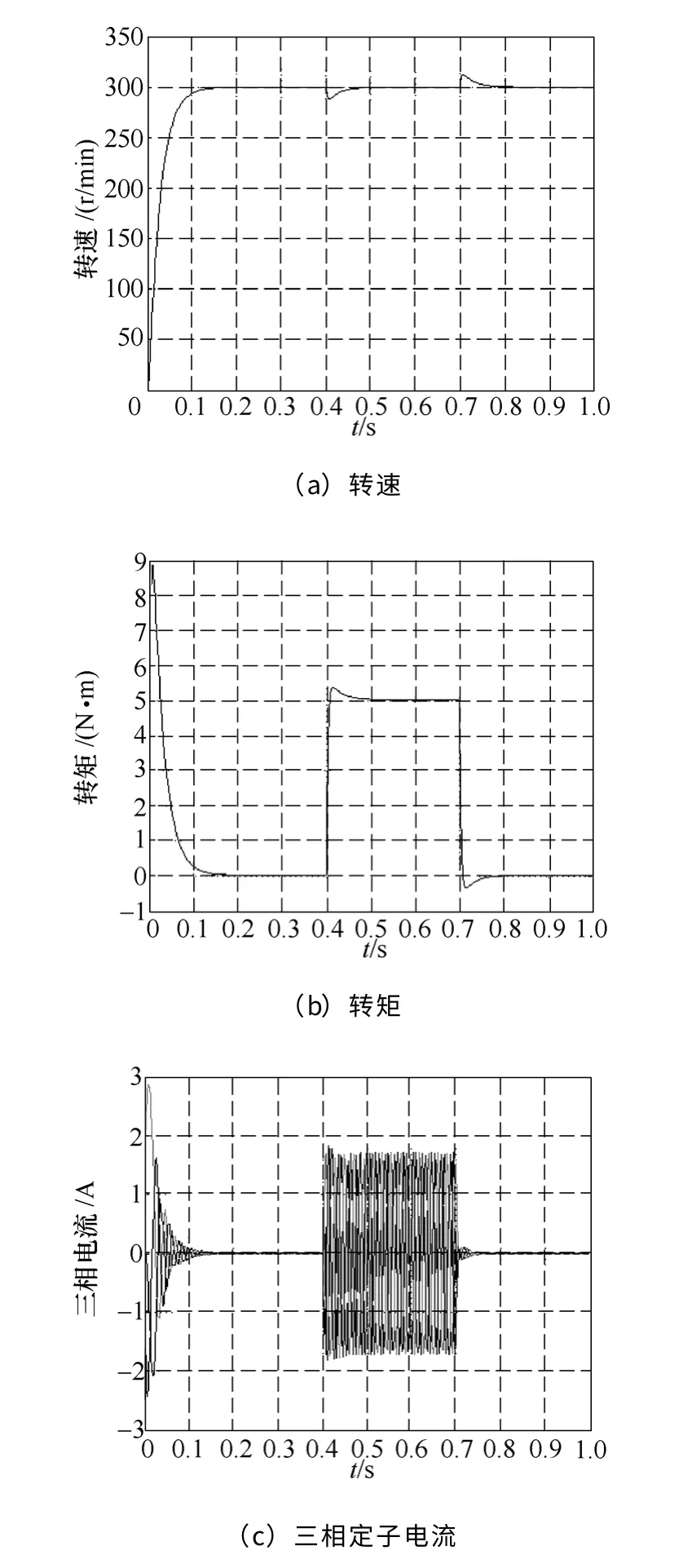
圖5 反推控制的仿真結果Fig.5 Transient responses with backstepping control by simulation

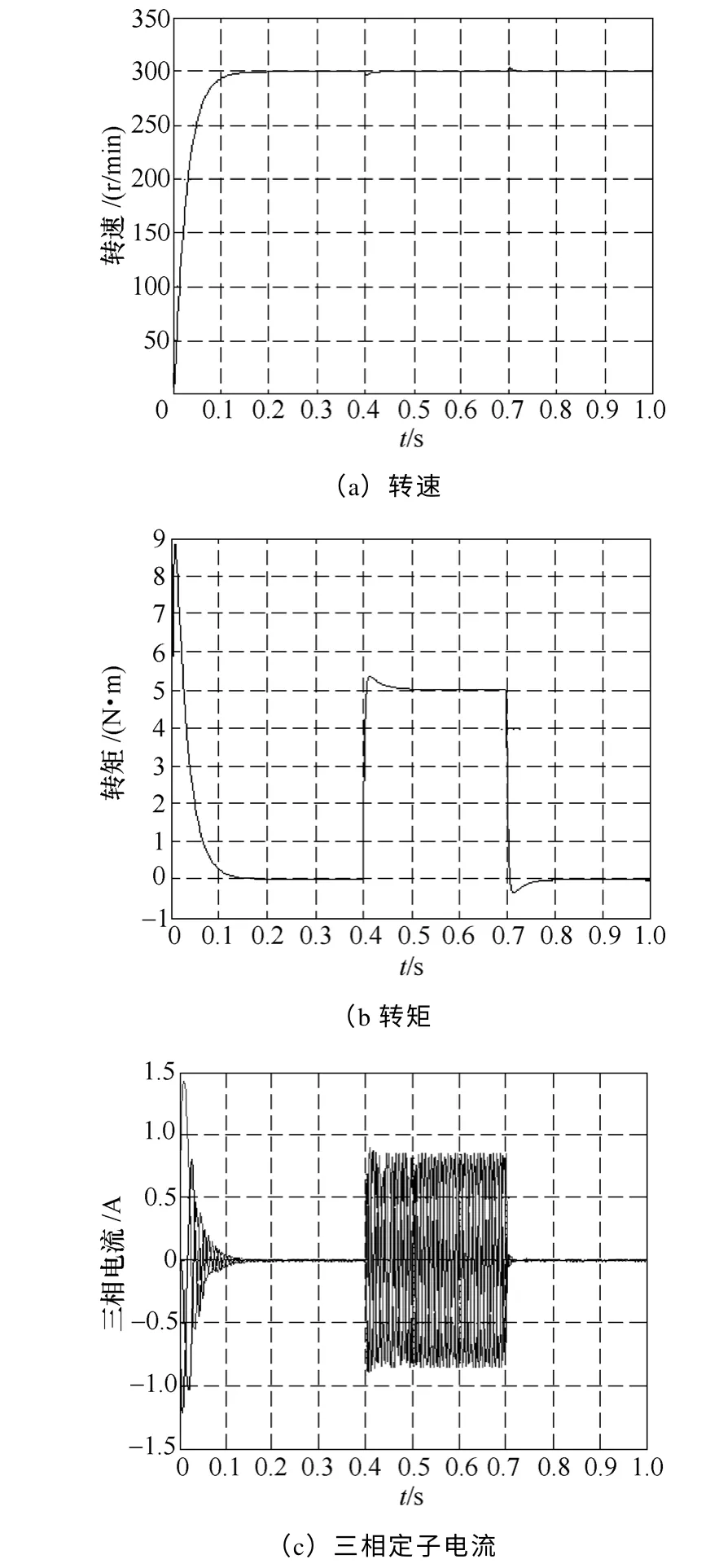
圖6 模糊反推控制仿真結果Fig.6 Transient responses with fuzzy backstepping control by simulation

由仿真結果可以看出，當系統負載發生變化時，與反推控制策略相比，模糊反推控制策略通過模糊控制器對反推參數k、k1的實時調節，使速度的超調量與調整時間明顯降低，三相電流波動減小，系統響應快速平穩。使系統具有快速的速度跟蹤和抗干擾能力強的特性，動、靜態性能都要優于反推控制。

4.2 實驗結果

為了驗證所提控制策略的有效性和可行性，在交流伺服系統的實驗平臺上進行了實驗研究。實驗系統采用TI 公司的TMS320F28034 芯片為核心，采用磁粉制動器給定電機負載，電機轉速值通過D-A數模轉換過來，并通過Tektronix TDS 2014B 示波器顯示，實驗裝置如圖7 所示。

圖7 實驗平臺Fig.7 Experiment system

實驗是通過系統負載變動，對采用反推控制和模糊反推控制兩種控制策略的系統響應進行對比。圖8 所示為無模糊控制的反推控制策略下的轉速和定子電流波形，電機轉速設定為300r/min，空載起動運行至穩定，實驗中電動機首先突加5N·m 負載然后突卸5N·m 負載，圖8a是轉速波形，突加和突卸負載時轉速波動值對應速度為12.4r/min，負載變動過程中轉速出現最大誤差為4.1%；圖8b為此過程中三相電流波形，如圖中標注圓，在突加負載和突卸負載過程中時有明顯的波動。圖9是相同實驗條件下，采用模糊反推控制策略的速度和定子電流波形，圖9a是轉速波形，負載變動中轉速最大波動值對應速度為3.9r/min，誤差為1.3%；圖9b為此過程中三相電流波形，如圖中標注圓，在突加負載和突卸負載時沒有明顯波動。

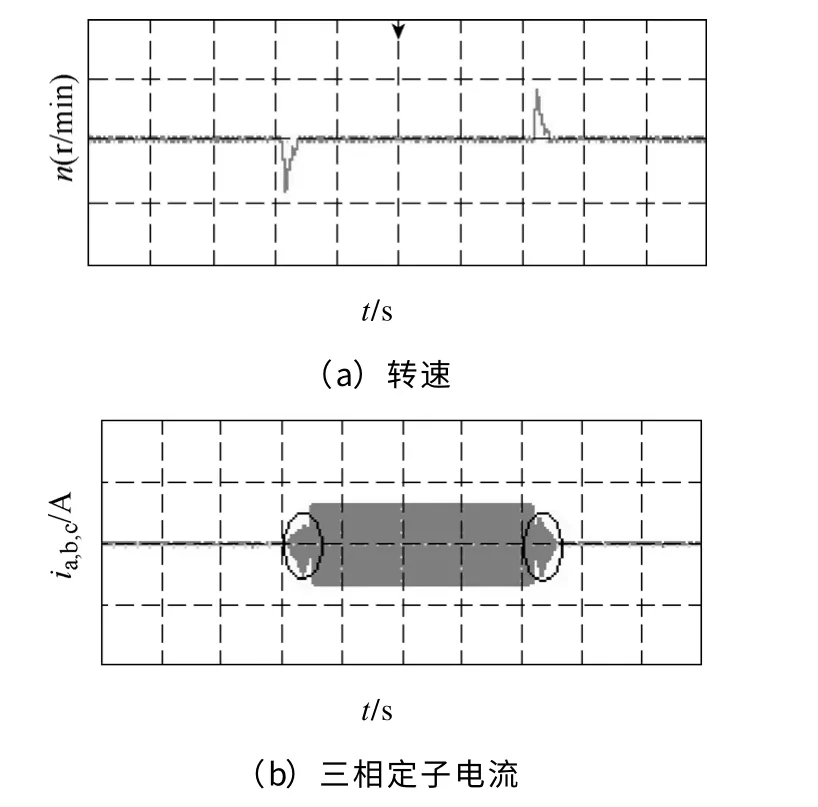
圖8 無模糊反推控制實驗結果Fig.8 Experimental results with backstepping control

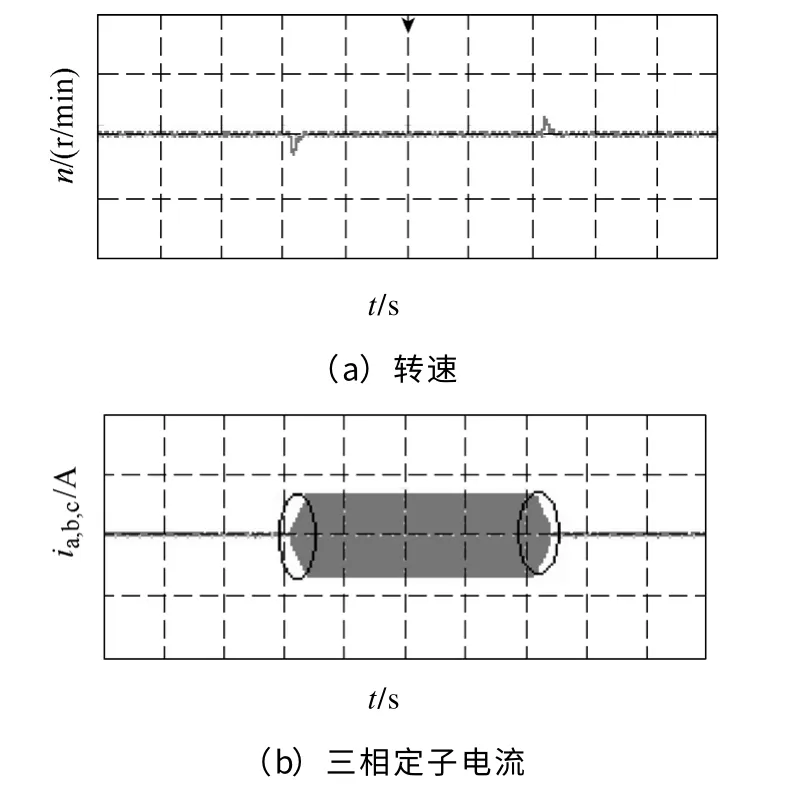
圖9 模糊反推控制實驗結果Fig.9 Experimental results with fuzzy backstepping control

由圖8a 和圖9a 可以看出，系統在兩種控制策略下，當負載轉矩發生變化時，選擇模糊反推控制其轉速波動小、調節時間短，速度跟蹤效果更好，速度實驗波形與仿真圖5a、圖6a 波形結果基本一致。由圖8b 和圖9b 可以看出，選擇模糊反推控制在突加和突卸負載時，其電流變化平穩，基本沒有調節過程，表明系統對轉矩擾動有明顯的抑制作用。

5 結論

本文把模糊控制和反推控制相結合應用于永磁同步電動機速度跟蹤中。該方法通過模糊控制器對反推參數的在線調節，在保證系統全局漸近穩定的同時，實現了速度的快速跟蹤性和較強的魯棒性，使系統在動態和穩態時都能達到較高的控制精度。仿真和實驗結果表明了該方法是有效性，把模糊反推控制應用于交流伺服系統中，能夠實現良好的伺服性能。

[1]Baik I,Kin K,Youn M.Robust nonlinear speed control of PM synchronous motor using boundary layer integral sliding mode control technique[J].IEEE Transactions on Control Systems Technology,2000,8(1):47-54.

[2]張曉光,趙克,孫力,等.永磁同步電動機滑模變結構調速系統新型趨近率控制[J].中國電機工程學報,2011,31(24):77-82.Zhang Xiaoguang,Zhao Ke,Sun Li,et al.A PMSM sliding mode control system based on a novel reaching law[J].Proceedings of the CSEE,2011,31(24):77-82.

[3]任元,孫玉坤,劉葉飛,等.基于微分幾何方法的永磁同步電動機變結構控制[J].微特電機,2006,34(11):33-35,39.Ren Yuan,Sun Yukun,Liu Yefei,et al.Variable structure control in permanent magnet synchronous motor based on the differential geometry method[J].Small &Special Electrical Machines,2006,34(11):33-35,39.

[4]Orgega R,Nicklasson P J,Espinosa G.Passivitybased control of the general rotating electrical machines[C].Proceedings of IEEE Conference on Decision and Control,1994:4018-4023.

[5]劉棟良,王家軍,趙光宙,等.永磁同步電動機調速中的反推控制[J].電氣傳動,2005,35(6):39-41.Liu Dongliang,Wang Jiajun,Zhao Guangzhou,et al.Backstepping control and its application of PMSM[J].Electric Drive,2005,35(6):39-41.

[6]Hu Jianhui,Xu Yongxiang,Zou Jibin.Design and implementation of adaptive backstepping speed control for permanent magnet synchronous motor[C].Proceedings of the 6th World Congress on Intelligent Control and Automation,2006:2011-2015.

[7]王家軍,王建中,馬國進.感應電動機系統的變結構反推控制研究[J].中國電機工程學報,2007,27(6):35-38.Wang Jiajun,Wang Jianzhong,Ma Guojin.Variable structure control with backstepping of induction motor system[J].Proceedings of the CSEE,2007,27(6):35-38.

[8]劉棟良,鄭謝輝,崔麗麗.無速度傳感器永磁同步電機反推控制[J].電工技術學報,2011,26(9):67-72.Liu Dongliang,Zheng Xiehui,Cui Lili.Backstepping control of speed sensorless permanent magnet synchronous motor[J].Transactions of China Electrotechnical Society,2011,26(9):67-72.

[9]王家軍,趙光宙,齊冬蓮.反推式控制在永磁同步電動機速度跟蹤控制中的應用[J].中國電機工程學報,2004,24(8):95-98.Wang Jiajun,Zhao Guangzhou,Qi Donglian.Speed tracking control of permanent magnet synchronous motor with backstepping[J].Proceedings of the CSEE,2004,24(8):95-98.

[10]高春能,紀志成.永磁同步電機的模型參考模糊自適應控制[J].系統仿真學報,2008,20(7):1817-1820.Gao Chunneng,Ji Zhicheng.Model reference fuzzy adaptive control of permanent magnet synchronous motor[J].Journal of System Simulation,2008,20(7):1817-1820.

[11]劉棟良,王家軍,崔麗麗.永磁同步電機參數自適應調速控制[J].電工技術學報,2011,26(8):159-165.Liu Dongliang,Wang Jiajun,Cui Lili.Speed tracking control of permanent synchronous motors with adaptive parameters[J].Transactions of China Electrotechnical Society,2011,26(8):159-165.

[12]Pragasen Pillay,Krishnan R.Modeling of permanent magnet motor drives[J].IEEE Transactions on Industry Electronics,1988,35(4):537-541.

[13]Wang J J,Zhao G Z,Qiu J,et al.Position tracking control of permanent magnet synchronous motor servo system[C].Proceedings of the 5th World Congress on Intelligent Control and Automation,Hangzhou,2004:4512-4515.

[14]Sun Hua,Yuehong Dai.Fuzzy PID control and simulation experiment on permanent magnet linear synchronous motors[C].Electrical and Control Engineering,2010:1047-1049.

[15]Yu Junzhi,Hu Xiaolei,Ding Rui.Fuzzy logic PID based control design for permanent magnet synchronous motor servo system[J].Intelligent Computation Technology and Automation,2009,2(2):728-731.

[16]曾光齊,胡均安,王東,等.模糊控制理論與工程應用[M].武漢:華中科技大學出版社,2006.