無軸承異步電機動不平衡振動補償控制

詹立新 周 凱

（清華大學機械工程系 北京 100084）

1 引言

無軸承電機是一種將磁軸承和電機融合為一體的新型電機形式。與傳統磁懸浮電機機理不同，它利用磁軸承定子結構與交流電機定子結構的相似性，將轉矩繞組和懸浮繞組一起繞進電機定子[1,2]。電機的磁懸浮控制以轉矩繞組提供的氣隙磁場為偏置磁場，通過調制懸浮繞組電流來調制電機轉子所受的磁懸浮力，從而達到讓電機轉子懸浮運轉的效果。無軸承電機運行時無機械接觸，適合應用于高速及超高速運轉場合，因而在機床電主軸、高速離心設備、渦輪分子泵、飛輪儲能等領域具有重要的研究價值和應用前景[3]。目前，有關學者已經提出了若干種類型的無軸承電機，如感應型、表貼永磁型、內插永磁型、內埋永磁型，交替極型、同極型、混合極型以及同步磁阻和開關磁阻型等[3]。其中，籠型無軸承異步電機以其結構簡單、可靠性高、易于弱磁以及能夠產生較大懸浮力[4]等特點，成為開展研究最早、最為廣泛的類型之一。

然而，對無軸承電機轉子來說，即使加工精度非常高，仍然不可避免地存在質量偏心。旋轉時由于轉子質量偏心產生的離心力與轉速的平方成正比，因此即使是非常小的偏心量，也會在高速旋轉機械中產生很大的離心力，導致不平衡振動，從而影響懸浮的精度和品質。一方面，由于質量不平衡產生的電磁振動力會經過氣隙傳遞給機座，產生噪聲，同時振動還會影響電機系統的運行性能，使無軸承電機轉速進一步提升受到限制；另一方面，由于位移傳感器檢測到的信號為振動信號，此振動信號經位移負反饋送入控制器，會導致功率放大器的電流飽和，這就對功放要求較高，同時電流增大嚴重時還會燒毀整個控制回路。所以，能否有效克服無軸承電機轉子的周期性離心力影響，將是無軸承電機能否在超高速領域廣泛應用的關鍵之一。

目前，磁軸承的不平衡補償研究已經經歷了二十多年的時間，相關學者結合了許多控制理論方法，提出了很多種不平衡振動補償策略[5-13]。這些方法大致可以分為兩類：

（1）電流最小控制。在一定的轉速下減小轉子的剛度和阻尼，使轉子圍繞其慣性軸旋轉，從而減小或消除振動力，此時功放中的控制電流振蕩最小。這個策略的優點是，由于轉子的偏心不會很大，只要保證氣隙足夠大，總可以使振動力無法傳遞到基座上。但是由于這種控制策略要求轉子剛度較小，故不能應用到高精度的場合，這也是限制其發展的一大缺點。

（2）位移最小控制。在一定轉速下，增加懸浮轉子的剛度和阻尼，使轉子圍繞其幾何中心旋轉，從而達到減小和消除振動的目的。這一策略具有高精度、高阻尼的特點，因而應用于對轉子旋轉精度要求較高的場合，但是有振動力產生，因此不能完全阻止定子和機座的振動[14]。

無軸承電機雖和磁軸承電機存在某些相似性，但其懸浮運行控制方法仍有很大的差別，無軸承電機控制更為復雜。針對無軸承電機周期性旋轉慣性振動控制方面的研究成果還很少見到。文獻[15]提出了基于前饋補償控制器的無軸承永磁同步電機轉子質量不平衡補償方案，推導了存在質量不平衡時的轉子運動方程，但是沒有得出閉環控制下無軸承電機轉子的運動軌跡方程；其以轉子振動信號作為補償信號，只是對周期性振動的開環補償，且文中僅進行了仿真實驗研究。文獻[16]提出了一種應用于無軸承開關磁阻電機的基于最小均方算法（LMS）的自適應凹陷濾波器的轉子質量偏心補償控制方案，其實現了電流最小控制，使轉子繞其慣量軸旋轉，從而達到消除不平衡振動力的目的，但文中并未對無軸承開關磁阻電機的位移最小控制進行研究。

針對上述問題，本文提出了一種基于前饋控制的無軸承異步電機動不平衡閉環補償控制策略，通過在無軸承異步電機原有的懸浮控制系統上加上一個前饋控制，利用控制器產生一定的控制力來補償轉子不平衡離心力，強行約束轉子圍繞其幾何中心軸旋轉，從而達到轉子振動位移最小的目的。該方法能夠將轉子的渦動半徑控制到很小的范圍，因而可以應用于對轉子的旋轉精度要求較高的場合。此外，本文闡述了無軸承異步電機不平衡振動的機理，并推導了存在質量偏心時無軸承異步電機徑向位移環僅采用PID 控制下的轉子運動學方程。最后，搭建了無軸承異步電機實驗平臺，實驗結果表明所提出方法很好地抑制了無軸承異步電機不平衡振動，取得了較好的動態懸浮控制效果。

2 無軸承異步電機懸浮機理及數學模型

2.1 無軸承異步電機懸浮機理

本文所述的無軸承異步電機在電機的定子中嵌入了兩套具有不同極對數的繞組，其中一套是四極轉矩控制繞組，另一套是兩極懸浮控制繞組。圖1所示為無軸承異步電機懸浮機理示意圖。

圖1 無軸承異步電機懸浮機理Fig.1 Principle of bearingless induction motor

設與電機定子同軸的靜止坐標系為xy 坐標系，且兩套繞組的αβ 坐標系重合，并與xy 坐標系重合。如圖1 所示，四極轉矩繞組氣隙磁場ψ1由勵磁電流i1m產生，在沒有負載的情況下，轉子將位于中心位置，此時氣隙中每一處的磁場強度都是相同的，即轉子處于受力平衡的狀態。如圖1 所示，當兩極懸浮繞組通以β 軸氣隙磁場勵磁電流im2β時，區域3中氣隙磁場的強度將增大，區域4 中氣隙磁場的強度將減弱，而區域1 和2 的氣隙磁場強度依然相等。因此，轉子所受麥克斯韋力的合力應朝向y 正方向。懸浮繞組通以反向的β 軸氣隙磁場勵磁電流則會產生y 負向的麥克斯韋力。同理，x 方向的懸浮力可通過懸浮繞組α 軸氣隙磁場勵磁電流im2α產生。因此，在懸浮繞組中分別通以α 軸和β 軸氣隙磁場勵磁電流，即可實現對無軸承異步電機轉子xy 坐標系下懸浮力的控制。

2.2 無軸承異步電機數學模型

對于本文研究的無軸承異步電機，當轉矩繞組采用矢量控制方式時，轉子所受懸浮力可寫成[17,18]

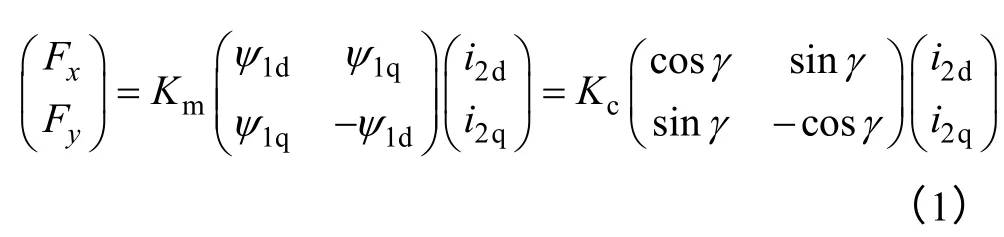
式中 r，l——轉子半徑和長度；

Lm2——懸浮繞組互感；

N1，N2——轉矩繞組和懸浮繞組繞線匝數；

μ0——空氣磁導率，μ0=4π×10-7；

ψ1d，ψ1q——轉矩繞組氣隙磁鏈在dq 坐標系下的分量；

γ——轉矩繞組氣隙磁場在dq 坐標系下的相角度，γ=arctan(ψ1q/ψ1d)；

i2d，i2q—— 懸浮繞組氣隙磁場勵磁電流在dq 軸下的分量；

Kc——力電流系數，Kc=Kmψ1m；

ψ1m——轉矩繞組氣隙磁鏈值，

將式（1）變換到αβ 坐標系下，有

式中 im2α，im2β——懸浮繞組氣隙磁場勵磁電流在αβ 軸的分量；

θ2——轉矩繞組氣隙磁鏈相位角，θ2=θ1+γ，θ1為轉矩繞組定子電流矢量逆時針方向的電角度。

考慮到無軸承異步電機轉矩繞組和懸浮繞組都會在籠型轉子上產生感應電流，而懸浮繞組在轉子上產生的感應電流會導致懸浮繞組氣隙磁場勵磁電流矢量i2m并不等于懸浮繞組中實際電流矢量i2s，而是存在一個相位延遲[19,20]。設該相位差為φi，則在αβ 坐標系下有

將式（3）代入式（2），可得實際產生的懸浮力為

從式（4）可以看出，由于懸浮繞組氣隙磁場勵磁電流和其實際電流之間存在相位差φi，導致實際產生的懸浮力和原懸浮力指令之間也存在一個相位延遲；該相位延遲會導致實際控制懸浮力在xy 方向上的相互耦合。此外，φi會隨著電機轉速的增大而增大。由于該相位延遲的存在會導致整個懸浮閉環控制系統相位裕度減小，當轉速增大到一定值時有可能會導致整個懸浮控制系統失穩。因此，在實際的懸浮繞組反饋閉環控制系統中，除了需要獲取轉矩繞組氣隙磁鏈相位角，為了使系統穩定運行，還應對產生的懸浮力指令進行相位超前補償。如何獲取φi可以詳細參見文獻[19,20]。

以下為了簡化分析，不妨令ix和iy為懸浮繞組反饋控制系統指令電流，且有

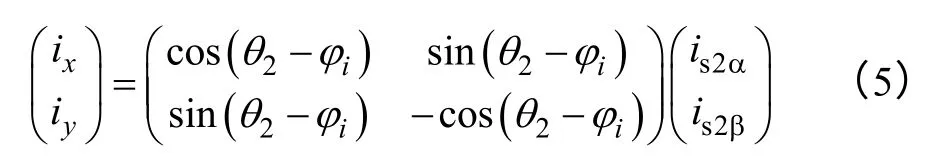
則由式（4）、式（5）可得

在轉子存在偏心情況下，除上述可控懸浮力外，還存在由偏心引起的單邊磁拉力，其表達式為

式中 Ke——力位移系數，

δ0——電機氣隙長度。

因此，在轉子存在偏心的情況下，無軸承異步電機轉子所受的電磁力為

無軸承異步電機單個方向運動的動力學模型如圖2 所示，如圖所示，x 方向給定位移量同檢測到的實際位移量比較，其差值通過PID 位移調節器產生懸浮可控磁懸浮力指令Fx*，用于克服單邊磁拉力和外力。圖2 中，Fwx為無軸承異步電機所受外力，其中一階時間延遲環節表示可控磁懸浮力延遲，主要由數字控制器的采樣周期、電流調制延遲以及定轉子鐵心中存在電渦流等因素引起。

圖2 無軸承異步電機動力學模型Fig.2 Dynamic model of bearingless induction motor

3 質量偏心引起的不平衡振動機理分析

如圖2 所示，無軸承異步電機轉子的運動方程為

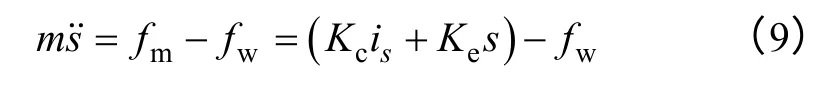
式中 m——轉子質量；

fm——電磁力；

fw——轉子在運動方向上所承受的外力（包括轉子自重和負載）；

s——某個方向（x 向或y 向）的位移；

is——對應方向的懸浮繞組控制電流。

當轉子存在質量偏心時，如圖3 所示，轉子幾何中心為Og，轉子質心為Om，轉子幾何中心處于以定子中心為中心的xy 坐標系下的坐標為（x,y）。存在質量偏心時無軸承異步電機x 方向運動的動力學模型如圖4 所示。

圖3 無軸承異步電機轉子質量不平衡示意圖Fig.3 Diagram of mass imbalance of the bearingless induction motor rotor

圖4 存在質量偏心時無軸承異步電機轉子動力學模型Fig.4 Dynamic model of the bearingless induction motor with mass imbalance

如圖3 所示，設轉子質心偏離轉子幾何中心的距離為ε，當電機轉子以ωr角速度運轉時，由質量偏心引起的不平衡離心力為

式中，ξ為初始狀態下轉子質心偏離轉子幾何中心的相角。

在考慮轉子存在質量偏心的情況下，轉子的運動方程可以寫成

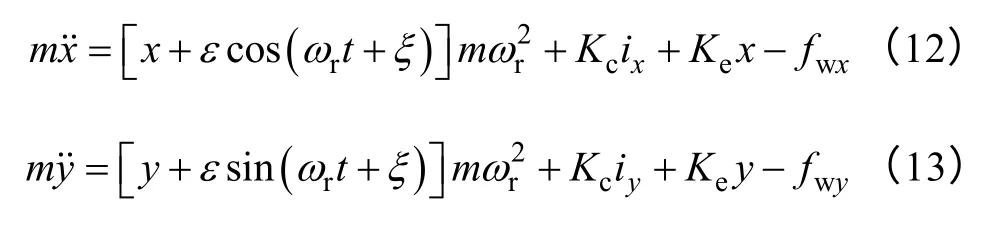
式中，fwx和fwy分別為轉子所受外力在x、y 方向上的分量，假設控制器中x 和y 方向的PID 調節器參數都是相同的，有

式中，kp，ki，kd分別為PID 調節器參數。

求解式（12）～式（15），可解得

式中

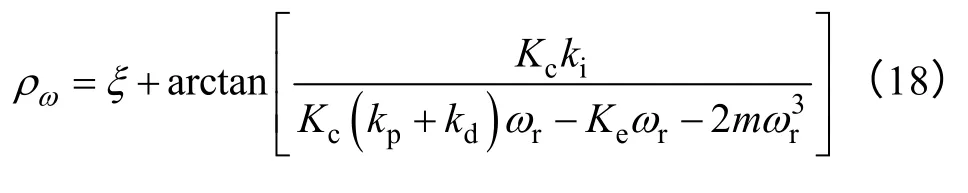
從式（16）可以看出，在轉子存在質量不平衡的情況下，無軸承異步電機徑向位移控制環僅采用PID 控制時，其轉子依然會產生周期性振動。所以，僅通過PID 控制不能消除無軸承異步電機轉子的周期性振動。

圖5 所示為考慮轉子質量不平衡時，仿真實驗中獲得的轉子x 方向位移曲線圖。而實際上，由于轉子外形存在圓度誤差，x 和y 方向上的位移曲線的幅值并不完全相同。

圖5 動不平衡引起的轉子振動位移波形Fig.5 Displacement waveform of rotor vibration caused by unbalance

從以上分析可以看出，無軸承異步電機懸浮控制中僅采用PID 反饋控制無法消除轉子質量偏心產生的周期性振動。為消除無軸承異步電機轉子的周期性振動，必須采用動不平衡補償方法。

4 無軸承異步電機動不平衡補償方法研究

本文采用的動不平衡補償方法基于位移最小控制原則。首先，為消除位移中的周期性分量，必須從檢測到的位移信號中提取出與轉子轉動頻率同頻的周期性信號；其次，對于該周期性同頻位移信號，將其變換到轉子同步坐標系下，在該同步坐標系下，同頻位移信號即轉變為直變量；然后，對該直變量進行PID 調制，即可產生在同步坐標系下的補償控制力分量，再將該補償控制力分量變換到αβ 靜止坐標系下，即可得到αβ 坐標系下動不平衡補償控制力分量，從而完成對動不平衡量的補償控制。以下將詳細闡述動不平衡補償方案。

4.1 同步信號獲取

為了獲取位移檢測信號中的同步分量，以往的做法[14,15]都是，將檢測的位移信號首先進行從靜止坐標系到同步旋轉坐標系的旋轉變換，然后采用一個低通濾波器來濾除信號中的高頻成分，再將信號經過旋轉反變換，即可得到檢測位移信號中的同步分量。然而這種方法只適用于固定帶寬轉子高速旋轉的情況下，為了使不平衡補償方法能夠在更寬的速度范圍內工作，本文采用傅里葉分析技術設計了一種同步信號獲取方法，具體流程如圖6 所示。

圖6 同步信號處理單元（SPU）Fig.6 Synchronous signal processing unit

基于圖6，可以得到同步位移信號如下：

式中 s(t)——原始位移信號；

sω(t)——同步位移信號；

ωr——電機轉子轉速；

T——旋轉周期；

a——同步正弦信號幅值；

b——同步余弦信號幅值。

如圖 6 所示，首先，檢測的位移信號分別與cos(ωrt)和sin(ωrt)相乘，然后進入積分器。在積分器中，除了與轉速同頻的同步信號外，其他倍頻信號及隨機信號將被濾除。與轉速同頻的同步信號經過積分器即變成與原始振動信號幅值成正比的直流信號。再將這個直流信號和與之對應的cos(ωrt)或sin(ωrt)相乘后即可得到傳感器檢測到的位移信號中的同頻成分。

為了實現可靠的同步信號獲取，本文所提出方法還需要滿足轉子轉速ωr穩定或緩慢變化的條件。而對于瞬態及轉子轉速快速變化情況下的同步信號穩定獲取還需要進一步研究。對于同步信號獲取模塊需要用到正余弦計算，本文所述的控制器采用FPGA 作為控制核心，正余弦值的獲取采用查表法，從而避免了計算的復雜性。同時由于FPGA 采用并行運算，相對于基于DSP 的懸浮控制系統，計算延時可大大縮小，因而完全能夠滿足電機高速運轉下控制系統的計算性能要求。

4.2 不平衡力補償方法

定義uv 坐標系為與轉子旋轉同步的旋轉坐標系，則轉子的同步位移信號和動不平衡離心力在uv同步旋轉坐標系下都是直變量。因此可以在uv 坐標系下對不平衡量進行補償控制。

不平衡力補償模塊如圖7 所示。檢測到的位移信號通過同步信號處理單元（SPU）獲得與轉速同頻的位移信號分量，然后將其進行Park 變換，從而轉換成同步坐標系下的直變分量su和sv，然后其與同步信號指令值比較，其偏差經過PID 調節器產生同步坐標系下的補償控制力，然后再將其進行Park-1變換，從而獲得在xy 坐標系下的不平衡補償控制力。

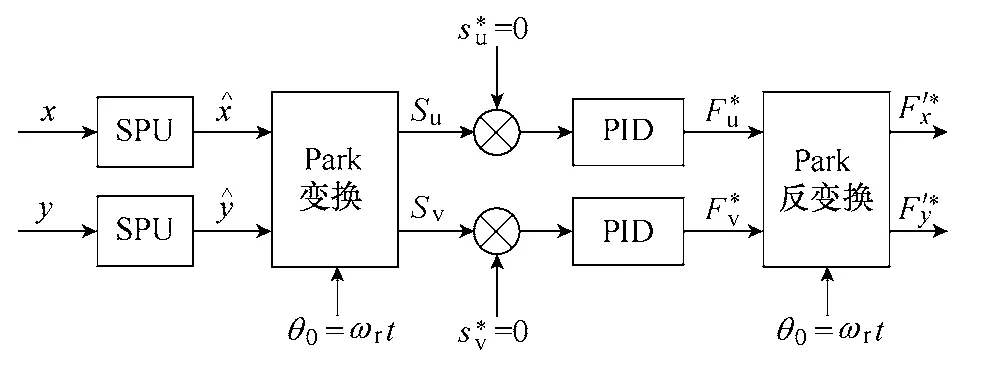
圖7 不平衡力補償模塊Fig.7 Unbalance force compensation module

4.3 基于不平衡力補償的無軸承異步電機控制系統

本文提出的采用動不平衡補償的無軸承異步電機控制框圖如圖8 所示。如圖所示，無軸承異步電機控制系統由轉矩控制子系統和懸浮控制子系統兩部分組成。轉矩控制子系統主要采用基于轉子磁場定向的矢量控制。對于懸浮控制子系統，電渦流傳感器檢測到的轉子徑向位置信息一方面傳遞給徑向位移控制環，和位移指令值的偏差經過不完全微分PID 控制器產生徑向懸浮力指令值；另一方面傳遞給不平衡力補償模塊獲得不平衡補償力指令值。懸浮力指令值和不平衡補償力指令值相加即可得到控制所需的懸浮力指令，由此可得所需的xy 方向控制電流懸浮控制繞組在αβ坐標系下的控制電流分量可由式（4）確定，再經過Clarke 反變換進行調制，從而產生懸浮繞組控制所需的三相參考電流值。

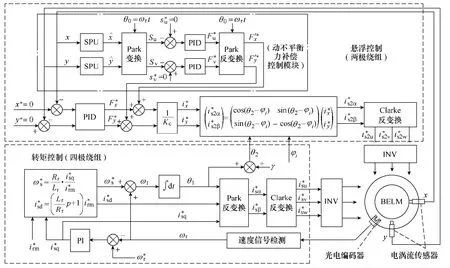
圖8 基于不平衡力補償的無軸承異步電機控制框圖Fig.8 Block diagram of a bearingless induction motor system based on unbalance compensation

5 實驗研究

本文研究的無軸承異步電機實驗樣機是在一臺型號為Y90L—4 的三相異步電機基礎上改造而成，實驗平臺如圖9 所示。如圖9 所示，樣機前端懸浮，后端采用調心軸承支承，后端蓋安裝光電編碼器以采集電機轉速信息。控制器采用Altera 公司生產的EP3C25E144 型號FPGA，兩套繞組的逆變器均采用智能功率模塊IPM，開關頻率為20kHz，控制器與上位PC 通過Ethernet 網絡通信。實驗樣機采用的徑向位移傳感器為清華大學精儀系桑拓應用技術研究所生產的電渦流傳感器，型號為ST—TC—03，量程為0.5mm，靈敏度為10mV/μm。

圖9 無軸承異步電機實驗平臺Fig.9 Platform of a bearingless induction motor

本文研究的無軸承異步電機實驗樣機的主要參數為：額定功率PN=1.5kW，額定轉速n=3 000r/min，轉子質量m=2.85kg，轉動慣量J=0.008 9kg·m2，電機氣隙長度 δ0=0.4mm，輔助軸承與轉軸的間隙為σ=200μm。兩套繞組的參數如下：轉矩繞組：定子電阻R1s=2.8Ω，轉子電阻Rr=1.75Ω，定子自感Ls=92.73mH，繞組互感 Lm=78.96mH，轉子自感 Lr=85.46mH，轉子漏感Llr=6.5mH，繞組匝數N1=42，極對數 p1=2；懸浮繞組：極對數 p2=1，繞組匝數N2=21。

圖10 所示為電機轉速n=1 300r/min 時加入動不平衡補償前的轉子徑向位移波形曲線圖及頻譜圖。從圖10a 和圖10c 中可以看出，轉子徑向位移呈周期性波動，x 方向和y 方向位移波動的峰峰值大約為40μm。從圖10b 和圖10d 中可以看出，在與轉速同頻（21.6Hz）的頻率成分處，轉子的x 向和y向的位移波動幅值分別為12.18μm 和9.593μm，為位移信號中主要成分。從圖中還可以看出，轉子的位移信號中除同頻分量外還包含高階倍頻分量，如圖10b 和圖10d 中二倍頻（43.2Hz）分量的幅值分別為1.413μm 和1.078μm。這與本文第三節轉子動力學的分析有些出入，這是因為，本文中對存在質量偏心的無軸承異步電機轉子運動學方程的推導是基于剛性體假設。而實際上，無軸承異步電機的轉軸亦是柔性體，且轉子外形由于制造工藝會有圓度誤差，從而造成外圓表面不嚴格規整。如此，由不平衡力及其他外力激發的高階諧波位移分量同樣會產生。而激發的高階諧波的幅值則由柔性轉軸自身特性決定。在本文提出的不平衡補償控制中，轉子高階諧波位移分量未被處理，而轉子高階諧波位移分量的抑制將是本文下一步研究的目標。

圖10 加入補償前轉子位移曲線及頻譜圖（1 300r/min）Fig.10 The waveform and frequency spectrum of rotor displacement without compensation at 1 300r/min

圖11 所示為電機轉速n=1 300r/min 時，加入動不平衡補償后的轉子徑向位移波形曲線圖及頻譜圖。從圖11a 和圖11c 中可以看出，轉子x 方向和y方向徑向位移的峰峰值大約為10μm，相比于加入動不平衡補償前，轉子徑向位移的峰峰值大大減小，轉子的懸浮精度得到很大提高。從圖11b 和圖11d中可以看出，在與轉速同頻（21.6Hz）的頻率成分處，轉子的x 向和y 向的位移波動幅值分別為0.785 5μm 和1.3μm。相對加入動不平衡補償前，轉子x 向和y 向徑向位移中與轉速同頻的周期性同步分量已得到很大抑制。而從圖11b 和圖11d 中亦可以看出，二倍頻分量（43.2Hz）處的位移分量幅值分別為2.107μm 和1.003μm。相對加入動不平衡補償前，該頻率成分處的位移波動未被抑制，這是因為對高頻位移分量的抑制研究未被納入本文的研究范圍，將是本文下一步工作的目標。

圖11 加入補償后轉子位移曲線及頻譜圖（1 300r/min）Fig.11 The waveform and frequency spectrum of rotor displacement with compensation at 1 300 r/min

為了進一步研究動不平衡補償控制策略的效果，本文開展了轉子轉速從1 000～3 000r/min 變化的動態懸浮實驗，位移峰峰值的實驗結果如圖 12所示。從圖12 可以看出，在未加入動不平衡補償時，轉子徑向位移的峰峰值隨轉速的增大而非線性增大，轉子位移波動依賴于轉子旋轉速度，可以確信該位移波動主要由轉子質量不平衡引起。同時，從圖中還可以看出，在加入補償控制前，轉子轉速在接近2 600r/min 時位移峰峰值出現一次較快的爬升，并在 2 600r/min 轉速位置上出現一個峰值，為107μm，說明無軸承異步電機的一階臨界轉速約為2 600r/min。然而，在采用動不平衡補償后，無軸承異步電機轉子振動得到了有效的抑制，整個位移峰峰值曲線接近于一條水平線，并且在一階臨界轉速處其位移波動與其他轉速的波動沒有太大區別。

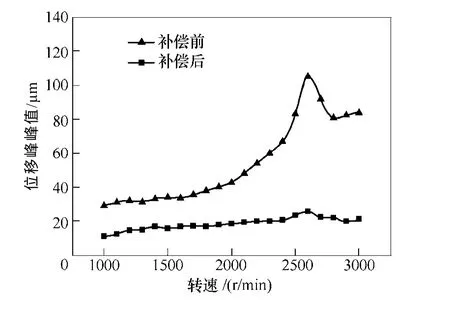
圖12 動不平衡補償前后的位移峰峰值曲線Fig.12 Rotor peak-peak displacement versus rotational speeds with and without compensation

6 結論

本文研究了無軸承異步電機中由于質量不平衡引起的轉子同步振動問題，并提出了一種基于前饋補償的動不平衡補償控制方案。通過在無軸承異步電機原有的懸浮控制系統上加上一個前饋控制，利用控制器產生一定的控制力來補償轉子不平衡離心力，強行約束轉子圍繞其幾何中心軸旋轉，從而達到轉子振動位移最小的目的。文中分析了無軸承異步電機不平衡振動產生的機理，并推導了徑向位移環僅采用PID 控制時的轉子運動學方程。在此基礎上，提出了一種基于前饋閉環補償的動不平衡補償方案。搭建了無軸承異步電機實驗平臺，開展了動不平衡補償前后的對比實驗。實驗結果表明，在轉子轉速為1 300r/min 下，加入不平衡補償前轉子徑向位移的峰峰值約為40μm，加入動不平衡補償控制后轉子徑向位移減小到約10μm，轉子振動減小了約75%，轉子懸浮精度大大提高，從而驗證了本文所提出動不平衡補償控制方案的有效性。此外，本文所研究的動不平衡補償控制方案亦可以推廣到其他類型的無軸承電機的懸浮控制中去。

附 錄

為了說明文中式（21）同步信號獲取過程，作以下補充。

在轉子質量存在不平衡時，轉子的運動方程可寫為

式中，Ak、Bk分別為k 倍頻振動信號的正弦分量和余弦分量的幅值；φk和φk為對應分量的相角；sn為隨機位移信號。

其中，與轉子轉速同頻分量為

則同步信號處理單元的處理過程可以表示為

從而有

如此，原始信號經過同步信號處理單元后，得到的即為與轉速同頻的振動信號。

[1]孫曉東,陳龍,楊澤斌,等.考慮偏心及繞組耦合的無軸承永磁同步電機建模[J].電工技術學報,2013,28(3):63-70.Sun Xiaodong,Chen long,Yang Zebin,et al.Modeling of a bearingless permanent magnet synchronous motor considering rotor eccentricity and coupling relationship of windings[J].Transactions of China Electrotechnical Society,2013,28(3):63-70.

[2]孫曉東,朱熀秋.基于神經網絡逆系統理論無軸承異步電動機解耦控制[J].電工技術學報,2010,25(1):43-49.Sun Xiaodong,Zhu Huangqiu.Decoupling control of bearingless induction motors based on neural network inverse system method[J].Transactions of China Electrotechnical Society,2010,25(1):43-49.

[3]鄧智泉,嚴仰光.無軸承交流電動機的基本理論和研究現狀[J].電工技術學報,2000,15(2):29-35.Deng Zhiquan,Yan Yangguang.The main theory and status quo of AC bearingless motors[J].Transactions of China Electrotechnical Society,2000,15(2):29-35.

[4]王鳳翔,鄭柒拾,王寶國.不同轉子結構無軸承電動機的磁懸浮力分析與計算[J].電工技術學報,2000,15(5):6-9.Wang Fengxiang,Zheng Qishi,Wang Baoguo.Analysis and calculation of magnetic levitation forces for bearingless motors with different rotor structure[J].Transactions of China Electrotechnical Society,2000,15(5):6-9.

[5]Shi J,Zmood R,Qin L.Synchronous disturbance attenuation in magnetic bearing systems using adaptive compensation signals[J].Control Engineering Practice,2004,12(3):283-290.

[6]Bi C,Wu D Z,Jiang Q,et al.Optimize control current in magnetic bearings using automatic learning control[C].Proceedings of IEEE International Conference on Mechatronics,Istanbul,Turkey,2004:305-310.

[7]Kuseyri I S.Robust control and unbalance compensation of rotor/active magnetic bearing systems[J].Journal of Vibration and Control,2012,18(6):817-832.

[8]Li L,Shinshi T,Iijima C,et al.Compensation of rotor imbalance for precision rotation of a planar magnetic bearing rotor[J].Precision Engineering,2003,27(2):140-150.

[9]Lum K Y,Coppola V T,Bernstein D S.Adaptive autocentering control for an active magnetic bearing supporting a rotor with unknown mass imbalance[J].IEEE Transactions on Control System Technology,1996,4(5):587-597.

[10]Tang L,Chen Y Q.Model development and adaptive imbalance vibration control of magnetic suspended system[J].Acta Astronautica,2009,65(9-10):1506-1514.

[11]Hector G C,Pablo S M.Unbalance compensation for active magnetic bearings using ILC[C].Proceedings of the IEEE International Conference on Control Applications,Mexico,2001:58-63.

[12]Herzog R,Buhler P,Gahler C,et al.Unbalance compensation using generalized notch filters in the multivariable feedback of magnetic bearings[J].IEEE Transactions on Control System Technology,1996,4(5):580-586.

[13]Setiewan J D,Mukherjee R,Maslen E H.Synchronous sensor runout and unbalance compensation in active magnetic bearings using bias current excitation[J].Journal of Dynamic Systems,Measurement and Control,2002,124(1):14-24.

[14]張濤,倪偉,葉小婷.基于電流最小的無軸承永磁電機轉子質量不平衡補償控制[C].Proceedings of the 27th Chinese Control Conference,Kunming,China,2008:164-168.

[15]張濤,朱熀秋.無軸承永磁同步電機轉子質量不平衡補償控制[J].中國電機工程學報,2007,27(15):33-37.Zhang Tao,Zhu Huangqiu.Rotor’s mass unbalance compensation control in bearingless permanent magnettype synchronous motors[J].Proceedings of the CSEE,2007,27(15):33-37.

[16]張倩影,鄧智泉,楊艷.無軸承開關磁阻電機轉子質量偏心補償控制[J].中國電機工程學報,2011,31(21):128-134.Zhang Qianying,Deng Zhiquan,Yang Yan.Compensation control of rotor mass eccentric in bearingless switched reluctance motors[J].Proceedings of the CSEE,2011,31(21):128-134.

[17]卜文紹.無軸承電機通用磁懸浮模型及解耦控制系統研究[D].武漢:華中科技大學,2007.

[18]Chiba A,Fukao T,Ichikawa O,et al.Magnetic bearings and bearingless drives[M].Boston:Newnes Elsevier,2005.

[19]Nornura S,Chiba A,Nakamura F,et al.A radial position control of induction type bearingless motor considering phase delay caused by the rotor squirrel cage[C].Power Conversion Conference,Yokohama,Japan,1993:438-443.

[20]Bu W S,Xiao J Y,Yuan L,et al.Induction compensation control of bearingless induction motor[C].Proceedings of the IEEE International Conference on Mechatronics and Automation,Beijing,China,2011:944-949.