彈靶尺寸對陶瓷／金屬復合裝甲防護性能的影響＊

遲潤強，Ahmad Serjouei ，范 峰，Idapalapati Sridhar

（1.哈爾濱工業大學土木工程學院，黑龍江 哈爾濱150001；2.School of Mechanical ＆ Aerospace Engineering，Nanyang Technological University，Singapore 639798）

陶瓷材料因具有高抗壓強度、高硬度及低密度等突出優點而越來越廣泛地被應用于裝甲防彈領域。將陶瓷材料與塑性較好的金屬材料復合在一起，可以更好地發揮2種材料各自的優點，提高防彈性能。獲取陶瓷／金屬復合裝甲彈道極限速度是一個很重要的工程問題，數值模擬是解決此問題的有效手段。相對于實驗方法，經過標定的數值模型不僅能夠提供較為準確的彈道極限速度結果，還可以直觀地分析侵徹過程，且耗費不大。目前，在對陶瓷／金屬復合裝甲撞擊的數值模擬研究中，最普遍應用的是Lagrange模型，但其不能很好地處理單元大變形以及表征脆性材料的破碎問題。

為了解決上述問題，部分研究采用了SPH模型［1］，但SPH方法存在不穩定性，SPH粒子可能出現受拉失穩的問題［2］。因此，本文中采用將上述2種方法結合在一起的SPH－Lagrange模型，可以消除單一數值方法的局限性，提供更準確的模擬結果。利用Autodyn軟件，建立經過實驗標定的SPH－Lagrange數值模型進行數值計算，分析陶瓷／金屬復合裝甲彈道極限速度與彈靶尺寸的具體關系，并建立裝甲彈道極限速度的經驗公式。

1 數值模擬

選取文獻［3］中的3個20mm脫殼穿甲彈（簡稱APDS子彈）撞擊陶瓷／金屬復合裝甲實驗作為驗證數值模擬有效性的依據。復合裝甲由99.5%氧化鋁陶瓷前板及5083－H111鋁合金后板組成，各次實驗的前、后板厚度見表1，表中T1、T2分別表示前、后板的厚度，l為子彈剩余長度，v為子彈剩余速度。

表1 APDS子彈侵徹氧化鋁陶瓷／鋁合金復合裝甲的實驗與數值模擬結果［3］Table 1 Experimental and simulation results for APDS impacting bi－layer alumina／aluminum armor［3］

在所有實驗中，APDS子彈以1 240m／s的速度垂直撞擊復合裝甲。20mm APDS子彈是一種次口徑大威力子彈，由鎢合金彈芯及輕質材料制作的風帽組成，直徑12mm，長度61.5mm，質量72g［4］。在實驗中，V.S.Gálvez［3］測量了APDS子彈穿透裝甲之后的剩余長度和剩余速度，見表1。

利用Autodyn軟件，采用二維軸對稱模型，對上述實驗工況進行數值模擬，有限元模型見圖1。鑒于鎢合金彈芯占20mm APDS子彈總質量的99%以上，僅建立了鎢合金彈芯的有限元模型來代替APDS子彈，忽略了風帽對撞擊效果的影響。APDS子彈與陶瓷前板為無網格的SPH模型，鋁合金后板為有網格的Lagrange模型，前板的SPH粒子與后板有限元網格的邊及節點在交界面上重合并利用Autodyn的“Join”功能固連在一起。裝甲前、后板徑向邊界處均設置軸向與徑向固定約束。

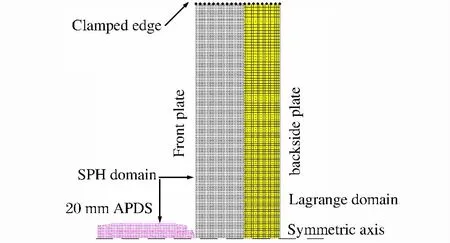
圖1 二維軸對稱數值模型Fig.1 Two－dimensional axisymmetric numerical model

采用SPH方法對子彈和陶瓷前板建模的主要原因［5］如下：如果APDS子彈與陶瓷前板是Lagrange模型，當彈靶接觸區域內的單元在撞擊過程中變形增大到一定程度，Autodyn軟件通常會采用刪除這些單元的方式（即侵蝕算法）來保證計算能夠持續進行，此時陶瓷材料前部的壓力會因單元消失而在短時間內突然消失，從而直接影響相鄰位置陶瓷單元內的壓力狀態，而陶瓷材料在力作用下的響應受到施加在自身上的壓力的影響很大，因此這會造成陶瓷材料強度降低；在SPH模型中，SPH粒子并不會因為材料大變形而被刪除，陶瓷前部的壓力會一直保持并連續變化，陶瓷材料的強度不會瞬間降低，能夠保證計算結果的準確性。另外，陶瓷為脆性材料，在撞擊下必然發生破碎；因為沒有網格的限制，SPH模型能夠更好的表現陶瓷破碎之后的運動。

鑒于5083－H111鋁合金的材料參數較難從文獻中獲取，在本文中采用5083－H116鋁合金的參數代替。5083－H116鋁合金與鎢合金材料均采用Johnson－cook本構模型［6］與失效模型［7］描述，具體參數參見文獻［8－9］。其中，5083－H116鋁合金JC失效模型中的參數d4未采用文獻［8］供的數值，這是因為文獻中采用的是一種修正的JC失效模型，其表達式與Autodyn材料庫中的原始JC失效模型不同。本文中根據該文獻所提供的實驗數據點，基于原始JC失效模型表達式，采用曲線擬合方法確定該參數值。氧化鋁陶瓷采用JH－2材料模型［10］，該模型被廣泛用于描述脆性材料在高壓、高應變率和大變形條件下的力學響應，包括3個部分：強度模型、損傷模型和狀態方程，99.5%氧化鋁材料所采用的JH－2模型參數參見文獻［11－12］。

圖2給出了APDS子彈侵徹裝甲的數值模擬過程。

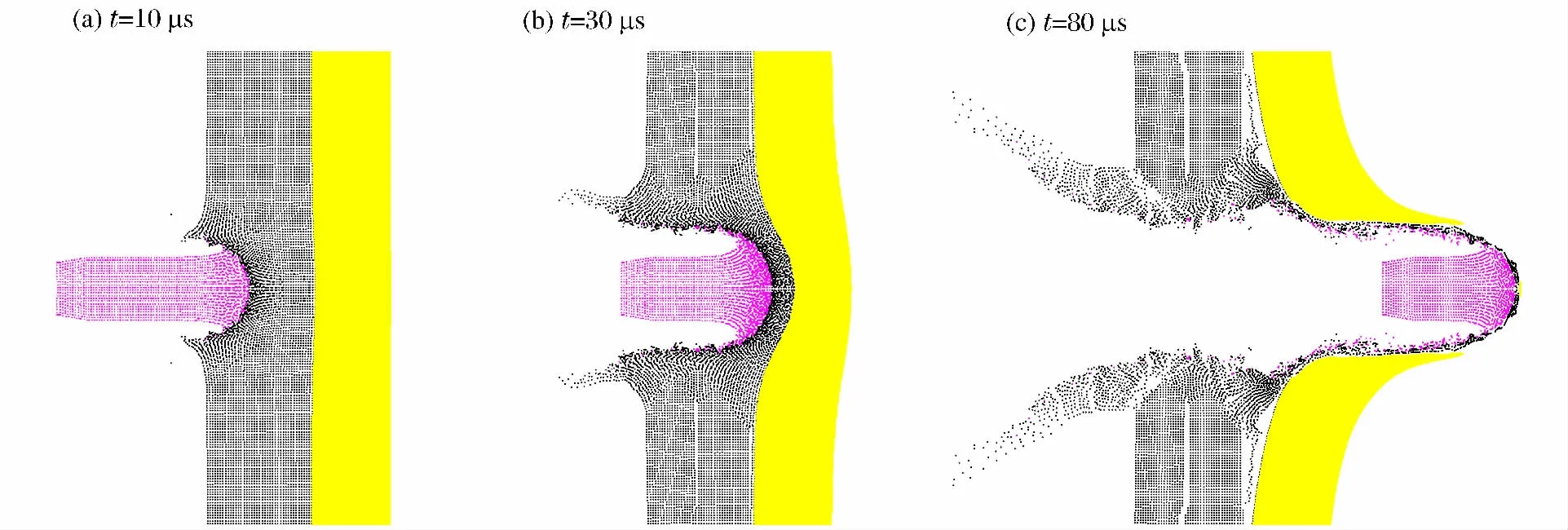
圖2 APDS子彈侵徹氧化鋁陶瓷／鋁合金復合裝甲的過程Fig.2 The process of APDS impacting alumina／aluminum armor

由圖2可見，前板中破碎的陶瓷材料和子彈前部被侵蝕掉的鎢合金材料可以自由運動，模擬結果更接近實際的物理現象，證明SPH方法模擬大變形和破碎行為的有效性。此外，數值模擬還給出了AP－DS子彈在穿透裝甲后的剩余速度與剩余長度，如表1所示。比較可見，數值模擬結果與實驗結果符合較好，說明本文中的有限元模型能夠有效模擬包含上述3種材料的子彈侵徹陶瓷／金屬復合裝甲問題。

2 彈靶尺寸對裝甲彈道極限速度的影響

利用上述有限元建模方法與材料參數，改變彈靶尺寸，進行一系列數值計算。考慮到APDS子彈彈芯的幾何形狀比較復雜，采用具有代表性的圓柱體子彈，便于對其形狀進行幾何描述。彈靶尺寸參數包括：子彈直徑d與長度L、圓形前板厚度T1與直徑D1、圓形后板厚度T2與直徑D2。通過改變數值模擬中的撞擊速度，采用逐漸逼近的方法，獲得了在不同彈靶尺寸組合下裝甲的彈道極限速度vL。

對子彈穿甲過程進行量綱分析，并通過數值模擬發現：當彈靶材料不變而尺寸變化時所有材料參數對裝甲彈道極限速度無影響。因此，裝甲彈道極限速度vL可表示為：

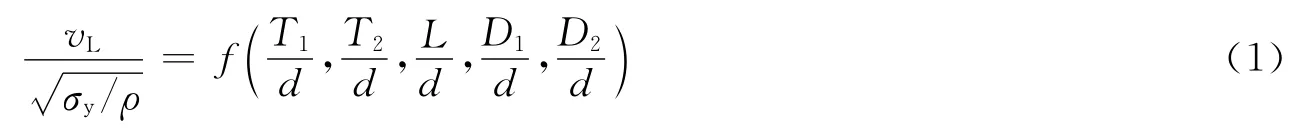
式中：σy與ρ分別為子彈材料的屈服強度與密度。

進一步，將vL的表達式寫為：

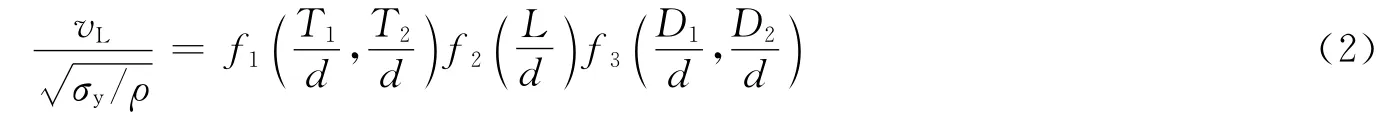
式中：f1、f2和f3為3個子函數，分別表述各尺寸參數與裝甲彈道極限速度的關系。

基于數值模擬結果，分別分析T1／d、T2／d、L／d、D1／d與D2／d對vL的影響規律并確定上述各子函數的形式。當考慮某一個參數的影響時，其他參數均保持不變，子彈直徑d均為12mm。

2.1 T1／d與T2／d對裝甲彈道極限速度的影響

函數f1同時考慮了T1／d與T2／d對彈道極限速度的影響。對此共進行了4組數值模擬，采用控制變量法 ，分別考慮T1／d與T2／d對復合裝甲彈道極限速度的影響，如圖3～4所示，以及對單層靶板彈道極限速度的影響，如圖5～6所示。

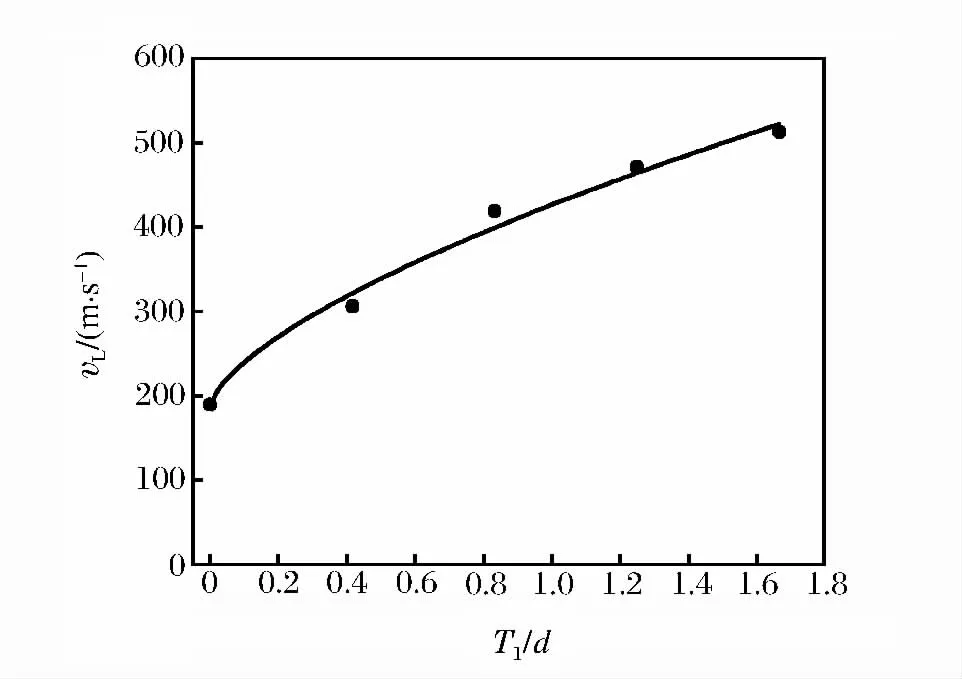
圖3 復合裝甲彈道極限速度隨T1／d比值變化關系Fig.3 Variation of ballistic limit velocity in composite armor with the ratio of T1／d

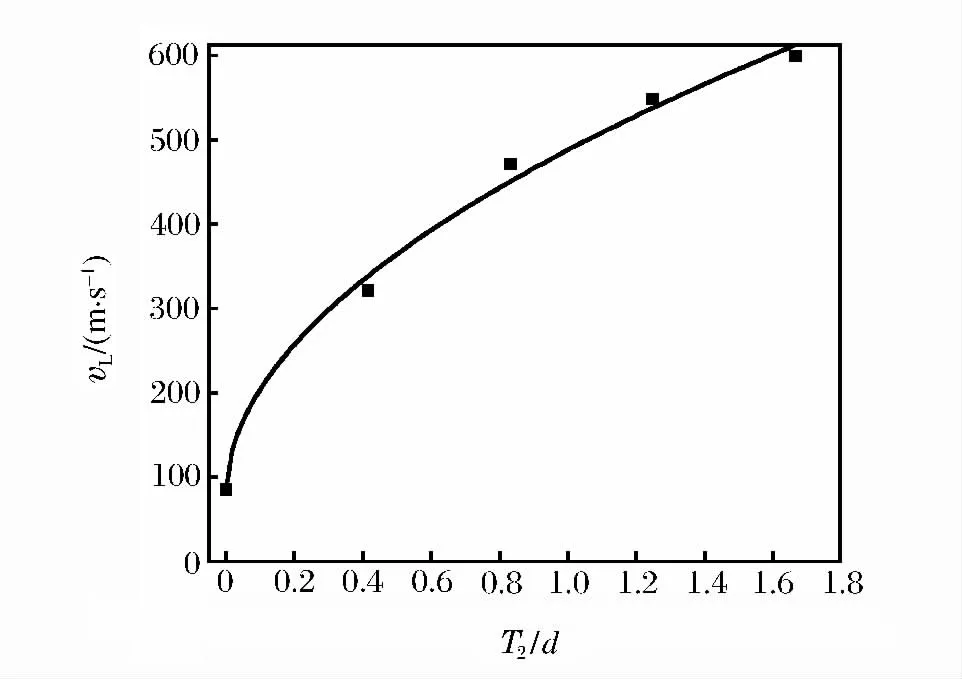
圖4 復合裝甲彈道極限速度隨T2／d比值變化關系Fig.4 Variation of ballistic limit velocity in composite armor with the ratio of T2／d

圖3～6中對應的靶板的幾何參數為L／d＝3，D1／d＝D2／d＝16.67。圖3中設T2／d＝0.83，圖4中設T1／d＝1.25；圖5～6中，由于只考慮單層靶板，因此對應的條件T1／d＝0和T2／d＝0。由圖中可知，vL隨T1／d與T2／d的增加而增加，且可認為其與二者近似呈冪函數關系。另外，相同厚度的單層鋁合金板比單層氧化鋁陶瓷板具有更高的彈道極限速度。

綜合以上分析，提出子函數f1的表達式如下：

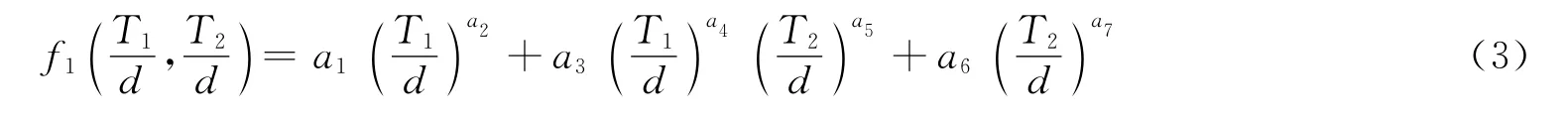
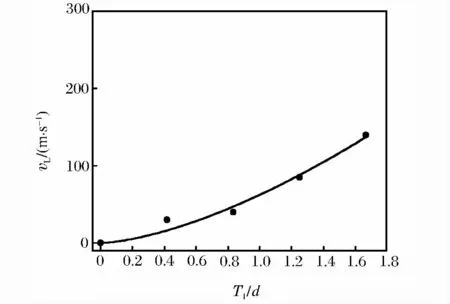
圖5 單層裝甲彈道極限速度隨T1／d比值變化關系Fig.5 Variation of ballistic limit velocity in single plate with the ratio of T1／d

圖6 單層裝甲彈道極限速度隨T2／d比值變化關系Fig.6 Variation of ballistic limit velocity in single plate with the ratio of T2／d

式中：a1～a7為待定系數。

2.2 L／d對裝甲彈道極限速度的影響

對5個具有不同L／d值的子彈撞擊裝甲的工況進行了數值模擬，圖7給出了彈道極限速度vL與L／d的關系，圖7中對應的復合靶板的幾何參數為T1／d＝T2／d＝0.83，D1／d＝D2／d＝16.67。由圖中可知，vL隨L／d的增加而降低，將其用冪函數表示如下：

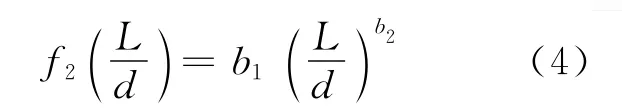
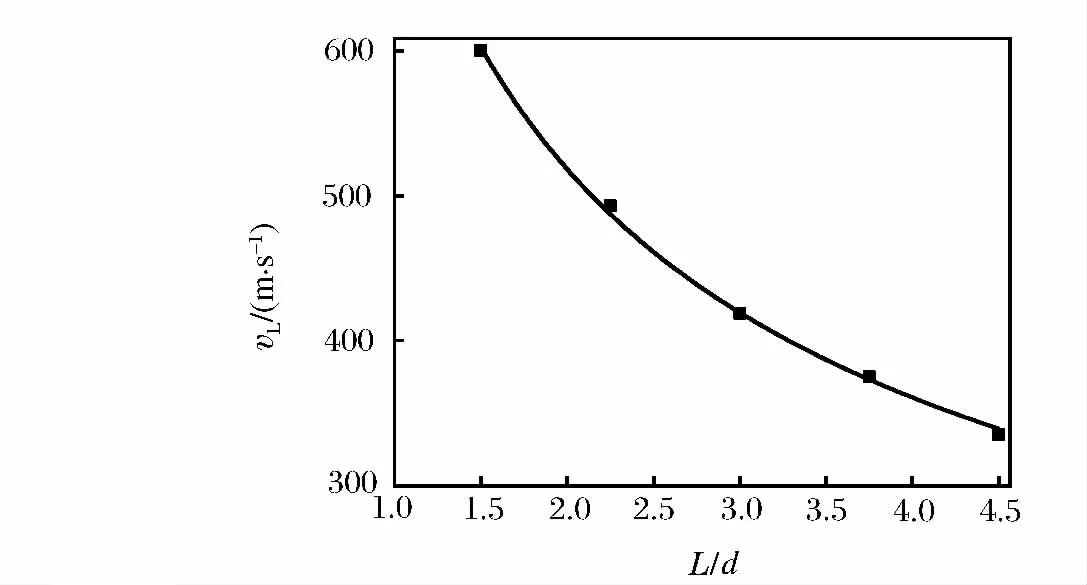
圖7 復合裝甲彈道極限速度隨L／d比值變化關系Fig.7 Variation of ballistic limit velocity in composite armor with the ratio of L／d

式中：b1、b2為待定系數。

2.3 D1／d與D2／d對裝甲彈道極限速度的影響

由于陶瓷前板與金屬后板材料特性相差很大，二者的平面尺寸對裝甲彈道極限速度的影響規律必然有較大差異。考慮到裝甲前、后板的平面尺寸在實際情形中不可能小于子彈直徑，在模擬中，D1／d與D2／d均大于1。

陶瓷是一種脆性材料，受力所產生的塑性變形很小，在子彈撞擊下，陶瓷前板的破碎主要發生在撞擊點附近的錐形區域內，該區域以外的陶瓷材料基本不參與子彈對裝甲后板的侵徹過程。因此，可認為當陶瓷板平面尺寸在小于陶瓷錐尺寸的范圍內變化時才對裝甲彈道極限速度產生影響。

為了驗證此觀點的正確性，對不同D1／d值工況下的復合裝甲進行了撞擊模擬，圖8給出了裝甲彈道極限速度與D1／d的關系。圖8中對應的復合靶板的幾何參數為L／d＝3，T1／d＝T2／d＝0.83，D2／d＝16.67。

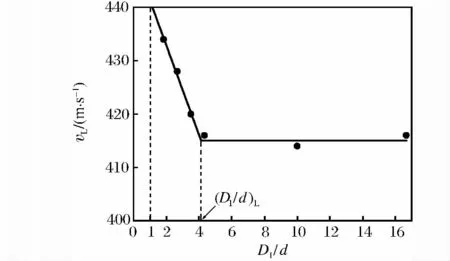
圖8 復合裝甲彈道極限速度隨D1／d比值變化關系Fig.8 Variation of ballistic limit velocity in composite armor with the ratio of D1／d

由圖8可見，彈道極限速度vL隨D1／d的增加并非單調變化。存在一個臨界值當時，vL隨D1／d的增加而線性減小，當時，vL保持不變。對圖8中的計算值進行分段曲線擬合，獲得了D1／d在有效范圍內所對應的vL值，確定2條曲線分界點當 D1／d＝1時，對應vL的最大值；當時，對應vL的最小值。若以彈道極限速度的最小值為標準，2個極值之差與其相比不超過6%，這說明D1／d的變化對裝甲彈道極限速度的影響不明顯。

圖9給出了復合裝甲中陶瓷前板在子彈侵徹過程中形成的錐形陶瓷破碎區形態。根據計算得到陶瓷前板臨界平面尺寸也被標注在圖中，比較發現幾乎與陶瓷破碎錐最大直徑相同。綜上說明：對于僅陶瓷前板平面尺寸不同而其他彈靶參數均相同的撞擊，必然存在一個臨界前板平面尺寸，該尺寸即為陶瓷破碎錐直徑最大值；僅當陶瓷前板平面尺寸小于該臨界值時，其變化才對裝甲彈道極限速度產生影響。

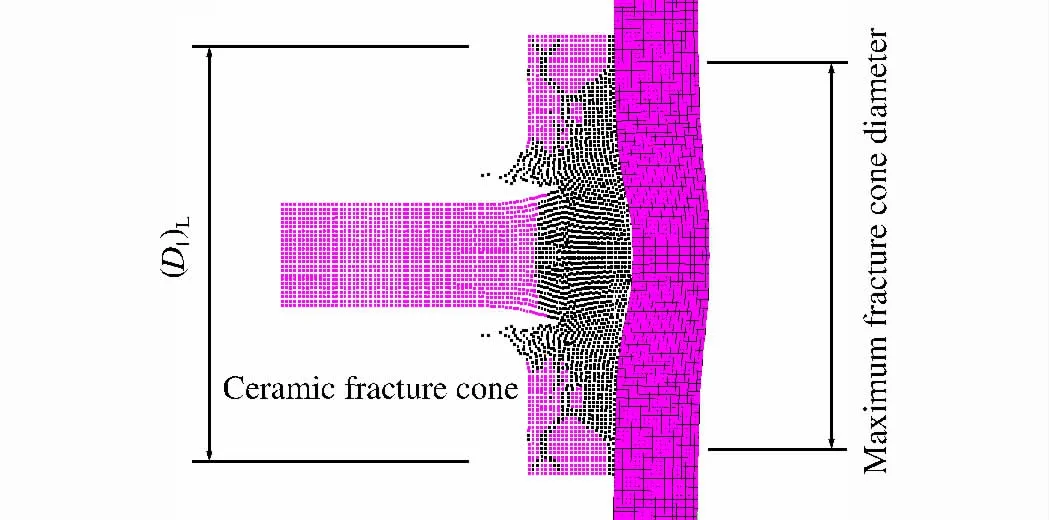
圖9 彈體撞擊過程中陶瓷破碎錐的最大直徑Fig.9 Ceramic maximum fracture cone diameter in process of impacting

為了解釋vL隨D1／d（1＜D1／d＜ （D1／d）L）增加而減小的現象，對2個不同組合的裝甲開展相同速度撞擊的數值模擬，如圖10所示，除陶瓷前板平面尺寸外，其余彈靶參數均相同。

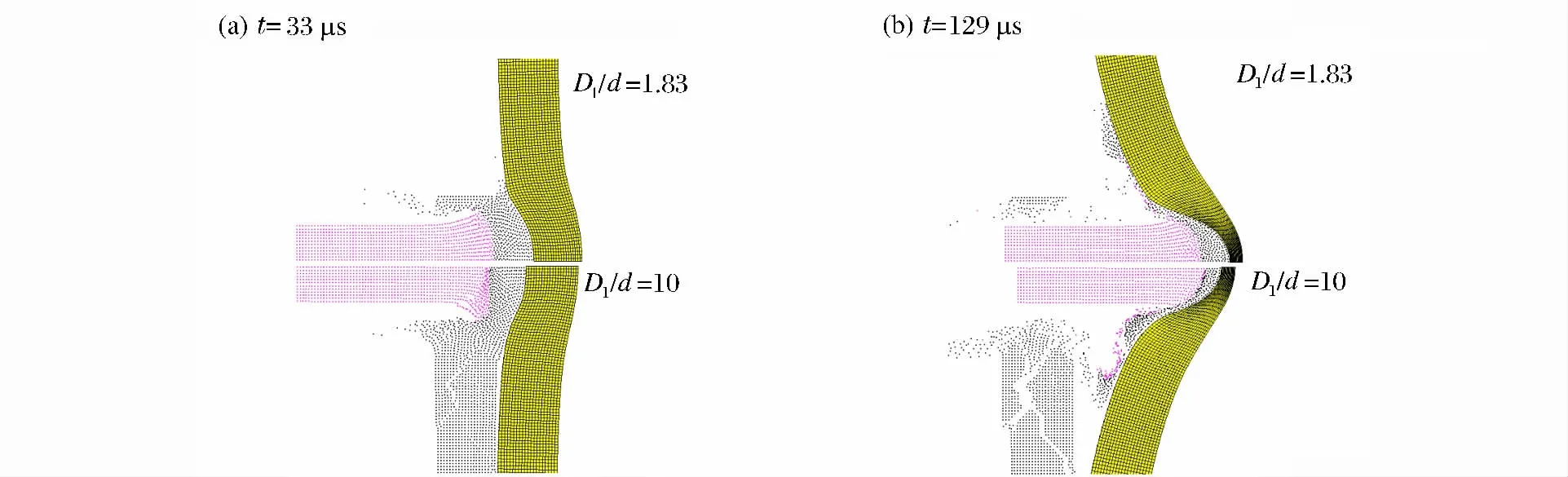
圖10 具有不同D1／d值的裝甲被撞擊時的形態比較Fig.10 Impacting mode comparison for two armors with different D1／d

裝甲Ⅰ和裝甲Ⅱ的D1／d值分別取1.83和10，二者位于的兩側，且差別較大，這樣可以更清晰地看出其對撞擊過程影響的區別。圖10給出了不同組合的裝甲在子彈撞擊過程中2個時刻的形態，圖形上半部分對應裝甲Ⅰ，下半部分對應裝甲Ⅱ。在33μs時刻，2種裝甲中鋁合金后板的變形明顯不同，相比于裝甲Ⅱ，裝甲Ⅰ中后板的變形更集中于中間部分，這使其能夠更有效地限制破碎的陶瓷材料沿徑向擴散，直到撞擊過程后期129μs時刻，子彈與后板之間仍保存有更多的陶瓷材料，從而增大子彈與陶瓷材料在后板上的作用面積，使其后板更難被穿透。因此，裝甲Ⅰ的彈道極限速度相對于裝甲Ⅱ的更高。

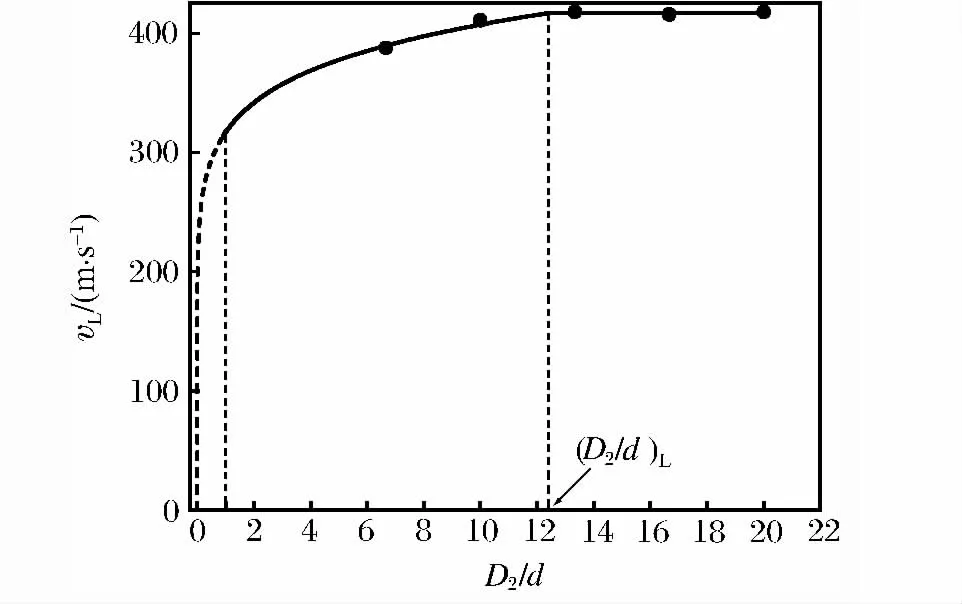
圖11 復合裝甲彈道極限速度隨D2／d比值變化關系Fig.11 Variation of ballistic limit velocity in composite armor with the ratio of D2／d

復合裝甲后板為鋁合金材料，具有較好的塑性，可以預測，在沖擊下其塑性變形應該存在于一個較大的平面范圍內。對具有不同D2／d值的復合裝甲進行撞擊的數值模擬，彈道極限速度vL與D2／d的關系如圖11所示。圖11中對應的復合靶板的幾何參數為L／d＝3，T1／d＝T2／d＝0.83。復合裝甲的D1／d值與D2／d保持相同，并且大于 （D1／d）L，以消除前者對彈道極限速度的影響。

對圖11中的數據進行分段曲線擬合，獲得2條曲線，二者分界點設為當時，vL隨D2／d的增加而增加；當時，vL為定值。若以圖11中彈道極限速度最大值為標準，2個極值之差與其之比為24.5%。此外，明顯大于這些都說明D2／d對于彈道極限速度的影響大于D1／d的影響。

根據圖8和圖11中所示裝甲彈道極限速度與D1／d及D2／d的關系，并考慮D1／d不能大于D2／d，且在范圍內，提出子函數f3的形式如下：

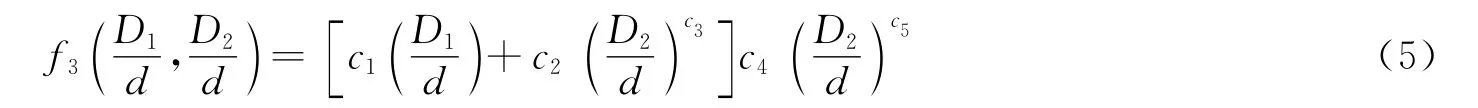
式中：c1～c5為待定系數。從量綱的角度看，分界點應隨L／d、T1／d和T2／d的變化而變化，但該問題非本文研究重點，暫未開展工作。

2.4 裝甲彈道極限速度的經驗方程

將前文中已獲得的3個子函數表達式帶入式（2），即可得到復合裝甲彈道極限速度表達式。基于該式，利用數值模擬結果，采用最小二乘法進行回歸分析，便可獲得各待定系數的值。考慮到通常情況下裝甲前后板的平面尺寸往往比子彈直徑大的多，在模擬中忽略了子彈直徑對彈道極限速度的影響，取D1／d＝D2／d＝20。最后獲得氧化鋁陶瓷（99.5%）／鋁合金（Al 5083－H116）復合裝甲在鎢合金子彈撞擊下的彈道極限速度與彈靶幾何參數L／d、T1／d和T2／d之間關系的經驗公式如下：

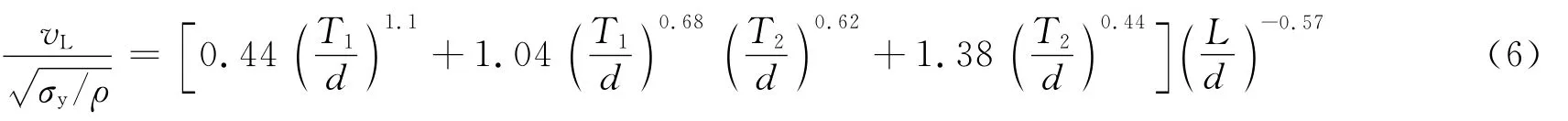
盡管式（6）僅適用于本文中所涉及的彈靶材料，但可預見的是，其方程形式以及各幾何參數對陶瓷／金屬復合裝甲的影響規律可以推廣到更多材料。

3 結 論

利用數值模擬手段對氧化鋁陶瓷／鋁合金復合裝甲在鎢合金子彈撞擊下的彈道極限速度與彈靶尺寸之間的關系進行了分析。研究發現：裝甲彈道極限速度隨T1／d和T2／d的增加而增大，隨L／d的增加而減小；D1／d與D2／d只在一定范圍內影響裝甲彈道極限速度，當二者超過其臨界值后，對彈道極限速度無影響；在影響范圍內，裝甲彈道極限速度隨D1／d的增加而線性減小，隨D2／d的增加而增大。此外還分析了D1／d影響裝甲彈道極限速度的機理。建立一個裝甲彈道極限速度的經驗公式，其形式可作為其他陶瓷／金屬復合裝甲彈道極限速度的研究提供參考。

［1］張偉，胡德安，韓旭，等.陶瓷／金屬復合裝甲沖擊響應的三維SPH 法分析［J］.爆炸與沖擊，2011，31（4）：373－379.Zhang Wei，Hu De－an，Han Xu，et al.Three－dimensional SPH analysis of impact responses of ceramic／metal composite armors［J］.Explosion and Shock Waves，2011，31（4）：373－379.

［2］Swegle J W，Hicks D L，Attaway S W.Smoothed particle hydrodynamics stability analysis［J］.Journal of Computational Physics，1995，116（1）：123－134.

［3］Gálvez V S，Paradela L S.Analysis of failure of add－on armour for vehicle protection against ballistic impact［J］.Engineering Failure Analysis，2009，16（6）：1837－1845.

［4］Abrate S.Impact engineering of composite structures［M］.New York：Springer，2011.

［5］Johnson G R，Stryk R A，Beissel S R，et al.An algorithm to automatically convert distorted finite elements into meshless particles during dynamic deformation［J］.International Journal of Impact Engineering，2002，27（10）：997－1013.

［6］Johnson G R，Cook W H.A constitutive model and data for metals subjected to large strains，high strain rates and high temperatures［C］∥Proceedings of the Seventh International Symposium on Ballistics.Netherlands，1983：541－547.

［7］Johnson G R，Cook W H.Fracture characteristics of three metals subjected to various strains，strain rates，temperatures and pressures［J］.Engineering Fracture Mechnics，1985，21（1）：31－48.

［8］Clausen A H，Borvik T，Hopperstad O S，et al.Flow and fracture characteristics of aluminium alloy AA5083－H116as function of strain rate，temperature and triaxiality［J］.Materials Science and Engineering：A，2004，364（1／2）：260－272.

［9］Lee J K.Analysis of multi－layered materials under high velocity impact using CTH［D］.Ohio：Air Force Institute of Technology，2008.

［10］Johnson G R，Holmquist T J.An improved computational constitutive model for brittle materials［J］.AIP Conference Proceedings，1994，309（1）：981－984.

［11］Anderson C E，Johnson G R，Holmquist T J.Ballistic experiments and computations of confined 99.5%AL2O3 ceramic tiles［C］∥Proceeding of Fifteenth International Symposium on Ballistics.Jerusalem，Israel，1995.

［12］Lundberg P，Westerling L，Lundberg B.Influence of scale on the penetration of tungsten rods into steel－backed alumina targets［J］.International Journal of Impact Engineering，1996，18（4）：403－416.