鋼框架結構正弦掃頻振動臺試驗的虛擬實現*

劉紅彪，張 強，劉現鵬，張寶華，田雙珠

0 引言

虛擬設計技術是隨著計算機技術的發展而產生的新興技術，被廣泛應用于機械制造、航空航天等領域的產品前期規劃、設計、試驗等各個階段。由于采用傳統工業產品設計方法設計的產品，其結構、功能、操作性能等方面的缺陷往往會在產品開發后期或產品最終試車過程中被發現，進而導致產品需進一步改進設計，導致產品的開發效率低，開發費用增加。采用計算機仿真技術和虛擬實現技術的虛擬設計方法可以大大提高產品的設計效率和質量，提高了產品的市場競爭力(楊志勇，唐勝利，2006)。

正弦掃頻試驗和隨機振動試驗是檢驗產品可靠性，解決各種機械結構振動問題的重要手段，廣泛應用于航空航天、汽車以及包裝運輸等領域，且為結構環境振動試驗的核心 (田光明，2005;楊志東等，2008)。在航天產品的研制過程中，正弦掃頻試驗尤為重要，它是結構模態參數識別的重要手段，產品在正弦掃頻下的動力響應結果是重點關注的方面，正弦掃頻試驗下的結構動力響應結果是反應產品合格與否的重要指標。試驗設計的合理性、荷載量級及加載順序是關系結構正弦掃頻振動臺試驗成敗的關鍵。根據虛擬設計的概念，采用虛擬設計方法對結構正弦掃頻振動臺試驗進行前期的規劃、設計、優化，可有效提高試驗成功的概率。

本文提出正弦掃頻振動臺的虛擬設計方法，并精確推導出正弦掃頻函數的表示方法，并以此分析正反向正弦掃頻試驗過程中結構動力反應的差異問題，同時給出環境振動試驗中的夾具選擇原則，以此建立正弦掃頻振動臺試驗的虛擬設計方法。該研究對指導土木、機械及航空領域產品的正弦掃頻試驗，合理評估產品在掃頻過程中的動力響應均具有參考價值。

1 正弦掃頻函數的數學描述

某些抗震試驗中 (劉紅彪，2012;劉紅彪，郭迅，2012;周寶峰等，2013)，采用 y(t)=Asin［2πtf(t)］，f(t)=2t/4，t∈［0，24］作為正弦掃頻函數，似乎可以生成1～64 Hz的正弦掃頻函數，其實不然，該函數忽略了函數的頻率值是由tf(t)共同決定的，實際生成的掃頻信號的頻率范圍為1～330 Hz。為了獲取正弦掃頻函數在時域上的精確描述，根據相關理論，進行了如下推導。

一般正弦掃頻函數可表述為

其中:φ0為初相位;設正弦函數隨時間變化的頻率為f(t)，則f(t)=φ'(t)/2π。根據頻率變化的規律，頻率變化可分為線性變化和對數變化。若正弦掃頻函數的頻率按照線性變化，則頻率變化率可表述為

根據積分可得

若t=0時的起始頻率為f0，t=t1時刻的截止頻率為f1，則c1=f0，k=(f1－f0)/(t1－t0);考慮到 c2和φ0可以組成新的初相位，則φ(t)可表示為

由此，正弦掃頻函數y(t)可描述為但線性變化時，頻率變化緩慢，達到預期頻率花費時間長，一般不采用，試驗中常用對數掃頻。對數掃頻中的頻率值可表示為

對 (2)經積分可求得

考慮到c和φ0可以組成新的初相位，則φ(t)可表示為

將 (8)式代入 (1)式，則正弦掃頻函數y(t)可描述為

一般在正弦掃頻試驗時，采用的掃描速率單位為oct/min，且不考慮初相位，故式 (9)可改寫為

其中，f0為起始頻率，r為掃頻速率 (oct/min)。

2 鋼框架結構正弦掃振動臺試驗的仿真分析

機械領域的結構環境振動試驗屬于高頻范疇，由于被測試件的結構固有頻率較高，電磁振動臺的臺面作為獨立結構件與試驗件耦合，其動力特性對試驗件的動力響應有一定影響。但一般民用建筑結構的固有頻率較低 (低于50 Hz)，屬于低頻范疇(劉紅彪等，2011a，b)，振動臺臺面的固有頻率一般為試件固有頻率的3倍以上，臺面的耦合作用對試件動力響應的影響可以忽略，故在民用建筑正弦掃頻振動臺試驗中不分析臺面耦合效應。

2.1 典型試件概況

隨著經濟的發展和人工成本的增加，鋼結構由于自重輕、工業加工自動化程度高、結構抗震性能優越等特點被廣泛應用于超高層建筑、大跨空間結構等領域 (何敏娟等，2010;黃思凝等，2012)。為了設計五層鋼框架結構的正弦掃頻振動臺試驗，先進行該結構的虛擬設計。該五層鋼框架的長和寬分別為800 mm和600 mm，一、二層層高為450 mm，三至五層層高均為390 mm，各層樓板為厚度25 mm的鋼板。模型的立面圖、細部圖和現場照片圖如圖1所示。

為了了解鋼框架結構的動力特征，分別進行了結構的模態仿真分析和模態測試試驗。模態測試試驗設備采用941B測振儀的加速度檔，靈敏度為3.10 V/g;試驗中使用初速度法對模型實施激勵，可以激起模型結構的高階振動 (劉紅彪等，2011a，b)。通過數據采集器獲取結構振動的時域數據，采用頻域分析方法對時域數據處理分析獲取了結構橫向的五階固有頻率 (表1)。根據該五層鋼框架的相關參數，采用Abaqus有限元建模計算，獲取了鋼框架結構的模態信息，其中，鋼框架結構的橫向的五階固有頻率值詳見表1，結構的前五階振型如圖2所示。通過實測數據和數值模擬結果對比可知，數值計算的固有頻率值與實測結果較接近，由此證明該有限元模型是合理的，該模型為后續結構的正弦掃頻振動臺的虛擬實現奠定了良好的基礎。

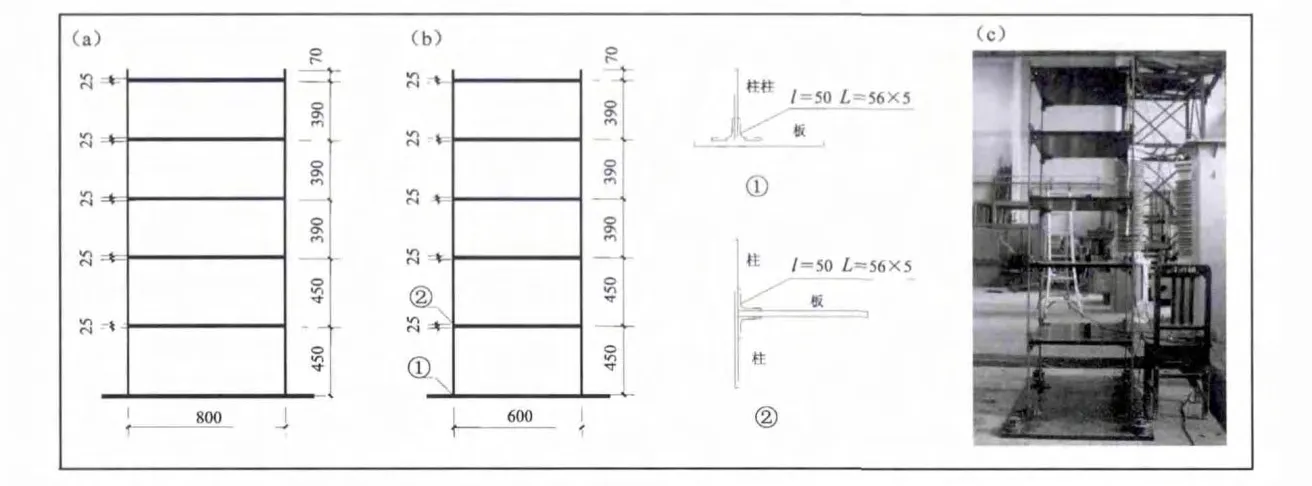
圖1 模型立面圖 (a)、細部圖 (b)和現場照片 (c)Fig.1 Elevation(a)，angle iron details(b)and locale photo(c)of the model

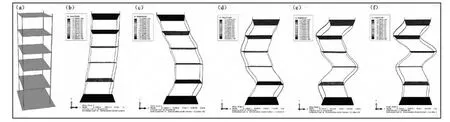
圖2 模型結構的模態(a)模型;(b)一階;(c)二階;(d)三階;(e)四階;(f)五階Fig.2 Modal of model structure(a)model;(b)first order;(c)second order;(d)thind arder;(e)forth order;(f)fifth order

表1 結構橫向的固有頻率值Tab.1 Natural frequencies of model structucre in transverse

2.2 結構的正弦掃頻仿真分析

正弦掃頻試驗是檢驗產品可靠性，解決各種結構振動問題的重要手段，尤其是在航空產品的研制過程中，正弦掃頻試驗相對于隨機振動試驗、沖擊試驗、離心加速度試驗是最能反映產品可靠性的技術指標。在土木工程領域中，正弦掃頻試驗一般用于結構的模態參數識別，尤其對結構的阻尼比測量較為有效。虛擬實現結構的正弦掃頻振動臺試驗對了解結構的動力特性，指導實際試驗合理選擇地震波的類型及量級均具有重要意義。

根據五層鋼框架結構的動力特征，在臺面底部輸入1～32 Hz的正弦掃頻激勵，設定結構的各階阻尼比為5%，通過Abaqus有限元軟件采用振型疊加法進行組合體結構的動力時程反應分析計算。正弦掃頻激勵持時 60 s，掃描速率為5.0 oct/min，分為正向和反向分別輸入計算分析，其中正向輸入的正弦掃頻時程曲線及其傅里葉譜詳見圖3，頻率隨時間變化的曲線如圖3c所示。

正弦掃頻激勵的最大峰值加速度為1.0 g，經過有限元建模計算獲取了鋼框架結構的動力響應，其中正向和反向掃頻時結構的動力響應曲線詳見圖4。從曲線上看，正反向掃頻時結構的反應趨勢是一致的，結構的最大反應發生在一階固有頻率處，最大加速度發生在結構的五層，和相關理論相符合。

為了對比正反向掃頻對結構動力響應的影響，取結構第五層的響應結果進行對比 (圖5)。經比對可知，正向正弦掃頻時，試件的最大反應發生在3.385 Hz處，五層的最大反應的加速度值為11.12 g(圖5a)，放大倍數為11.12;反向掃頻時最大反應發生在2.920 Hz處，五層的最大反應加速度值為10.23 g(圖5b)，放大倍數為10.23。可見正反向正弦掃頻時，試件的最大反應發生的頻率值存在一定差異，但差異很小，這種情況在實際的正弦掃頻振動臺試驗時也同樣存在，但對試驗的結果影響不大;同時，根據結構的放大倍數為2倍阻尼比的倒數可知，結構的放大倍數結果是合理的。

圖3 正弦掃頻曲線及其傅里葉譜(a)時程曲線;(b)傅里葉譜;(c)頻率變化曲線Fig.3 Sine sweep vibration curve and its Fourier spectrum(a)time history curve;(b)Fourier spectrum;(c)frequency varying curve

圖4 正弦掃頻下的結構動力響應(a)結構動力響應時程曲線 (正向掃頻);(b)結構動力響應頻域曲線 (正向掃頻);(c)結構動力響應時程曲線(反向掃頻);(d)結構動力響應頻域曲線 (反向掃頻)Fig.4 Structural dynamic response excited by sine sweep vibration(a)time history curve of structural dynamic response(forward sweep);(b)structural dynamic response curve in frequency domain(forward sweep);(c)time history curve of structural dynamic response(reverse sweep);(d)structural dynamic response curve in frequency domain(reverse sweep)

圖5 正反向正弦掃頻下的結構動力響應對比(a)結構動力反應曲線;(b)局部曲線Fig.5 Comparision of structural dynamic response excited by forward and reverse sine sweep vibration(a)structural dynamic response curve in frequency domain;(b)local curve

3 結論

本文通過正弦掃頻函數的理論推導和典型鋼框架結構在正弦掃頻激勵下的時程計算分析，得到如下結論:

(1)通過理論推導，獲得了正弦掃頻函數的精確描述，可為土木、機械及航空領域結構的正弦掃頻振動臺試驗的設計及動力時程數值仿真提供理論依據。

(2)結構正弦掃頻振動臺試驗時，應根據振動臺面的動力特性確定是否考慮振動臺的耦合作用對試驗件動力響應的影響;根據仿真分析可知，結構在正反向正弦掃頻激勵下的動力響應存在頻率點上的微小差異，但差異不大，兩個方向上的動力結果均可作為試件力學性能的評定指標;同時，采用振型疊加法的動力時程分析方法計算結構在正弦掃頻激勵下的動力響應是可行的，且計算速度較快。

何敏娟，梁峰，馬人樂.2010.大型超高鋼結構電視塔模擬地震振動臺試驗研究［J］．振動與沖擊，29(1):77－80.

黃思凝，郭迅，劉紅彪.2012.高層鋼筋混凝土斜交網格結構振動臺試驗研究［J］．振動與沖擊，31(11):127－132.

劉紅彪，郭迅，李國東.2011a.樂音準則法及其在結構損傷診斷中的應用研究［J］．振動與沖擊，30(10):254－259.

劉紅彪，郭迅，梁永朵，等.2011b.9度設防區房屋結構自振周期測試［J］．建筑結構，41(5):60 －62.

劉紅彪，郭迅.2012.極震區典型砌體結構的振動臺倒塌對比試驗分析［J］．土木工程學報，31(6):18－28.

劉紅彪.2012.底商多層砌體結構倒塌機理研究［D］．哈爾濱:中國地震局工程力學研究所.

田光明.2005.正弦掃描振動響應的時頻分析［J］．振動與沖擊，24(6):13－16.

楊志東，叢大成，韓俊偉，等.2008.基于擴展型準牛頓優化算法的單軸正弦掃頻控制［J］．振動與沖擊，27(3):99－103.

楊志勇，唐勝利.2006.汽輪機扭葉片的虛擬設計［J］．重慶大學學報(自然科學版)，29(1):26－29.

周寶峰，于海英，溫瑞智，等.2013.一種識別永久位移的新方法［J］．土木工程學報，46(增刊2):135－140.