定向鉆軌跡設計算法

覃 江 李銀銀 龔小霞

（長江大學機械工程學院，湖北 荊州 434023）

0 引言

定向鉆一般多用于石油、天然氣以及一些市政管道建設，由大型的定向鉆機進行鉆孔、擴孔、清孔等過程以后再進行管道回拖。在石油工業中，定向鉆技術應用較為廣泛，由于其特殊的工程性質，往往需要較大噸位的鉆機。由于地層條件的復雜多變，因此不同地層施工方案多樣化，從而造成施工的難度較大。在石油天然氣領域中，工程往往相對龐大，故而施工精度要求較高，因此對軌跡的初期設計就成減少施工問題提高工程質量的必不可少的環節。在初期的地質調研完成后，軌跡的設計對于避開不良底層以及避開障礙物方面起到了重要作用。對于軌跡設計國內外學者做了大量研究[1]，建立的軌跡設計的整體模型，對于指導工程施工具有一定的意義。然而，由于水平段的軌跡設計過于簡單，無法滿足工程實際的施工需求，故而需要進行水平段的多曲線設計。目前導向孔的軌跡設計主要是借助于CAD 等專業圖形軟件進行設計，優點是功能豐富標示清晰。然而，對于特殊需求，例如需要對設計軌跡進行鉆柱校核計算[2]時，需要開發獨立的計算軟件，因而需要一種模擬設計軌跡的算法。現有的軌跡設計軟件水平段過于簡單，無法滿足多曲線段設計。

本文在現有的設計軌跡方法[3]的基礎上，開發了水平段多曲線段的設計算法——HMCA(Horizontal Multiply Curve Algorithm)，可以適用于非開發水平定向鉆的水平段軌跡設計，以及石油鉆采領域的水平井軌跡設計。

1 水平段多曲線計算模型參

假設：

1）每個曲線均為標準圓弧；

2）沿著曲線方向，x 坐標值呈遞增趨勢；

3）曲線僅由直線和圓弧組成。

1.1 模型描述

取水平段作為研究對象，在給定水平段起點、水平段終點的情況下，對水平段進行多曲線設計。基于以上前提，多曲線的設計既簡化為一個已知圓弧半徑和起點及終點求曲線的幾何問題。當分別求出各段曲線后，用直線連接，即完成了水平段多曲線設計。

據以上分析可知，在建立整條曲線時，存在局部曲線和整體曲線的現象，為了便于幾何表達，需要建立局部坐標系和整體坐標系。

1.2 坐標轉換

在二維平面建立大地坐標系xOy，其坐標為（xi，yi），同時建立局部坐標系x`Oy`，其坐標為（xii，yii）。根據幾何坐標轉換可知[4]：

其中，x1，y1為局部坐標的原點；t 為局部坐標系按逆時針方向轉動到大地坐標系的轉角。

1.3 曲線設計

令每個曲線段的起點為（x1，y1），終點為(x2，y2)。將曲線段的起點設置為局部坐標系的原點，并將曲線按照圓心角等分成若干份。

其中β 為點線夾角；α 為弦切角；λ 為由起點和終點縱坐標的大小關系確定的控制參數；Li為第i 分微弧段對于的弦長。

關于λ 的確定方法：

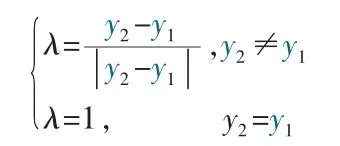
當計算完成后，按照坐標轉換，計算點在大地坐標系下的坐標值。

2 算法設計——HMCA

根據以上計算模型，設計HMCA 如下：

第一步、計算關鍵點。計算多曲線各段的關鍵點，包括起點和終點，并輸入曲率半徑；

第二步、分段計算各曲線段。計算出各個曲線段的離散點；

第三步、連接各個曲線段形成整段軌跡；

第四步、驗證相切性。在圓弧與直線的過渡段，驗證其是否相切。

3 結論

該算法能夠實現軌跡的多曲線設計，適用于水平定向鉆以及水平井軌跡設計。算法可用于開發定向鉆參數化軌跡設計軟件，邏輯簡單，便于編程實現。同時，能夠給出軌跡的離散點，可以控制離散點的距離，從而便于力學計算時的節點劃分。

［1］姚寧平，張杰，等.煤礦井下定向鉆孔軌跡設計與控制技術[J].煤炭科學技術，2013，41(3)：7-11.

［2］丁鵬，閆相禎，楊秀娟.水平定向鉆管道穿越力學參數研究[J].2007，29(5)：152-155.

［3］范培焰.定向穿越曲線優化研究[J].非開挖技術，2006，23(4)：8-10.

［4］包歡，付子傲，陳剛.基于非線性平差模型的坐標轉換公式[J].2004，21(3)：175-177.