一種基于翻轉角度的二進制粒子群優化算法

豆增發

(中國電子科技集團 第二十研究所，陜西 西安710068)

0 引言

近年來，基于仿生學的粒子群優化算法得到了飛速發展，各種粒子群優化算法被開發出來，并將其應用到了實踐當中，取得了良好的效果。二進制粒子群算法是粒子群優化算法的一種，該算法在特征選擇等方面得到了很好的應用，但是，傳統的二進制粒子群算法存在收斂速度慢和收斂值不穩定的問題，因此，為了提高二進制粒子群優化收斂速度和收斂效果，本文提出了基于翻轉角度的二進制粒子群優化算法。

1 傳統二進制粒子群優化

二進制粒子群優化的所有的粒子在一個二值搜索空間尋找最佳解。根據粒子群優化的社會方法，一個粒子決定‘是’或者‘否’的概率可以建模如下：

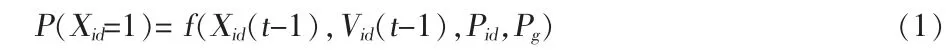
概率P（Xid=1）完全依賴于Pid和Pg。Pid是迄今為止發現的個體最佳狀態，如果最佳個體發生在Xid為1時，Pid為1，否則，Pid為0。Pg是全局最佳，如果全局最佳發生在Xid為1時，Pg為1，否則，Pg為0。Vid決定了概率函數P（Xid=1）上的一個門限值，因而其取值范圍為[0.0,1.0],可以用反曲線函數表示：

在時刻t，第i個個體在字符串中第d個位置上的狀態Xid(t)表示為：

當ρid＜S(Vid)時，Xid(t)=1;當ρid＞=S(Vid)時，Xid(t)=0。

ρid是一個在[0.0,1.0]之間均勻分布的隨機數。Vid如下式所示：

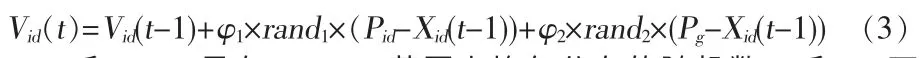
rand1和rand2是在[0.0,1.0]范圍上均勻分布的隨機數,φ1和φ2兩個參數的和為4.0。Vid的最大門限值Vmax被設為4.0。新的粒子位置由下式決定：

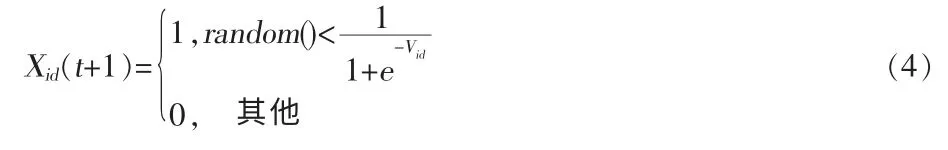
2 改進二進制粒子群優化算法

在二進制粒子群優化中，每個粒子有兩種狀態，即狀態1和狀態0，表示粒子處于狀態0的概率，表示粒子處于狀態1的概率，二進制粒子群并不是在一個連續的多維空間搜索，它實際上只是狀態的反轉而已，因此，通過對速率更新公式進行改進，移除隨機權重φ1和φ2，增加了一個狀態翻轉因子。第i個粒子的下式取0或1：位置向量根據概率進行更新，即，第i個粒子的第j個元素根據

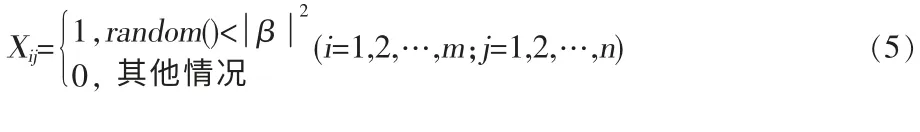
其中，random()是取值在[0,1]區間同一分布的隨機函數，m是粒子群的最大個數，n是粒子群的維度。其中， β2可以用一個翻轉速率Δθ來代替：

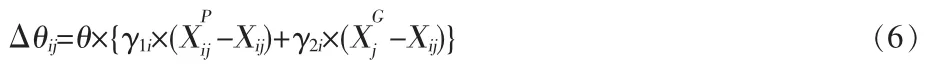
上式中，XP表示局部最優解，XG表示全局最優解，θ是翻轉角度，γ1i和γ2i是局部翻轉因子和全局翻轉因子，它們可以通過分別與局部最佳解Pbesti和全局最佳解Gbest位置的適應函數作比較獲得：

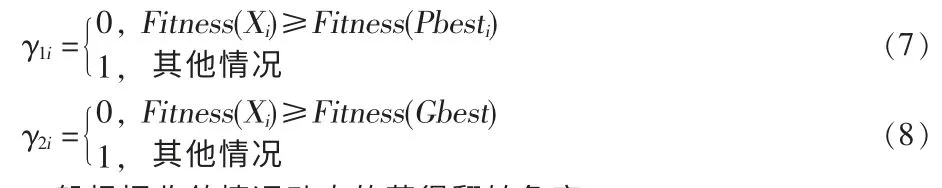
一般根據收斂情況動態的獲得翻轉角度：

上式中，θmax為最大翻轉角度，一般取0.05π，θmin為最小翻轉角度，一般取0.001π，t為當前迭代次數，M為最大迭代次數。

3 實驗結果及分析

本文將改進二進制粒子群優化和傳統二進制粒子群優化、傳統粒子群優化算法、GA算法做了比較。傳統粒子群優化的維度取30,每個算法各運行50次，然后得出平均迭代次數和平均收斂值。為了公平起見，根據經驗，二進制粒子群優化、傳統二進制粒子群優化以及傳統粒子群優化中慣性因子和學習因子都去固定參數值，即慣性因子為0.9，局部學習因子和全局學習因子為2。

本文用平均收斂速度和平均收斂值來評價改進二進制粒子群優化算法的收斂性能，結果如表1所示。總體來講，改進二進制粒子群優化的收斂速度較傳統二進制粒子群優化略快，平均收斂值要好很多。平均收斂速度v和平均收斂值t定義如下：

上式中m為迭代次數，n為測試次數，s為收斂值。平均收斂速度表示算法的平均在收斂之前的平均迭代次數，平均收斂值表示算法最后所取得的平均最優解（表1）。

4 小結

本文提出了基于翻轉教的改進二進制粒子群優化算法,該算法在二進制取值空間上，使粒子按翻轉角度進行隨機進化，最終得到使目標函數最大的二進制參數向量。與實值連續空間的粒子群優化不同，二進制粒子群在二進制空間取值，即每個粒子的取值為0或者為1，其進化速率根據一個翻轉角度隨機更新，這個翻轉角度參照全局最優解和局部最優解。

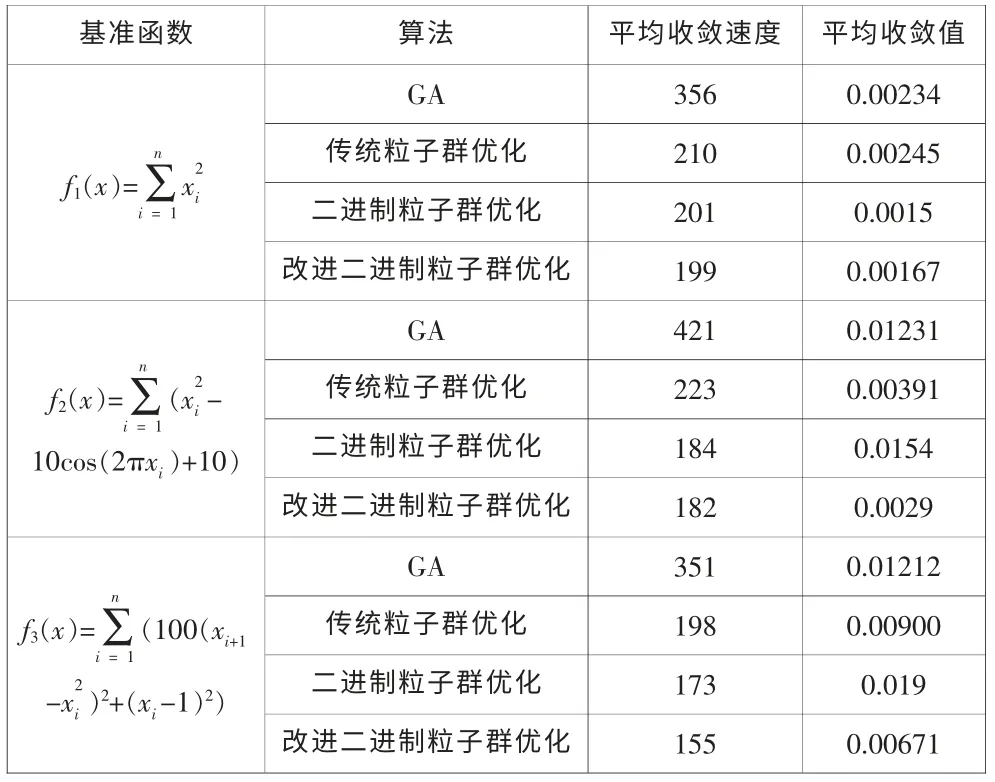
表1 改進二進制粒子群優化算法與其他算法的性能比較

［1］吳斌，史忠植.一種基于蟻群算法的TSP問題分段求解算法[J].計算機學報，2001，24（12）：1328-1333.

［2］高海兵，周馳，高亮.廣義粒子群優化模型[J].計算機學報，2005，28（12）：1980-1987.

［3］盧志剛，董玉香.基于改進二進制粒子群算法的配電網故障恢復[J].電力系統自動化，2006，30（24）：39-43.